穿梭在“一般”与“特殊”之间

姜鸿雁（特级教师）

人类认识世界，通常经历从“一般”到“特殊”，或从“特殊”到“一般”的过程，“特殊⇔一般”也是数学的重要思维方式。“平行四边形”这一章就蕴含着这一认识问题的重要方法策略。下面通过两例与同学们分享“一般”与“特殊”之间的微妙关系。

一、从一般到特殊

例1 如图1，以△ABC的三边为边在BC的同侧分别作三个等边三角形，即△ABD，△BCE，△ACF。

（1）求证：四边形ADEF是平行四边形；

（2）当△ABC满足什么条件时，四边形ADEF是矩形；

（3）当△ABC满足什么条件时，四边形ADEF是菱形；

（4）当△ABC满足什么条件时，四边形ADEF是正方形。

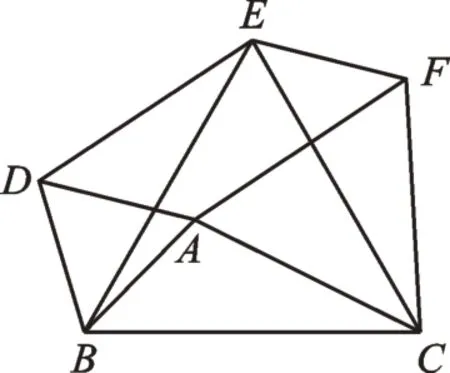
图1

【分析】由等边三角形容易得到△ABC≌△DBE，根据全等三角形对应边相等和等边三角形的性质，结合“两组对边分别相等的四边形是平行四边形”可以解决第（1）问；由此，只要四边形ADEF存在，则这个四边形一定是平行四边形，所以若为矩形、菱形或正方形，分别是从“角”“边”或“边、角”双管齐下逐步特殊化，这个特殊化的过程是通过△ABC的边和角具有特殊数量关系体现出来的。例如：若要▱ADEF为矩形，只需一个角是直角，此“重任”落在∠DAF的“身上”，结合周角360°与等边三角形每个角是60°，可知∠BAC=150°符合题意。再如，若要▱ADEF为菱形，则一组邻边（AD、AF）相等即可，“转移”到△ABC中，则为AB=AC，不过需要友情提醒的是：以▱ADEF存在为前提哦！正方形则是矩形、菱形的结合。

【简解】（1）由△ABD、△EBC是等边三角形，易得△ABC≌△DBE，则DE=AC。又AC=AF，所以DE=AF，同理DA=EF，所以四边形ADEF是平行四边形。

（2）当∠BAC=150°时，四边形ADEF是矩形。理由：由△ABD、△FAC是等边三角形可得∠BAD=∠FAC=60°，要 使 得∠FAD=90°，则∠BAC=150°。

（3）当AB=AC且∠BAC≠60°时，四边形ADEF是菱形。理由：由∠BAD=∠FAC=60°，∠BAC≠60°，所以D、A、F不共线，所以▱ADEF一定存在；由△ABD、△AFC是等边三角形可得AD=AB，AC=AF，因为AB=AC，所以AD=AF，所以▱ADEF是菱形。

（4）当AB=AC且∠BAC=150°时，四边形ADEF是正方形；结合（2）（3）易证结论，理由略。

【归纳】从“四边形→平行四边形→矩形、菱形→正方形”的认识过程，是从“一般”到“特殊”到“更特殊”的过程，所以在图形的判定过程中，“要求”越来越高，由本题我们可以窥见一斑。而在图形的性质方面，从“一般”到“特殊”的过程中，特殊的图形不仅具有一般图形都具备的共性，还具备自身独特的“特性”。从图形的对称性、边、角、对角线四个方面，随着“四边形→平行四边形→矩形、菱形→正方形”的演变历程，性质越来越多，同学们牢牢把握这条“线索”，有助于对性质的理解与掌握，在解决问题的过程中也能逐渐得心应手。

二、从特殊到一般

例2如图2，菱形ABCD的对角线AC、BD相交于点O，AC=3，BD=4，求菱形ABCD的面积。

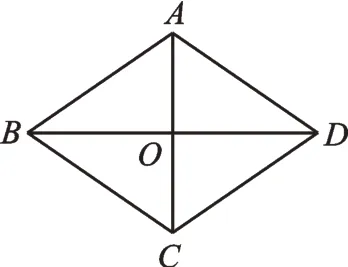
图2

【分析】菱形ABCD的面积可以看成△ABD和△BCD的面积之和。因为菱形的对角线互相垂直，经过适当变形，它的面积就是对角线乘积的一半。

【简解】因为四边形ABCD是菱形，则AC⊥BD，所以S菱形ABCD=S△ABD+S△BCD=4=6。

【归纳】因菱形的对角线互相垂直这一性质，使菱形的面积计算方法除了有平行四边形的面积计算方法（边与高的乘积），还有对角线乘积的一半，这恰好体现了前面所说的从“一般”到“特殊”的过程。细细想来，菱形的对角线互相垂直“带来”的特殊的面积计算方法，对于一切对角线互相垂直的四边形都成立。如图3，四边形ABCD，对角线AC⊥BD于点O，同例2推理过程不难得到：S四边形ABCD=CO·BD=由此，对于对角线互相垂直的四边形来说，这一面积计算方法具有通性，这正体现了从“特殊”到“一般”的过程。特别提醒：正方形的面积计算方法除了边长的平方，还有对角线平方的一半哦。

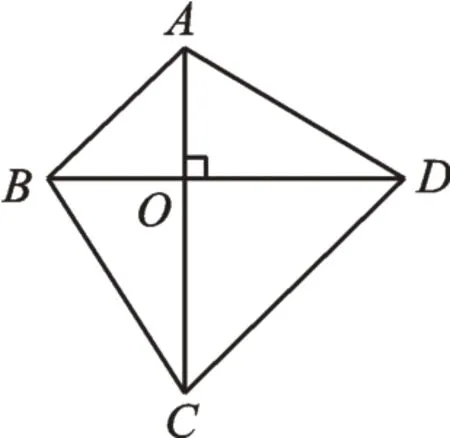
图3

学习数学的过程是基于理解的过程，是对问题的认识不断深入的过程。同学们在学习的过程中，既要学会“瞻前”，还要知道“顾后”，逐步形成整体的知识体系，利用好“一般”与“特殊”之间的辩证关系，这有助于我们对问题的认识越来越深刻。