磁电阻率法二维有限元数值模拟
尤 淼,张金会,解建建
(安徽省勘查技术院,安徽 合肥 230031)
磁电阻率法(Magnetometric resistivity method,MMR)是通过测量两点间由人工直流电场激发的磁场的勘探方法。主要研究人工传导电流和电化学作用引起的极化电流在空间各点产生测磁场变化规律,达到找矿目的。数值计算方面,邓靖武[1](2005)使用三维有限差分法研究了磁电法正演理论;杨从涛[2](2010)使用二维有限单元法进行了磁电法的数值计算。
为了解磁电阻率法的特点和异常体的响应曲线特征,使用基于矩形网格的有限单元法进行二维磁电法数值模拟并进行模型计算。
1 基本原理
稳定电流场满足的Maxwell方程组为:

存在本构方程:
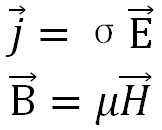
σ为电导率,μ为真空磁导率。
由Maxwell方程组和本构方程可以看出,要获得磁场强度H,需首先计算电场强度E。由于电场E是矢量场,引入标量电位u,令电场E表示为标量电位u的梯度形式:

使用有限单元法计算点电流源在研究区域引起的标量电位u,在利用上式,可计算电场强度E,进而求出稳定电流场激发出的磁场强度H。
2 点源二维地电断面的正演问题
假设在地表A处,存在一电流源I,电流密度矢量为 。研究区域Ω为二维地电断面,与构造走向垂直,边界为Γ,如图1。

图1 二维电场示意图
满足如下关系:

根据奥斯特-高斯公式,有:

δ函数满足积分关系:

因此有如下关系:

因为电位u与电流密度矢量的关系为:

σ为介质的电导率,整理上式,可得电位满足的微分方程:

考虑地面Γs上的电流,因空气中电阻率可视为无穷大,所以流向空气中的电流密度为0,即电流密度在地面上的法向分量为0,因此电位的法向导数为0:

在无穷远边界Γ∞上,可假设研究区域的不均匀性对边界上的电位没有影响,其表达式为:

其中,c是比例系数,r"是点源到该边界点的距离。有限元求解区域需足够大,以满足此边界条件。
因研究区域为三维场源、二维构造,对于此类边值问题,需要进行傅里叶变换,变换到二维波数域中进行求解,经过傅里叶变换后的二维边值问题为:

其中,σ为电导率,k为波数域中的参数,U是波数域中的电位,I是供电电流,δ(A)是供电点的位置,为波数域中电位对地表边界的外法向。K0为第二类零阶修正贝塞尔函数,K1为第二类一阶修正贝塞尔函数,cos(r,n)为边界上A点到该边界点的矢径r与该点外法向n之间夹角的余弦。点源二维电场的内边界条件是自然边界条件,在泛函极值过程中将自动满足。
使用加权余量法,得到点源二维电场的变分问题为:
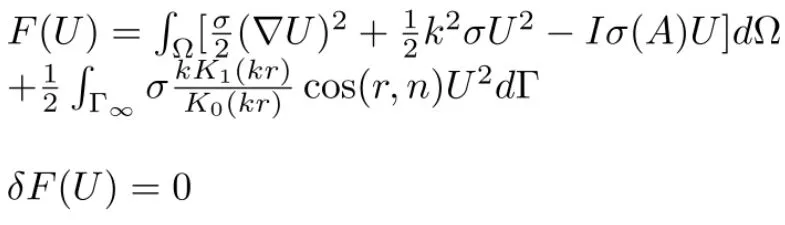
3 网格剖分
研究区域采用如下图所示的矩形网格剖分,有限单元法采用矩形单元,双线性插值,在区域中心进行网格加密处理,边界处网格稀疏化。

图2 矩形网格剖分示意图
4 总体集成
将区域积分分解为各矩形单元上的积分,根据叠加原理,扩展成全体节点组成的线性方程组:

KU=P
有限单元法计算中,刚度矩阵K采用变带宽存储,以节约计算机内存空间。使用Cholesky分解法求解上式的方程组,获得波数域k中各节点的电位值U。
5 傅里叶反变换
对于每个节点,由不同波数k计算出一组U,再使用傅立叶反变换计算出三维空间的电位u。
由于u(x,y,-z)=u(x,y,z),故采用余弦形式,数值积分方法:

采用最优化方法,选取5点波数进行傅里叶反变换[3]。
6 计算电流密度
由有限单元法计算获得各节点电位U后,根据下式计算各节点电流密度j:

在直角坐标系下展开,得到:

7 计算磁场
已知稳定电流磁场满足如下关系式:

将上式在直角坐标系下展开,得到电流密度矢量和磁场矢量的关系式:

将所有节点电流密度和磁场关系式关系整理,得到如下方程组:

其中,jx1表示1号节点在x方向的电流密度分量值,上式中,节点总数为M×N。求解上述方程组,即可得到二维研究区域内,各节点的磁场分量。
8 模型验证
网格剖分在水平方向为中间区域网格数40,水平间距1m;左右区域各12个稀疏网格,成等比例剖分。剖分区域水平方向总长度为200m。垂直方向25个网格,浅部加密剖分,深部稀疏剖分。最大深度为800m。
8.1 模型一
模型一为均匀半空间模型,电阻率为10Ω·m,水平偶极源AB,偶极中心深度为6m,偶极距4m。地表各节点磁场Hy分量如下图所示。

图3 模型一地表各节点磁场Hy分量
8.2 模型二
模型二为均匀半空间模型,电阻率为10Ω·m,垂直偶极源AB,偶极中心深度为6m,偶极距10m。地表各节点磁场Hy分量如下图所示。

图4 模型二地表各节点磁场Hy分量
8.3 模型三
模型三为二维模型,地下背景电阻率为10Ω·m,水平偶极源AB,偶极中心深度为6m,偶极距4m。在地表测线中心向下深度30m处,存在一个规模4m×4m的高阻异常,电阻率为100Ω·m。

图5 模型三剖面图
计算获得的地表各节点磁场分量如下图所示。

图6 模型三地表节点磁场Hy分量曲线图
9 结论
本文使用二维矩形网格剖分的有限单元法,计算了几个典型地电模型的磁电法响应。因采用矩形网格剖分线性插值,数值解的结果曲线不够平滑,需使用三角形等更精细的剖分方式或高阶插值方式。二维计算中,磁场所求解方程组为欠定,使用最小二乘法求解,会造成精度的损失,需考虑使用三维点源电位进行计算。

