GPS/INS超紧组合载波跟踪环路最优带宽在线设计
许萧寒,王可东
北京航空航天大学 宇航学院,北京 100191
在GPS (Global Positioning System)接收机设计中,载波锁相环(Phase Locked Loop, PLL)用来完成对接收载波信号的本地复制,并对其相位和频率进行锁定,是卫星导航接收机的关键技术。为了提高接收机对环路噪声的抑制能力,要求载波环路采用较小的噪声带宽和较长的预检测积分时间。但是,为提高接收机对载体动态的跟踪能力,又需要环路采用较大的噪声带宽和较短的预检测积分时间[1]。为解决此问题,文献[2]应用四阵元圆心阵的抗干扰算法从硬件设计角度提高了接收机的抗干扰能力;文献[3]提出了两级快速傅里叶变换多普勒频率捕获方法提高了多普勒频率估计精度;文献[1]采用锁频环(Frequency Locked Loop, FLL)辅助并采取差分相干累加比特同步算法以增强PLL环路的抗干扰性能以及对载体高动态的跟踪能力;文献[4-5]应用无迹卡尔曼滤波器、扩展卡尔曼滤波器取代传统环路中的鉴别器和低通滤波器以提高载波环路的动态跟踪性能。当前,随着惯导技术的普及,利用惯导系统(Inertial Navigation System, INS)与GPS构成组合导航系统,并通过校正后的INS提供载体动态信息与卫星星历信息计算多普勒频移,辅助接收机对GPS信号的跟踪成为了同时提高接收机抗噪能力和动态跟踪能力的有效途径。
目前对INS/GPS超紧组合导航系统的研究中,在跟踪误差建模的研究方面,文献[6]针对二阶载波跟踪环路将INS多普勒辅助误差拆分为噪声项和偏置项进行计算,并针对低动态载体推导了辅助误差计算方法。
在跟踪误差的计算方式研究中,文献[7]给出的环路跟踪误差的计算方法,文献[8]在设定动态应力上限的条件下验证了INS辅助下环路带宽的下降;在只考虑热噪声和动态应力的情况下,文献[9-10]针对固定的载噪比和载体动态情况,通过计算跟踪误差均方差对带宽偏导数等于0来求解最优带宽;文献[11]利用实时检测的信号载噪比,以载体典型动态为基准建立了载噪比与最优带宽的查找表。然而,上述方案对实时变化的载噪比和INS动态辅助残差的应用尚且比较缺乏,易出现实际动态条件偏离设计点而导致带宽的计算丧失最优性。
在最优带宽实时计算方法的研究中,文献[12-13]通过仿真数据建立了最优带宽与信号载噪比的一次、二次函数关系,结合载噪比的测量新息计算各时刻的最优带宽;文献[14]在未考虑INS辅助的情况下以热噪声和动态应力误差的能量最小为目标函数,使用离散牛顿二阶梯度法迭代解算最优带宽,然而目标函数计算复杂,需要100次迭代才能计算得到最优带宽;文献[7]基于载噪比信息将环路带宽的计算划分为2种模式,并通过固定带宽增量的方式来计算门限带宽和最优带宽,然而其收敛速度和收敛精度受到设定步长的影响,因而目前缺少能够以较小计算量实时计算最优带宽的设计方案。
针对当前研究中出现的问题,本文推导了多普勒频率估计误差及多普勒频率变化率估计误差的计算方法,针对二阶载波跟踪环路给出了INS动态估计残差的统计指标,在此基础上综合考虑热噪声、机械振动、晶振Allan方差等误差源的影响,结合实时测定的载噪比信息,应用二阶梯度法对载波跟踪环路最优带宽进行实时迭代解算,提供了一种根据载体实际运动情况实时计算环路最优带宽的方式,有助于在实际工况下提高接收机载波环路的跟踪性能。
1 INS辅助载波跟踪环路建模
INS辅助GPS接收机载波跟踪环路误差传播结构可以建模为如图1所示的控制环路。
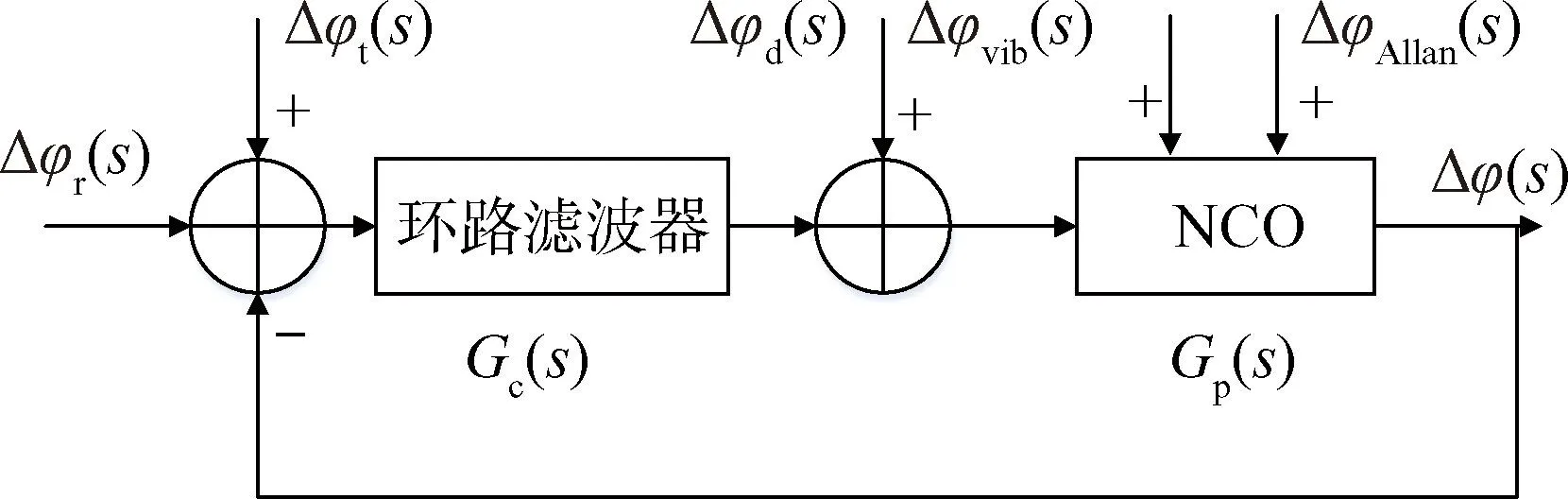
图1 载波跟踪环路误差传播Fig.1 Doppler aiding carrier tracking loop error propagation

因此相位跟踪误差可以表示为:
Δφ(s)=H(s)Δφt(s)+[1-H(s)]Δφvib(s)+
[1-H(s)]ΔφAllan(s)+Hd(s)Δφd(s) (1)
其中各部分传递函数可以表示为:
(2)
由式(2)中各误差源的传递函数可知,热噪声为宽带噪声,带宽越大其引发的跟踪误差越大;而机械振动、晶体Allan方差、多普勒辅助误差等误差源为窄带噪声,带宽越小其引发的跟踪误差越大。因此,当INS/GPS超紧耦合系统带宽降低时,需要综合考虑各类误差源的影响,进而进行最优带宽的设计。
2 载波环跟踪误差建模
PLL环路1σ跟踪误差σPLL可以表示为:
(3)
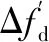
在INS辅助条件下,接收机可以得到多普勒信息的有效估计,但是其估计误差依旧需要PLL环路进行跟踪。若PLL采用二阶环路的形式,则多普勒频率估计误差将以噪声的形式影响跟踪精度,而多普勒频率变化率估计误差将以稳态误差的形式影响跟踪精度。
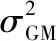
(4)
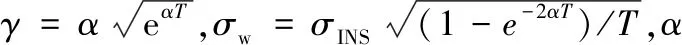
对于二阶PLL环路,由INS计算的多普勒频率变化率估计误差将造成环路的稳态跟踪误差θRR,其具体形式为:
(5)
式中:稳态跟踪误差的幅度ARR由多普勒频率变化率估计误差的精度σafd决定,即ARR≈3σafd[6]。由式(4)(5)可知,INS辅助信息的精度直接影响着PLL环路的相位跟踪精度,因此σfd,σafd的在线估计是PLL跟踪误差实时计算的必要步骤。
在INS/GPS超紧耦合系统中,通过INS输出的接收机位置、速度信息以及卫星星历信息计算多普勒频率测量值,其具体计算方式为:
(6)
式中:fd为载波信号的多普勒频率;e为视线方向向量;vR为接收机速度向量;vS为卫星速度向量;λ为载波波长。
(7)

(8)
其中符号上方的“~”均表示带有误差的值。用式(8)减去式(7),且忽略由载体位置估计误差引起的视线方向偏差,可得多普勒频率估计误差为:
(9)
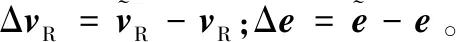
因此,多普勒频率估计误差的方差可以计算为:
(10)
在惯导递推周期中,P(ΔvR)可用一步预测协方差阵中速度误差协方差阵,在组合滤波周期中P(ΔvR)可用量测更新协方差阵中速度误差协方差进行计算。
对式(10)两边求导可得多普勒频率变化率估计误差:
(11)
式中:I为3行3列的单位矩阵。将式(12)代回式(11)可得多普勒频率变化率估计误差为:
(13)

因此多普勒频率变化率估计误差的方差可以计算为:
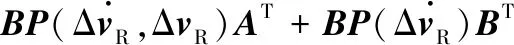
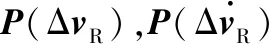
(15)
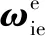
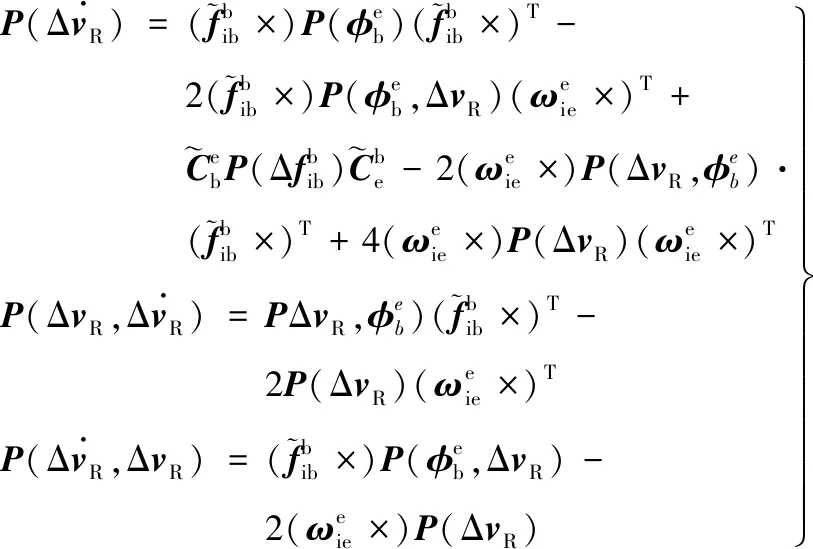
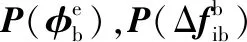
至此,结合式(4)(5)(10)(14)(16),可以实时计算由INS辅助误差引起的相位抖动和稳态跟踪误差。
3 最优带宽计算
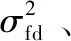
3.1 载噪比C/N0的实时测定
在接收机某一通道中,以Tcoh为相干积分时间,通过连续M组即时相干积分值Ip(n)、Qp(n)来计算第k个相关积分周期时宽带功率Pwb(k)和窄带功率Pnb(k),并计算二者的比率Pnw(k):
(17)
为降低Pnw(k)中的噪声量,先对Pnw(k)进行K组平均,进而计算载噪比:
(18)
3.2 最优带宽的实时计算

应用离散牛顿二阶梯度法,第i步迭代增量的计算方法如式下:
(19)
式中:J(xi),H(xi)为别为σPLL关于Bn的一阶导数和二阶导数在xi点的取值,在应用中采用小间隔差商代导数计算,当增量相对于当前带宽数值变化小于1%时,认为收敛稳定,停止迭代,取当前迭代结果作为最优带宽Bopt。
最优带宽的计算流程为:
1)设定初始迭代步数i=1,带宽迭代初值Bn(i)=10 Hz,离散带宽步长BnGap=0.01 Hz,精度水平ε=1%,最大迭代次数N=20。
2)通过BnGap计算Bn(i)的一阶、二阶差商代替一阶、二阶导数。
3)根据式(19)计算迭代增量。
4)若满足|Δxi|/|Bn(i)|≤ε则停止迭代,Bopt=Bn(i);否则Bn(i+1)=Bn(i)+Δxi。
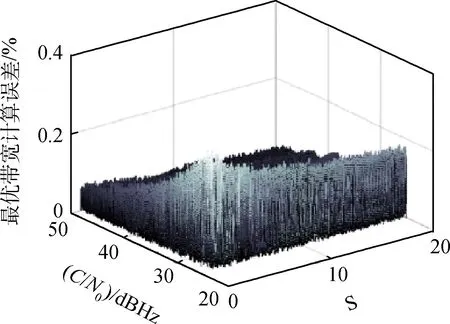
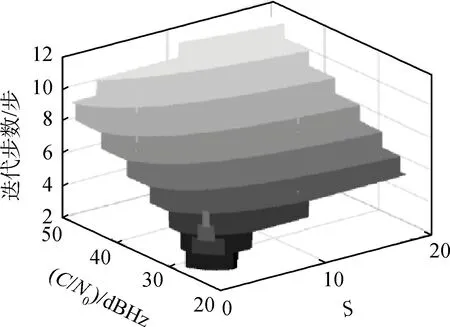
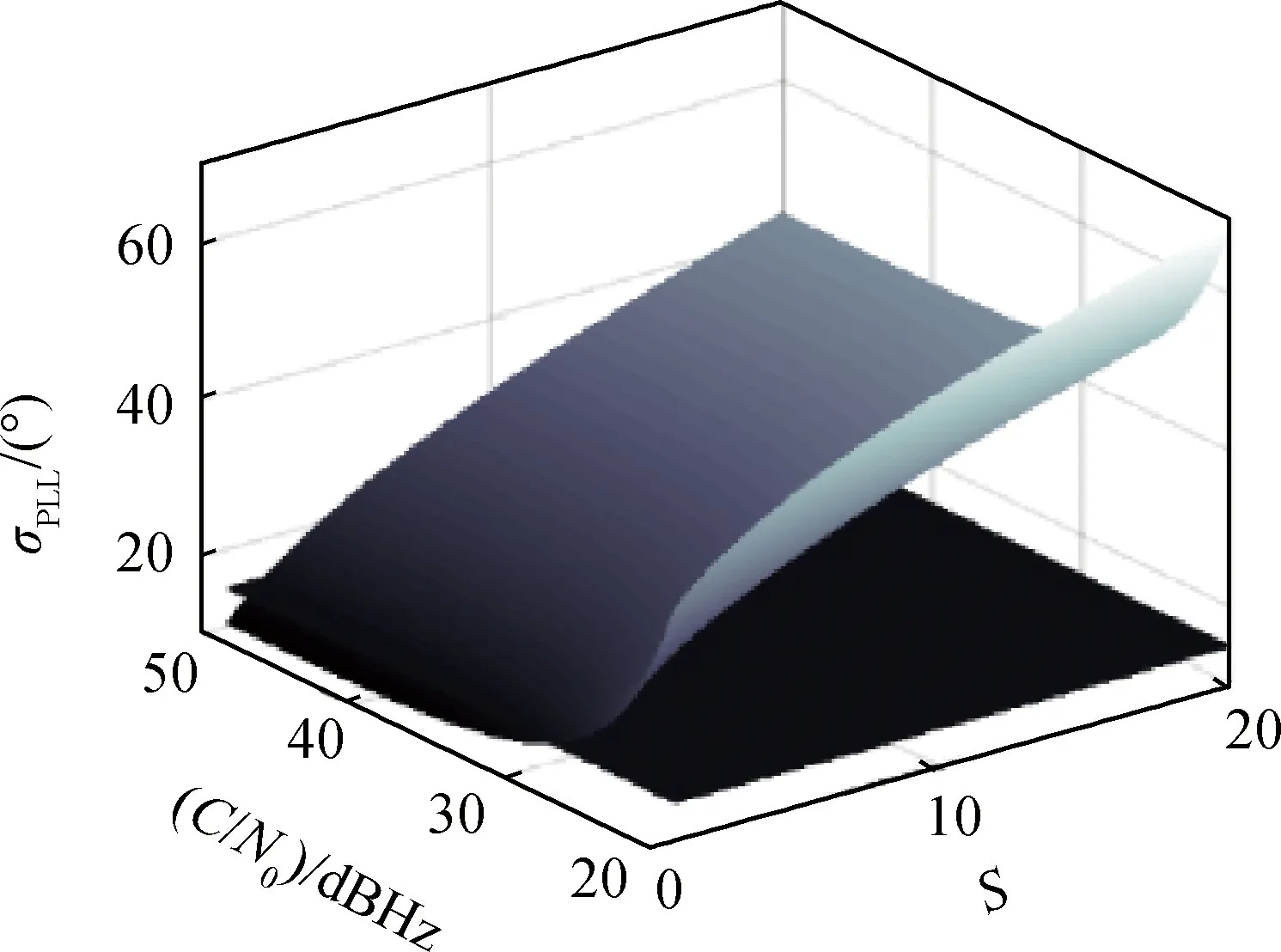
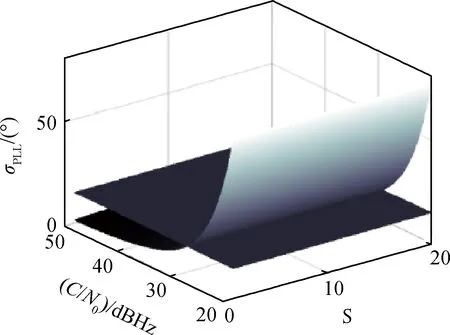
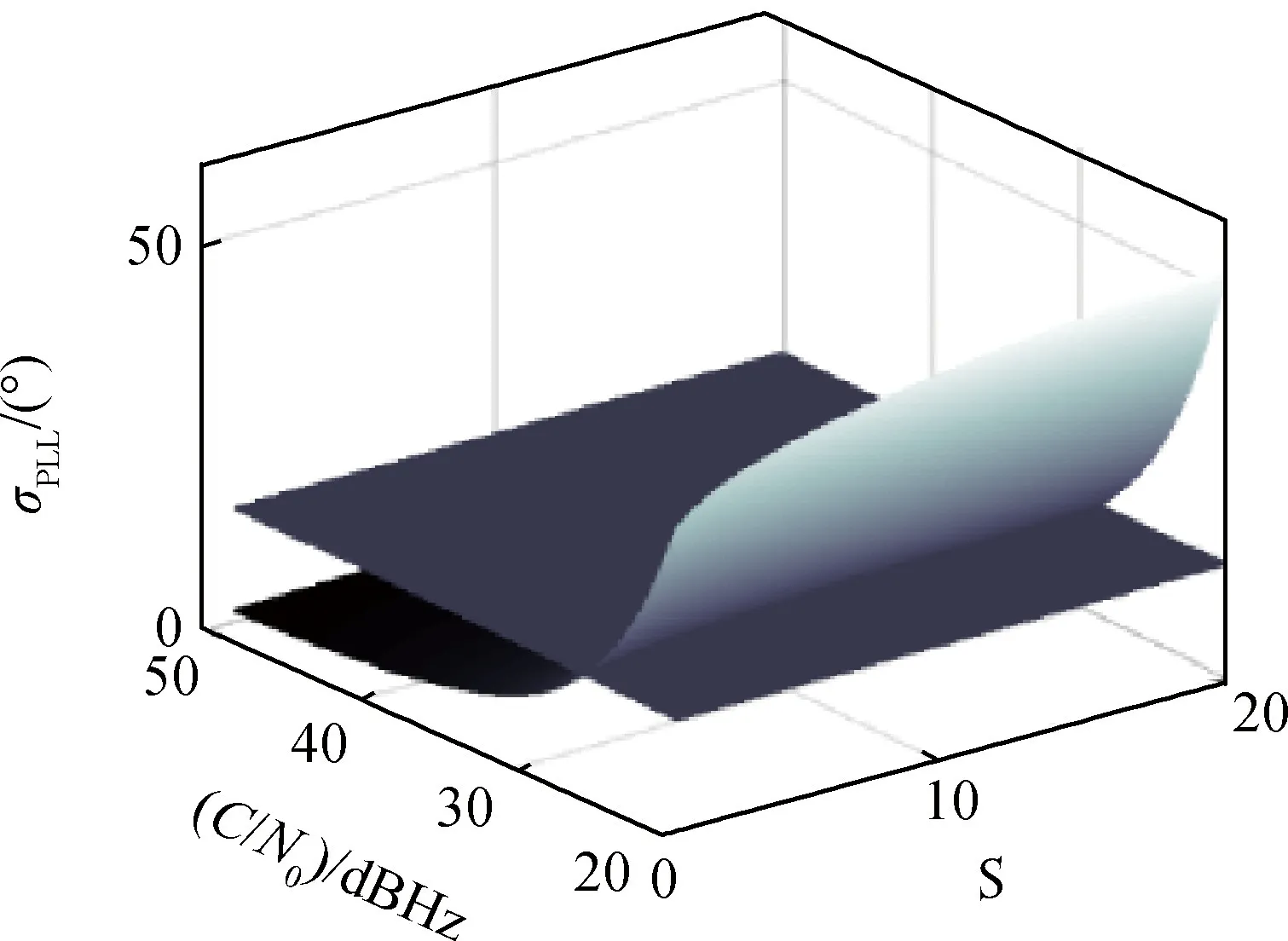
5)迭代步数i增加1,若i 以车载载体为研究对象,设载体的位置为东经116.343 4°、北纬39.979 8°、高度39 m,以40 m/s的速度向北行驶,取卫星的位置为载体正上方,即东经116.343 4°、北纬39.979 8°,高度为GPS卫星平均轨道高度20 200 km,以 3 804 m/s的速度向北运行。接收机OCXO晶振、卫星Ce原子钟的时钟模型按照文献[8]进行设置,相应时钟参数取文献[8]中的典型值。 误差协方差阵设置如下: (20) 载体本体坐标系加速度信息和ECEF坐标系地球自转角速度信息如设置: (21) (22) (23) 图2显示了在不同实现距离、载体速度的情况下,由式(22)引起的计算偏差。 图2 文献[6]中的方差计算偏差Fig.2 Deviation error of algorithm in reference [6] (24) 应用迭代的方法计算最优带宽,图3、图4分别显示了迭代结果与最优带宽理论值的偏差百分比以及迭代所用的步数。从图3中可以看到,在不同载噪比和辅助误差条件下,迭代方法的计算误差始终保持在0.4%以下。同时图4显示,在各类条件下,迭代步数保持在11步以下,在保证计算精度的同时,相比于文献[12]中100次的迭代次数大幅提高了实时性。 将固定带宽下的跟踪误差σPLL(Fixed Bn)与最优带宽下的跟踪误差σPLL(Optimal Bn)的偏差记为ΔσPLL: ΔσPLL=σPLL(Fixed Bn)-σPLL(Optimal Bn)(25) 图3 迭代算法计算误差Fig.3 Calculation error of iterative algorithm 图4 迭代步数Fig.4 Iterative steps 分别以5Hz、30Hz固定带宽以及以实时最优带宽作为环路带宽,图5~图9显示了在不同载噪比、不同辅助误差条件下环路跟踪效果,以及不同带宽情况下跟踪误差的对比。 图5 5 Hz固定带宽环路跟踪误差门限Fig.5 Error threshold of 5 Hz bandwidth tracking loop 图6 5 Hz固定带宽环路与最优带宽环路跟踪误差对比Fig.6 Difference of 5 Hz bandwidth loop and optimal bandwidth loop tracking error 图7 30 Hz固定带宽环路跟踪误差门限Fig.7 Error threshold of 30 Hz bandwidth tracking loop 图8 30 Hz固定带宽环路与最优带宽环路跟踪误差对比Fig.8 Difference of 30 Hz bandwidth loop and optimal bandwidth loop tracking error 从图5可以看到,在辅助误差较低时,应用5 Hz固定带宽的环路对弱信号情况有相对较好的跟踪性能,但是随着辅助误差增加,低固定带宽的环路无法跟踪较大的动态应力残差,跟踪性能下降明显,甚至导致环路失锁。从图6可以看到,当S=1时其跟踪门限为28 dBHz,当S=20时,在各类信号强度条件下环路跟踪误差都已超过15°,环路已经失锁。 图9 实时最优带宽环路跟踪误差门限Fig.9 Error threshold of optimal bandwidth tracking loop 从图7可以看到,应用30 Hz固定带宽的环路对于辅助误差有较强的跟踪能力,且在强信号情况下有较好的跟踪精度,但当接收信号载噪比降低时,大固定带宽的环路易过多的引入热噪声,导致跟踪误差增大,从图8看到,当C/N0=50 dBHz时其与最优跟踪误差的偏差为1.3°,当C/N0=25 dBHz时其与最优跟踪误差的偏差将超过10°。 从图9可以看到,相比于固定带宽环路,应用实时最优带宽的环路在弱信号、低辅助精度情况下的跟踪能力有明显提升,当S=20时其跟踪门限为26 dBHz,同时在强信号、辅助精度较高的良好外部环境下能够进一步提高环路的跟踪精度,当C/N0=50 dBHz、S=1时其跟踪误差可降低至1.5°。 本文分析了视线方向变化率与载体速度误差等因素对多普勒频率估计误差、多普勒频率变化率估计误差造成的影响,结合组合滤波器对导航状态和惯导器件误差的精度估计,推导了二阶载波跟踪环路INS动态估计残差的统计指标,提高了高轨、高动态条件下的辅助误差描述精度指标的计算方法。在INS辅助条件下,环路带宽得以降低,窄带噪声不可忽略,最优带宽与跟踪误差构成高阶非线性关系,本文利用实时测定的载噪比信息、多普勒辅助误差信息,以最小化跟踪误差为目标,应用离散牛顿二阶梯度迭代算法,以二阶速度逼近带宽的数值最优解,在保证最优带宽计算精度的同时显著降低了迭代次数。仿真试验表明,本文设计的最优带宽迭代解算方法能够11次迭代内达到99.6%的计算精度;对比固定带宽方案,应用本文提出的最优带宽计算和调整方案能够在弱信号、辅助信息精度较低的情况下有效提高环路的跟踪精度,提高环路抗干扰能力和动态跟踪能力。4 最优带宽设计方法验证



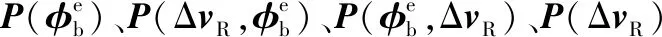


5 结束语

