基于SPEA2算法的UCAV多目标机动轨迹规划
朱文强,杨卫莉,库 硕,王 杰
(1. 空军工程大学航空工程学院,西安,710038;2. 中国人民解放军93617部队,北京,101400)
1 引 言
无人战斗机(UCAV)经过战术决策与机动决策后,急需将决策的结果转换为飞行控制系统能够识别的轨迹指令,这一过程称为UCAV 机动轨迹规划[1]。其目的是为UCAV规划出一条最优的机动轨迹,使得UCAV 能够顺利执行决策出的结果。在规划过程中,既需要考虑UCAV 飞行控制系统的控制性能,即轨迹的可跟踪性;同时也要考虑UCAV相对于敌机的态势在当前情况下最优。目前,针对各种飞行器(或UCAV)的轨迹规划问题已有不少相关文献。文献[2]综合考虑了UCAV 的动态RCS 特性与攻击时间最短的要求,采用可变低阶自适应伪谱法解得最优攻击轨迹。文献[3]针对高超声速滑翔飞行器轨迹优化问题,提出了轨迹分段优化策略,利用高斯伪谱法将连续多段最优控制问题转换为非线性规划问题进行求解。
传统的UCAV轨迹规划问题一般都是单目标问题,例如威胁代价最小、燃油消耗最小[4]、飞机操纵性最好[5]等。或者涉及到多个优化目标时,为了使问题简化,通过引入权重再求和,从而将多个性能指标函数结合成一个目标函数,将问题转化为单目标优化问题[6]。这种方法虽然使得问题简化了,但是权重因子的确定又增加了问题的复杂性,且无法评价权重因子的好坏[7]。本文提出的UCAV机动轨迹规划是一个多目标优化问题,且两个优化目标之间具有一定的冲突性,不存在某一个解能够同时使得两个目标的性能指标最优,因此只能求出一组均匀分布的Pareto 最优解集[8]。针对上述多目标优化问题的特殊性,本文采用SPEA2多目标遗传算法进行求解。
2 UCAV机动轨迹规划模型
2.1 UCAV运动模型
2.1.1 UCAV运动方程
采用UCAV 三自由度模型对UCAV 的运动状态进行描述。现做出如下假设:(1)将UCAV 视为质点,不考虑其形状;(2)忽略侧滑角;(3)忽略地球自转和曲率的影响,将地面坐标系作为惯性坐标系;(4)忽略气流与阵风的影响;(5)忽略高度与经纬度对重力加速度的影响。基于以上假设条件,可以建立如下UCAV 在惯性坐标系下的运动模型[9]:

其中x,y,z,V,γ,φ,ψ,α分别表示UCAV在惯性坐标系中x,y,z轴的坐标、速度、航迹倾角、滚转角、偏航角和迎角,δ,Tmax,L,D分别表示油门位置、发动机最大可用推力、UCAV 受到的升力、空气阻力。选取X=[x,y,z,V,γ,ψ]作为状态量,U=[δ,α,φ]作为控制量。
2.1.2 UCAV气动力模型
UCAV 受到的气动力为升力和阻力,其具体模型如下:
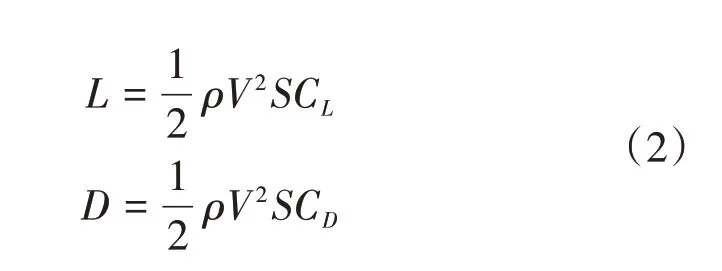
其中ρ为空气密度,其具体值随着UCAV 的高度变化,S为UCAV 的参考横截面积,CL,CD分别为升力系数和阻力系数。具体可采用F-4涡喷发动机的相关气动数据进行拟合,拟合公式如下:

2.1.3 UCAV燃料消耗模型
由于在实际飞行过程中,UCAV 的燃料不断消耗,故其质量会持续减小,通常使用以下模型来近似描述UCAV的质量变化情况:

其中c为UCAV的燃料消耗系数,c=6.377551×10-6,T为发动机实时推力。
2.1.4 UCAV发动机推力模型
由于实际发动机推力模型比较复杂,涉及到的参数众多,故在实际应用中常采用如下简化模型:
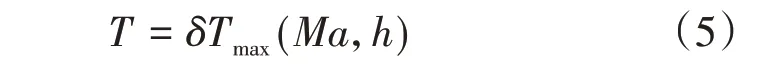
其中的发动机最大可用推力Tmax可采用F-4涡喷发动机模型:

其中Ma为UCAV 马赫数,h为UCAV 的高度z转换为以10000 英尺为单位后的高度,Tmax以1000 磅为一个单位。
2.2 空战态势评估模型
本文以超视距空战为背景,超视距空战几何态势如图1所示。V,VT分别表示UCAV与目标机的速度,D表示UCAV 与目标机的相对距离,φ表示目标机相对于UCAV 的方位角,q表示目标机进入角,θ表示目标机航向角,其中q,θ互补。

图1 空战几何态势图Fig.1 Geometric situation of air battle
由于超视距空战的最终目的是使得目标机进入我机的导弹攻击区内,并发射导弹,因此导弹攻击区对于空战态势的影响十分重要,除此之外,影响空战态势的因素还有方位角、进入角、速度、高度和距离[10]。针对这一特点,构建基于导弹攻击区的态势评估模型。
2.2.1 导弹攻击区拟合
导弹攻击区是由当前的敌我方位决定的,是在敌我连线上的一段距离,主要由近边界和远边界两个距离组成。由于导弹攻击区的实时解算计算量大且比较复杂,故在此选择一组某型三代中距空空导弹进行拟合:
(1)迎头攻击时
即当60∘≤q≤300∘时,同时满足:且V<1.8Ma时:其中Ḋ表示UCAV 与目标机距离变化率,Dmax,Dmin分别表示导弹攻击区的远边界和近边界。
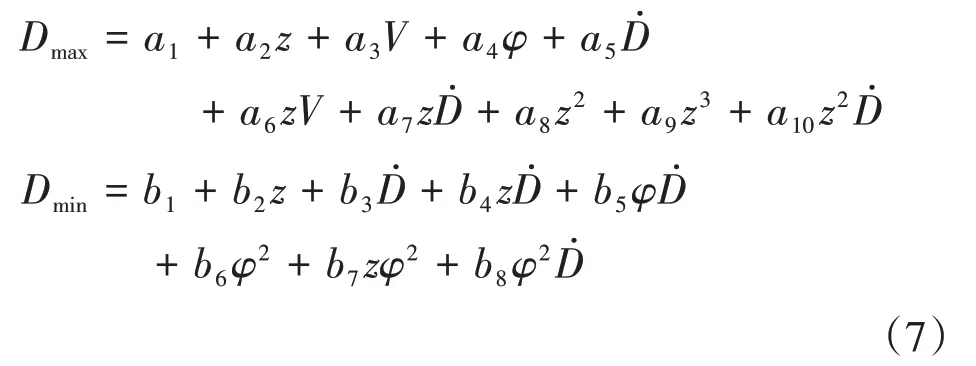
(2)尾后攻击时
即当-60∘<q<60∘时,同时满足且V<2.2Ma时:
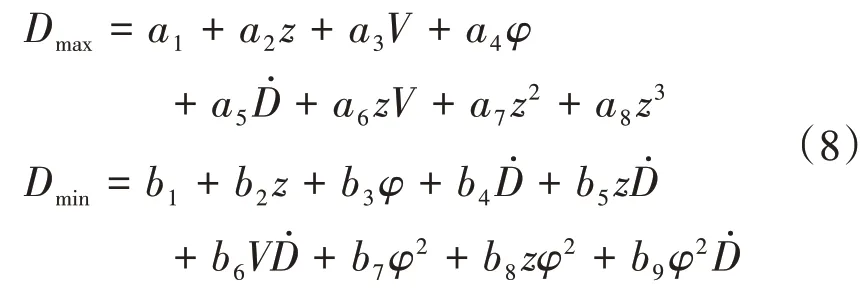
2.2.2 角度态势因子
在空战过程中,方位角和进入角对于空战态势的影响具有耦合关系,同时考虑到UCAV 的机载雷达探测性能以及预警机和地面指挥所的信息支援,可采用如下角度隶属度函数:

其中φmkmax表示不可逃逸区最大偏角,φmmax表示导弹可发射最大离轴角,φRmax表示机载雷达搜索区最大偏角。
2.2.3 速度态势因子
在空战中,速度优势对于空战态势的影响十分明显,对于同一型空空导弹而言,当载机具有更大的速度优势时,导弹相应的攻击区也更大。然而,当载机速度过大时,载机的机动能力也会相对变差。针对速度的这一特点,可以采用如下速度隶属度函数:
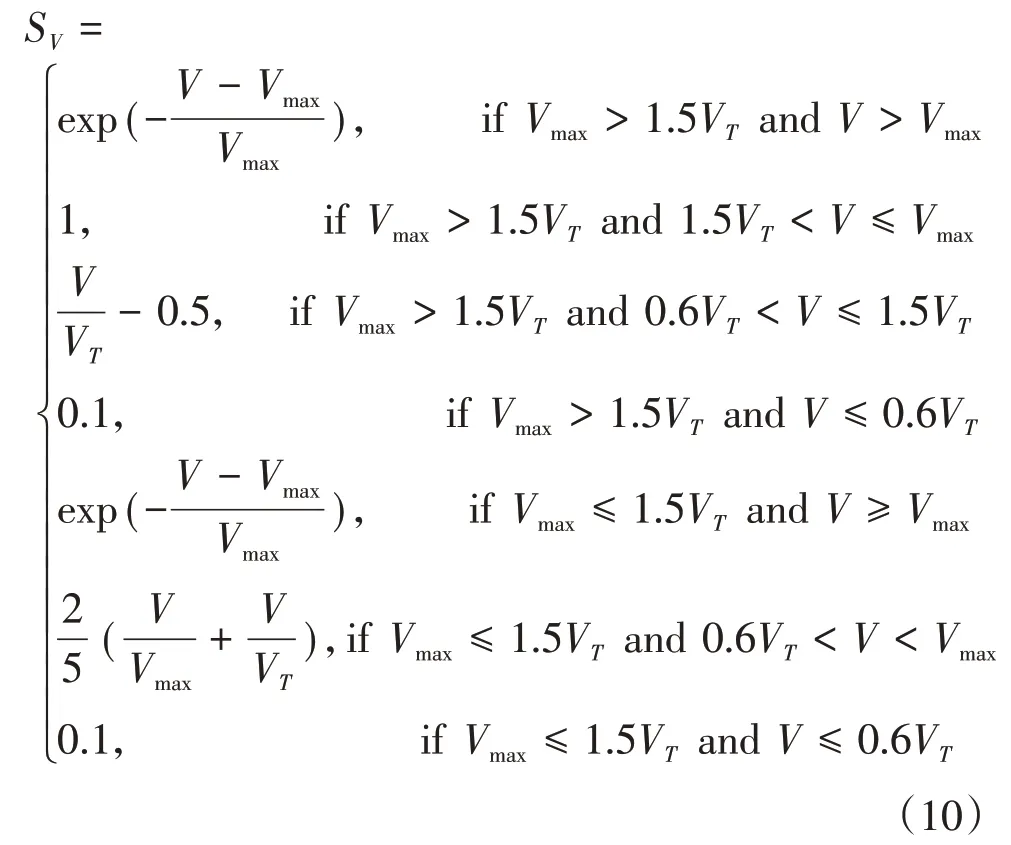
上式中Vmax表示UCAV的最佳空战速度。
2.2.4 高度态势因子
超视距空战过程中,对同一型空空导弹而言,在其他条件相同的情况下,载机的高度越高,导弹具有的势能越大,导弹对目标机的攻击区越大,因此会具备更好的空战态势。但是,当载机与目标机的高度差过大时,会影响到导弹自身的性能,因此,不是高度差越大越好。采用如下高度隶属度函数:

上式中zmax,zT分别表示UCAV最佳空战高度和目标机当前高度。
2.2.5 距离态势因子
考虑机载雷达探测距离以及导弹攻击区对于空战态势的影响后,可采用如下距离隶属度函数:
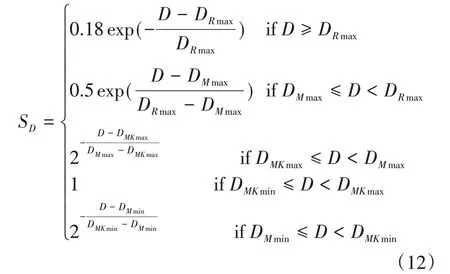
上式中DRmax,DMmax,DMmin,DMKmax,DMKmin分 别 表 示UCAV机载雷达最大探测距离、导弹攻击区远边界、导弹攻击区近边界、导弹不可逃逸区远边界和导弹不可逃逸区近边界。
2.2.6 超视距空战态势评估模型
在实际空战中,由于距离与角度具有耦合关系:当UCAV 与目标机距离较近时,角度优势对于态势的影响较大;当距离较远时,角度优势影响较小。针对这一特点,采用如下形式的态势评估模型:
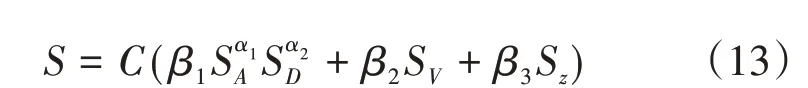
上式中权重系数满足:α1+α2= 1,β1+β2+β3= 1;C表示UCAV 的空战能力[11],决定UCAV 空战能力的因素主要有:战机生存力、探测目标能力和战机火力和外部信息支援。
2.3 UCAV机动轨迹规划模型
考虑到机动轨迹的可跟踪性以及态势的最优,其中UCAV的态势最优即等价于目标机对于UCAV的威胁最小,故优化的目标即为:

上式中J1表示轨迹的跟踪特性,即规划的轨迹以及控制量的平滑度,J1越小,则轨迹越平滑,跟踪特性越好。J2表示目标机对于UCAV 累积的威胁,J2越小,则表示UCAV 相对于目标机的态势越好。针对J1的具体表达式进行分析,在一条机动轨迹上设置n个能够表征其特征的特征点,同时针对该轨迹的特性将其划分为m条轨迹片段,设定在每一个轨迹片段内的控制量变化率是定值,即在各个轨迹片段内的控制量将均匀变化,这样将使得整条轨迹更加平滑,也将提升该轨迹的可跟踪性。上式中Pi(X)表示第i个特征点处的罚函数,用来约束轨迹的状态,Wi表示第i个特征点的权重,其中Pi(X)表达式如下:
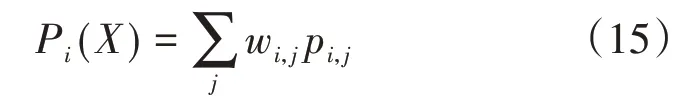
上式中的特征点对应j个参数需要被约束,其中pi,j表示第i个特征点的第j个参数的罚函数,wi,j表示第j个参数的罚函数对应的权重。
除了状态约束之外,为了减小飞控系统操纵的剧烈程度即增加轨迹的跟踪特性,还需要对相邻轨迹片段控制量变化率的差异进行约束。式(14)中的Fj表示第j个轨迹片段与第j+ 1个轨迹片段的控制量变化率之差所表征的罚函数:

此外,为了防止之前的状态约束过于严苛,从而导致无解的情况发生,还应该约束各个状态不能超过临界值。在式(14)中共有l个状态需要被约束,K为一个较大的正值,gk表示第k个参数对应的罚函数,其表达式如下形式:

上式中x表示状态,xmin,xmax表示x的临界最小值和最大值。
3 最优“S”形战术机动控制模型
本文选取“S”形战术机动进行建模与分析。“S”形战术机动一般用在超视距空战阶段,可用于摆脱目标机机载雷达稳定跟踪,从而隐蔽接敌;也可用于在被动态势下,破坏目标机导弹发射条件,从而寻找机会进行反击。对“S”形战术机动分析可知:“S”形战术机动的形成原因主要是UCAV 进行有规律的滚转和偏航,如图2所示。
在“S”形战术机动轨迹上设置5 个特征点,相邻两个特征点之间的轨迹分为6 个片段,总共划分成24 个轨迹片段。在AB 段,UCAV 滚转角从0∘开始不断减小,在B 点减至最小,偏航角也从0∘开始不断减小;在BC 段,UCAV 滚转角开始增加,在C点增加至0∘,而偏航角由于滚转角为负而继续减小,在C 点减至最小;在CD 段,UCAV 滚转角从0∘开始增加,在D 点增至最大,偏航角开始增加;在DE 段,UCAV 滚转角开始减小,在E 点减小至0∘,而偏航角由于滚转角为正而继续增加,在E 点增至0∘附近。为了表征5 个特征点,现列出特征点的位置,如表1 所示。

表1 “S”形战术机动特征点Table1 Feature points in the S-shape maneuver
下面针对特征点处的约束进行具体分析,由于“S”形战术机动具有对称性,因此可选取点A,B,C 进行分析,三个特征点处的状态罚函数如表2所示。
通过以上特征点状态罚函数的约束,可以表征“S”形战术机动的轨迹特性。除此之外,对于“S”形战术机动,还存在状态临界值约束,共有3 组,其表达式如下:

表2 “S”形战术机动特征点标准状态及其罚函数Table2 Standard states and penalty functions of feature points in the S-shape maneuver

4 SPEA2算法
4.1 Pareto最优解理论
对于多目标优化问题来说,多个优化的目标之间往往是冲突的,因此不存在某一个解能够同时使得多个目标达到最优,只能确定一组折中解,一般称为Pareto 最优解集,人们只能依据具体的需求从Pareto最优解集中选取满足自己要求的解。从广义上理解的话,在搜索空间里没有比Pareto 最优解集更好的解了。
Pareto最优解定义如下:假设求解最小值问题,F(x) =[f1(x),…,fm(x)]为目标向量,X为问题的决策空间。若不存在任何x∈X,使得fi(x) ≤fi(x∗),∀i∈{1,2,…,m},并 且 不 存 在 任 何x∈X,使 得fj(x) <fj(x∗),∃j∈{1,2,…,m},则称x∗是多目标优化问题的一个Pareto最优解[12]。
Pareto 支配关系定义如下:对于m个目标分量的最小化多目标向量F(x) =[f1(x),…,fm(x)],对于 任 意 两 个 决 策 变 量x1,x2∈X,当且仅当i∈{1,…,m}时,有fi(x1)<fi(x2),则称x1支配x2,记作x1>x2。在整个解空间S中都不被其他解支配的所有解的集合P称为Pareto最优解集。
Pareto前沿定义如下:由Pareto最优解集P中所有Pareto最优解所对应的目标函数向量组成的曲面称为Pareto前沿Pf。
4.2 SPEA2算法
SPEA2 算法是Zitzler 等在强度Pareto 进化算法(Strengthen Pareto Evolutionary Algorithm,SPEA)的基础上提出的一种改进型算法[13]。算法主要步骤如下:
Step1:初始化进化种群Pt,设置外部种群P∗t,将初始化为空集;
Step2:计算Pt和P∗t中的个体的适应度值;
Step3:环境选择:将Pt和P∗t中所有的非支配个体存入外部种群P∗t+1,如果P∗t+1中的个体数量大于外部种群容量,则对这些非支配个体进行删减;如果P∗t+1中的个体数量小于外部种群容量,则需要从进化种群选择其他支配个体存入P∗t+1;
Step4:判断是否达到种群进化条件,如果达到则将P∗t+1作为结果输出,算法结束;否则,进入下一步;
Step5:采用锦标赛选择方法从外部种群P∗t+1中选择个体作为父代种群进入交配池;
Step6:对父代种群进行交叉、变异操作,产生新一代进化种群Pt+1,令t=t+ 1,转入Step2。
SPEA2算法流程如图3所示。
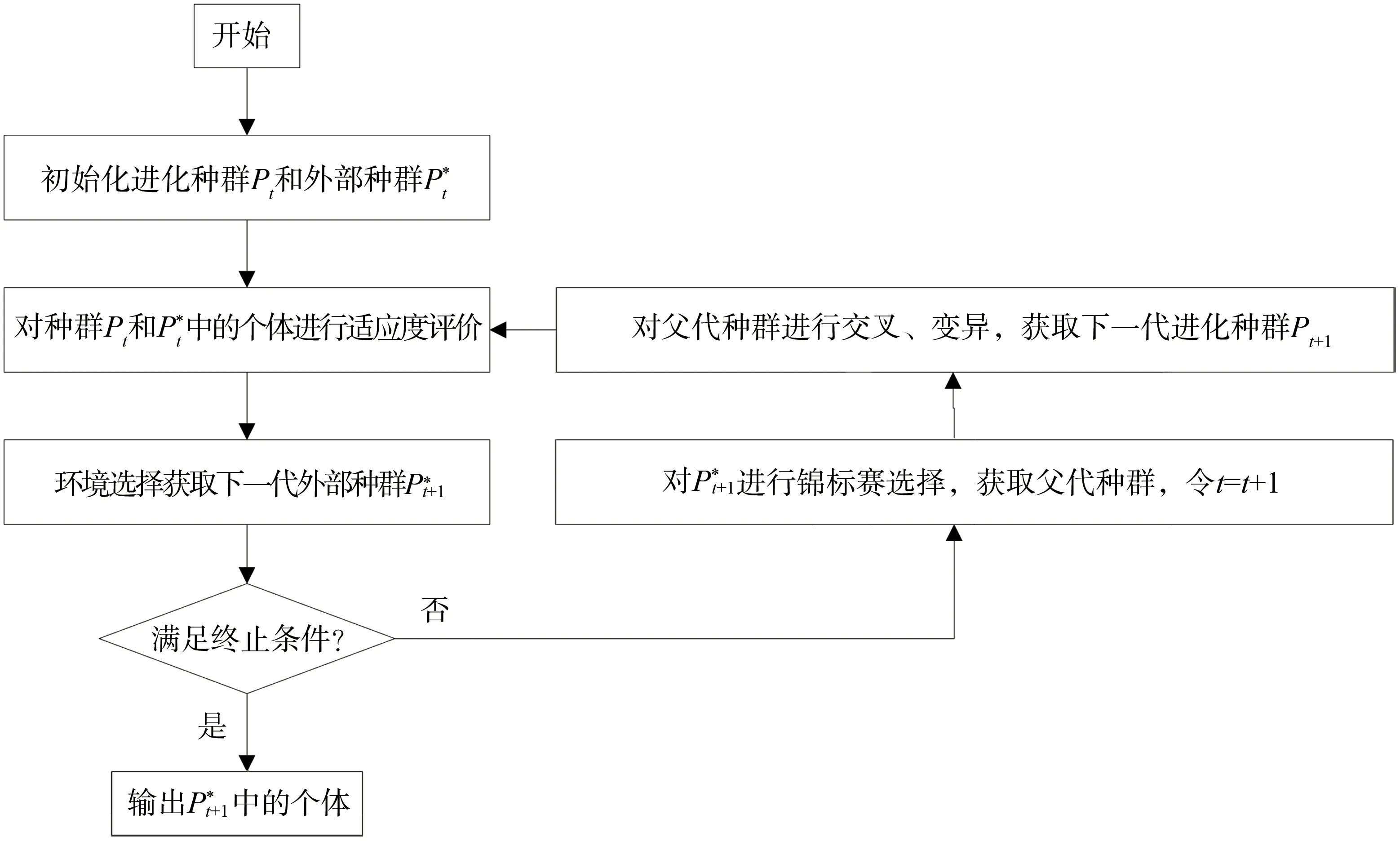
图3 SPEA2算法流程图Fig.3 Flow diagram of SPEA2 algorithm
相比于SPEA 算法,SPEA2 算法在种群个体评价机制和环境选择机制上做出了改进。为了避免出现被相同的外部种群个体支配的进化种群个体具有相同的适应度值,SPEA2 算法在计算个体适应度值时,同时考虑了该个体的支配信息和被支配信息[14]。适应度函数定义如下:
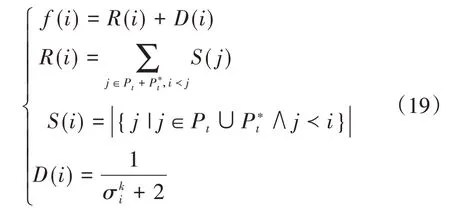
上式中S(i)表示个体i所支配的个体数量。R(i)表示所有支配i的个体j在进化种群Pt和外部种群P∗t中支配其他个体的数量和。通过R(i)对支配个体进行排序,而对于非支配个体,无法通过R(i)对其进行排序,因此,在SPEA2 中增加了个体的密度信息D(i),从而对非支配个体进行排序。式中表示个体i到第k个个体的欧式距离,其中N为进化种群的容量,M为外部种群的容量。通过上式对适应度函数的定义,不仅能得到个体的支配信息与非支配信息,还能了解个体在种群中的分布情况。
除此之外,在环境选择机制上,SPEA2 算法设置的外部种群的容量是不变的,当选出的非支配个体超过外部种群的容量时,需要对其进行删减,SPEA2 算法采用基于密度的删减策略,其基本原理就是位于密集区域的非支配个体比位于稀疏区域的非支配个体会有更大的概率被删减[15]。通过这种删减策略,相比于SPEA算法,SPEA2算法能够获得分布较好的外部种群。
5 仿真结果
仿真验证以UCAV 超视距隐蔽接敌为背景,选取迎角和滚转角作为机动轨迹规划模型的控制量,由于本次机动轨迹规划将“S”形战术机动划分成24条轨迹片段,因此最终求解的结果为一组迎角和滚转角变化率。针对“S”形战术机动设置的前三个特征点的标准状态约束,设置如下:
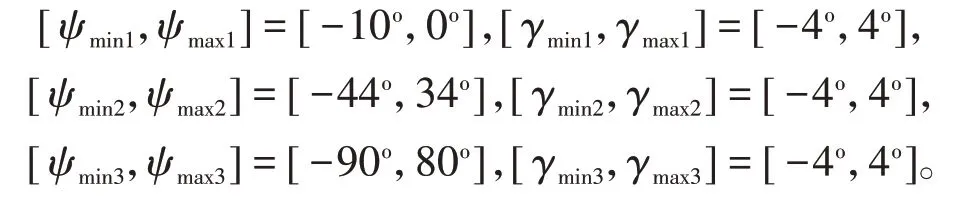
针对“S”形战术机动设置的状态临界值约束如下:[αmin,αmax]=[-5∘,20∘],[φmin,φmax]=[-65∘,65∘],[ψmin,ψmax]=[-90∘,0∘]。针对SPEA2 算法,设定进化种群容量和外部种群容量为500,染色体长度为48,交叉概率为0.95,变异概率为0.02。经过SPEA2算法求解出的Pareto前沿Pf如图4所示。

图4 Pareto前沿面Fig.4 Pareto optimal front
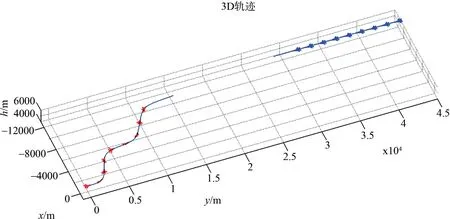
图5 UCAV超视距隐蔽接敌Fig.5 Stealthy approach to the enemy for UCAV beyond visual range
由图4可以看出,若需要J1达到最小,即轨迹的跟踪特性最好,则目标机对于UCAV 累积的威胁J2则最大;而当J1达到最大时,目标机对于UCAV累积的威胁J2最小,即UCAV 当前态势最好。现从Pareto 最优解集中选取一点(2.125,0.6765),对其进行分析,其对应的轨迹及相关状态变量曲线如图5所示。
图5 为UCAV 执行“S”形战术机动以便摆脱目标机机载雷达的稳定跟踪,从而实现隐蔽接敌的轨迹示意图。期间UCAV 的三个角度变化曲线如图6所示。

图6 UCAV航迹倾角、滚转角及偏航角曲线Fig.6 Curves of flight path angle,roll angle and yaw angle of UCAV
UCAV迎角变化曲线如图7所示。
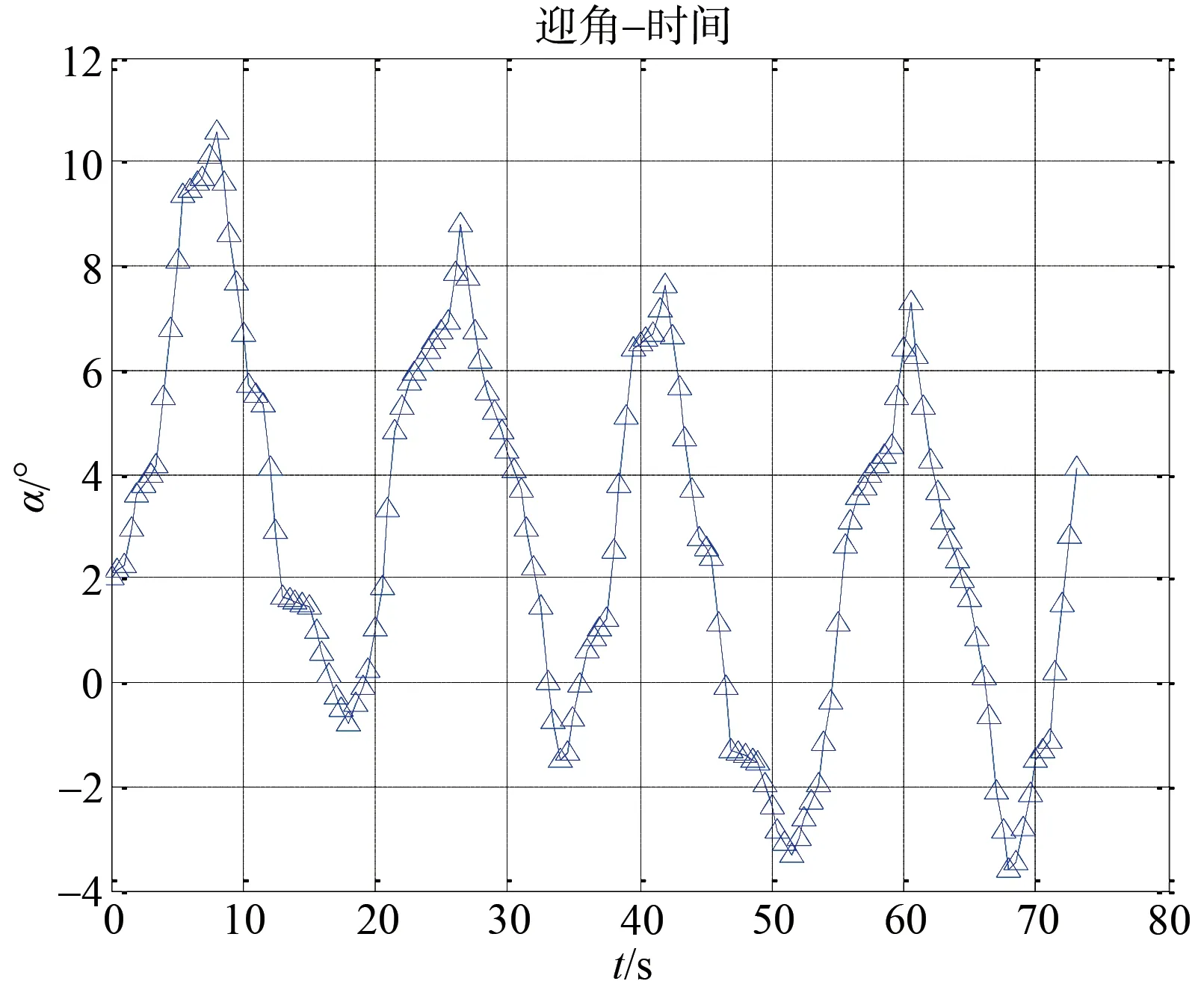
图7 UCAV迎角曲线Fig.7 Curve of angle of attack of UCAV
UCAV速度变化曲线如图8所示,UCAV所受升力、阻力及推力变化曲线如图9所示。
UCAV法向过载变化曲线如图10所示:UCAV机动轨迹规划的输入量:迎角变化率曲线如图11所示。
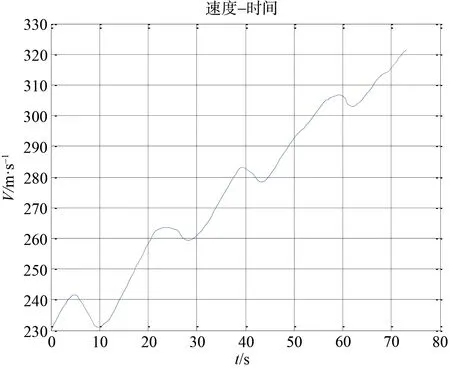
图8 UCAV速度曲线Fig.8 Curve of velocity of UCAV
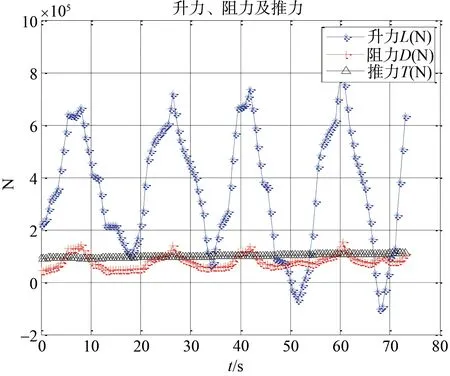
图9 UCAV所受升力、阻力及推力曲线Fig.9 Curves of lift force,air drag and thrust of UCAV

图10 UCAV法向过载曲线Fig.10 Curve of normal overload of UCAV
滚转角变化率曲线如图12所示。
UCAV与目标机机载空空导弹攻击区变化曲线如图13所示。

图11 UCAV迎角变化率曲线Fig.11 Curve of rate of angle of attack of UCAV
空战态势因子变化曲线如图14所示。
图14中红色曲线表示UCAV的空战态势因子,蓝色曲线表示目标机的空战态势因子。空战累积态势变化情况如图15所示。
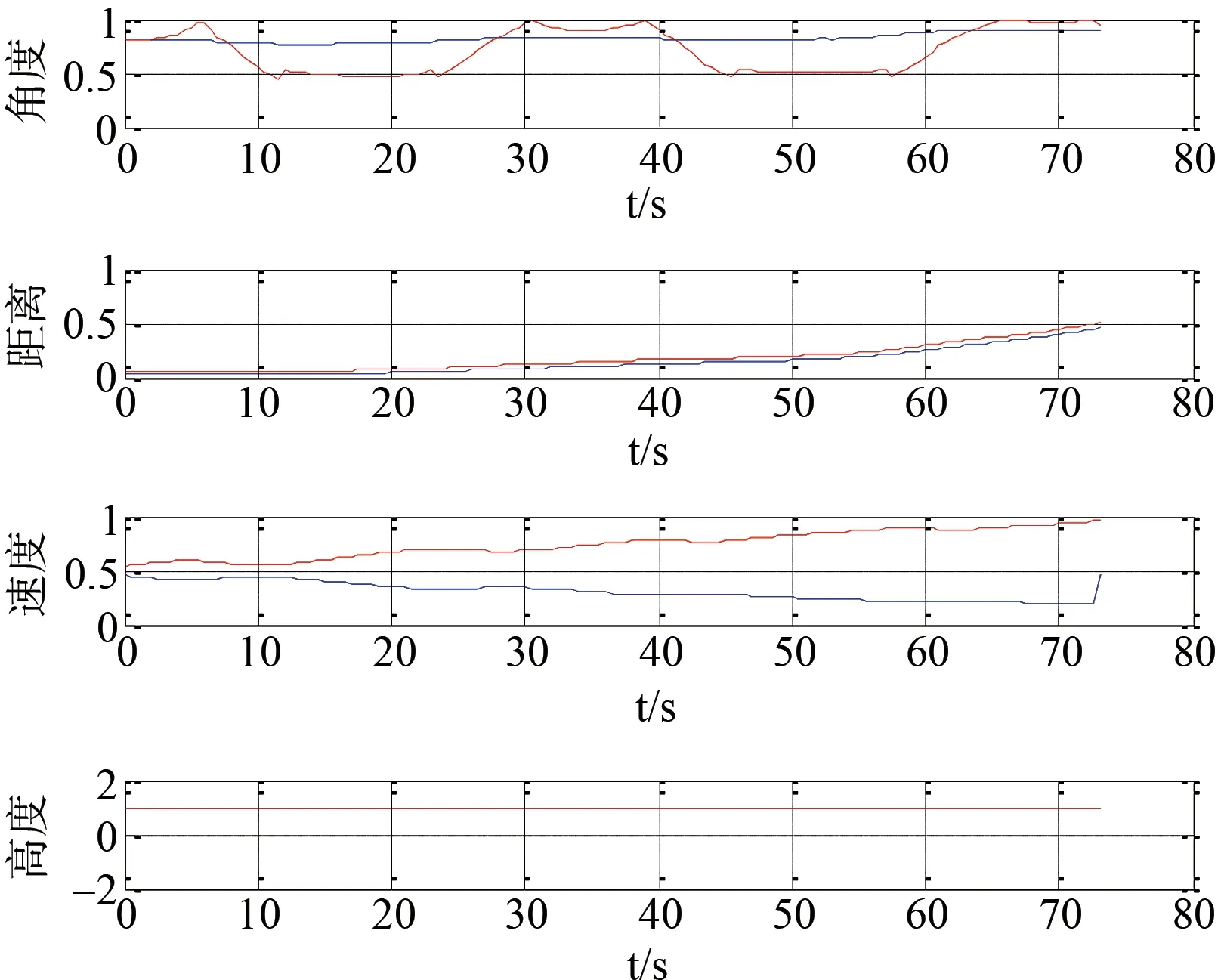
图14 空战态势因子变化曲线Fig.14 Curve of situational factors of aerial warfare
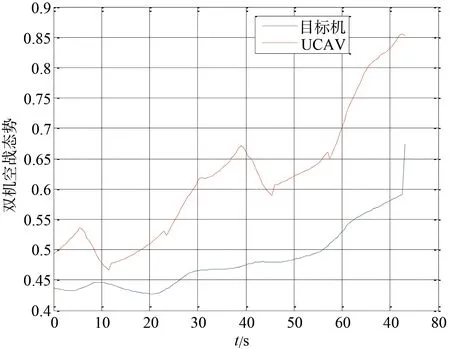
图15 空战态势变化曲线Fig.15 Curve of situation of aerial warfare
通过图15可知UCAV通过“S”形战术机动摆脱目标机机载雷达的稳定跟踪,从而实现隐蔽接敌,使得UCAV 的空战态势不断提升,最终抢先达到导弹发射条件。
6 结 论
本文在传统轨迹规划问题上,综合考虑了规划轨迹的跟踪特性与态势最优,将问题转化为多目标优化问题,利用SPEA2 算法求解出问题的Pareto 最优解集。在无法兼顾规划轨迹的跟踪特性与空战态势均为最优的情况下,求解出的Pareto 最优解集包含了优化目标不同权重时的所有最优轨迹,可根据实际需要的不同进行选择。

