一种欠驱动无人船避障及目标跟踪鲁棒控制方法
张亚博,姜 明,肖 强,王 军,陈 霖,张海燕
(1. 北京航天发射技术研究所,北京100076;2. 北京中星时代科技有限公司,北京100070)
1 引 言
无人船是一种能够在海洋环境中自主航行,并且能够完成各种海上任务的运载平台。无人船因其加工成本低、制造周期短、环境适应能力强等特点,可以用于各种海上任务。这也为进一步开发海洋资源提供了一种更为安全的方式。因此,无人船的研究已成为船舶行业的热点问题[1-2]。
为使无人船在复杂的海洋环境中具有自主航行的能力,首先需要解决其对目标的跟踪控制问题。罗伟林等[3]针对船舶航向非线性系统,提出了一种基于神经网络方法的鲁棒跟踪控制器。夏云鹏等[4]针对无人船航迹控制问题,提出了基于模拟退火优化NMPC 算法的非线性模型预测控制算法,设计了直接型无人船航迹控制器,该算法能够提高航迹控制的准确性和实时性。Breivik等[5]采用一种新的导航方法,实现了对任意路径的跟踪控制。Miao J 等[6]基于时滞控制方法和降阶线性扩展状态观测器(LESOS)技术,提出了一种改进的复合视距制导律,其能估计未知的侧滑角,并能补偿时变海流的影响。廖煜雷等[7]考虑了外界干扰以及船舶模型参数不确定的问题,采用滑模变结构控制方法,设计了轨迹跟踪控制器,通过仿真,验证了该控制器的有效性。
其次,在无人船航行的过程中,其周围的环境可能会出现紧急情况,比如航路上出现障碍物。这就需要无人船有碰撞规避的能力。对此问题刘琨等[8]提出了一种改进的人工势场法,设计了无人船碰撞规避控制算法。陈文玉[9]对无人船的避碰算法问题,基于改进的人工势场法进行了规则约束下具体避碰算法的设计与实现。
本文针对欠驱动无人船的碰撞规避和目标跟踪问题,提出了一种基于滑模变结构控制和改进人工势函数理论的控制方法。首先建立了考虑不确定干扰和参数摄动的无人船水平面二阶非线性动力学模型,通过引入滑模控制方法为其设计了目标跟踪鲁棒控制器。同时基于改进人工势函数设计了无人船碰撞规避控制算法。最后对设计的控制算法进行了稳定性证明和数值仿真。仿真结果表明,提出的控制方法在无人船做平面运动时可以有效进行目标跟踪和碰撞规避。
2 无人船动力学模型
为描述无人船的运动,首先引入两个参考坐标系,即地面坐标系Se和船体坐标系Sb,如图1 所示。地面坐标系用来描述船在惯性系下的位置和姿态,选取地球表面任意位置为其原点,X轴指向正北方向,Y轴指向正东方向,Z指向地心方向,Y轴与X轴、Z轴构成右手坐标系。船体坐标系用来描述船舶的受力和速度,其固连于船体,坐标原点位于船体质心,x轴沿径向指向船头,y轴指向右舷,z轴垂直于xy平面并指向船底方向。z轴与x轴、y轴构成右手坐标系。

图1 无人船水面运动模型Fig.1 Motion model of unmanned ship
考虑到实际情况,在研究无人船运动控制过程中,一般忽略船舶垂荡、横摇和纵摇运动,只讨论无人船在水平面的纵荡、横荡和艏摇运动。同时,考虑无人船在运动过程中受到的风、浪等环境引起的扰动未知但有界,则无人船的运动模型可以由式(1)、(2)描述。
η̇=J(η)v(1)Μv̇+C(v)v+D(v)v=τT+τE(2)其中η=(x y ψ)T为无人船的位置状态,x、y分别表示无人船在地面坐标系中的位置,ψ表示无人船的艏向角。v=(u υ r)T表示无人船的速度状态,各分量分别表示在船体坐标系中的纵向速度、横向速度和偏航角速度。τT=(Fu0Nr)T表示无人船的控制,其中Fu表示无人船受到的纵向推力,Nr表示无人船受到的偏航力矩。τE=(τuE τυE τrE)表示无人船受到的环境干扰以及动力学方程中的参数摄动。J(η)为地面坐标系到船体坐标系的转换矩阵,Μ是船舶的惯量矩阵,一般无人船是左右对称前后不对称的,但通常来说m23=m32≈0,因此为简单分析,本文假定Μ是一个对角正定矩阵,C(v)表示科里奥利/向心力矩阵,D(v)是阻尼矩阵,此处将阻尼中的非线性部分考虑在了系统的扰动参数中,因此此处只考虑线性阻尼。各矩阵具体的值为:
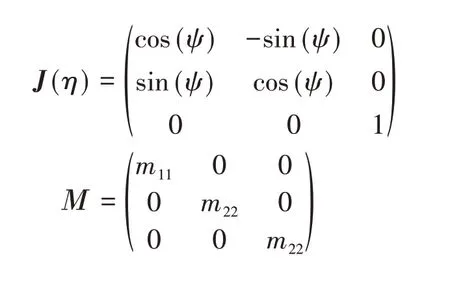
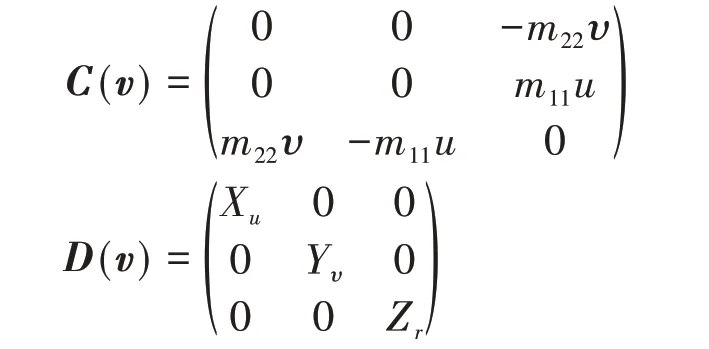
其中不确定项τE可以由式(3)描述

无人船数学模型中的惯性矩阵、阻尼矩阵等都是与无人船本身属性有关的常量,一般称之为模型参数,在对算法做仿真验证时,必须利用这些参数构建数学模型。对于一艘特定的无人船,这些参数的值是确定的。然而,这些参数的获取是比较困难的,需要通过大量的航行实验数据,使用参数辨识理论获得。本文采用最小二乘算法对研究无人船运动控制问题需要的参数进行了辨识。在系统辨识前,首先对无人船动力学方程进行了小角度线化,然后对线性化之后的动力学方程采用最小二乘算法进行参数辨识。表1给出最终的辨识结果。

表1 无人船模型参数辨识结果Table1 Parameter identification results of unmanned ship model
其中m11、m22表示无人船的广义质量,m33表示无人船广义转动惯量。Xu、Yv、Zr分别表示无人船沿本地坐标系三轴的阻尼。
3 无人船目标跟踪及碰撞规避鲁棒控制方法
3.1 控制方法设计
滑模控制能够有效克服系统的不确定性,对干扰和未建模动态具有很强的鲁棒性,且具有响应迅速、物理实现简单等优点。本文将以滑模控制方法为基础实现无人船的控制。
首先对无人船的动力学模型进行变换,为对各个状态进行统一的分析,将式(1)(2)合并为一个二阶方程。对式(1)求导得到式(4):

令
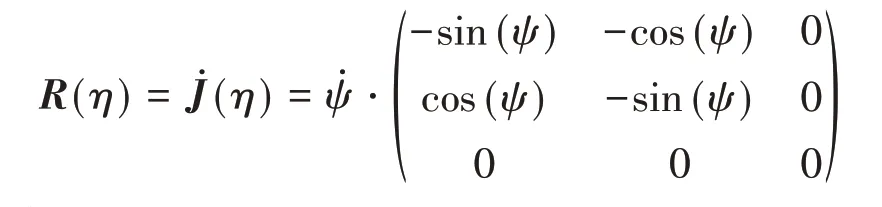
得到
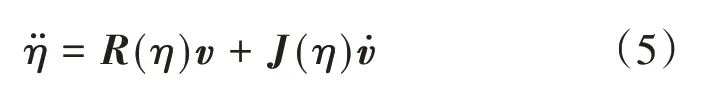
又

将式(6)、(7)代入式(5)可以得到

进一步可以写为

设
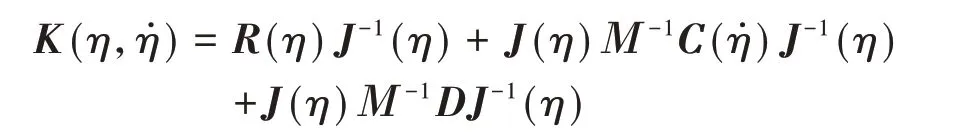
上式可以改写为

令无人船的目标状态为,可以求得当前状态和目标状态的偏差为
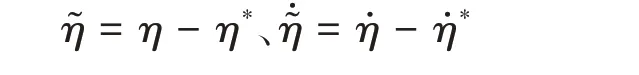
选取滑动面为

其中Λ=diag{λr},λr>0,r=1,2,3,显然滑动面上的状态运动是稳定的。接下来设计到达运动,对式(11)的滑动面函数求导。本文研究无人船对点目标的目标跟踪问题,因此有= 0= 0。可以对滑动面求导公式做进一步化简:

选择到达控制律为:

式中H,ε∈R3×3。为了消除滑动运动在滑模面上的抖颤,在此处选择饱和函数sat(x)代替符号函数。

其中φ为饱和函数边界层厚度。对比式(12)、(13)可以得到等效控制为:
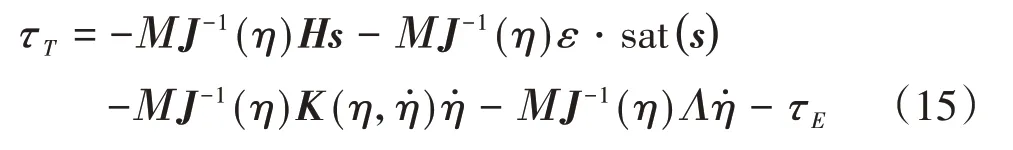
式(15)控制中存在不确定参数,无法直接使用,为消去不确定参数,首先采用式(16)控制进行替换:
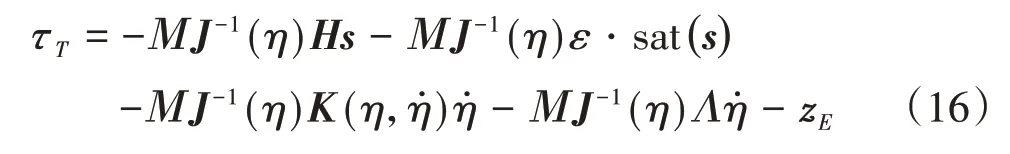
为确定zE,将式(16)代入式(12)中得到式(17):
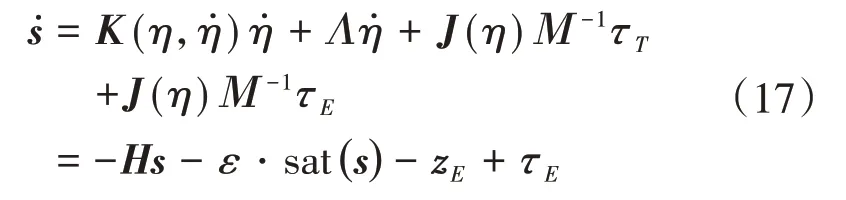
又滑模控制到达条件为:
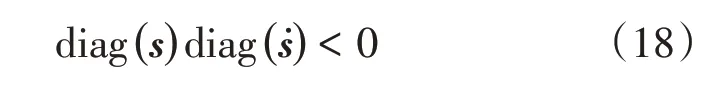
将式(17)带入式(18)之后写成分量形式得到式(19):

因此为使得滑模控制到达条件满足,比较式(19)各项大小可以得到:
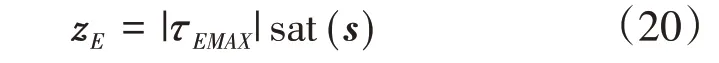
式(16)、(20)构成了无人船鲁棒控制律,该控制率能够实现无人船对点目标的跟踪,并且对干扰具有较强的鲁棒性。但是在无人船实际航行的过程中,很有可能在规划的运动路径上发现障碍物,因此无人船设计碰撞规避的控制是很有必要的,本文接下来的部分将详细叙述关于无人船碰撞规避的控制。
3.2 无人船碰撞规避控制设计
为提高无人船在真实环境中的自主运行能力,且使得无人船在运行过程中受到各种不确定干扰的情况下仍然能够顺利完成任务,在无人船进行了目标跟踪的前提下,需要进行碰撞规避的设计。本小节将利用人工势场函数理论为无人船设计碰撞规避控制。
人工势场法是通过构建虚拟的势能场,使无人船沿着势能场的趋势进行运动,最终到达目的地的一种方法。这是一种非最优的机动策略,但相对于其他算法具有反应快速、计算简单以及实时性强等优点,对算法加以改进能在无人船路径规划任务中得到很好的应用。
本文前面部分已经完成了无人船从起始点到目的地的控制设计问题,因此本文的对障碍物的碰撞规避问题只需要考虑障碍物和无人船之间的斥力。这能够避开同时存在引力和斥力时进入局部极小值的问题。
大多数人工势场的斥力势场函数都是以无人船与障碍物的相对位置的倒数为自变量的二次函数,无人船小幅度地移动就能引起势场强度大幅度的变化,即斥力场强度变化较快。而在实际应用中,斥力场强度的数值变化过快会影响对运动路径的判断,对斥力常量的选择要求较为苛刻,指数型势函数能够有效避免此问题,因此本文构建式(21)所示的指数型势函数:

式(21)对η求导得到:
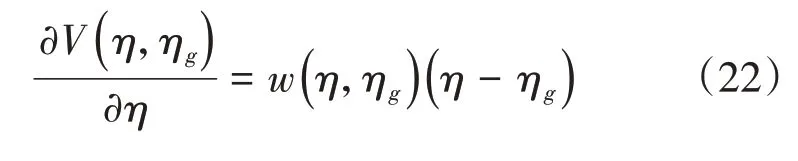
其中

式(21)中,V(η,ηg)表示势函数,ηg表示障碍物的位置,Q为正定对称阵,λ1、λ2为相对近距离限制参数,通过调整Q、λ1、λ2可以实现无人船和障碍物的距离大于设计的最小距离,从而防止碰撞的发生。下面将对上述势函数进行仿真,直观地观察其变化规律。
从图2 可以看出,随着无人船和障碍物的距离减小,人工势函数将增大,无人船受到的斥力也会增加,该斥力能够控制无人船远离障碍物,从而实现碰撞规避。
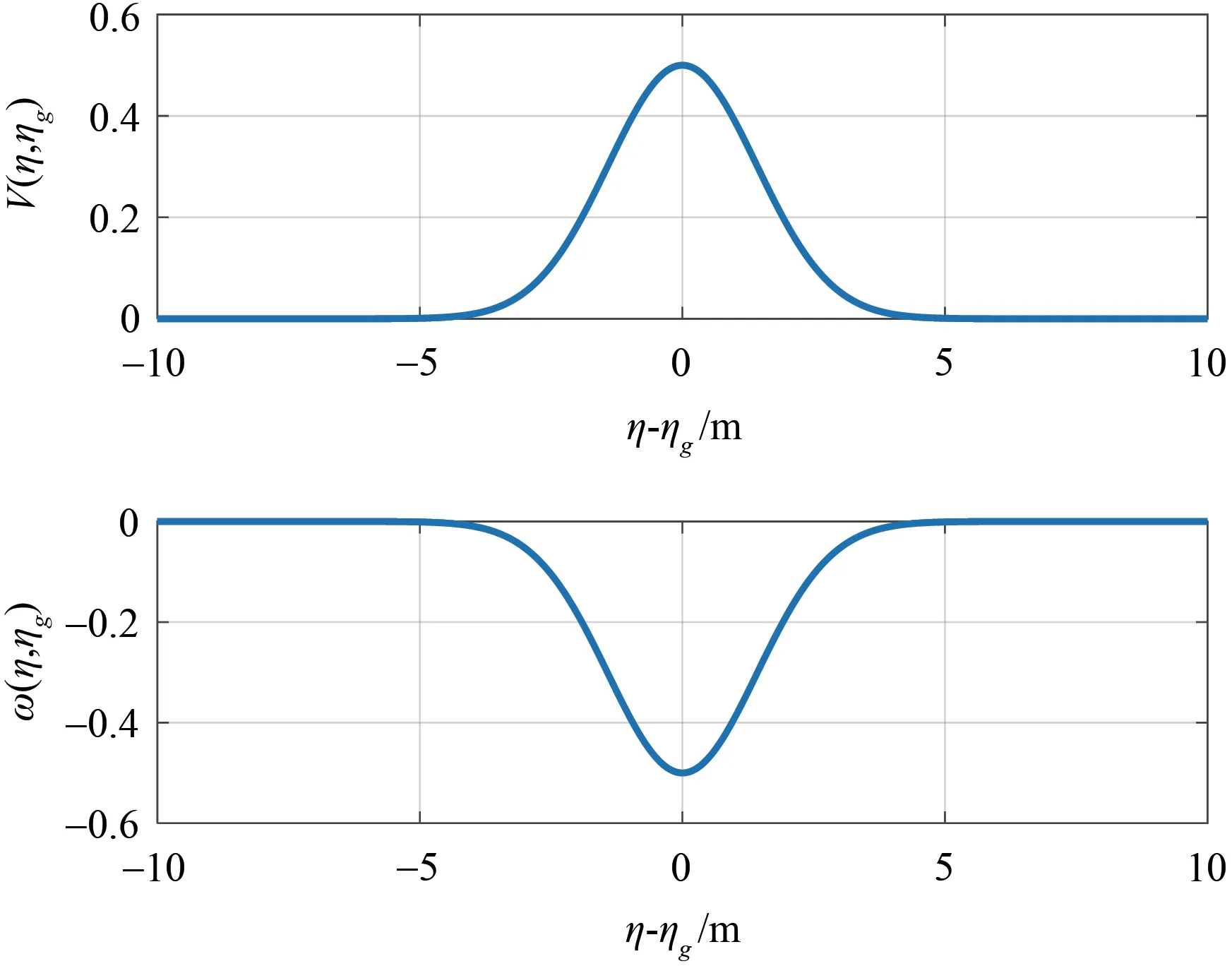
图2 势函数模型仿真Fig.2 Potential function model simulation
4 控制器的稳定性证明
前两节设计了无人船目标跟踪和碰撞规避算法,本小节将证明上面设计的算法的稳定性。首先选择李雅普诺夫函数为:
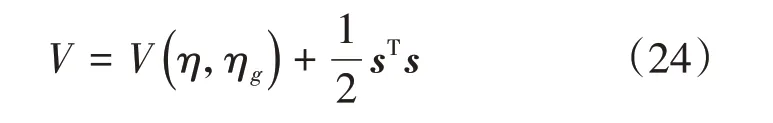
对上面函数求导得到:

根据zE的求解过程可以看出,式(25)中后三项的和是小于0 的。对于第一项,显然当无人船在障碍物附近运动时,η̇Tw(η,ηg)(η-ηg)<0,进一步可以得到上面定义的李雅普诺夫函数对时间的导数小于0,因此设计的控制能够使得该系统稳定。
5 数值仿真
为验证设计的目标跟踪和碰撞规避控制器的性能,本文对此控制器进行数值仿真。仿真中假设无人船和目标距离1000m 以内时,文中设计的碰撞规避算法开始运行。仿真用到的具体的参数设置如下。控制器的参数选择为H=10-2×I3×3、ε=10-7×I3×3、Λ=10-2×I3×3。

表2 无人船状态信息Table2 State of unmanned ship
从图3、4可以看出,随着时间的推移,无人船的各个状态均达到了其期望值,由此可以证明本文设计的目标跟踪控制的有效性。在大概600s左右,无人船在障碍物附近重新调整了路线,绕开了障碍物。
从图5 可以明显看出,当无人船在运动过程中遇到障碍物时,能够及时调整自己的位置,最终避开障碍物且到达期望的位置,这也说明本文设计的碰撞规避算法能够实现无人船的避障。
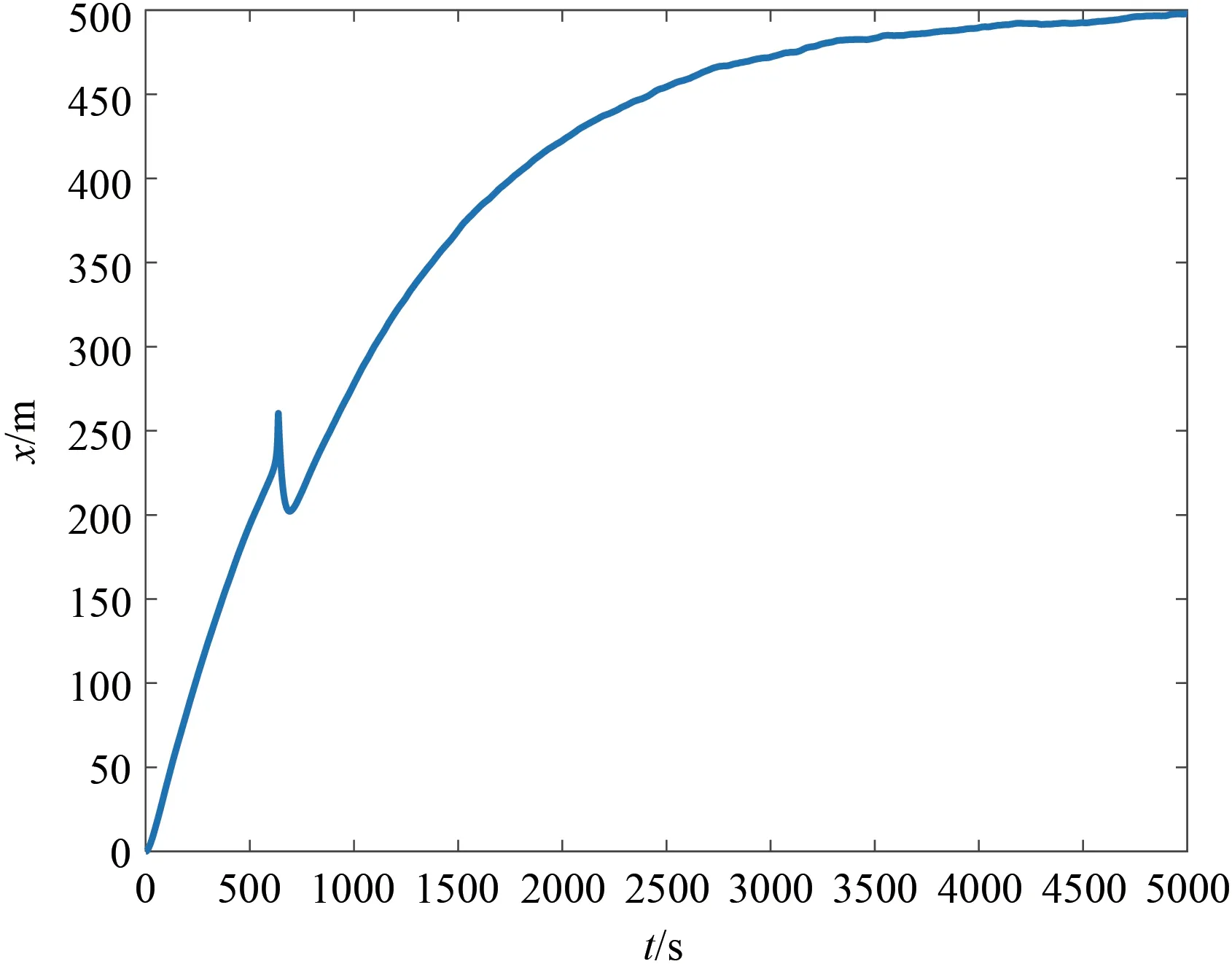
图3 无人船x坐标Fig.3 X coordinate of unmanned ship

图4 无人船y坐标Fig.4 Y coordinate of unmanned ship

图5 无人船运动轨迹Fig.5 Trajectory of unmanned ship
6 结 论
本文针对欠驱动无人船的碰撞规避和目标跟踪问题,提出了一种基于滑模变结构控制和改进人工势函数理论的控制方法。建立了考虑不确定干扰和参数摄动的无人船水平面二阶非线性动力学模型,并为其设计了基于滑模控制的目标跟踪鲁棒控制器,同时基于改进人工势函数设计了无人船碰撞规避控制算法。最后对设计的控制算法进行了稳定性证明和数值仿真。仿真结果表明,提出的控制方法在无人船做平面运动时可以有效进行目标跟踪和碰撞规避。

