基于单值中智集的火电机组主蒸汽温度控制系统多属性性能评价

郑渭建，蒋雄杰，刘 霜，王印松，李牡丹，李士哲



基于单值中智集的火电机组主蒸汽温度控制系统多属性性能评价

郑渭建1，蒋雄杰2，刘 霜3，王印松3，李牡丹3，李士哲3

（1.浙江浙能技术研究院有限公司，浙江 杭州 310000； 2.浙江浙能嘉华发电有限公司，浙江 嘉兴 314000； 3.华北电力大学控制与计算机工程学院，河北 保定 071000）

工业控制系统中采用单一运行数据对其进行性能评价的研究较多，采用多属性性能评价的研究较少。本文针对火电厂生产过程对主蒸汽温度控制系统控制品质的要求，提出一种基于单值中智集的火电机组主蒸汽温度控制系统多属性性能评价方法。首先，根据火电机组主蒸汽温度控制系统运行数据的多个属性值建立中智集决策矩阵；然后，基于每个属性提供的信息确定反映决策者意见的单值中智集决策矩阵，并通过加权平均算子将所有个体决策矩阵聚合为共同决策矩阵；最后，根据计算出的待评价控制方案与中智集正负理想解之间的欧式距离建立的相对贴近度函数的大小来评价各控制方案，并确定最优控制方案。仿真结果表明该评价方法有效合理且计算简单。

单值中智集；主蒸汽温度系统；多属性性能评价；欧式距离；相对贴近度函数；安全运行

复杂工业过程一般包含诸多控制回路，随着时间推移，常出现被控对象特性发生变化或执行机构老化等现象，造成控制器性能下降，影响经济效益甚至带来安全隐患。目前，工业控制系统大多通过人工分析系统运行数据进行系统评价，这与当前控制系统自动化水平不相适应；且分析人员知识结构不同，不同分析人员对控制系统的性能评价结果也不相同，控制系统性能评价的准确性有待检验。因此，研究控制系统性能评价方法，对实际控制系统进行监视和评价，协助操作人员分析系统运行情况，从而减轻工作人员的工作量，同时保证系统工作在良好运行状态，具有重要意义[1]。

控制系统性能大致分为随机性性能、确定性性能和鲁棒性性能。其中，对控制系统鲁棒性性能的评价方法研究较少，对其他两种性能的评价方法研究较多。文献[2]提出针对单回路控制系统的最小方差指标性能评价方法，采用自相关函数诊断闭环控制系统性能。文献[3-4]对反馈控制系统、前馈-反馈复合控制系统及串级控制系统的性能进行研究，进一步拓展了文献[2]中方法的应用范围。文献[5]根据反馈不变项理论，从方差的意义上对串级系统的控制性能进行评价，所提出的方法计算简单且可靠性高。文献[6]对同步发电机励磁系统设计最小方差控制器,并将其作为系统控制性能上限，与系统实际性能进行比较得到性能指标。仿真结果表明该方法能够准确地评估同步发电机励磁控制系统的性能。文献[7-8]采用数据的协方差指标对多变量控制系统进行性能评价，验证了协方差指标在多变量控制系统性能评价方面的有效性。文献[9]提出基于实时协方差指标的预测模型，以预测残差对模型预测控制器进行性能评价。文献[10]通过比较基准数据与监测数据的评价指标（IAE）对有积分过程的控制回路进行评价，并给出PID控制参数的重新整定方法。文献[11]在级联控制系统存在非高斯干扰情况下，基于信息理论和最小熵标准给出控制性能评价指标。文献[12]根据控制系统时域性能指标，提出一种针对负荷控制系统性能的评价方法。文献[13]基于积分平方误差（ISE）和总误差平方变化（TSV）指标，将其下限作为性能评价基准，比较在线ISE和TSV值与评价基准值制定性能评价指标，并应用于带前馈的单变量控制系统的性能评价。综上可见，目前大多控制器性能评价方法只考虑了控制系统单一方面的性能，很少同时研究控制系统的随机性性能和确定性性能。

近年来，综合考虑多种性能评价的多属性决策理论发展迅速。多属性决策模型可以描述为以属性权重归一化后的量化属性评价值为基础，通过决策方案效用函数集成综合评价指标，最后决策待评价方案的优劣。文献[14]通过多属性决策方法改进案例检索策略，并运用多目标评价准则对参数整定后的PID控制效果进行评价。文献[15]首先通过历史数据建立系统评价的基准，然后应用多属性决策方法得到其综合属性评价值，并通过TE过程证明了该方法的有效性，但文中未给出该方法中属性权重的确定方法。文献[16]提出了基于信息熵的多属性性能评估模型，实现炉焦加热燃烧过程优化控制系统的在线性能评估，并针对控制系统性能评估不合格的情况，在线调节控制器参数。总之，基于多属性决策理论的性能评估方法效果良好，但在过程控制领域中的应用仍较少。

主蒸汽温度是评价火电机组运行安全性的重要参数之一，具有大惯性、大迟延及非线性等特点，其过髙或过低及大幅波动都将严重影响锅炉和汽轮机的安全经济运行[17-18]。当负荷、燃料量、主蒸汽压力、磨煤机的切换、减温水流量及给水温度等发生变化时，主蒸汽温度均会产生不同程度的波动。因此，对主蒸汽温度控制系统进行性能评价尤为重要。

本文基于多属性决策理论，综合考虑控制器的随机性性能与确定性性能，针对火电机组主蒸汽温度控制系统提出了一种基于单值中智集的多属性性能评价方法。通过控制系统运行数据的多个属性值建立中智集决策矩阵，并基于决策者重要程度和属性重要程度确定权重，通过加权平均算子将所有反映个体的决策矩阵聚集为共同决策矩阵；最后构建相对贴近度函数，并根据相对贴近度函数值对各控制方案进行排序，从而确定最优控制方案。

1 过热蒸汽温度控制系统特性

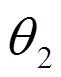
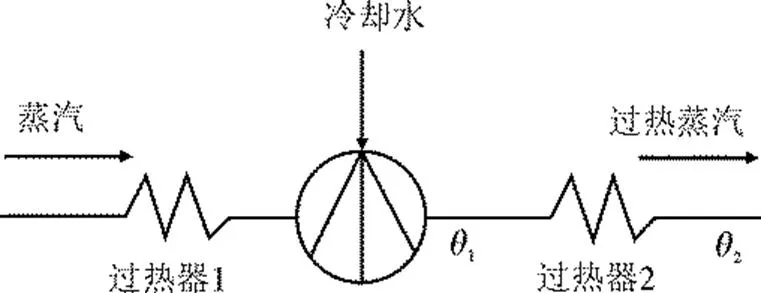
图1 过热蒸汽温度控制过程

目前，绝大多数电厂采用图2所示的串级PID控制策略对过热蒸汽温度进行控制。图2中：1()和2()分别为被控对象导前区和惰性区传递函数，c1()和c2()分别为主、副回路PID控制器，()为给定值，()为控制器输出，1为经喷淋水冷却后测量的蒸汽温度，2为输出测量值。串级PID控制有利于快速消除内回路扰动，但主调节器的控制性能对对象模型参数时变的鲁棒性和适应性的影响至关重要。

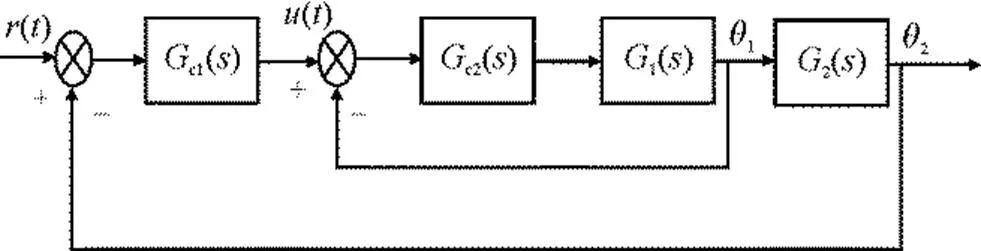
图2 过热蒸汽温度串联PID控制策略

一般来说，串级PID控制系统的内回路比较容易整定，外回路的整定较难达到最佳效果[19-20]。现场整定一般将经验整定法和试凑法相结合。主蒸汽温度这类非线性时变的复杂对象，控制系统性能的优劣受负荷、燃料量、主蒸汽压力、给水流量等扰动影响较大。

2 控制性能多属性决策

2.1 控制性能的多属性评价指标

多属性决策的主要目标是确定待评价方案的优劣。方案的本质特征通过多个属性体现。该方案中的某个属性是对其某方面特征的描述，这种描述既可以是定性的，如好、中、差等语言变量，也可以是定量的，如属性的具体值。

多属性决策问题数学表述为：令={1,2,…,x}为属性集合，f()为属性值，其中(=1,2,…,)，()=[1(),2(),…, f()]，多属性决策的目的是达到最理想的值。

控制系统性能评价的目的主要是评价控制器的性能优劣。综合考虑控制器的随机性与确定性性能指标，选取了控制系统的峰值时间1、最大动态偏差2、调节时间3、误差绝对值积分指标(IAE)4、穿越次数5这5个时域性能指标。当选取的性能指标值均最小时，控制性能最好。然而，由于PID控制器某些性能相互冲突，在实际中不可能同时获得最佳值，因此需要确定各指标在系统性能评价时的权重。多属性决策方法综合考虑了控制系统的确定性和随机性，特别是在各属性重视程度不同的情况下，避免了单一属性评价的片面性。

2.2 基于单值中智集的多属性决策方法

2.2.1 中智集及其相关定义

中智集起源于中性哲学，反映原点自然和中立的范围及其交互及不同观念的范围[21]。

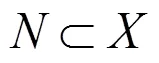
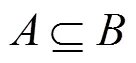
2.2.2单值中智集

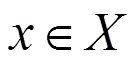
2.2.3 基于单值中智集的多属性决策

考虑多属性决策问题有个离散的供选择的方案集={1,2, …,A}和个属性集={1,2, …,C}。假设由决策者为各属性提供的权重向量是={1,2,…,}，该权重向量与最初建立的决策矩阵无关。根据需要决策问题的描述，建立决策矩阵。初始决策矩阵为

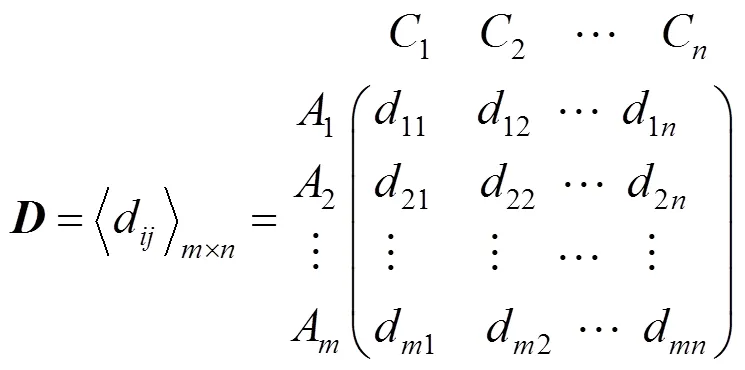
每个方案的每个属性都用单值中智集表达，则决策矩阵变为

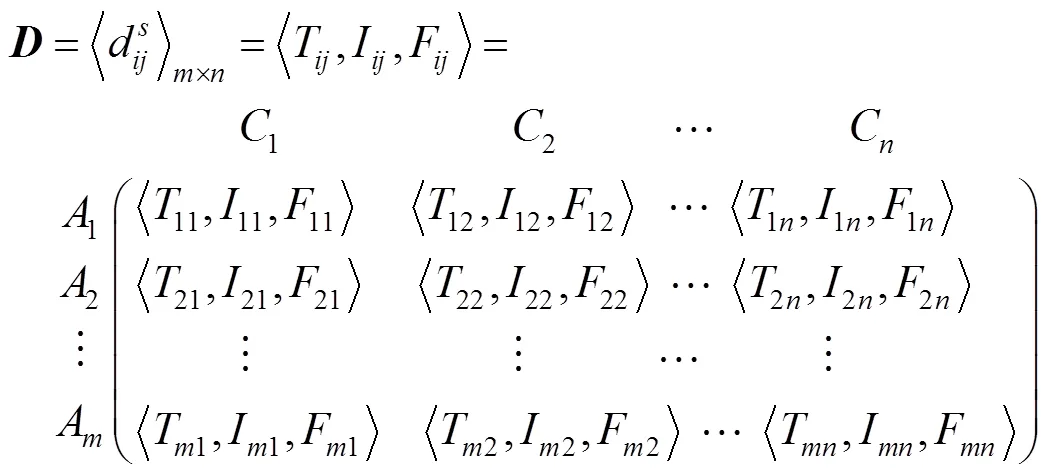
将单值中智集的区域按等级划分为3类[26]： 1）可接受的中智集等级；2）不确定的中智集等级；3）不可接受的中智集等级。

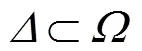
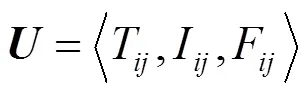
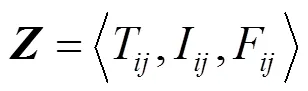
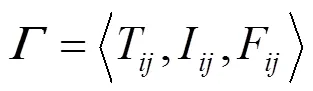
定义7 将单值中智集

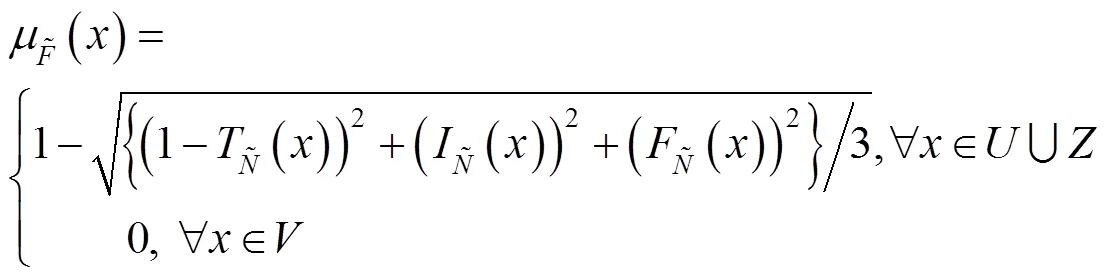
2.2.4 考虑决策者权值的多属性决策矩阵

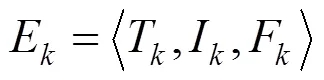
由式(1)可得第个决策者的权值表达为

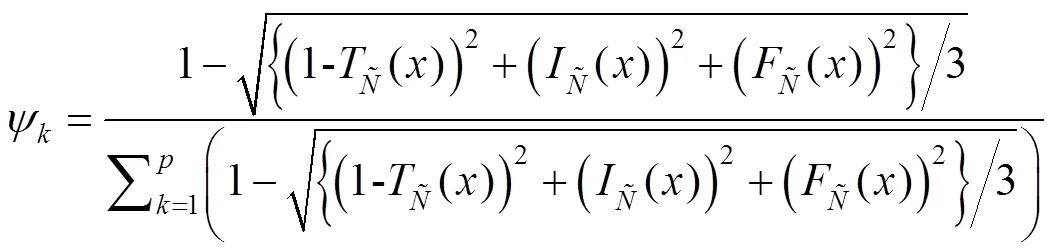
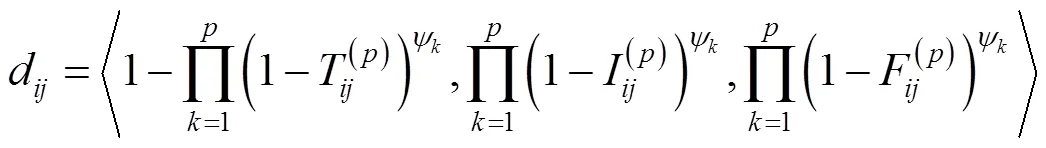
其中，=1,2,…,，=1,2,…,。

2.2.5 考虑属性权值的多属性决策矩阵

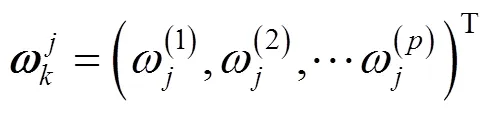
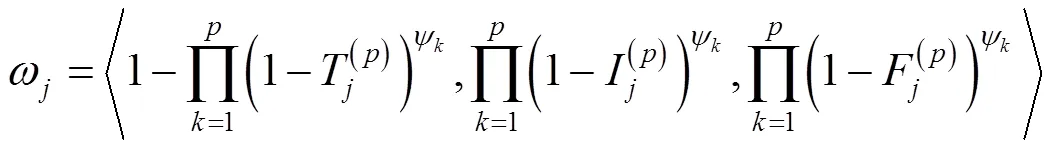
式中=1,2,…,。

将所得到的属性权值和考虑决策者权重的中智集决策矩阵进一步聚合。由定义5可得

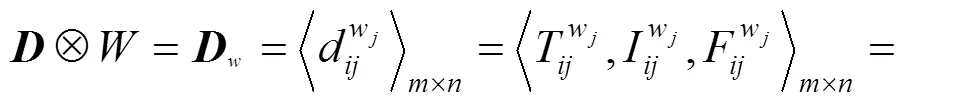
2.2.6 中智集相对正理想解和相对负理想解

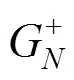
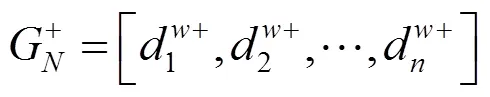
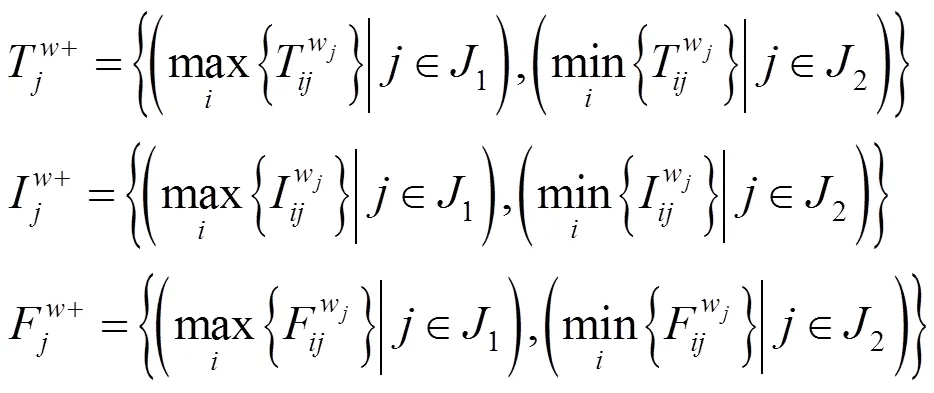
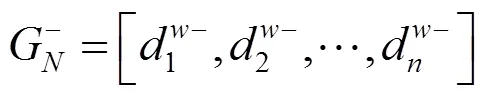
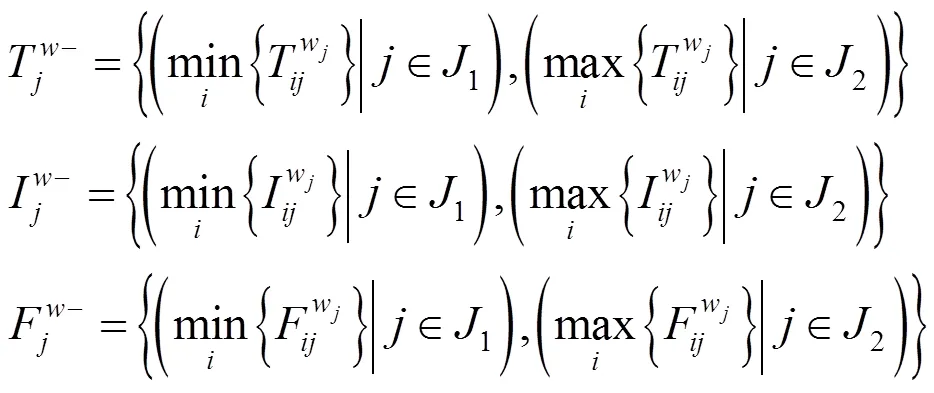
2.2.7 中智集正理想解的相对贴近度

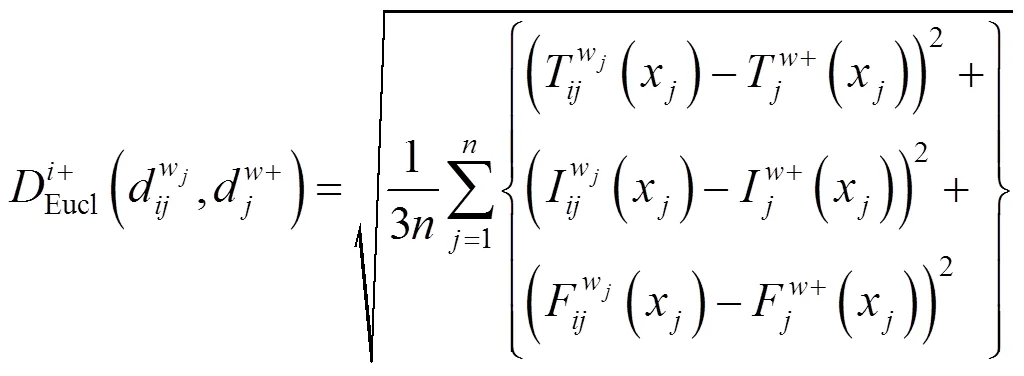
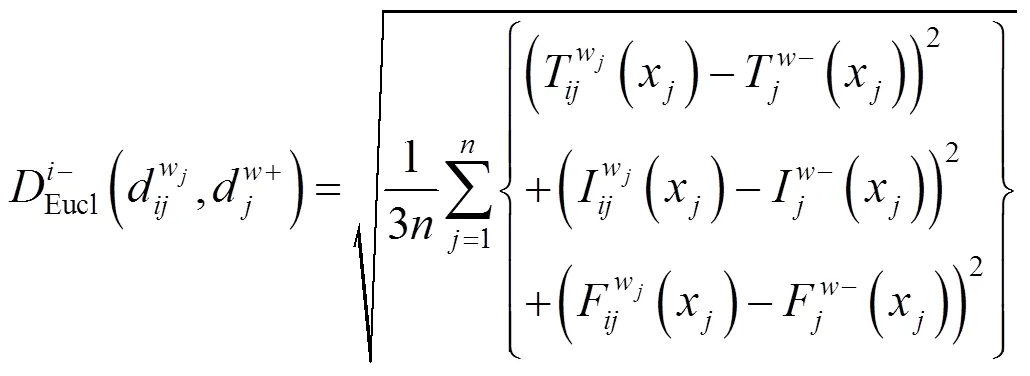
每个方案关于中智集正理想解的相对贴近 度为

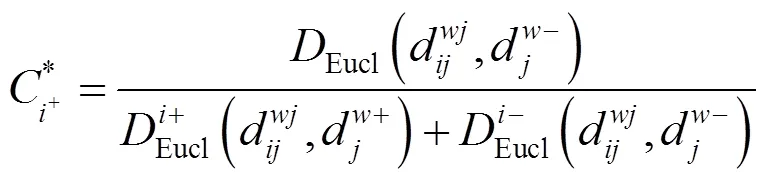
3 系统仿真

主蒸汽温度串级PID控制系统主要有100%、75%、50%和37%共4种典型工况，负荷几乎不会降至37%以下运行。但在37%工况时，PID的控制效果会相对差一些，本文以评价多种PID控制方案的效果好坏为目的，故选用容量为600 MW机组的超临界锅炉37%工况进行性能评价。亦可选用其他工况的控制系统进行性能评价。主蒸汽温度串级PID控制系统[28]控制结构如图2所示，导前区和惰性区传递函数为

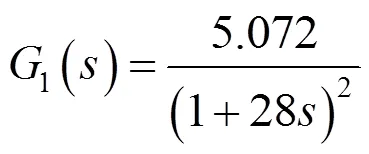
在位于主回路的过热蒸汽温度控制对象中，存在更多的复杂性和非线性，使其难以有效控制。相比之下，副回路控制对象相对简单，并且可以在很大程度上视为线性，故其副回路控制器选择比例控制器，其中p2=0.3。主回路采用的控制器结构为PID()=P+I/+D。

为验证本文提出的基于单值中智集的多属性性能评价方法的有效性，考虑4个决策制定者DM1 （专家）、DM2（学生）、DM3（操作者）、DM4（工程师），计划从4组不同的主回路控制器参数备选方案（PID1、PID2、PID3、PID4）中选择最合适的控制方案，其中每个方案考虑5个属性。分别为峰值时间1、最大动态偏差2、调节时间3、误差绝对值积分指标4、穿越次数5，控制器参数及输出属性值见表1。机组主蒸汽温度动态响应曲线如图3所示。具体的评价实施步骤分为以下4个步骤。

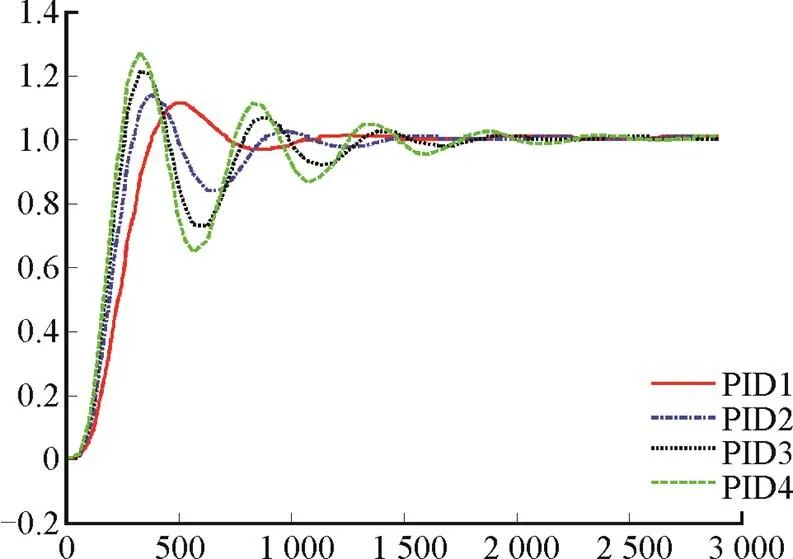
图3 机组主蒸汽温度控制系统动态响应曲线

表1 控制器参数及输出属性值

Tab.1 The controller parameters and output attribute values

1）计算决策者权值

由于每个决策者的经验地位有差异，很难用一个具体数表示决策者意见的重要程度，往往采用“很好”、“很强”、“很弱”等概念来表述，利用单值中智数表示的决策者等级语言变量（表2）将决策者的意见转化为中智数，本例中4个决策者的重要程度的单值中智集语言关系见表3。

表2 单值中智数表示的决策者等级语言变量

Tab.2 A decision maker’s rank linguistic variable expressed by a single valued middle intelligence number

表3 决策者重要程度的单值中智集语言关系

Tab.3 The single valued Chi sets language relations of decision maker importance

2）基于决策者评价构建聚合决策者权值的中智集决策矩阵

基于单值中智集的属性语言关系见表4。由4个决策者提供的每个方案的相关属性评价值见表5。

表4 基于单值中智集的属性语言关系

Tab.4 The attribute language relations based on single valued Chi sets

表5 4个决策者关于每个方案的属性评价

Tab.5 The attribute evaluation of each decision by four decision makers

由式(4)和式(5)可得11=1–(1–0.5)0.284 5×(1–0.8)0.173 3×(1–0.65)0.255 7×(1–0.65)0.284 5=0.648 4

11=(0.5)0.284 5×(0.2)0.173 3×(0.35)0.257 7×(0.35)0.284 5=0.351 6

11=(0.45)0.284 5×(0.15)0.173 3×(0.3)0.257 7×(0.3)0.284 5=0.298 6

同理可得聚合决策者评价的中智集决策矩阵（表6）。

表6 聚合决策者评价的中智集决策矩阵

Tab.6 The decision matrices of Chi sets evaluated by aggregate decision makers

3）构建聚合属性权值的中智集决策矩阵

考虑每个决策者认为方案中的属性重要程度不同，给出属性权重评价见表7。

表7 决策者给出的属性权重评价

Tab.7 The attribute weight evaluation given by decision maker

由式(6)可得每个属性的聚合权重向量（表8）。由式(7)并结合表6和表8，计算可得聚合加权的中智集决策矩阵（表9）。例如：

表8 聚合属性权重向量

Tab.8 The weight vectors of aggregated attributes

表9 聚合加权中智集决策矩阵

Tab.9 The decision matrix of Chi sets in aggregate weighting

4）计算相对贴近度

首先，确定中智集决策矩阵正负理想解，所采用的5个评价属性均为成本型属性，评价实际数据时，同一属性越小的数据评价等级越高，故由式(9)、式(10)可得

标准的欧式距离由式(10)、式(11)确定，每个方案关于中智集正理想解的相对贴近度由式(12)确定。各个方案与理想解的标准欧式距离及相对贴近度见表10。

表10 各方案与理想解的标准欧式距离及相对贴近度

Tab.10 The standard Euclidean distance and relative closeness of the schemes and the ideal solutions

文献[19]的相似贴近度值对PID1和PID2的控制性能区分较小，本文方法较好地区分了两者的差异，可以确定PID1的控制性能好。当采用PID3和PID4控制时，系统的动态响应曲线波动较大，控制系统性能较差，通过表10和图4也可看出其相对贴近度较小。分析可见：PID1控制性能最好，PID4控制性能最差。这与图3反映的各方案控制效果一致，验证了本文提出方法与实际情况相符合。

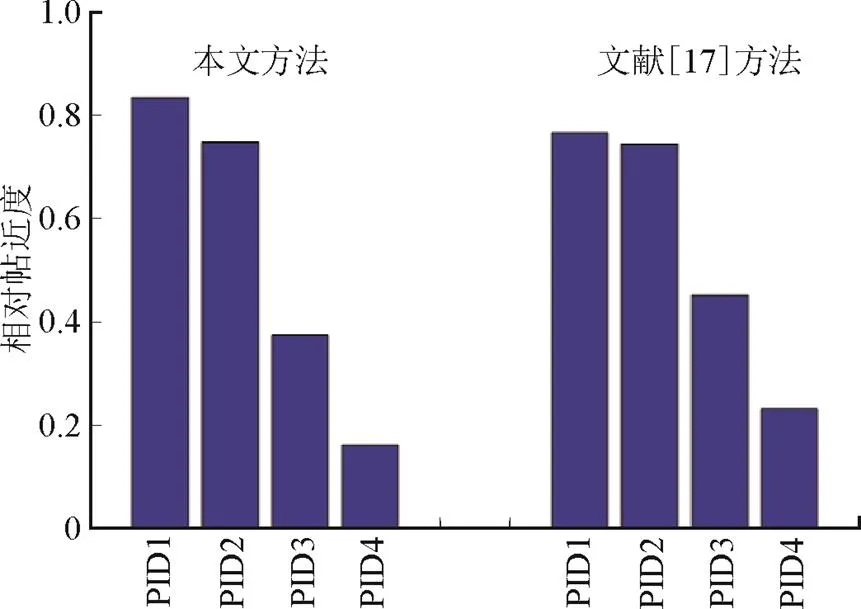
图4 相对贴近度对比

4 结 语

本文针对火电机组主蒸汽温度串级PID控制，介绍了一种基于单值中智集的多属性决策控制系统性能评价方法。通过考虑不同的决策者评价意见来分配决策者权重及属性权值，并将权重分配进行单值中智集聚合，综合考虑控制器随机性与确定性性能，得到较全面的评价结果。

由于该方法通过控制系统实际输出数据来计算评价基准，因此评价结果更接近实际情况。限于篇幅，本文仅针对4个PID控制方案进行对比评价。该方法也可用于设定值改变、不同扰动及不同控制策略等情况下的控制系统性能评价。由于该方法不需要建立控制系统的精确数学模型，只需对控制系统的输出数据进行分析处理，算法简单，解决了控制器性能的综合评价问题，对电厂自动化水平的进一步提高有重要的意义。

［1］ 王茂海, 赵玉江, 齐霞, 等. 电网实际运行环境中相量测量装置性能在线评价方法[J]. 电力系统保护与控制, 2015, 43(6): 86-92. WANG Maohai, ZHAO Yujiang, QI Xia, et al. Proposal of index for PMU field performance evaluation in actual operating environment[J]. Power System Protection and Control, 2015, 43(6): 86-92.

［2］ HARRIS T. Assessment of closed loop performance[J]. Canadian Journal of Chemical Engineering, 1989, 67(5): 856-861.

［3］ DESBOROUGH L, HARRIS T. Performance assessment measure for univariate feedback control[J]. Canadian Journal of Chemical Engineering, 1992, 70(6): 1186-1197.

［4］ CHEN J, HUANG S C, YEA Y. Achievable performance assessment and design for Parallel cascade control systems[J]. Journal of Chemical Engineering of Japan, 2005, 38(3): 188-201.

［5］ 杨政厚, 房方, 刘吉臻. 串级控制回路的性能评价方法[J]. 动力工程, 2009, 29(5): 426-431. YANG Zhenghou, FANG Fang, LIU Jizhen. Performance assessment method for cascade control loop[J]. Chinese Journal of Power Engineering, 2009, 29(5): 426-431.

［6］ 张虹, 徐滨, 高健, 等. 基于最小方差基准的励磁系统性能评估[J]. 电力系统保护与控制, 2014, 42(8): 54-58. ZHANG Hong, XU Bin, GAO Jian, et al. Performance assessment of excitation system based on minimum variance benchmark[J]. Power System Protection and Control, 2014, 42(8): 54-58.

［7］ QIN S J, YU J. Recent developments in multivariable controller performance monitoring[J]. Journal of Process Control, 2007, 17(3): 221-227.

［8］ YU J, QIN S J. Statistical MIMO controller performance monitoring, Part II: Performance diagnosis[J]. Journal of Process Control, 2008, 18(3/4): 297-319.

［9］ 田学民, 史亚杰, 曹玉苹. 基于协方差指标预测的MPC实时性能监控[J]. 自动化学报, 2013, 39(5): 658-663. TIAN Xuemin, SHI Yajie, CAO Yuping. Real-time performance monitoring of MPC based on covariance index prediction[J]. Journal of Automation, 2013, 39(5): 658-663.

［10］ WANG Y, LI S, TIAN J, et al. Performance assessment of thermal power plant load control system based on covariance index[J]. Control Engineering Practice, 2016, 54: 58-69.

［11］ ZHANG J, ZHANG L, CHEN J, et al. Performance assessment of cascade control loops with non-Gaussian disturbances using entropy information[J]. Chemical Engineering Research & Design, 2015, 104: 68-80.

［12］ 李士哲, 王印松, 张涛, 等. 基于时域指标的负荷控制系统性能评价[J]. 控制工程, 2016, 23(6): 864-869. LI Shizhe, WANG Yinsong, ZHANG Tao, et al. Performance assessment of load control system based on time domain index[J]. Control Engineering of China, 2016, 23(6): 864-869.

［13］ TAN K K, LEE T H, JIANG X. Robust on-line relay automatic tuning of PID control systems[J]. ISA Transactions, 2000, 39(2): 219-232.

［14］ 严爱军, 于远航. 基于案例推理的PID控制器参数认知整定方法[J]. 信息与控制, 2015, 44(5): 525-530. YAN Aijun, YU Yuanhang. Cognitive tuning method based on case-based reasoning for PID controller’s parameters[J]. Information and Control, 2015, 44(5): 525-530.

［15］ 齐良才, 李宏光. 基于数据驱动的控制器性能多属性评价方法[J]. 华东理工大学学报(自然科学版), 2014, 40(2): 244-249. QI Liangcai, LI Hongguang. A multi-attribute assessment method of controller performance based on data- driven[J]. Journal of East China University of Science and Technology (Natural Science Edition), 2014, 40(2): 244-249.

［16］ 雷琪, 颜慧, 吴敏. 基于多属性性能评估的焦炉加热燃烧过程在线优化控制方法[J]. 化工学报, 2015, 66(1): 307-315. LEI Qi, YAN Hui, WU Min. An on-line optimal control method for combustion process of coke oven based on multi-attribute performance evaluation[J]. CIESC Journal, 2015, 66(1): 307-315.

［17］ YU Z, WANG J. Performance assessment of static lead-lag feedforward controllers for disturbance rejection in PID control loops[J]. ISA Transactions, 2016, 64: 67-76.

［18］ KO B S, EDGAR T F. Performance assessment of cascade control loops[J]. Aiche Journal, 2000, 46(2): 281-291.

［19］ YU J, QIN S J. Statistical MIMO controller performance monitoring, part I: data-driven covariance benchmark[J]. Journal of Process Control, 2008, 18(3/4): 277-296.

［20］ MASSIMILIANO V, ANTONIO V. Performance assessment and retuning of PID controllers for integral processes[J]. Journal of Process Control, 2010, 20: 261-269.

［21］ BISWAS P, PRAMANIK S, GIRI B C. TOPSIS method for multi-attribute group decision-making under single-valued neutrosophic environment[J]. Neural Computing and Applications, 2016, 27(3): 727-737.

［22］ WANG H, SMARANDACHE F, ZHANG Y, et al. Single valued neutrosophic sets[J]. Rev Air Force Acad, 2010, 17: 4-10.

［23］ 王坚强, 李新蛾. 基于多值中智集的TODIM方法[J]. 控制与决策, 2015, 30(6): 1139-1142. WANG Jianqiang, LI Xin’e. TODIM method based on multi valued Chi sets[J]. Control and Decision, 2015, 30(6): 1139-1142.

［24］ LIU P, WANG Y. Multiple attribute decision-making method based on single-valued neutrosophic normalized weighted Bonferroni mean[J]. Neural Computing and Applications, 2014, 25(7/8): 2001-2010.

［25］ MAJUMDAR P, SAMANTA S K. On similarity and entropy of neutrosophic sets[J]. Journal of Intelligent & Fuzzy Systems, 2014, 26(3): 1245-1252.

［26］ YE J. A multicriteria decision-making method using aggregation operators for simplified neutrosophic sets[J]. Journal of Intelligent & Fuzzy Systems, 2014, 26(5): 2459-2466.

［27］ DEZERT J. Open questions on neutrosophic inference[J]. Multiple-Valued Logic, 2002, 8(3): 439-472.

［28］ LIANG G, LI W, LI Z. Control of superheated steam temperature in large-capacity generation units based on active disturbance rejection method and distributed control system[J]. Control Engineering Practice, 2013, 21(3): 268-285.

Multi-attribute performance evaluation of main steam temperature control system based on single-valued neutrosophic sets

ZHENG Weijian1, JIANG Xiongjie2, LIU Shuang3, WANG Yinsong3, LI Mudan3, LI Shizhe3

(1. Zhejiang Energy Group Research Institute Co., Ltd., Hangzhou 310000, China; 2. Zhejiang Zheneng Jiahua Power Generation Co., Ltd., Jiaxing 314000, China; 3. School of Electrical and Electronic Engineering, North China Electric Power University, Baoding 071000, China)

In the industrial control system, there are many researches on performance evaluation with single running data, and less on multi-attribute performance evaluation. Against the requirement of main steam temperature control system in production process of thermal power plants, a multi-attribute performance evaluation method for the main steam temperature control system of thermal power units based on the single-valued neutrosophic set is proposed. Firstly, the neutrosophic set decision matrix is established based on multiple attribute values of the operating data of the main steam temperature control system of thermal power units. Then, on the basis of the information provided by each attribute, a single-valued neutrosophic set decision matrix that reflects the opinions of the decision maker is determined, and all the individual decision matrixes are aggregated into a common decision matrix by a weighted average operator. Finally, each control scheme is evaluated based on the degree of the relative closeness function which is calculated based on the Euclidean distance between the calculated control plan and the positive and negative ideal solutions of the neutrosophic set, and the optimal control plan is determined. The simulation results show that the proposed method is effective and reasonable, and the calculation is simple.

single valued neutrosophic set, main steam temperature system, multi-attribute performance evaluation, Euclidean distance, relative closeness function, safe operation

Fundamental Research Funds for the Central Universities (2017MS189, 9161715008); Hebei Higher Education Teaching Reform Project (2016GJJG318)

郑渭建(1973—)，男，高级工程师，主要研究方向为热工技术管理和自动化应用，zwj_411@126.com。

TP273

B

10.19666/j.rlfd.201806133

郑渭建, 蒋雄杰, 刘霜, 等. 基于单值中智集的火电机组主蒸汽温度控制系统多属性性能评价[J]. 热力发电, 2019, 48(4): 68-76. ZHENG Weijian, JIANG Xiongjie, LIU Shuang, et al. Multi-attribute performance evaluation of main steam temperature control system based on single-valued neutrosophic sets[J]. Thermal Power Generation, 2019, 48(4): 68-76.

2018-06-26

中央高校基本科研业务费专项资金资助(2017MS189, 9161715008)；河北省高等教育教学改革项目(2016GJJG318)

刘霜(1994—)，女，硕士研究生，主要研究方向为控制工程，284235641@qq.com。

（责任编辑 杜亚勤）