基于自适应变分模态分解的佤语孤立词 共振峰估计

杨建香,佘玉梅,傅美君,和丽华,解雪琴,潘文林

(1.云南民族大学 数学与计算机科学学院，云南 昆明 650500；2.西南交通大学 信息科学与技术学院，四川 成都 611756)

本文课题来源于教育部、国家语委2015年启动的中国语言资源保护工程(简称“语保工程”)，该工程开展多年以来，录制了大量少数民族语言和地方性方言，并人工对其进行了国际音标标注，但在抽样检查中发现标注信息并没有达到可信可用的程度.如果再次对语料库标注信息进行人工校对，需要花费大量人力物力，因此语言学家急需一个国际音标自动标注系统.而要完成该系统，首先，需识别语料，再进行语料自动标注.本文选用语料库中的佤语[1]为研究对象.

当准周期脉冲激励进入声道时会引起共振发生，从而产生一组共振频率，这样的一组共振频率称之为共振峰频率，简称共振峰[2].共振峰参数由共振峰频率和频带宽度(带宽)组成.而共振峰是区分不同元音的重要参数，正常情况下，一个元音会产生3～5个共振峰，依次记为F1，F2，F3，F4，F5，一般F1，F2，F3，足以描述元音的声学特性.共振峰信息包含在语音信号的频谱包络中，谱包络中的极大值对应的频率值就认为是共振峰频率.

目前，国内外对共振峰的研究主要基于语音信号的2种模型：语音信号的线性模型[3-4]和语音信号的非线性模型[5-7].线性模型主要的研究方法有：倒谱法[8-9]、 线性预测编码(linear predictive coding,LPC)[3-10]等.杨鸿武[8]等提出一种利用加权Mel倒谱(weighted mel-cepstrum,WMCEP)提取语音信号共振峰的算法，该方法比倒谱法提取的共振峰误差更小，在噪声环境下具有较好的鲁棒性.赵毅[9]等提出一种基于倒谱变换的共振峰频率检测算法，删除伪峰值和甄别合并共振峰，克服倒谱方法用于共振峰频率检测的固有缺陷.BS Atal[3]等提出一种分析提取共振峰的方法.郁伯康[10]等提出采用相频特性与对数幅频特性提取语音信号共振峰，更有效地解决共振峰合并问题，提取到更精确的语音信号共振峰参数.非线性模型主要的研究方法有：经验模态分解(empirical mode decomposition,)[11]、集合经验模态分解(ensemble empirical mode decomposition,)[12]、局部均值分解(local mean decomposition,)[13]、变分模态分解(variational mode decomposition,)[14]等.Huang[15]等提出一种基于希尔伯特-黄变换(Hilbert-Huang transform,)的语音共振峰频率估计方法，研究结果表明，基于的语音共振峰估计方法不仅能更清晰地描述语音信号的非线性和非平稳性，且能较好的描述语音信号的共振峰频率.Zhao[16]等提出一种结合和的语音信号共振峰提取算法，该算法的误差优于加权倒谱法，当信噪比很小时，仍能准确提取共振峰.但其他的非线性方法，用在共振峰提取领域还处于空白状态.针对少数民族语音识别方向所存问题，前期已获得部分相关研究成果，陈绍雄等[17]实现了基于HTK的佤语孤立词识别；杨花等[18]通过语谱图特征，运用支持向量机实现普米语语谱图识别；郭琳等[19]研发了一种人机交互语音切分系统，完成大规模的语音语料切分工作。

1 变分模态分解法

1.1 变分模态分解法基本原理

本征模态函数(intrinsic mode function,IMF)是一个窄带调频—调幅信号，其基本形式为：

uk(t)=Ak(t)cos(φk(t)).

(1)

式中，Ak(t)为uk(t)的瞬时振幅.ωk(t)为uk(t)的瞬时频率，如下所示.

(2)

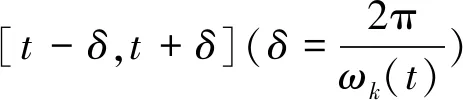
1)变分问题的构造

在确保各IMF之和等于输入信号x(t)的条件下，构造K个IMF分量uk(t)，使每个IMF的估计带宽之和最小.

① 将信号通过希尔伯特变换，得到每个IMF的解析信号和单边频谱.

(3)

式中，δ(t)为脉冲函数，H(uk(t))为希尔伯特变换作用于信号uk(t)的结果，“*”表示卷积运算.

② 加入指数项调整每个IMF的中心频率，将每个IMF的频率调制到相应基频带上.

(4)

③ 求解解调信号的梯度，并计算梯度的L2-范数，估计各IMF的带宽，假定信号x(t)被分解出K个IMF分量，则对应的约束变分模型如(式5).

(5)

式中，{uk}={u1,…,uK}代表原始信号x(t)经过分解后得到的K个IMF分量，{ωk}={ω1,…,ωK}表示相应的IMF分量的中心频率.

2)变分问题的求解

① 引入二次惩罚因子α和Lagrange算子λ(t)，将条件约束变分问题转换为无条件约束变分问题，其中α可保证信号x(t)的重构精度，Lagrange算子λ(t)可加强约束，则拓展的Lagrange如(6)所示.

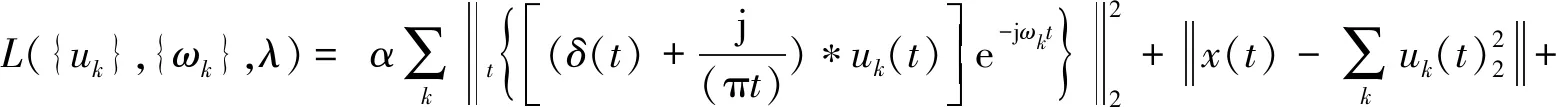
(6)

(7)

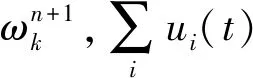
(8)

用ω-ωk代替第一项的变量ω，有：

(9)

将(9)转换为非负频率区间的积分形式，如(10)所示.

(10)

于是待求解的二次优化问题解如(11)所示.

(11)

根据同样的过程，把中心频率的取值问题也转换到频域上，得(12).

(12)

(13)

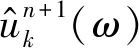
根据上述分析，求解流程如下.

Step 2n=n+1，执行整个外循环；

Step 3 根据(12)和(13)更新uk与ωk；

Step 4k=k+1，重复Step 3执行内循环，直至k=K；

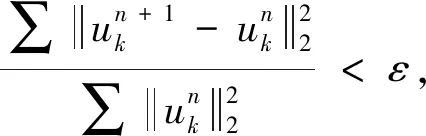
1.2 变分模态分解法仿真实例

已知周期信号x(t)，如(14).

x(t)=x1(t)+x2(t)+x3(t).

(14)

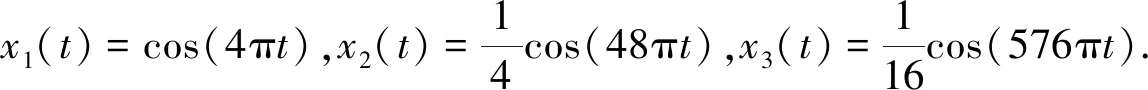
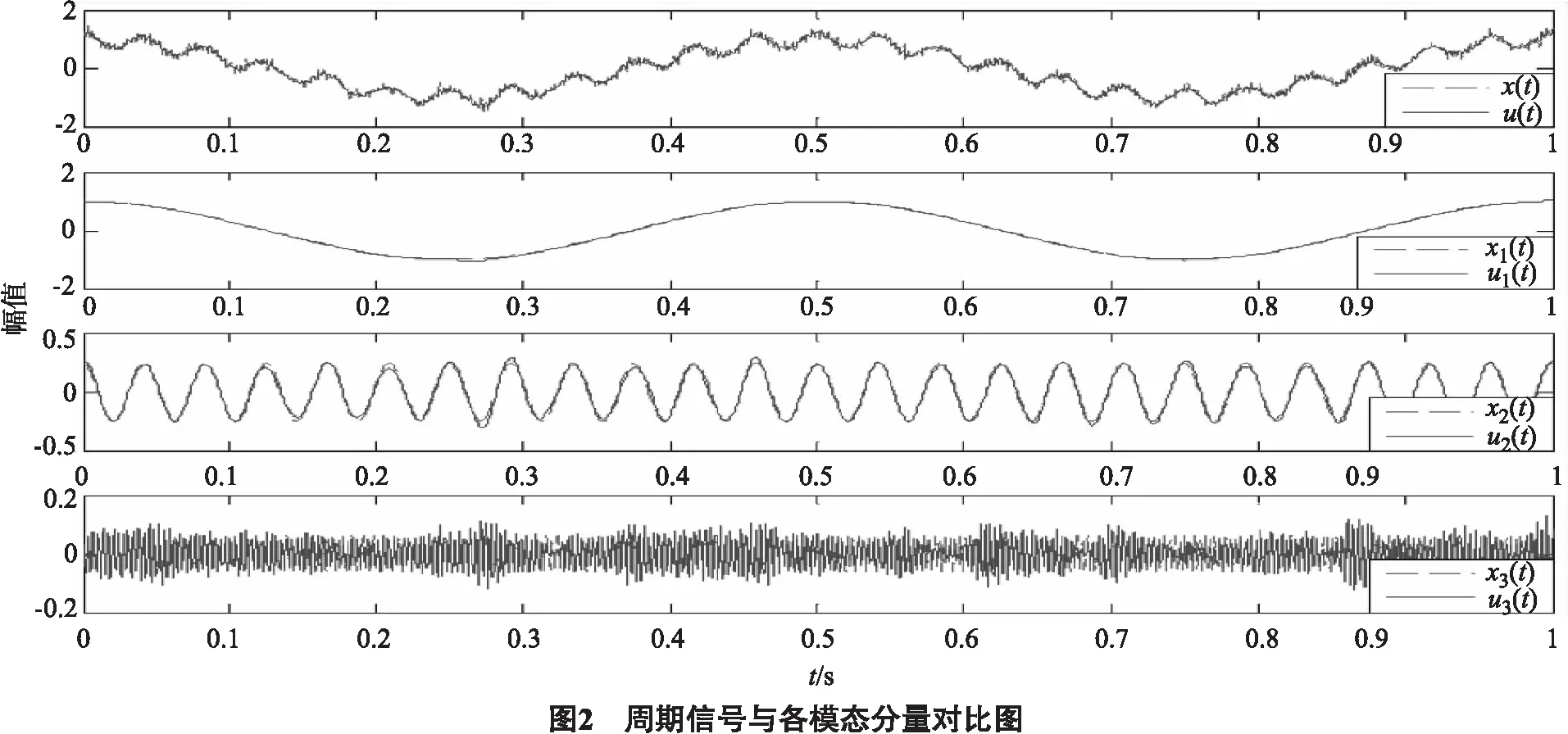
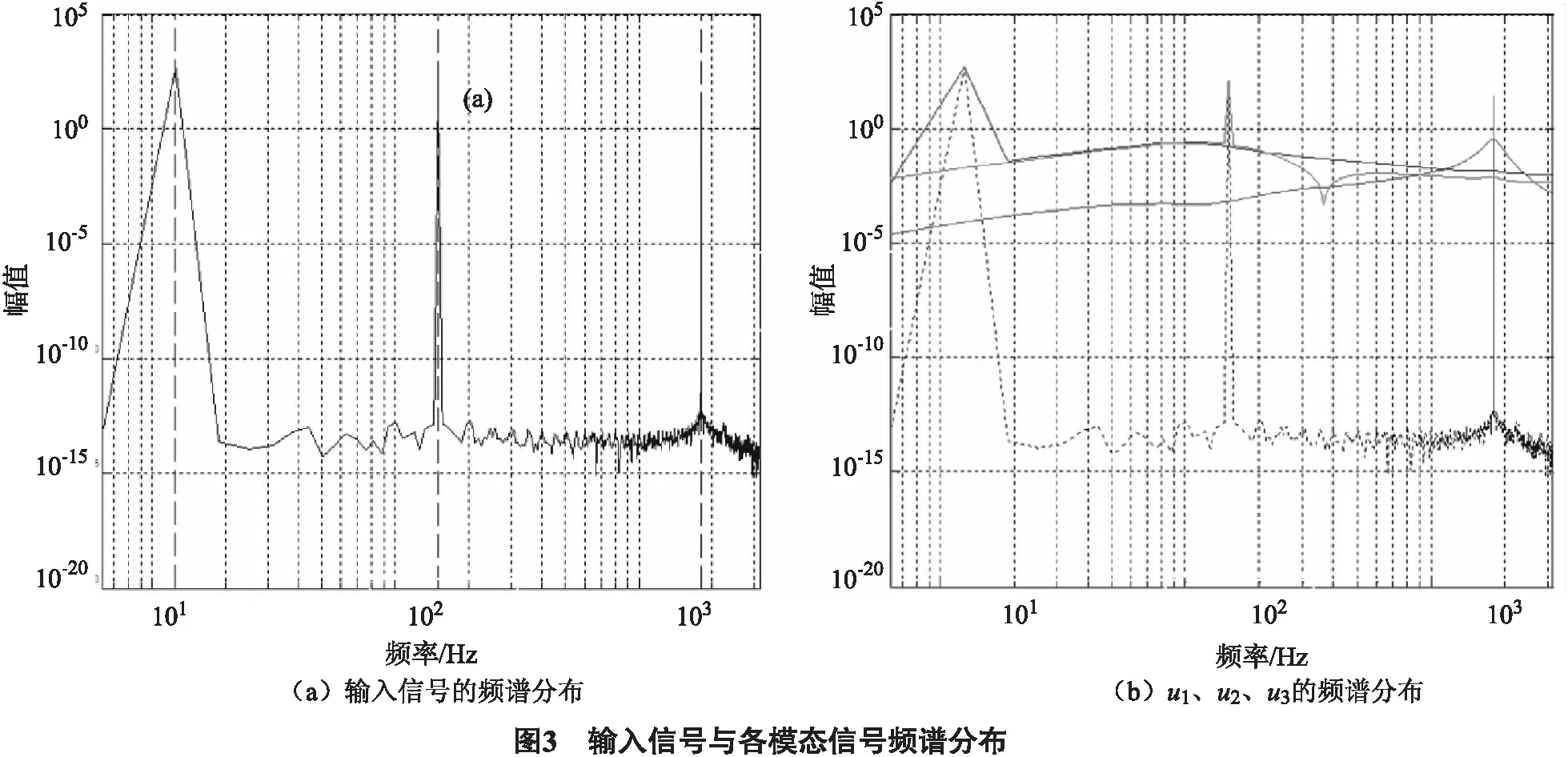
1.3 变分模态分解中各参数分析

1.3.1 模态数对变分模态分解的影响

对信号进行VMD分解时，需要预先给定分解模态数K，因K会影响到信号VMD分解的精度和效果.针对不同的K对周期信号x(t)进行分解，并通过分析信号VMD分解后各IMF与原信号x(t)之间的相关系数ρ，确定“过分解”和“欠分解”现象是否发生.

1) 基于不同K(K=2、3、4、5)值对周期信号x(t)进行VMD分解，结果如图4所示.当K=2时(图4 a)，分解出了288 Hz的余弦信号，而2 Hz与24 Hz的余弦信号却叠加在了一起(“欠分解”)；当K=3时(图4 b)，2 Hz、24 Hz与288 Hz的余弦信号被完全分开；当K=4时(图4 c)，分解出了2、24、288 Hz的余弦信号，分别对应u1(t),u2(t),u4(t)，同时也出现了虚假模态u3(t) (“过分解”)；当K=5时(图4 d)，分解出了2、24、288 Hz的余弦信号，分别对应u1(t),u2(t),u4(t)，同时也出现了虚假模态u3(t),u5(t) (“过分解”).

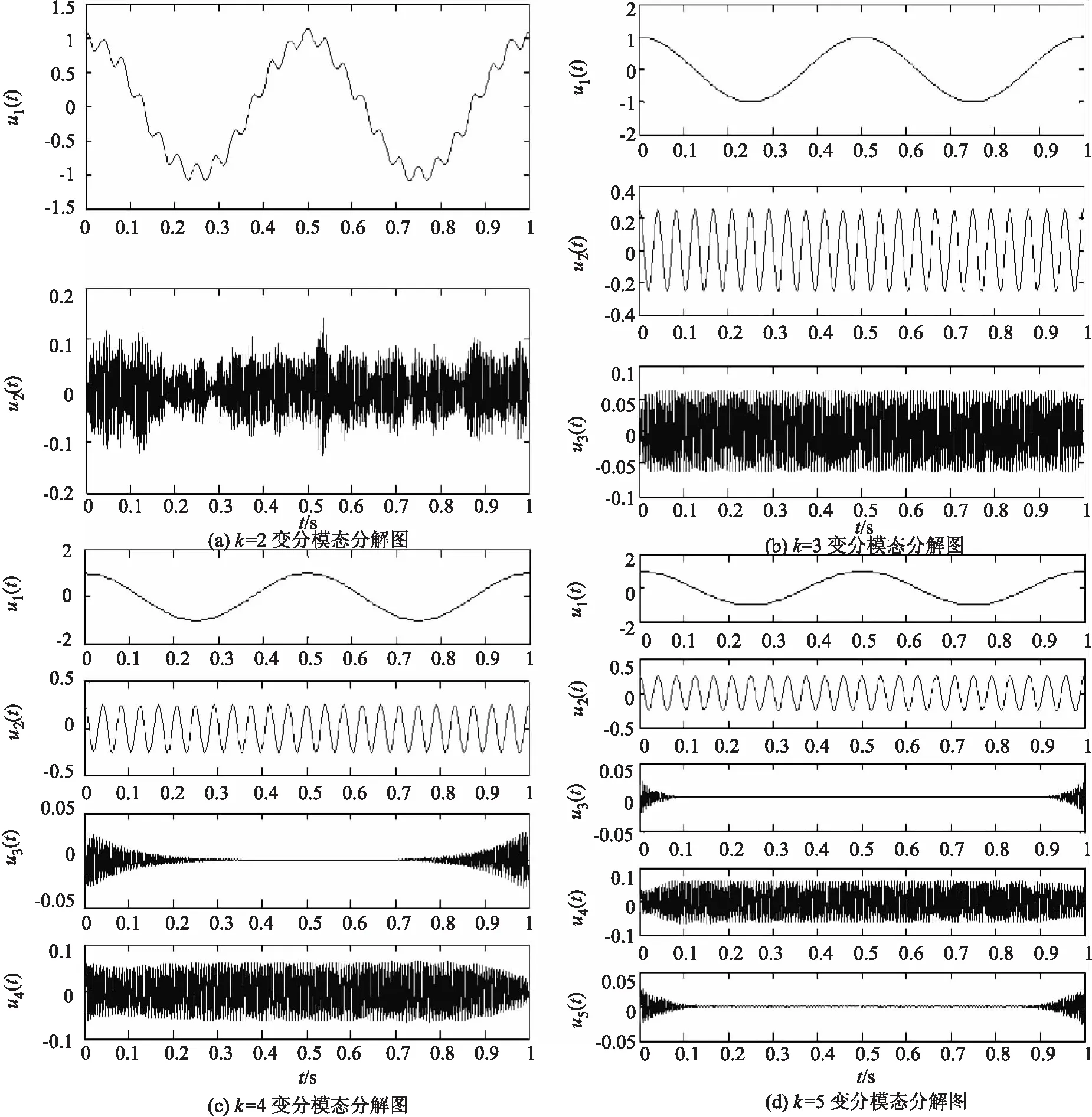
图4 K=2,3,4,5; α=2 000时，周期信号变分模态分解图

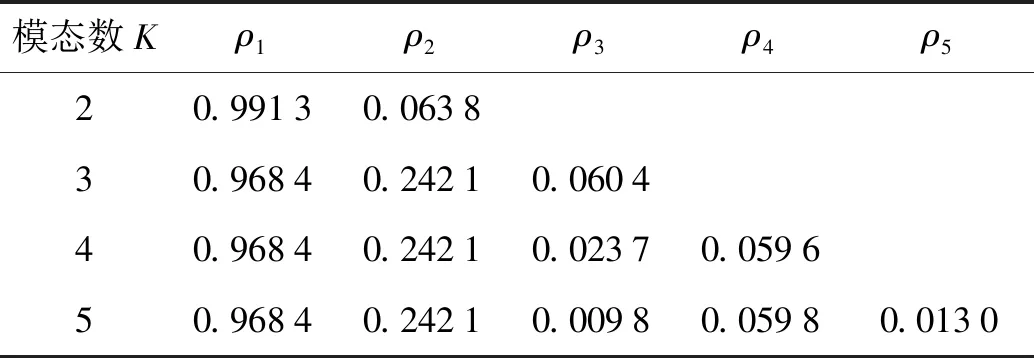
表1 不同K值下VMD分解后各模态与x(t)之间的相关系数

2) 基于不同K(K=2、3、4、5)值对周期信号进行VMD分解并记录分解后各IMF与原信号之间的相关系数ρ，结果如表1所示.当K=4时，模态u3与原信号之间的相关系数ρ3=0.023 7；当K=5时，模态u3,u5与原信号之间的相关系数ρ3=0.009 8,ρ5=0.013 0，出现了虚假模态.

1.3.2 平衡约束参数对变分模态分解的影响

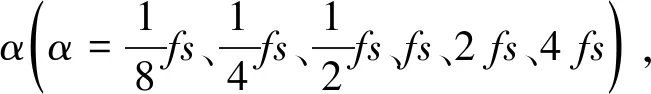
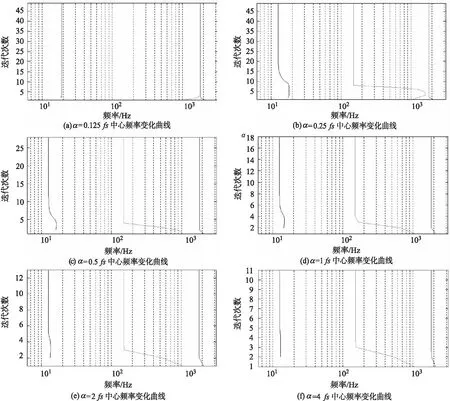
图5 不同α值下信号中心频率变化曲线

2 自适应变分模态分解

通过对周期信号x(t)在不同K和α值的分析得出：K过小，VMD会出现“欠分解”现象；K过大，则会出现“过分解”现象；α越小，IMF带宽越大，容易出现中心频率重叠及“欠分解”现象，α越大，IMF带宽越小，中心频率重叠及“欠分解”现象消失，但计算量增大.基于以上分析，一般取α=1fs，并提出自适应变分模态分解法(AVMD)，该方法的具体步骤如下.

1)初始化ρ0,K=2,平衡约束参数α=1fs;

2)对信号进行VMD分解,计算每一个IMF与原始信号的相关系数ρ;

3)判断ρi,ρ0之间的关系,若ρi<ρ0,则停止分解;否则增加模态数,继续分解,直到满足停止条件;

4)存储最优K值,输出IMF.

2.1 自适应变分模态分解性能分析

1)正交性性能分析

Huang等人在经验模式分解(EMD)中利用连续函数空间C[a,b]的内积定义了所有IMF分量的整体正交性指标IO，如(15)所示.

(15)

对任意两个IMF分量的正交性指标IOi,j定义为(16).

(16)

IO表征了各IMF分量之间的正交性，IO越小越好；当IO=0时，各IMF分量间完全正交.对周期仿真信号x(t)分别进行EMD,LMD,AVMD分解，并计算分解后各IMF的整体正交性指标，结果如表2所示.当选择AVMD时，IO=1.738 9×10-4，远小于其它分解后得到的IO值，这表明AVMD分解得到的IMF的整体正交性是最好的.

表2 EMD、LMD、AVMD的正交性指标值比较

2)能量保存度分析

能量保存度(IEC)用于对各IMF分量的正交性能进行评判，值越接近于1，能量泄漏越小，IEC的计算公式如(式17)所示.

(17)

式中，ci(t)为分解后得到的第i个IMF分量，rn(t)为趋势项.

表3 EMD、LMD、AVMD的“IEC” 值比较

对周期信号x(t)分别进行EMD,LMD,AVMD分解，计算每种分解后能量保存度，结果如表3所示.当选择AVMD时，IEC=0.985 1，大于其它分解方法得到的IEC值，这表明AVMD分解后得能量泄漏最小.

2.2 基于自适应变分模态分解的佤语孤立词共振峰估计

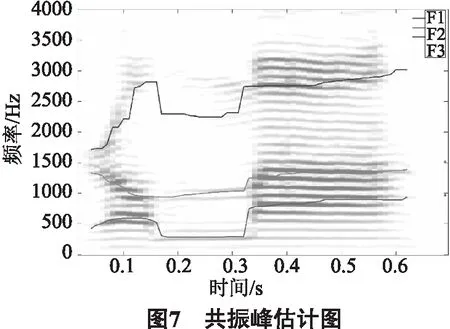
从语料库中选取500个佤语孤立词，每一个音节读8遍，共计4 000条佤语语音.每一条语音的采样频率为8 000 Hz，帧长320、帧移80，加汉明窗，窗宽为帧长的1/4，分别对每一条语音进行分帧、加窗、预加重处理.预加重的目的是降低基频对共振峰检测的干扰.然后利用AVMD分解，由于缺少标准佤语共振峰频率标注语料库，最终选择将所求结果与Praat提取的共振峰频率做比对，若以Praat提取的共振峰频率为标准，则平均正确率可达85.50%，其中的一个共振峰提取图如图7.

3 结语

通过对VMD的两影响参数：分解模态数K、平衡约束参数α进行分析，并从基于K和α的相关系数ρ、中心频率变换值、IO值等参数的变换结果，提出了自适应变分模态分解法(AVMD).通过对本征模态函数的正交性能、能量保存度2个方面验证了该方法的可行性，并利用该方法成功提取到了佤语孤立词的前3个共振峰频率，实现了对佤语共振峰的估计，平均正确率达到85.50%.由于变分模态分解在处理语音信号时，存在端点效应，在接下来的工作中，如何消除端点效应对语音信号的影响是进行下一步实验的研究重点.