启动压力梯度对致密油藏水平井裂缝参数的影响

林 旺，范洪富，车树芹，王少军，闫 林，陈福利

(1.中国地质大学(北京)能源学院，北京 100083；2.中国石油勘探开发研究院，北京 100083)

0 引 言

致密油藏成为目前产量接替的新储量[1-2]，致密油藏由于其极低的流动能力，常规直井难以进行开采，目前以水平井规模压裂的方式进行开采[3-5]。致密油藏水平井多段压裂后形成多条横向裂缝，形成储层基质与人工裂缝两种介质，这两种介质的物性参数差异很大，基质渗透率极小，在0.1 mD以下，而人工裂缝中的渗透率却往往在100 mD以上。流体在两种介质中的流动规律不同，在基质中流体渗流能力很差，存在很大的启动压力梯度[6-7]，需要克服一定的渗流阻力才能流动，为低速非达西渗流。整个系统渗流过程复杂，致密油藏压裂水平井开发的产能预测出现了新难度，开发动态规律认识不清楚，目前对于压裂水平井开发的试井与产能研究很多，大多数运用位势理论的压降叠加原理，以点汇或线汇的渗流规律为基础进行产能公式推导[8-10]，难以考虑启动压力梯度等非线性渗流特征，对启动压力梯度在开发动态规律及裂缝参数优化中的影响也没有清晰的认识。本文在前人对压裂水平井开发渗流模型的基础上，综合考虑致密油藏中启动压力梯度的影响，建立了致密油藏压裂水平井考虑启动压力梯度的产能模型，并在此基础上研究了启动压力梯度对流动阶段的划分、裂缝参数优化的影响进行了研究，为致密油藏的有效开发提供了理论与技术的支持。

1 致密油藏压裂水平井产能模型

假定盒状油藏中间一口水平井，沿水平井分布多条横向裂缝，裂缝与水平井垂直，水平井只在与裂缝交叉的地方射孔，流体从基质流向裂缝，再经由裂缝流向井筒，忽略井筒的压力损失；流体微可压缩，渗流为油相单相等温渗流。

1.1 控制方程

基质中的流动为考虑启动压力梯度的低速非达西流动，其运动方程见式(1)。

(1)

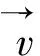
而在裂缝中为达西线性渗流，其运动方程见式(2)。

(2)

由于基质水平渗透率与垂直渗透率往往差异较大，忽略基质中流体的垂直流动，简化为XY平面二维流动，结合基质连续性方程及岩石与流体的状态方程，可以得到基质的控制方程，见式(3)。

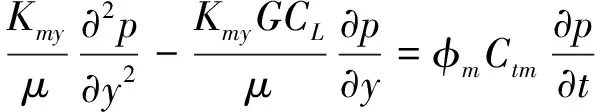
(3)

式中：Kmx为基质在X方向的渗透率，μm2；Kmy为基质在Y方向的渗透率，μm2；CL为流体压缩系数，MPa-1；Ctm为基质综合压缩系数，MPa-1；φm为基质孔隙度，f。

裂缝宽度很小，流体在裂缝中沿着裂缝面流动，忽略裂缝中流体沿X方向的流动，简化为了YZ平面二维流动，并加入流体从裂缝流入井筒而形成的源汇项，同时由于没有考虑X方向的渗流，需要加入流体从基质向裂缝的流入项，可以得到裂缝的控制方程，见式(4)。

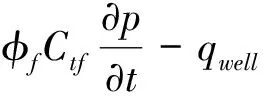
(4)

式中：Kfy为裂缝在Y方向的渗透率，μm2；Kfz为基质在Z方向的渗透率，μm2；Ctf为裂缝综合压缩系数，MPa-1；φf为裂缝孔隙度，f；qmf为单元网格从基质流向裂缝的流量，cm3；qwell为裂缝向井筒的流量，cm3。

1.2 模型求解

考虑到裂缝分布的复杂性及裂缝与基质两种介质的渗流规律的差异，用解析的方法难以得到精确的解，本文以有限体积的方法进行求解。将基质与裂缝两种介质统一划分网格，基质采用非结构化网格，而裂缝采用长条形网格，如图1所示。非结构网格能很好地模拟储层的各种复杂的形态，利于边界调节及裂缝与基质衔接的实现，便于控制网格密度，适应性较强，网格生成有众多富有成效的方法和自适应技术。

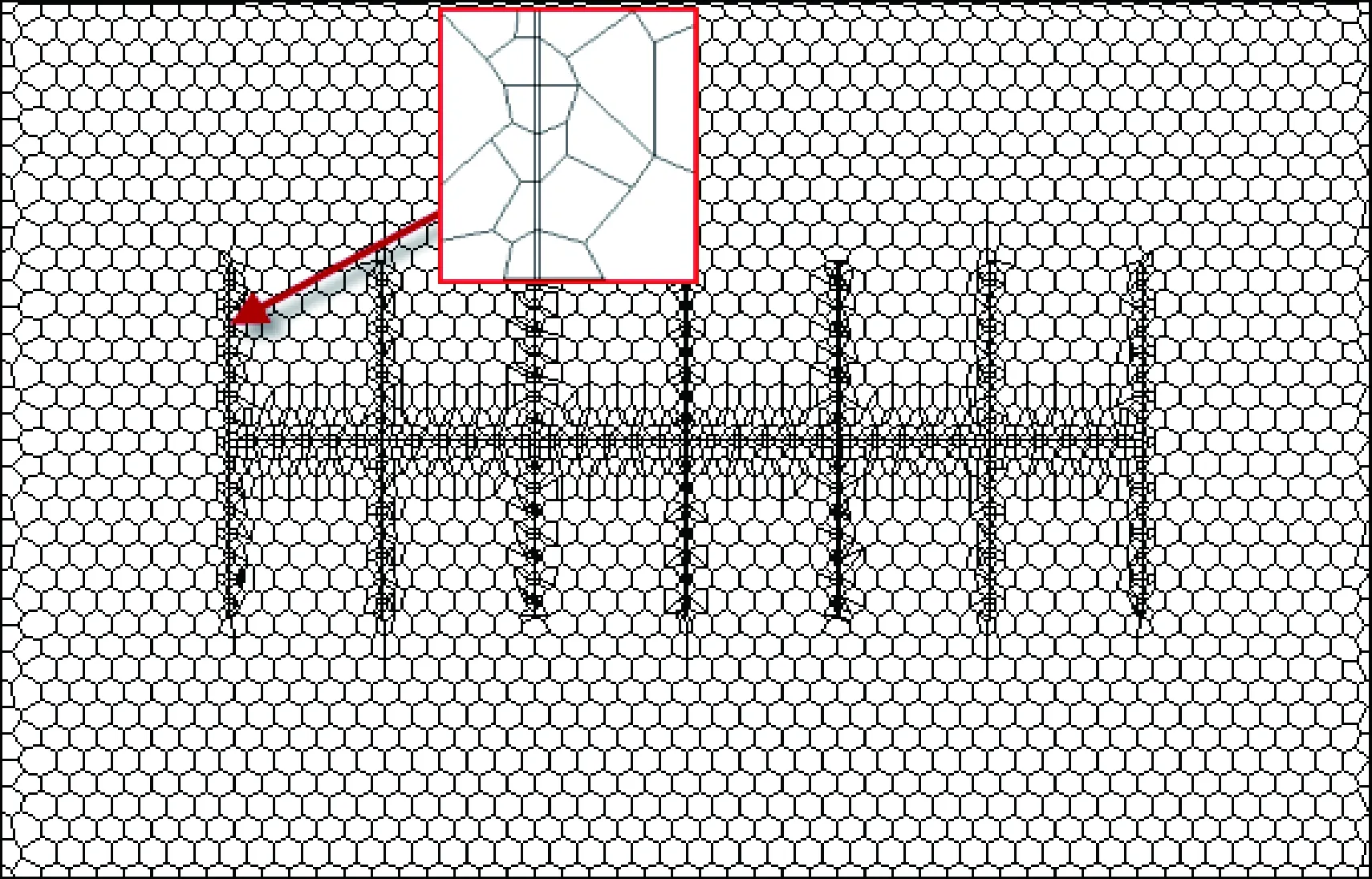
图1 基质与裂缝网格划分示例图Fig.1 Material and fracture grid

采用块中心的形式，在基质与裂缝所在的网格上分别对基质与裂缝控制方程对单元控制体积与时间进行积分。

为进一步提高作者网上投稿的稳定性、可靠性、安全性，为便于读者与编辑部的联系、交流，《中国石油大学胜利学院学报》编辑部已于2013年5月1日启用新邮箱slxb＠sohu.com，原邮箱slxueb＠yahoo.com.cn自2013年8月19日停用。欢迎广大作者、读者通过新的电子邮箱与本刊联系。感谢您的理解与支持！

对基质系统见式(5)。

(5)

对裂缝系统见式(6)。

(6)

应用Gauss定理，可以将左边的体积分改成沿网格侧面的面积分，时间积分采用显示格式进行离散，简化整理得到对基质系统和对裂缝系统，分别见式(7)和式(8)。

(7)

(8)

对每个网格动用以上的离散格式，联立并使用迭代的方法进行求解。

1.3 模型验证

为了验证模型与求解的正确性，将本模型应用于长庆油田典型致密油井YP4。该井所在储层平均孔隙度10.3%，渗透率0.4 mD，地层压力16.6 MPa，原油黏度1.7 mPa·s，饱和压力10.79 MPa，分成11段进行大规模压裂，生产过程由于各种原因改变过工作制度，主要以略低于饱和压力的9 MPa作为井底流压进行生产。利用本文建立的模型进行计算，并与实际生产数据进行比较，如图2所示，可以看出计算结果与实际生产数据基本符合，证明本文所建模型可以用于生产实际。

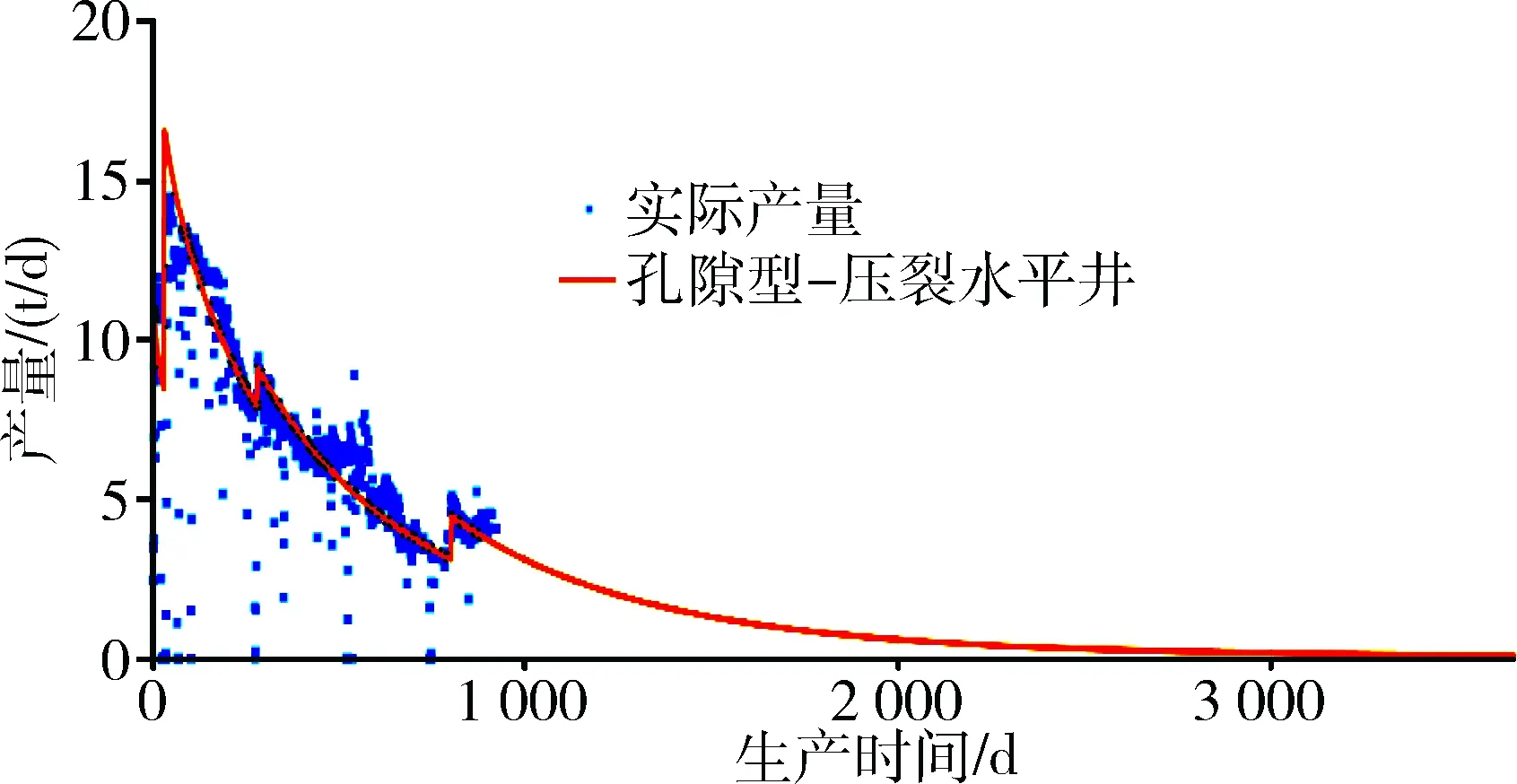
图2 YP4井计算结果与实际生产数据比较图Fig.2 YP4 calculated results and real production data

2 开发动态分析

典型致密油藏的产油量与累积产油量的关系曲线如图3所示。压裂水平井开发阶段分为第一线性流阶段，裂缝干扰流阶段，第二线性流阶段和拟稳态流动阶段。

在第一线性流阶段，流体从裂缝之间的基质流向裂缝，如图4所示。流动距离短，阻力小，产油量高，而且裂缝之间的干扰还未形成，属于第一稳产阶段，累积产油量增加较快；随着压力波的传播，当相邻两条裂缝之间的压力波相遇形成干扰后，就进入了裂缝干扰流阶段，由于裂缝之间的干扰，裂缝之间基质能量消耗较快，产油量下降加快；当压力波传播到裂缝控制区域(图4中Ⅰ区)之外(图4中Ⅱ区)时，流体从Ⅱ区流向Ⅰ区，为第二线性流阶段，由于Ⅱ区能量充足，能够保持一个较为稳定的产油量，为第二稳产阶段；当压力波传播到Ⅱ区边界后，如果是封闭边界，则进入了边界流阶段，没有能量补充，产油量迅速下降。

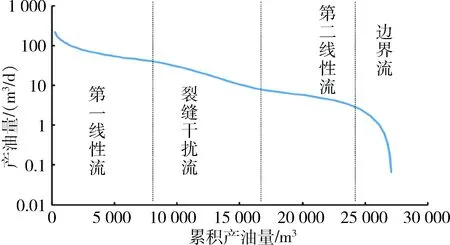
图3 致密油藏压裂水平井典型产量曲线Fig.3 Classic production curve of tight oil reservoirsfractured horizontal well

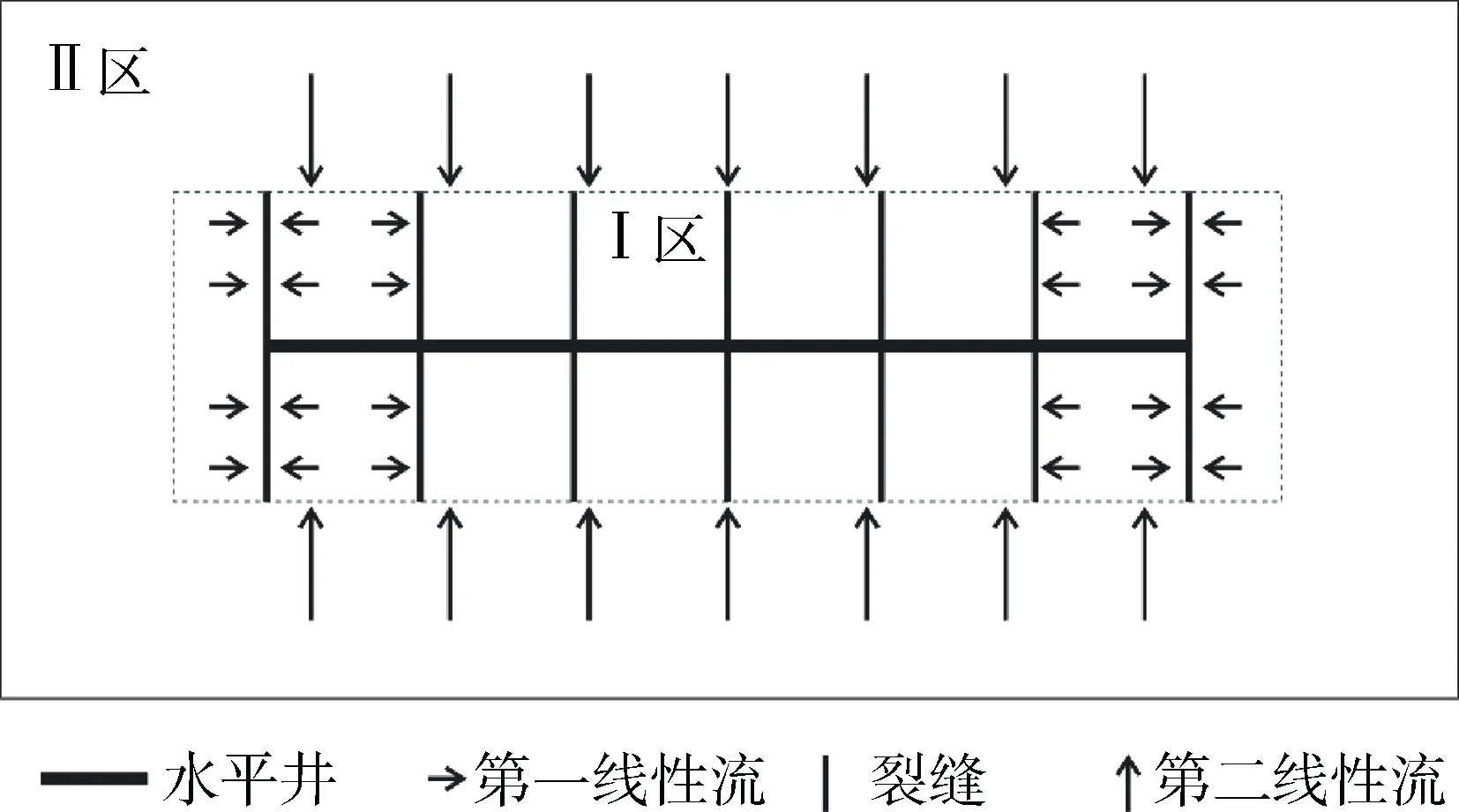
图4 致密油藏流体流动示意图Fig.4 Schematic diagram of fluid flow in tight oilreservoirs with fractured horizontal well

国内外很多学者都认为，压裂水平井的开发可以分为第一线性流阶段、第一径向流阶段、第二线性流阶段和第二径向流阶段[11-14]。但本文的研究成果表明，第一径向流阶段很难出现，除非裂缝长度非常短，而目前致密油藏的开发以大规模压裂为主，难以见到第一径向流阶段；同样地，压裂水平井小井距开发是目前致密油藏提高采收率一种有效手段，也难以见到第二径向流阶段，在第二线性流阶段后，压力传播很快到达边界，形成边界流，产油量极速下降。

3 启动压力梯度对开发动态的影响

3.1 对流动阶段划分的影响

致密油藏渗透率极低，流体渗流为低速非达西渗流，因此，用来描述低速非达西渗流的启动压力梯度对致密油藏的开发动态及流动阶段划分有很大的影响。为了研究启动压力梯度对致密油藏压裂水平井开发动态的影响，以1 500 m×1 000 m×3.8 m大小的盒状油藏为研究对像，水平井长度为1 000 m，居于油藏中心，沿水平井均匀分布7条裂缝，裂缝长度相同，均为400 m，油藏原始压力16.5 MPa，以2 MPa的井底流压定压生产。

启动压力梯度对开发动态影响规律如5图所示。随着启动压力梯度的增加，该压裂水平井能够采出的累积产油量越来越小，滞留在基质中的剩余储量越来越大。同时，随着启动压力梯度的增加，压裂水平井开发的流动阶段变得越来越模糊。从图5可以看出，当不考虑启动压力梯度时，可以明显地划分出第一线性流、裂缝干扰流、第二线性流和边界流四个阶段，随着启动压力梯度的增加，第一线性流与第二线性流的长度在缩短，当启动压力梯度增加到0.4 MPa/m时，第一线性流与第二线性流的稳产阶段几乎消失不见，提前进入了边界流动的快速递减阶段。

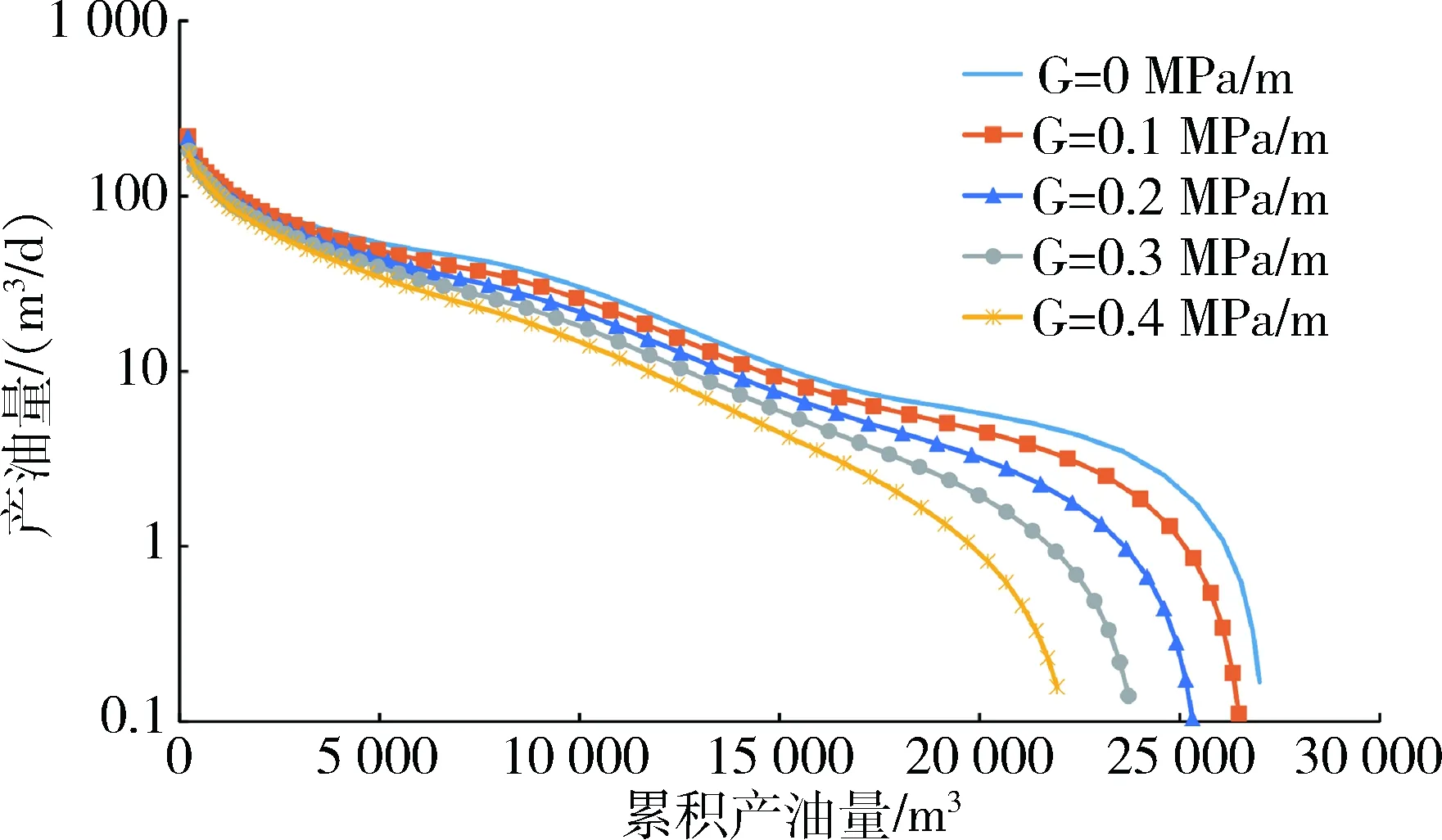
图5 启动压力梯度对致密油藏水平井开发动态的影响Fig.5 Effect of start-up pressure gradient on tight oilreservoirs with fractured horizontal well

3.2 对裂缝参数优化的影响

致密油藏由于渗透率极低，注水开发难以形成有效的驱替压力，目前基本上以衰竭式开发为主，需要进行大规模的压力，形成贯穿水平井的多条横向裂缝，依靠裂缝沟通储层中的流体，因此裂缝的主要参数，包括裂缝条数和裂缝半长，对致密油藏压裂水平井的开发效果有着重要的影响，裂缝条数越多，裂缝越长，累积产油量也多，但形成更多、更长的裂缝需要进行更为复杂的压裂施工，所需成本越高，因此需要对裂缝参数进行优化设计，以达到开发效果与成本的最优化。

致密油藏由于极低的渗透率及由此而产生的启动压力梯度对裂缝参数的优化具有很大的影响，为了研究启动压力梯度对致密油藏压裂水平井裂缝参数优化的影响，以某典型致密油藏为例，分别计算了在不同的启动压力梯度下，裂缝半长、裂缝条数对最终累积产油量的影响。该研究区块的储层渗透率为0.16 mD，孔隙度9%，油藏压力165 MPa，原始溶解气油比为98.05 m3/m3，油藏条件下的原油黏度为0.68 mPa·s，假定一个大小为1 500 m×1 000 m×3.8 m的盒状油藏，中心一口长度为1 000 m的水平井，沿着水平井进行多段压裂，形成多条以水平井为对称轴的对称横向裂缝，利用本文建立的模型及求解方法，分别计算不同的启动压力梯度条件下，不同的裂缝半长和不同的裂缝条数在生产到废弃产量为0.1 m3/d时的累积产油量，对比分析最优的裂缝参数。

研究结果表明，启动压力梯度对裂缝半长、裂缝条数优化的影响具有相似的规律，如图6所示。不考虑启动压力梯度时，最终累积产油量与裂缝参数相关性不大，启动压力梯度越大，裂缝半长和裂缝条数对最终累积产油量的影响越大。在不考虑储层启动压力梯度的条件下，以衰竭式进行开发的压裂水平井，裂缝半长、裂缝条数对最终的累积产油量影响不大，这是因为衰竭式开发的驱动力为流体及岩石的弹性膨胀，根据物质平衡原理，其最终累积产油量只与流体、岩石的膨胀性及储层的生产压差有关。但随着启动压力梯度的增加，致密油藏流体渗流还需要克服额外的阻力，在生产压差不变的条件下，单条裂缝控制的泄流半径缩小，需要更长、更多的裂缝，因此，存在启动压力梯度的致密油藏中，水平井压裂开发需要对裂缝半长和裂缝条数进行优化，充分考虑启动压力梯度的影响。

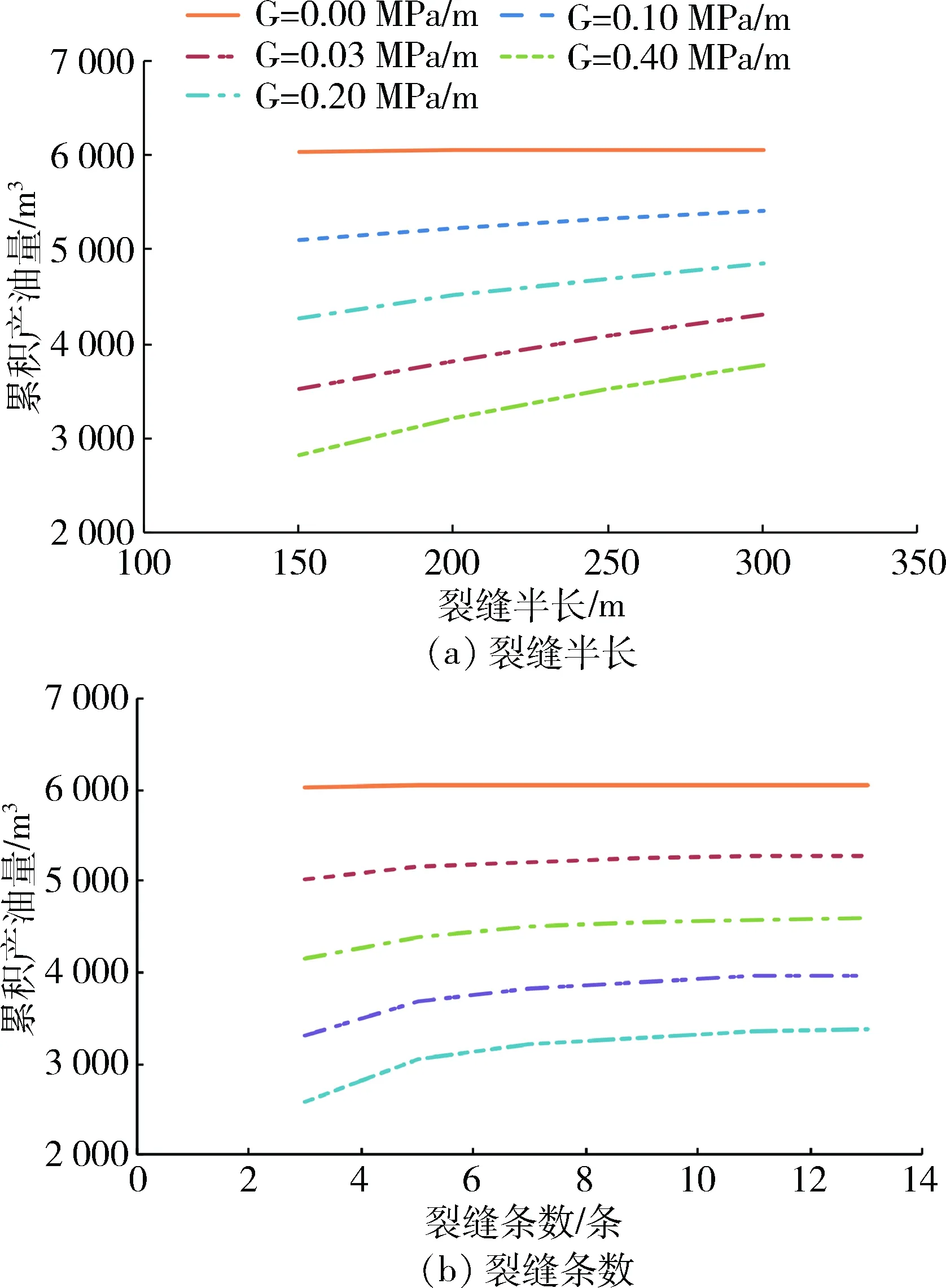
图6 不同启动压力梯度下裂缝参数对累积产油量的影响Fig.6 Effect of fracture parameters on cumulativeproduction of different start-up pressure gradient

具体到油田实际，当启动压力梯度从0 MPa/m变化到0.4 MPa/m时，分别计算裂缝半长为150 m、200 m、250 m、300 m的累积产油量，计算结果如图6(a)所示。在不考虑启动压力梯度时，累积产油量与裂缝半长的变化很小，当裂缝长度从150 m增加到300 m时，累积产油量从6 041.9 m3增加到6 056.3 m3，只增加了约14 m3；当启动压力梯度为0.1 MPa/m时，裂缝半长从150 m增加到300 m时，累积产油量从5 099.8 m3增加到5 403.1 m3，增加了303.3 m3，增幅为5.9%；当启动压力梯度增加到0.2 MPa/m时，累积产油量随着裂缝半长的增加从4 275.8 m3增加到4 849.5 m3，增加了573.7 m3，增幅为13.4%；当启动压力梯度增加到0.4 MPa/m时，累积产油量从2 817.5 m3增加到3 784.4 m3，增加了966.9 m3，增幅为34.3%，可以看出，启动压力梯度越大，累积产油量对裂缝半长越敏感，对裂缝半长的选取越重要，如图7(a)所示，在启动压力梯度为0.4 MPa时，当裂缝半长从150 m增加到200 m时，累积产油量增加了390.7 m3，增幅为13.9%；当裂缝从200 m增加到250 m时，累积产油量增加320.7 m3，增幅为10%，当裂缝从450 m增加到500 m条时，累积产油量只增加了23.5 m3，增幅为0.6%，因此本研究区块在启动压力梯度为0.4 MPa/m时的最优裂缝半长为400 m。

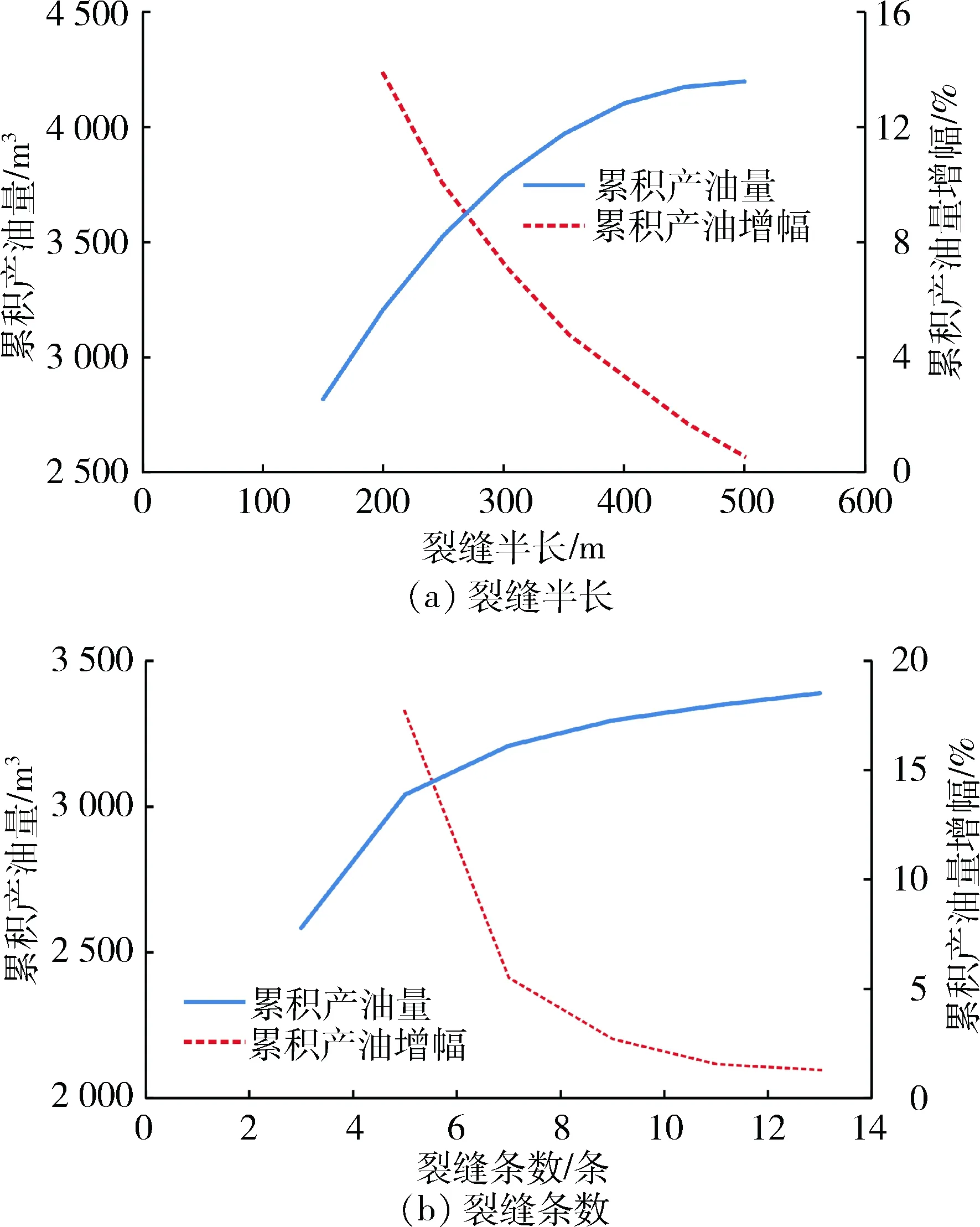
图7 启动压力梯度对裂缝参数优化的影响Fig.7 Effect of start-up pressure gradient onfracture parameters optimization

相似地，当启动压力梯度从0 MPa/m变化到0.4 MPa/m时，裂缝条数从3条增加到13条的累积产油量，计算结果如图6(b)所示。当不考虑启动压力梯度时，累积产油量随着裂缝条数的增加只有微小的增加，而当启动压力梯度增加到0.1 MPa/m时，累积产油量从5 031.3 m3增加到5 276 m3，增加了244.7 m3，增幅为4.9%；当启动压力梯度为0.4 MPa/m时，累积产油量随着裂缝条数从3条增加到13条时从2 583.4 m3增加到3 389.7 m3，增加了806.2 m3，增幅为31.2%，裂缝条数对累积产油量的影响越大；同时，累积产油量随着裂缝条数的增加而增加，但增加的幅度越来越小，如图7(b)所示，在启动压力梯度为0.4 MPa时，当裂缝条数从3条增加到5条时，累积产油量增加了457.5 m3，增幅为17.7%；当裂缝从5条增加到7条时，累积产油量增加167.4 m3，增幅为5.5%，当裂缝从11条增加到13条时，累积产油量只增加了22.1 m3，增幅为0.6%，因此存在最优的裂缝条数，需要根据储层地质参数及启动压力梯度综合考虑，本研究区块在启动压力梯度为0.4 MPa/m时的最优裂缝条数为9条。

4 结 语

通过建立并求解致密油藏压裂水平井开发的渗流模型，得到了致密油藏压裂水平井开发动态规律，将整个开发过程分为第一线性流、裂缝干扰流、第二线性流和边界控制流四个阶段；启动压力梯度对压裂水平井开发动态规律影响明显，随着启动压力梯度的增加，第一线性流、第二线性流的稳产阶段缩短，提前进入快速递减阶段；同时，启动压力梯度对致密油藏压裂水平井开发裂缝参数优化具有显著的影响，启动压力梯度越大，裂缝参数对累积产油量的影响越大，但变化的幅度越来越小，存在最优的裂缝半长与裂缝条数，对于研究的某典型区块来说，在启动压力梯度为0.4 MPa/m时，最优的裂缝半长为400 m，裂缝条数为9条。