基于九域图的变电站无功优化改进控制策略研究

高梓维，王存旭

（沈阳工程学院a.研究生部；b.自动化学院，辽宁 沈阳 110136）

电压质量作为衡量电能质量的基础指标，其大小波动以及稳定性直接影响到整个系统运行的安全，如若不及时调控，会造成电网大停电事故。无功优化可以有效减少电能损耗，提高电气设备的使用寿命［1］。引起电压损耗与电网损耗所占比重最大的因素是无功功率。因此，区域电网应采用分层分区、就地平衡的原则来调整。从长期的研究中发现，通过采用实时调整电量的无功电压优化控制技术，在保障系统守恒原则的基础上，同时兼顾了电能质量与安全要求。

目前，在无功控制策略研究领域中，主要有离线优化和实时监控两种。实时监控是指九域图及其改进的无功电压控制策略。文献［2］分析了基于九域图的无功电压控制方法的优点及其在电压无功控制中的应用和实现方法。文献［3］阐述了改进后的九域图及其详细控制策略。文献［4］分析了基于模糊边界无功准则的控制策略的特点，并讨论了考虑高压侧跨越电压极限的无功电压控制策略。

基于传统九域图的无功电压控制策略及其改进方案存在以下问题：

1）频繁的设备动作导致开关设备容易断裂［5-6］；

2）不能考虑变电站的高压侧［7］。

因此，它不是一种经济高效的控制策略。如果负荷预测的准确性不高，或者由于供电系统当天有突然的负荷，即负荷波动较大，实际负荷与预测负荷有很大差别，则基于负荷预测的无功控制策略不能满足电压调整的要求［8］。

本文结合了离线优化和实时监控两者的优缺点，提出了一种基于空间九域图的变电站无功电压控制策略。在负荷预测的基础上，对变电区域进行全局无功优化。通过建立基于负荷预测的全局无功优化模型，得到配电网中各变电站的预期调整方案，将一天划分为若干个时区，并根据优化曲线获得各时区的运行边界。空间九域图的时域划分，确定了各时区九域图电压调节的边界条件，避免了电容器组和有载变压器分接头在非理性区域的频繁切换和传输，并通过变电站案例确定无功调整方案，借此为实现电网运行的安全稳定提供了实效的技术支持以及保障。

1 无功平衡与电压调整原理

无功平衡与电压的关系如图1所示。

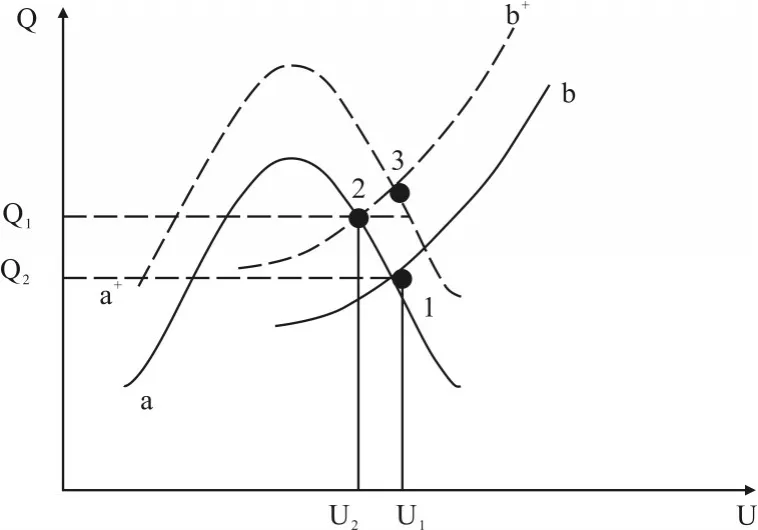
图1 无功电压平衡曲线

图1中曲线a表示电源的无功电压特性曲线，曲线b表示负荷的无功电压特性曲线。其中U1由交汇点1决定，电压在U1点时可以达到无功功率平衡。随着负荷增加，可以用曲线b′来表示其特性。而在同一时刻，若系统无功电源储备未增加，其特性分布曲线仍由曲线a表示，在曲线a与负荷增多的曲线b′交点为2点时，获得了新的平衡点b，U2点表示其负荷点电压，由图1可知U2＜U1。由以上分析可知，即负荷增多时，系统电源不满足在U1处的平衡点，需要采用降压的措施来调整，即在较低的电压程度达到新的平衡。

2 基于负荷预测的全局无功优化方法

1）控制目标

负载是可变的。把当天分为24个时段，通过负荷预测技术可以获得第2天t期的负荷Pt+jQt。有载变压器j的分接头有2Lj+1个齿轮，标记为-Lj,-Lj+1,…,0,1,…,Lj。一般来说每个齿轮是1.25%或2.5%。电容器组h具有容量为mh的电容器Qh。

调整无功功率的方法包括抽头位置Tj和作为自变量的有载变压器j上的电容器组h的开关次数mh。假定所有有载变压器的抽头位置和电容器的开关数都为矢量。

因变量是供电系统的潮流，在变电站的最佳运行条件下有3个目标。第一个目标是最小的网络损失，即f1=minPloss；第二个目标是有载变压器分接头的动作次数X最小；第三个目标是电容器组的开关次数的总和数Y最小。X和Y可以用以下方式表示：

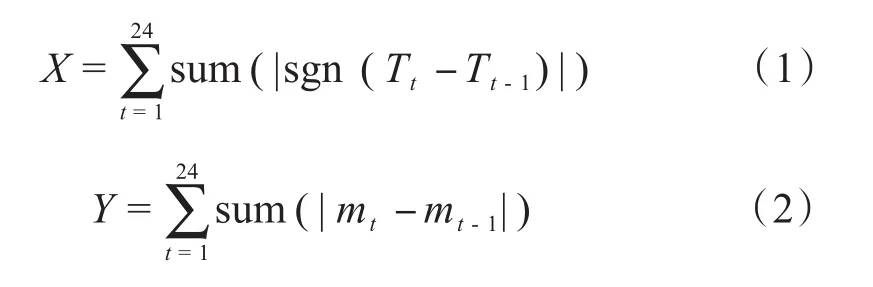
2）约束条件

①潮流平衡约束

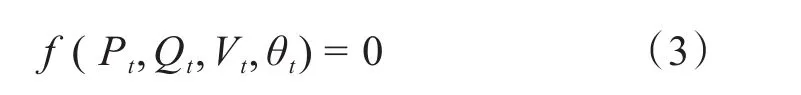
式中，Pt、Qt、Vt、θt分别是n个节点的注入有功功率矢量、注入无功功率矢量、电压幅度矢量、电压相角矢量。

②节点电压约束

式中，Vmin、Vmax分别是n个节点电压幅值向量的下限和上限。

③线路潮流约束

式中，Imin、Imax分别是n个节点的电流幅值向量的下限和上限。

④抽头位置约束

式中，Tmin、Tmax分别是抽头位置的下限和上限。

⑤电容器组数量

式中，mmax是电容器组的最多数量。

3 基于九域图的无功优化控制策略

1）空间九域图

根据变电站低压侧电压上限和下限以及变电站高压侧无功功率的上下限值要求，九域图将操作区域划分为较高无功功率区域和较低无功功率区域，如图2所示。

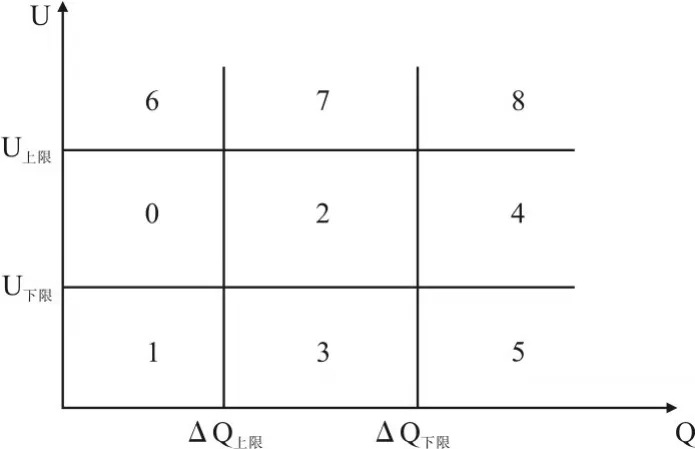
图2 传统九域图

图2中，在0区域，U符合标准，但到达ΔQ上限，故发出切除电容器的命令；在1区域，U到达U下限而ΔQ到达ΔQ上限，故发出先提高电压再切除电容器的指令；在2区域，U与ΔQ均符合标准，故不发出指令；在3区域，U到达U下限，故发出提高电压的指令；在4区域，U符合标准，ΔQ到达ΔQ下限，故发出投入电容器的指示；在5区域，到达U下限与ΔQ下限，故发出先投入电容再提高电压的指令；在6区域，U到达U上限，ΔQ到达ΔQ上限，故发出先切除电容器再降低电压的指令；在7区域，U到达U上限，故发出降压的指示；在8区域，U到达U上限，ΔQ到达ΔQ下限，故发出先降低电压再投入电容器的指令。

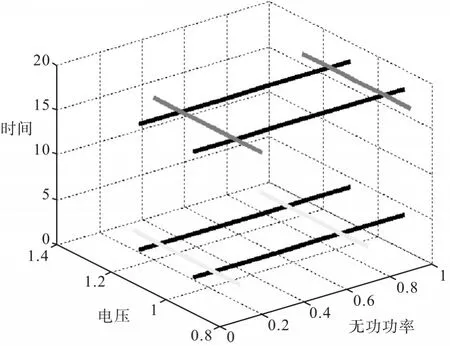
图3 空间九域图

由于不同时刻的负载变化特性及其初始位置不同，传统九域图使用固定无功功率Q和电压U2，必然导致有载变压器和电容器的频繁运行。结合全局无功电压优化模型的优化结果，对九域图的无功功率Q和电压U2边界进行了时间设定。图3为针对传统意义的九域图进行改良，在传统的九域图的基础上，时间轴增加，将Q上下限变成ΔQ上下限，具体如式8所示。

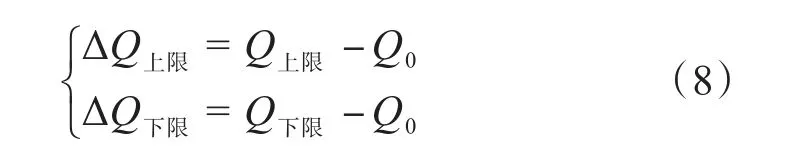
前一时期的上限和下限分别为1.1和0.9，无功功率的上限和下限分别为0.7和0.1；后一时期的上、下电压极限分别为1.1和0.9，无功功率的上限和下限分别为0.9和0.2。在电压调整的过程中遵从就地平衡与集中调控的相互关联，借此用来确定无功功率的基准值Q0。随着Q0的变化，其九域图也随之改变。

2）确定空间九域图的边界

根据全局无功优化方法，得到各时段各变电站的无功调节方案和变电站的低压侧电压变化曲线。基于全局无功优化下的潮流，得到各变电站高压侧无功功率变化曲线。变电站采取无功调节的时期为T1,T2,…,Ts。把一天分为几个时间段，第一个时是Ti-1期间和Ti+1期间的平均值。

根据变电站低压侧电压变化曲线和高压侧无功变化曲线，计算时间周期x中低压侧电压平均值U2和高压侧无功功率Q，分别表示为U2best,x和Qbest,x。因此，可以用式(9)求出每一时段内九域图的电压和无功功率的上限和下限。

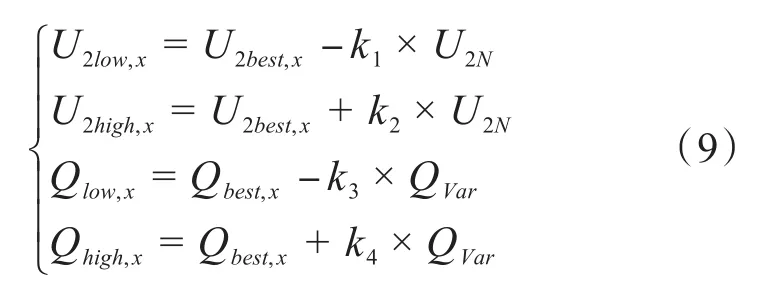
式中，U2N是变电站低压侧的电压；QVar是变电站电容器组的无功补偿容量；k1、k2的取值范围为0.04～0，k3、k4的取值范围为0.3～0.7。

4 算例分析

变电站A、B为区域变电所，维持电力系统功率平衡的点为1点，2点认为注入电压为恒值，故PV节点为节点2。A变电站有9个档位可供调节，B变电站有11个档位可以调节，A、B变电站调节档位均为1.25%。系统配电电路图如图4所示。其中，节点4的全天负荷预测如图5所示。

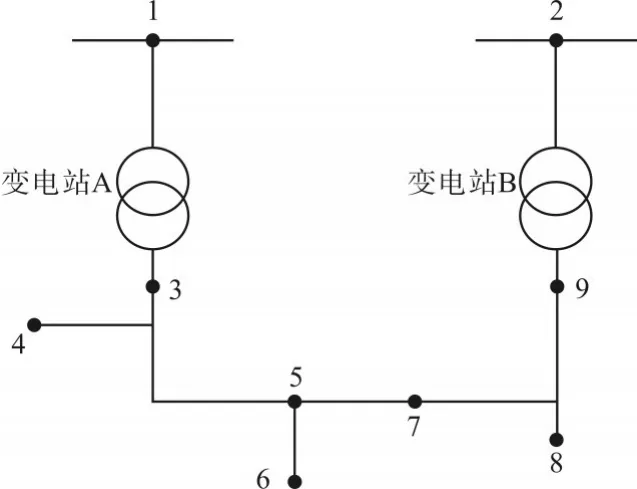
图4 配电系统

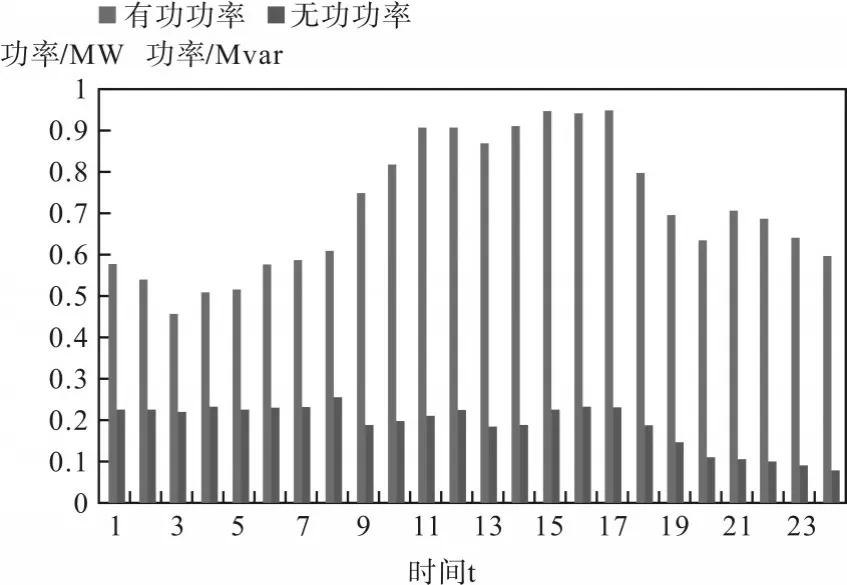
图5 节点4的全天负荷预测

通过求解全局无功优化模型，得到了A、B变电站的期望无功调整方案，如表1和表2所示。

表1 变电站A的预期无功功率调整方案

表2 变电站B的预期无功功率调整方案

在求解全局优化后，图6和图7给出了变电站A、B的低压曲线和高压无功曲线。

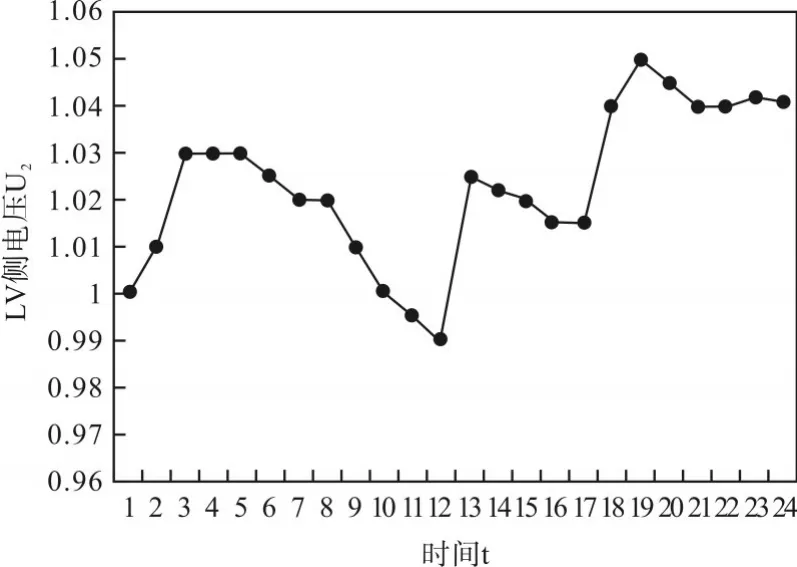
图6 变电站A低压侧变化曲线

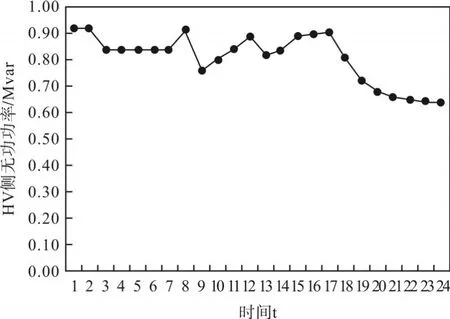
图7 变电站A高压侧变化曲线

在图6、图7中的3、13和20三个时间段内，变电站A实施无功调节方案。因此，空间九域的时间轴被划分为3个部分，即时区（2，8），（9，16）和（16，22）。根据全局无功优化的结果，得到变电站A低压侧电压的变化曲线和高压侧无功功率的变化曲线。

计算每个时区的无功电压边界，取k1=0.03，k2=0.03,k3=0.7,k4=0.7，并获得变电站A的空间九域，如表3所示。

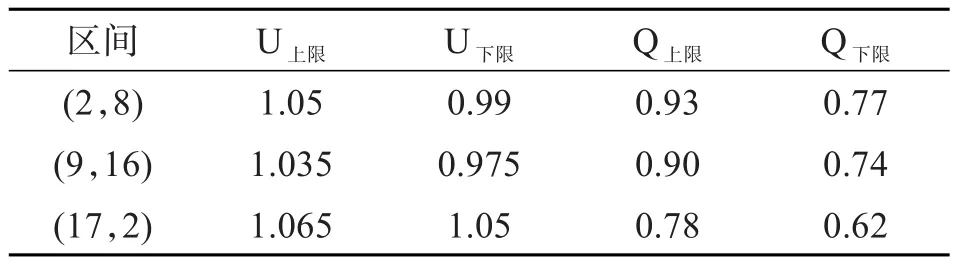
表3 变电站A的空间九域区间

5 结论

本文从无功电压控制现状出发，在传统九域图的基础上，提出了基于空间九域图的变电站无功电压控制策略。针对负荷的变化，一般采用如下两种调控策略：

1）对于负荷的正常范围内的变动，可以结合调整变压器分接头等措施控制电压；

2）对于负荷较大波动的，可采用投切电容器的优化策略。

在不同的时间阶段，九域图的边界是不同的。在负荷预测的基础上，对供电区进行了全局无功优化，得到了空间九域图的时段划分，并确定了各时段九域图电压调节的边界条件。在某种程度上，结合九域图采用协调控制策略，对于整个变配电系统优化无功具有重要意义。