拉力型锚杆锚固段的剪应力解析解

赵 圳

重庆大学 土木工程学院 重庆 400045

1 引言

锚固技术在岩土工程中的发展已经有很长的历史。国内外锚固技术应用已相当成熟，但预应力锚杆锚固机理的研究仍然滞后于实际工程。本文针对压力型锚杆，考虑接触面特性，引入折减系数，理论推导出拉力型锚杆锚固段的剪应力和轴力的数学表达式。

在压力型锚索的锚固理论方面，-学者尤春安[1]的研究结果：

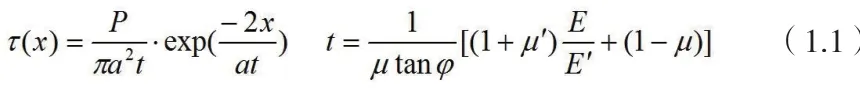
2 理论推导

2.1 基本假定

如图2.1模型，以承载体为原点，沿着锚杆轴向，建一维坐标系，假定：

①锚固体与岩体交界面，满足库伦准则；

②锚固体与岩体均为理想弹塑性材料；

③锚固体横截面上的轴力均匀分布。

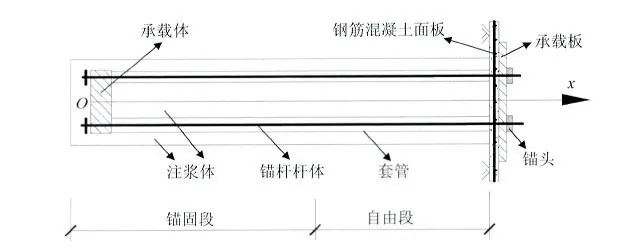
图2 .1 压力型锚杆

图2 .2 锚固段微元体

2.2 推导过程

在锚固段，沿着轴线取一微单元体，如图2.2示，轴向受力平衡，整理得：

考虑库仑定律，可以得：

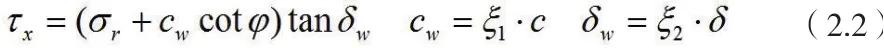
广义胡克定律，锚杆轴向应变：

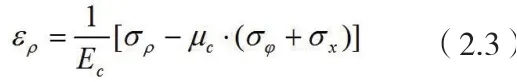
据假设三，可得：

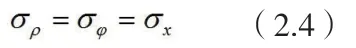
将（2.3）代入（2.4）：

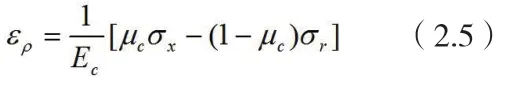
锚杆径向位移[2]：

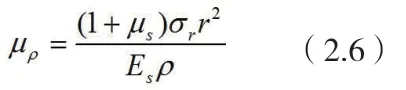
将（2.5）、（2.6）代入（2.7）：

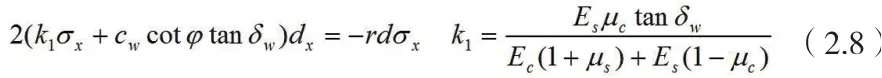
将（2.9）代入（2.8）：

联立（2.3）、（2.6）、（2.10）得压力型锚杆锚固段剪应力和轴力：

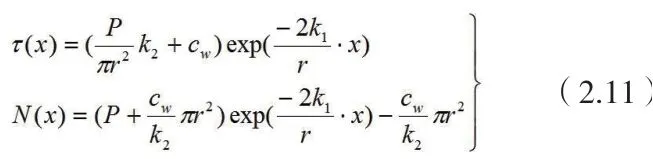
3 计算实例

为验证本文理论，将文献[1]尤安春公式的计算结果，与本文理论的计算结果对比。各项参数文献[1]一致，结果对比见图3.1。

图3 .1 锚固体剪应力分布

从图得：①本文公式的计算结果中，与尤安春公式计算的结果一致，符合实际工程中情况；②剪应力在承载体出最大，随距离增大，呈指数型减小，最后趋于0，符合实际工程情况。

4 结论

①针对压力型锚杆，考虑锚固段锚杆与岩体土体接触面的粘聚力和钻孔注浆的挤压效应，引入折减系数，推导出压力型锚索锚固段剪应力、轴力数学表达式。

②通过实例，本文公式的计算结果中，剪应力和轴力的变化趋势和分布形式与尤安春公式计算的结果一致，符合实际工程。