基于RBF代理模型的调水过程优化研究
高学平,朱洪涛,闫晨丹,孙博闻,张 晨
(天津大学 水利工程仿真与安全国家重点实验室,天津 300350)
1 研究背景
南水北调东线输水干线总长1466.24 km,从江苏省扬州附近的长江干流引水,利用洪泽湖、骆马湖、南四湖、东平湖和沿线的运河、淮河以及周边水库等调蓄工程,采用梯级泵站逐级提水与自流输水结合完成东线调水任务。调蓄工程通过泵站调水的过程中,不仅要充分利用调蓄工程的调蓄能力,还需时刻关注水位的变化,实现安全、稳定调水。武周虎等[1]基于运动波与惯性波传播规律,研究了调水出湖泵站开启的必要和充分时间、出湖泵站开启时间差、湖内水位升高速率。高学平等[2]采用数值模拟的方法,定量描述了相邻梯级泵站开启临界时间差和临界水位。调蓄工程通过控制泵站启闭时间来调节湖内水位,从而不断优化调水过程,其优化过程的通常做法是通过人为不断改变边界条件,利用一维二维耦合水动力模型求解得到时间-水位关系,反复试算并比较各方案结果,得到调水过程较优方案。显然,该方法依赖主观因素,其计算工作量大、效率较低,而且不易得到最优方案。因此,有必要采用智能优化算法进行调水过程优化研究,寻求调水过程最优方案。
目前常用的智能优化算法有遗传算法、粒子群算法、模拟退火算法、神经网络算法等。粒子群优化算法因其运行速度快、结构简单、易于实现,很好地解决了非线性、全局优化等复杂问题,在调水工程中取得了广泛的应用[3-5],郭旭宁等[4]、丁咏梅等[5]均采用粒子群优化算法求解优化调度模型,实现水量的优化调度。调蓄工程调水过程中,水量-水位联动关系十分复杂且非线性,调水过程影响因素众多[1,2,6]。对于高度非线性复杂的调水工程输水系统,优化计算过程需要重复调用耦合模型,计算量大且十分耗时,因此亟需寻求高效的方法以提高工作效率。
近年来基于代理模型(Surrogate Model)的优化策略受到国内外学者的普遍关注,提高了系统的优化效率[7-9]。代理模型是通过数学模型逼近一组输入变量(独立变量)与输出变量(响应变量)的方法,通过寻求输入输出变量间响应关系,可代替真实系统快速给出所求解,目前在流体动力学方面应用十分广泛,已实现机翼、车头、进出水口等的体型优化[9-12]。对于非线性复杂问题,径向基函数(Radial Basis Function,RBF)代理模型具有结构简单、运算稳定、处理高阶非线性数学问题能力强等特点,是较为常用的代理模型[9]。Broad等[13]建立了基于RBF代理模型的水资源配置模型,实现了基于风险的水资源优化配置。显然,该RBF代理模型在调水工程方面具有很好的应用前景。
本文以南四湖下级湖为研究对象,基于RBF代理模型建立调水过程优化模型,以泵站工作总时间最短为目标,考虑水量平衡和水位约束,研究下级湖优化调水过程。将调水过程方案优化结果与耦合模型计算该方案结果进行对比分析,验证求解方法的可行性,在保证计算精度的前提下提高优化效率,得到调水过程最优方案。
2 研究区域与研究思路
2.1 研究区域南四湖是南水北调东线输水干线上的重要调蓄湖泊,湖腰兴建的二级坝枢纽工程将南四湖分为上、下级湖。二级坝闸以下为下级湖,南北长58 km,湖底高程30.80 m,死水位31.30m,正常蓄水位31.80 m,调水时调蓄水位按33.30 m控制。南四湖下级湖包含3个泵站、1个城市用水分水口,其中韩庄泵站与蔺家坝泵站为调入泵站,提水进入下级湖,泵站设计流量分别为125 m3/s 和75 m3/s;二级坝泵站为调出泵站,提水由下级湖进入上级湖,泵站设计流量为125 m3/s;枣庄市薛城区分水口由潘庄引河分水至城区(图1)。

图1 南水北调东线两湖段及南四湖下级湖示意图
根据《山东省水资源综合利用中长期规划》(2016),近期规划年2020水平年95%保证率调水,调入下级湖水量23.59亿m3,调出下级湖水量15.05亿m3,枣庄市薛城区分水2000万m3,调水期为汛期末10 月1日至翌年5月31日,共243 d。根据《南水北调东线第一期工程可行性研究总报告》(2015),二级坝泵站泵前最低运行水位30.58 m,泵站前池进口底高程27.80 m,进水闸底高程27.30 m。
2.2 研究思路本文以南四湖下级湖为研究对象,基于RBF代理模型建立调水过程优化模型,优化下级湖调水过程。首先根据调水过程方案参数区间自动选取80个调水过程方案样本,并利用一维二维耦合水动力模型对每个方案计算,得到不同样本(调水过程方案)的时间-水位关系,选取二级坝泵站为研究关键点,选取最高水位和最低水位为研究关键水位;其次基于RBF代理模型利用样本及耦合模型计算的水位结果,建立并验证调水过程方案与最高水位、最低水位的响应关系;最后基于RBF代理模型建立调水过程优化模型,并采用粒子群算法全局寻优,求解调水过程最优方案。
3 调水过程方案样本选取
根据调水过程方案参数区间自动选取调水过程方案样本,并利用一维二维耦合水动力模型对每个方案计算,得到不同样本的最高水位和最低水位,样本及其水位结果用于RBF代理模型建立与验证。
3.1 一维二维耦合水动力模型在实际工程中,当对河湖系统进行整体水动力模拟时,最直观有效的方法是对湖泊采用平面二维模型、对河流采用一维模型,最终建立一维二维耦合水动力模型[14-16](简称耦合模型)。耦合模型控制方程为连续性方程和动量方程[17-19]。
一维数学模型控制方程:
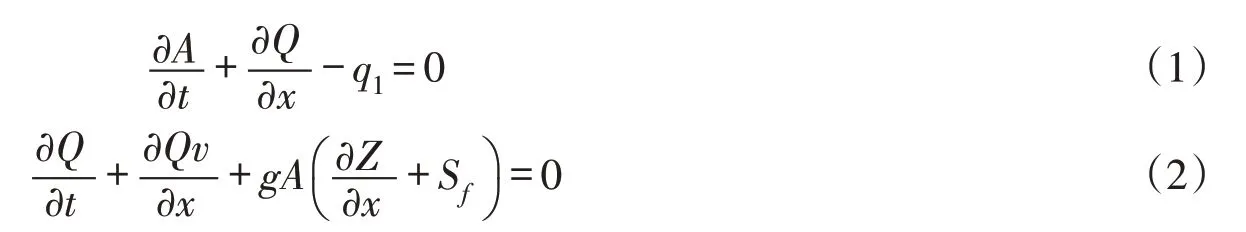
式中:A为过水断面面积,m2;Q为流量,m3/s;x为纵轴坐标,m;t为时间,s;q1为单位长度侧向入流量,m2/s;v为纵向流速,m/s;Z为水位,m;Sf=Q |Q |/K2,K为流量模数,m3/s;g为重力加速度,m/s2。
二维数学模型控制方程:

式中:u、v 为沿x、y 方向的流速,m/s;h 为水深,m;q 为汇/源流量,m3/s;νt=Dhu*,νt为水平涡黏系数,m2/s;D为混合系数,在主航道与深湖区取0.11 ~0.26,浅湖区取0.3 ~0.77,湖周区域取u*为摩阻流速,m/s;R 为水力半径,m;J 为水力坡度;cf为河床摩擦系数,s-1; |V |为u和v的合流速,m/s;C为谢才系数;f为科氏系数,s-1。
对南四湖下级湖建立耦合模型,模型的求解方法、参数率定以及验证详见文献[2]。在计算时,利用耦合模型,输入初始与边界条件,实现南四湖下级湖水动力计算,求得下级湖时间-水位关系。在调水工程中,起调水位、泵站调水流量、泵站开启时间差都影响着水位变化[1-2,20-21]。因此,选用起调水位、泵站开启时间差、调入时间、调出时间四个参数变量表征调水过程方案,选用二级坝泵站处最高水位、最低水位为调水过程结果,用于调水过程优化研究。
针对耦合模型,给出初始条件起调水位、边界条件调入调出泵站工作的时间-流量关系以及一维河道下游水位过程关系,求解得到研究区域内任一点水位过程。例如,起调水位为31.66 m,调入泵站韩庄、蔺家坝泵站从调水第一天起分别以100.97 m3/s和60.58 m3/s流量工作169 d,调出泵站二级坝泵站从调水第20 天起以125 m3/s 流量工作140 d,潘庄引河等在研究时间域内以定流量不间断分水,引河下游为流量水位条件,通过求解耦合模型得到研究区域内任意一点水位变化,提取二级坝泵站处水位结果,得到最高水位33.22 m和最低水位30.94 m。
3.2 调水过程方案样本选取采用最优拉丁超立方设计(Optimal Latin hypercube design,Opt LHD)在调水过程方案参数区间内自动选样,调水过程方案由起调水位、泵站开启时间差、调入时间、调出时间四个参数构成,列于表1。下级湖调水期为非汛期共243 d,假定调入泵站从调水期第一天开始调水且两泵站同时启闭,泵站开启时间差为调入泵站与调出泵站开启时间间隔,且泵站开启时间差与调出时间之和不大于243 d。构建RBF 代理模型至少需要2a+1个建立样本,a 为输入变量个数,参考姚拴宝等[10]、邱亚松等[22]研究中样本数量的选取,考虑提高代理模型精度及减少耦合模型计算时间,本文选取60个建立样本,并额外选取20个验证样本,每个样本代表一种调水过程方案,基于选好的样本采用耦合模型计算得到二级坝泵站处最高、最低水位。

表1 调水过程方案参数区间
4 基于RBF代理模型的调水过程优化模型
根据样本及其水位结果建立并验证RBF代理模型,形成调水过程方案与最高水位、最低水位的响应关系;基于RBF代理模型建立调水过程方案优化模型,并采用粒子群算法全局寻优,得到调水过程最优方案。
4.1 RBF代理模型RBF代理模型是一种多变量空间差值方法,可以表示为径向对称基函数的线性加权和形式[9]:

式中: x 为输入变量,即样本点(调水过程方案);W 为输出变量,即水位结果;w 为权重系数矢量;ϕ( r )为径向函数;r 为待测点x 与第i 个样本点xi之间的欧氏距离,径向函数选用高斯函数,式中c 为形状系数,影响着代理模型的近似精度,c 的最佳取值由样本数量和散布特性确定[9,23],本文参考相关研究c=1.133。
采用RBF代理模型建立调水过程方案与最高、最低水位之间的响应关系。利用60个建立样本及其最高、最低水位,建立RBF代理模型;利用20个验证样本对RBF代理模型进行精度评估。本文选用的精度检验指标有以下几种参数:复相关系数R2、平均相对误差Ravg、最大相对误差Rmax、均方根误差RMSE。
RBF代理模型验证样本的近似值结果与耦合模型的模拟值结果相关性分析如图2和图3所示,最高水位近似值与模拟值的R2为0.9591,最低水位近似值与模拟值的R2为0.9690,近似值与模拟值相关性较好。采用水深值对验证样本的结果进行相对误差分析,水深的Ravg不超过0.0298,Rmax不超过0.0693,RMSE 不超过0.1290。RBF 代理模型精度参数列于表2,其计算结果与模拟值相比,相关性较高,相对水深误差较小,为避免重复调用耦合模型,可采用代理模型方法计算调水过程水位结果。

图2 最高水位近似值与模拟值相关性分析

图3 最低水位近似值与模拟值相关性分析
4.2 基于RBF代理模型的调水过程优化模型本文研究南四湖下级湖调水过程最优方案。引入RBF代理模型方法,并与优化算法结合,快速求得调水过程最优方案,解决传统方法在人为设定有限个方案内得到较优方案的局限性。
鉴于泵站运行需消耗大量能源,本文以泵站工作总时间最短为目标函数,同时考虑水量平衡、安全水位、研究时间域约束,基于RBF代理模型构建调水过程优化模型。
目标函数:
泵站工作总时间最短,即:

表2 RBF代理模型精度参数

约束条件:
水量平衡约束,湖泊在每一时刻均应满足水量平衡约束,即:

水位约束,最高水位低于南四湖下级湖调水期最高蓄水位,最低水位高于泵站最低运行水位约束,即:

泵站工作时间约束,泵站开启时间差与调出泵站工作时间不超过研究时间域,即:

式中:T入为调入泵站工作时间,T出为调出泵站工作时间,ΔT 为调出泵站与调入泵站开启时间差,d;Q入为入南四湖下级湖水量,Q出为出下级湖入上级湖水量,Q分包括枣庄市薛城区及江苏省部分分水,Q损包括调水期内蒸发渗漏等损失水量,m3;W()t为t时刻二级坝泵站泵前水位。
4.3 粒子群优化算法优化模型的求解采用粒子群优化算法(Particle Swarm Optimization,PSO)。粒子群优化算法来源于模拟鸟类觅食行为的规律性,采用粒子在解空间中追随最优粒子进行搜索[3,24]。空间中每个粒子都有自己的位置,第i 个粒子位置表示为飞行的速度表示为在粒子群每一次迭代中,粒子需要找到两个极值[3]:
(1)个体极值pbest,即粒子本身所找到的最优解,位置为
在找到这两个极值后,粒子的第d维(1 ≤d ≤D)速度vid和位置xid根据如下方程进行更新:

式中:ω 为惯性权重,c1和c2为加速常数,(rand)和(Rand)为两个在[0,1]范围里变化的随机值。
采用粒子群优化算法求解优化模型,算法参数设置见表3。最大迭代次数数值越大,越能保证解的收敛性但影响运算速度;粒子个数一般取20~40,对于比较难的问题可以取100~200;惯性权重系数建议取值0.4~1.4,该值越大越有利于进行大范围的全局搜索,越小越有利于进行小范围的局部搜索,加速常数一般为2[25-26]。结合赖宇阳[25]、安伟刚等[26]优化求解问题参数设置,本文最大迭代次数为100,粒子个数为100,惯性权重采用0.9,加速常数c1和c2均为2,优化完成共搜索104个方案。

表3 优化算法参数设置
5 优化结果分析
采用耦合模型计算调水过程方案时,需通过人为改变边界条件在有限个调水过程方案中得到较优方案。本文基于RBF 代理模型构建了调水过程优化模型,采用粒子群优化算法不断搜索解空间,求解调水过程最优方案;为提高计算效率,引入RBF代理模型方法,基于调水过程方案及其水位结果构建调水过程方案与最高、最低水位响应关系,快速计算得出调水过程方案的水位近似值,避免重复调用耦合模型,提高优化效率。
基于RBF代理模型的调水过程最优方案为起调水位31.60 m,泵站开启时间差10.81 d,调入时间149.92 d,调出时间140 d,此时最高水位为33.30 m,最低水位为30.58 m。将最优方案参数输入到耦合模型并计算,基于RBF代理模型的调水过程最优方案结果与耦合模型计算该方案的结果对比列于表4。采用水深值对结果进行比较分析,其绝对水深误差不超过0.05 m,相对水深误差不超过0.99%,结果十分相近。基于RBF代理模型的调水过程优化模型精度高,且求得调水过程方案参数范围内的最优方案。

表4 调水过程最优方案结果与耦合模型计算结果对比
根据《南水北调东线第一期工程可行性研究总报告》(2015),南水北调东线全线汛期243 d调水,即当起调水位为31.8 m时开始调水,调入调出泵站同时开始工作且工作时间为243 d,将此方案作为优化计算的初始方案。基于RBF代理模型的调水过程最优方案与初始方案参数均列于表5,最优方案泵站工作总时间289.92 d,与初始方案相比总工作时间大大减少。
基于RBF代理模型的调水过程最优方案与初始方案的时间-水位关系见图4,初始方案最低水位30.32 m,最高水位33.20 m,最低水位低于泵站安全运行水位(30.58 m),调水时会危及泵站运行安全。基于RBF 代理模型的调水过程最优方案最低水位30.58 m,出现在10 月18 日,最高水位33.25 m,出现在3 月1 日。相比初始方案,最优方案的水位更符合要求,最高水位更接近防洪限制水位(33.30 m),且出现于调水中期,而后水位下降为汛期准备。以正常控制水位32.80 m 为界,最优方案从1月16日到输水结束共136 d,远多于初始方案从3 月20 日到输水结束的73 d,因此最优方案更充分利用了湖泊的调蓄能力。
在调水过程方案参数中,起调水位为南四湖下级湖汛末水位,在调水时起调水位已知。考虑实际调水情况,采用基于RBF 代理模型的调水过程优化模型计算不同起调水位时的调水过程最优方案。选取低于死水位0.10 m,高于正常蓄水位0.10 m,步长间隔为0.10 m的不同起调水位,计算得到不同起调水位下的调水过程最优方案,列于表6。当起调水位为31.60 m 时,此时泵站开启时间差、调入时间天数均最小,分别为10.73 d和149.93 d。当起调水位大于31.60 m时,泵站开启时间差、调入时间天数均有所增加,当起调水位小于31.60 m时,二者天数也会有所增加。同时,当起调水位为31.60 m 的最优方案与前文的调水过程最优方案十分接近,由此可见,当起调水位为31.60 m 时,此时最适合开始进行调度,且此时的调水过程最优方案的泵站工作总时间最短。

图4 调水过程最优方案和初始方案时间-水位关系图
6 结论
采用耦合模型计算调水过程方案时,需通过人为改变边界条件在有限个调水过程方案中得到较优方案。鉴于当前调水过程方案主要依靠主观因素且不易获得最优方案的问题。本文以泵站工作总时间最短为目标,考虑水量平衡和水位约束,基于RBF代理模型构建调水过程优化模型,以南水北调东线山东段南四湖下级湖为研究对象,研究下级湖调水过程最优方案。
(1)本文提出的基于RBF代理模型的调水过程优化模型,首先根据调水过程方案参数区间自动选取多个调水过程方案样本,并利用耦合模型对每个方案计算其水位结果;其次采用RBF代理模型建立并验证调水过程方案与最高水位、最低水位的响应关系;最后采用粒子群优化算法求解基于RBF代理模型的优化模型,得到调水过程最优方案。该方法解决了传统优化方法的局限性,易于得到最优解。
(2)利用所提出的方法研究了南四湖下级湖调水过程,其调水过程最优方案为起调水位31.60 m,调入时间149.92 d,调出时间140 d,泵站开启时间差10.81 d。基于RBF代理模型的调水过程最优方案结果与耦合模型计算该方案结果的绝对水深误差不超过0.05 m,相对水深误差不超过0.99%,结果一致,模型精度高。
(3)基于RBF代理模型的求解的南四湖下级湖调水过程最优方案与初始方案相比,泵站工作总时间由486 d缩短至289.92 d,且更充分利用了湖泊的调蓄能力。考虑实际调水情况,采用基于RBF代理模型的调水过程优化模型,求得不同起调水位下的调水过程最优方案,为实际工程调水提供参考。
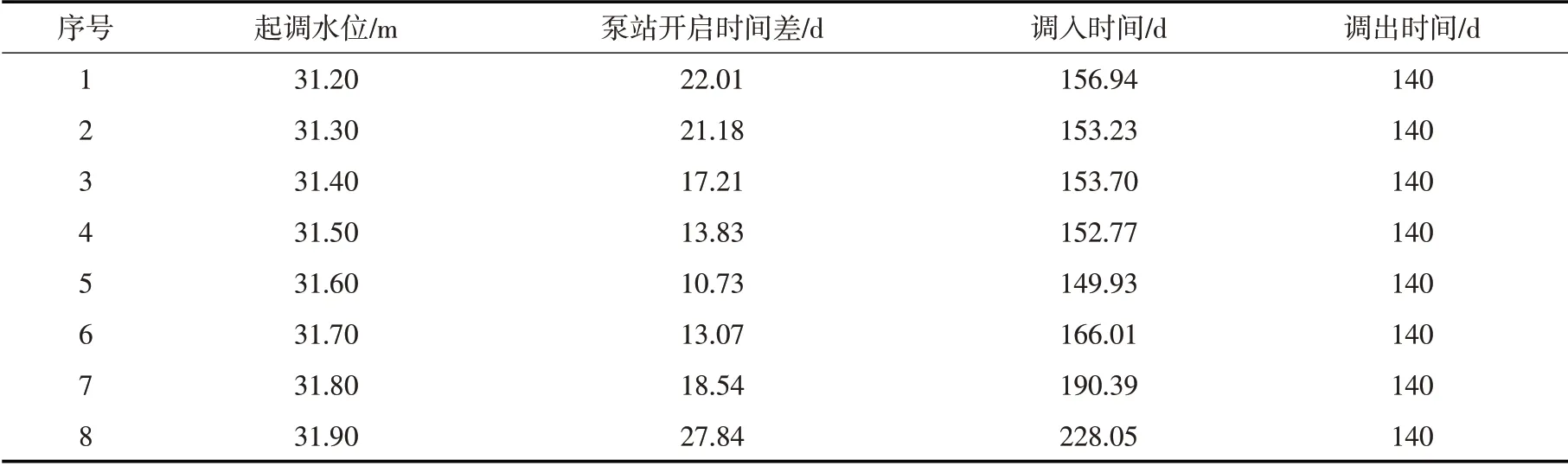
表6 不同起调水位时的调水过程最优方案

