GFRP增强混凝土圆柱轴压强度尺寸效应:细观分析
金 浏,李秀荣,杜修力,樊玲玲
(北京工业大学 城市减灾与防灾防护教育部重点实验室,北京 100124)
1 研究背景
纤维增强复合材料(Fiber Reinforced Polymer/Plastic,FRP)是由纤维材料与基体材料(树脂)按一定的比例混合后形成的高性能型材料,主要包括碳纤维(CFRP)、玻璃纤维(GFRP)、芳纶纤维(AFRP)及硼纤维(BFRP)等。GFRP 由于其成本低廉而广泛应用于混凝土结构构件的加固中,如外贴GFRP 混凝土梁及GFRP 约束混凝土柱等。其中,GFRP 约束混凝土柱的破坏机理及尺寸效应引起了国内外研究者的广泛关注,如Thériault等[1]对GFRP 材料加固混凝土圆柱体试件(最大截面直径为304 mm)的尺寸效应和长细比问题进行了研究,表明对于圆柱半径小于25 mm 的小尺寸混凝土柱,GFRP 约束对尺寸效应影响较小。Berthet等[2]对圆形截面混凝土短柱缠绕GFRP 进行了轴压试验,发现缠绕GFRP 布可以提高圆形截面混凝土短柱的延性。Sheikh等[3]对GFRP 布加固钢筋混凝土柱的抗震性能进行了试验研究,表明GFRP的约束效果好,加固后柱子的承载力、延性以及耗能能力均显著提高。Manuel 等[4]研究了尺寸效应和相对刚度对GFRP 混凝土圆柱(最大截面直径为250 mm)轴压性能的影响,发现采用相同层数的GFRP 布约束横截面尺寸相同的混凝土柱,不同高度试件之间的尺寸效应不明显,但在GFRP 布层数相同条件下圆柱直径从150 mm 增加到250 mm 时,轴压强度逐渐降低,存在部分尺寸效应。Benzaid等[5]开展了FRP约束混凝土方柱的试验,认为外包GFRP能显著提高试件在轴压荷载下的强度且GFRP层数和拐角半径是影响试件性能的主要参数。于洋等[6]试验和模拟研究了轴压作用下GFRP约束钢筋混凝土柱(最大截面直径为350 mm)的破坏行为,分析了GFRP约束混凝土柱的尺寸效应与规律,试验结果表明,GFRP钢筋混凝土圆柱轴压破坏存在尺寸效应,且随着体积配置率增大,尺寸效应明显削弱。詹界东等[7]试验研究了混凝土强度等级对GFRP布约束混凝土圆柱(最大截面直径为250 mm)尺寸效应的影响,发现混凝土强度越高,GFRP 约束钢筋混凝土柱的抗压强度越高,且试件尺寸越大,极限抗压强度的提高程度越大,但混凝土强度较高时,极限抗压强度提高幅度减小,试件延性变差,更容易发生脆性破坏。
这些研究工作促进了对GFRP约束混凝土柱力学行为的认识。尽管如此,这些研究仍存在以下不足:(1)所研究的试件尺寸偏小,最大截面直径约为350 mm;(2)对GFRP 约束混凝土柱破坏机理的认识还远远不足;(3)尚未厘清GFRP约束作用对混凝土柱轴压破坏尺寸效应的影响机制与规律,更无相关的尺寸效应律可供借鉴。因此,研究大尺寸GFRP约束混凝土构件的破坏机制及其尺寸效应,完善和发展相关的理论分析模型,修正现行基于小尺寸试验研究结果的GFRP混凝土结构设计理论与方法,不仅具有重要的科学意义,并且对于大尺寸GFRP约束混凝土结构的科学与合理设计具有重要的工程指导意义。
为深入研究GFRP约束混凝土柱轴压破坏行为及其尺寸效应规律,本文以圆柱为研究对象,从细观角度出发,考虑到混凝土非均质性及GFRP与混凝土间复杂的相互作用,建立GFRP约束混凝土柱的细观力学分析模型,讨论GFRP约束作用对柱破坏机理及尺寸效应的影响规律与机制。最后,结合GFRP影响机制,在混凝土材料尺寸效应律的基础上,建立GFRP约束混凝土圆柱轴压破坏行为下的尺寸效应半经验-半理论公式。
2 3D细观模型建立
实际上,GFRP约束混凝土柱轴压破坏尺寸效应主要取决于两方面的原因:(1)混凝土及GFRP材料本身的非均质性和易脆性;(2)GFRP 与混凝土柱间复杂的非线性相互作用[8]。因此,合理的数值分析模型应能反映该两方面的全部“特征”。宏观尺度数值模型(即混凝土看作为均匀各向同性材料)不能反映混凝土的非均质性,故而其不能够描述材料层次的尺寸效应,因此数值模型中需材料细/微观尺度模型来描述。
2.1 GFRP约束混凝土圆柱相互作用细观模型建立为反映混凝土内部组成的非均质性,本文从细观角度出发,将混凝土看成骨料、砂浆及界面过渡区组成的三相复合材料[9-11]。依据各细观组分的几何特征,运用Monte-Carlo 方法,借助于Fortran 编程将骨料颗粒(假定为球体,最小等效粒径为16 mm,最大等效粒径为30 mm,体积分数约为30%)随机投放到砂浆中,考虑到计算效率的限制,界面过渡区厚度设置为1 mm[12],网格平均划分尺寸为5 mm。圆柱底部约束采用固定约束,上部为自由约束,采用单调位移加载的方式进行加载,建立了GFRP约束混凝土圆柱3D细观模型,如图1所示。

图1 GFRP约束混凝土圆柱3D细观数值模型
2.2 本构关系模型混凝土类水泥基材料在外荷载作用下,除了会由于损伤而导致材料产生刚度退化现象的产生,还会出现不可恢复的塑性永久变形。近年来,研究者结合弹塑性和损伤力学两种理论框架来描述混凝土的力学行为,如Grassl等[13]、Badel等[14]及Kim等[15]的研究工作。由Lubliner等[16]提出,并经由Lee等[17]改进的塑性损伤模型,不仅能够表征混凝土在外荷载作用下的塑性永久变形,而且能够描述混凝土由于损伤累积而导致的刚度退化及达到强度后的材料软化力学行为。该混凝土材料本构模型可以描述单调加载、周期性往复加载、低围压及动力加载问题等,因此得到众多学者广泛的应用。
本文参考文献[11-12],对砂浆基质和界面过渡区采用上述塑性损伤模型来描述其力学行为。骨料颗粒强度较高而不破坏,因此将其设定为弹性体。相关试验[18]表明:FRP材料的应力-应变关系接近于理想弹性,因此可设定GFRP为理想弹性材料。为避免或削弱由于应变软化而导致计算中出现的网格敏感性问题,塑性损伤本构模型中上升段曲线采用应力-应变关系曲线,而下降段曲线则采用应力-位移关系来替代应力-应变关系曲线,即通过设定断裂能唯一的方法来缓解网格敏感性问题。
需要说明的是,混凝土细观组分采用八节点六面体实体单元来进行离散;GFRP采用壳单元进行离散,其破坏准则为最大拉伸应变准则,即纤维达到其有效断裂应变时产生破坏停止计算。
2.3 数值分析方法的验证为了与试验结果对比,有限元分析中的GFRP 和混凝土圆柱的参数采用文献[19]中的5个GFRP 约束混凝土轴心受压圆柱试件的数据,试件的尺寸为ϕ150 mm×450 mm,混凝土立方体抗压强度为39.67 MPa,约束所用的GFRP 为玻璃纤维布,纤维布的计算厚度为0.169 mm,极限应变为3.2%,实测抗拉强度为3271 MPa,弹性模量为87 GPa。GFRP布加固的范围为柱的整个侧面,其中C0 试件为对比试件,未贴GFRP 布,C1、C2、C3、C4 试件分别外包1、2、3、4 层GFRP 布。本文引进体积配置率作为约束参数,即C1、C2、C3、C4 的体积配置率分别为0.45%、0.9%、1.35%、1.8%。其中体积配置率ρf[6]:

式中:ρf为GFRP体积配置率;n为外包GFRP层数;t为GFRP单层厚度;D为柱横截面直径。
文献[19]的物理试验中并未单独测量界面过渡区的力学参数(如弹性模量、泊松比及强度等),且目前在国际上尚缺乏能得到广泛认可的测量界面过渡区力学参数的方法。针对于此,研究者采取的一致做法是反复试算法,包括文献[11-12]。本文依然采用反复试算的方法确定界面相的材料力学性质(尤其是强度参数)[20],具体做法是:对界面区取砂浆力学参数折减数值,对边长为150 mm的混凝土立方块单轴压缩/单轴拉伸破坏过程进行大量的数值试验,发现采用表1中给出的界面相及砂浆基质力学参数,包括抗压强度、抗拉强度及弹性模量等参数时,模拟得到的混凝土单轴抗压强度是39.6 MPa,与试验实测结果38.6 MPa基本吻合,说明了参数选取的合理性。

表1 混凝土细观组分及GFRP力学参数
基于本文数值方法模拟得到了尺寸为ϕ150 mm×450 mm不同体积配置率下的GFRP约束混凝土圆柱破坏过程。以体积配置率为0.9%的C2 试件为例,如图2 所示(损伤因子ω=0 表示混凝土柱完好无损,ω=1表示混凝土柱完全破坏;u为压缩后的轴向位移)。因GFRP为线弹性材料,在加载过程中,随着荷载的不断增大,混凝土柱内部裂缝不断扩展,直至某一时刻发展到混凝土柱表面,表面裂缝处纤维内力瞬间增大。由于GFRP布并不具备内力重分布的能力,因此导致裂缝处纤维丝先行发生断裂,单丝断裂后能量的释放将影响到周围的纤维丝,致使周围应力较大的纤维丝相继发生断裂,此时并未达到GFRP 布的极限拉应变,故认为弹性应变达到其有效断裂应变时柱子失效破坏,计算停止。根据文献[21]中的建议,取GFRP的有效应变系数为65%(EE为GFRP弹性应变,当弹性应变达到极限应变的65%时,即EE达到0.02时,认为GFRP达到有效断裂应变表现为拉断破坏)。图2为核心混凝土内部损伤过程和不同阶段GFRP的应力和弹性应变分布云图(S为最大主应力),从图2可以看出,核心混凝土在中心区域最先产生微裂缝,接着裂缝向周围发展,在柱中上部区域形成环向的主裂缝,主裂缝的形成使混凝土发生随轴向压力增大而增大的横向膨胀变形,从而使GFRP产生很大的拉应变,直至达到有效断裂应变,GFRP 部分断裂,失去对核心混凝土的约束作用导致柱失效破坏,这与试验结果的破坏形态是一致的。

图2 GFRP与核心混凝土的破坏过程

图3 素混凝土柱与GFRP约束下核心混凝土破坏形态对比
图3为模拟得到的尺寸为ϕ150 mm×450 mm 的素混凝土圆柱与在体积配置率ρf=0.9%的GFRP 约束下核心混凝土的破坏形态对比图。从图3可以发现,素混凝土柱破坏形态呈典型的压-剪破坏模式,而包裹GFRP 的核心混凝土为压碎破坏形态,这是因为GFRP的横向约束作用限制了核心混凝土主裂缝的斜向发展,从而使核心混凝土的破坏比较均匀。
图4 是本文数值模拟得到的试件的轴向名义应力-名义应变曲线(名义应力为轴向荷载与横截面面积的比值,名义应变为加载端产生的竖向位移与试件高度的比值)与试验应力-应变曲线的对比,从图4可以发现两者吻合良好。综上所述,试件的模拟结果与试验结果有较好的一致性,说明了本文数值方法的准确性与可行性。
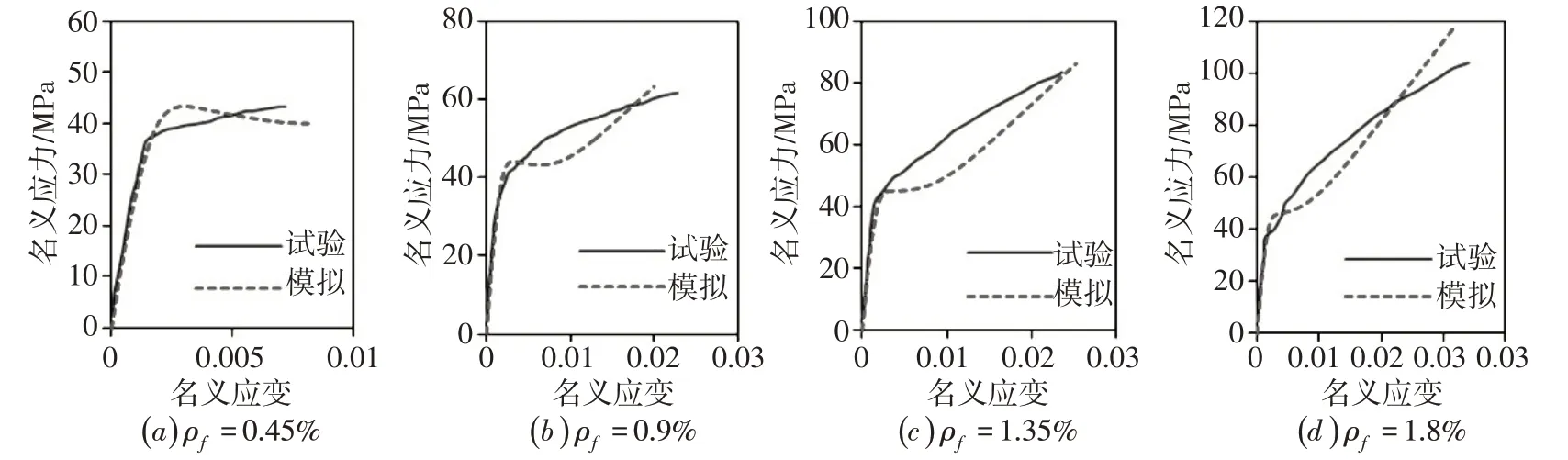
图4 试验与模拟结果名义应力-名义应变关系对比
3 体积配置率对柱尺寸效应的影响
3.1 模拟结果为揭示横向约束作用对核心混凝土轴压破坏行为及其尺寸效应的影响,在上文已验证的细观力学数值分析模型与方法的基础上,开展不同横向约束作用(以体积配置率表征)及更大尺寸的GFRP约束混凝土柱轴压下的细观数值模拟分析。
表2 给出了试件的设计参数。采用几何相似比关系(1∶2∶4)设计了不同截面尺寸(ϕ200 mm×600 mm、ϕ400 mm×1200 mm、ϕ800 mm×2400 mm)及5 种体积配置率(CA 系列:ρf=0%,CB 系列:ρf=1.352%,CC 系列:ρf=2.704%,CD 系列:ρf=5.07%,CE 系列:ρf=10.14%)的GFRP 约束混凝土圆柱,其中表中“S”、“M”、“L”分别代表小、中、大3种尺寸。

图5 不同尺寸下GFRP约束混凝土柱的名义应力-名义应变关系曲线
3.2 尺寸效应分析图6是CB系列即在GFRP 体积配置率为1.352%的情况下,3种不同尺寸柱的最终破坏模式。从图6可以看出,在约束作用相同、几何尺寸相似的情况下,两个较小尺寸柱的破坏模式差异不大,典型的压-剪破坏模式基本消失,均是在柱中部区域发生混凝土压碎破坏,而大尺寸的混凝土柱还呈现压-剪破坏形态,在柱中部区域产生多条斜裂缝。说明约束作用相同且体积配置率较小的情况下,相比于大尺寸混凝土柱,GFRP对小尺寸混凝土柱的约束效果更好,使其破坏形态更加均匀。
图7是3种尺寸在5种配置率下的轴向名义应力-名义应变关系曲线。由图7可见,不同尺寸试件的应力-应变曲线有着明显差异。在同一体积配置率ρf下,GFRP混凝土柱的名义应力随尺寸增大而减小,且随着体积配置率的增大降低幅度减小,存在明显的尺寸效应。当柱子为素混凝土柱时,几何相似的柱子尺寸越小峰值应力和极限应力越大,尺寸效应最为显著。随着GFRP体积配置率增大,
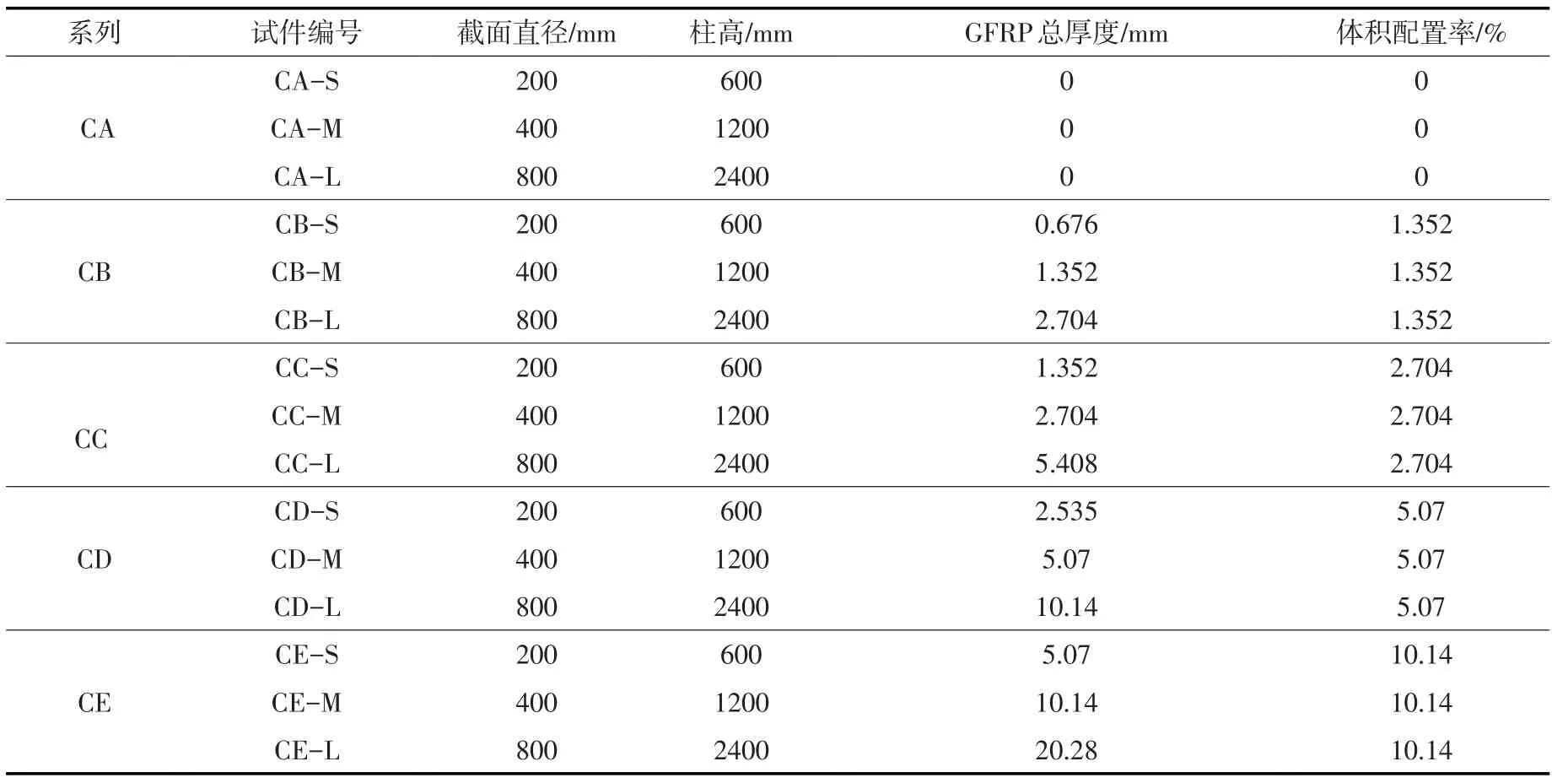
表2 试件设计参数
图5 为试件截面直径分别为200、400、800 mm 的GFRP 约束混凝土圆柱在不同体积配置率下的轴向名义应力-名义应变关系曲线,从图5 可以看出,3 种尺寸的名义应力-应变曲线均呈现3 种形式:(1)GFRP体积配置率较小时,约束作用较弱,应力-应变曲线达到峰值点后迅速下降,且不再回升(对应于曲线①);(2)随体积配置率增大,曲线达到峰值应力后下降,继而由于GFRP的较强约束而逐渐回升(对应于曲线②);(3)当体积配置率继续增大,约束作用为强约束时,曲线不再出现下降段,而是呈双线性持续上升(对应于曲线③)。
从图5 还可以看出,试件尺寸对应力-应变曲线类型基本没有影响。相比于素混凝土柱,GFRP约束混凝土柱的极限抗压强度(数值上为极限压缩荷载所对应的名义应力值)和其对应的极限应变都有显著提高。另外,随着体积配置率增大,极限抗压强度提高幅度更大,极限应变也更大。实际上,这是因为由于GFRP的存在,使核心混凝土处于三向受压应力状态,围压作用将限制混凝土内部裂缝数量以及裂缝宽度的发展,最终使GFRP混凝土柱的强度得到提高,且延性能力亦得以增强。不同尺寸试件的名义应力-名义应变曲线差异不断减小。当GFRP体积配置率达到10%左右时,不同尺寸试件的应力应变曲线几乎完全重合,尺寸效应现象消失。该模拟结果与陈思同[22]和于洋等[6]的试验结果吻合。这是因为随着体积配置率的增大,GFRP对核心混凝土的约束增强,限制了其内部裂缝的发展,不仅提高了混凝土的强度和变形能力,而且削弱了尺寸效应的影响。
图8 给出的是在不同体积配置率下,15 根约束混凝土柱名义轴压强度与截面直径的关系。这里,对于素混凝土柱,名义轴压强度为轴向荷载达到峰值荷载时的名义应力值;对于GFRP约束混凝土柱,名义轴压强度为构件失效破坏(即GFRP的弹性应变达到其有效断裂应变)时,轴向荷载达到极限荷载时的名义应力值。名义轴压强度定义为:

式中:Pu、σNu、D分别是极限荷载、名义轴压强度和截面直径。名义轴压强度σNu为轴向荷载达到极限荷载Pu时的名义应力值。
从图8中可以看出,约束混凝土柱的名义轴压强度随着截面尺寸的增大而减小,即存在尺寸效应现象。素混凝土柱名义轴压强度随尺寸增大降低明显,尺寸效应显著。随着GFRP体积配置率增大,相同尺寸的GFRP混凝土柱名义轴压强度增强。GFRP体积配置率相同时,柱子名义轴压强度的提高幅度随尺寸增大而增大。另外,还可以发现:当体积配置率达到10%左右时,3种尺寸试件名义轴压强度基本无差异,即尺寸效应几乎完全消失。
目前,Bažant基于断裂力学理论建立的断裂力学尺寸效应理论[23]能够对混凝土材料失效行为进行数学及物理机制的描述,较好地反映混凝土材料破坏尺寸效应行为,因此被越来越多的学者所接受和使用,该尺寸效应律的表达式为:

图7 不同配置率下GFRP约束混凝土柱的名义应力-名义应变曲线

图9 素混凝土柱数值结果回归分析

图8 名义轴压强度与截面直径关系

式中:σNu为名义强度;fc为混凝土材料抗压强度(这里取最小尺寸素混凝土柱的抗压强度模拟值);B、D0为依赖于结构的几何常数;D为试件尺寸,本文为柱的直径。
将式(3)转化成线性形式:

本文fc采用尺寸ϕ200 mm×600 mm 素混凝土柱的抗压强度模拟值,即为33.31 MPa。通过线性拟合分析,可以得到B=1.542,D0=132。
对素混凝土柱模拟结果(强度参数)进行回归分析,在确定尺寸效应参数的基础上,可以获得名义强度随尺寸变化的双对数曲线,如图9所示。图9为模拟得到的素混凝土柱名义强度数据点(两组数据点,即模拟1 和模拟2 表示两组强度,通过两组不同骨料分布的数值构件来计算获得)与Bažant尺寸效应律(SEL)、线弹性断裂力学理论(LEFM,针对完全脆性材料,斜率为-1/2)以及塑性强度理论(Strength criterion,针对塑性材料,不具有尺寸效应)的对比情况,可看出拟合良好(R2=0.98),说明Bažant尺寸效应律能够较好的描述素混凝土柱轴压强度的尺寸效应规律。
4 GFRP约束混凝土圆柱尺寸效应理论
4.1 轴压强度半经验-半理论公式的提出实际上,GFRP约束混凝土圆柱(含纵筋)在轴压加载下的承载力可表示为:

含纵筋的GFRP约束混凝土圆柱的总承载力由GFRP约束混凝土圆柱的承载力Nu和纵筋的承载力NS共同承担,其中Nu与GFRP混凝土圆柱的尺寸、GFRP缠绕层数等因素有关,NS与纵筋的配置率有关而与试件尺寸无关。

式中:σNu为GFRP约束混凝土圆柱(无纵筋)的名义强度;Ac为GFRP约束混凝土柱的横截面面积。
结合上述分析,可知GFRP 约束作用对混凝土柱轴压破坏行为产生如下影响:(1)强度提高。GFRP为核心混凝土柱提供的侧向约束作用使得混凝土处于三轴受压应力状态,故而提高柱子的轴压强度;(2)尺寸效应削弱。GFRP约束作用将抑制核心混凝土内部变形及裂缝扩展,使得柱的轴压破坏表现出延性特征,故而将削弱强度的尺寸效应。
根据该两方面的影响机制,结合经典的Bažant材料层面尺寸效应律,得知GFRP约束混凝土柱的名义强度σNu可表示为:

式中:φ为强度提高系数,表征GFRP 存在对名义强度的影响;β 为尺寸效应削弱系数,反映GFRP存在对尺寸效应的影响。
4.2 半经验-半理论公式参数的确定
4.2.1 强度提高系数φ 的确定 自从1906年Considere[24]认为作用在混凝土周围的侧向应力对其强度和变形都存在有益影响以来,之后Fardis等[25]、Ahmad等[26]、吴刚等[27]和Lam等[28]根据试验数据提出了各自的强度简化模型。
Lam 等[28]对国外截至当时几乎所有能够收集到的关于FRP 约束混凝土圆柱体的试验数据进行了比较分析,最后给出的FRP约束混凝土圆柱体的强度计算简化模型得到了广泛认可。根据Lam等[28]的研究,可知强度提高系数φ为:

式中:fcc为GFRP 约束混凝土轴心抗压强度; fc为素混凝土柱抗压强度,取最小尺寸直径为200 mm混凝土柱抗压强度模拟值;fl为侧向约束强度;fFRP为GFRP抗拉强度;t为GFRP总厚度;D为柱横截面直径;EFRP为GFRP的弹性模量;εh为GFRP的环向应变;R为截面半径。
4.2.2 尺寸效应削弱系数β的确定 如前文所述,GFRP体积配置率ρf越大,强度尺寸效应的削弱作用越为显著,本文工况下,当体积配置率为10%时,尺寸效应完全被抑制。图10给出了削弱系数β与体积配置率ρf的关系曲线,下面将对其具体说明。
当ρf=0时(即试件为素混凝土柱),β对柱的轴压破坏尺寸效应没有影响,此时β=1。
当ρf≥ρf0时(本文工况下,极限配置率取为10%),由于GFRP 约束作用很强,柱的轴压破坏呈现塑性或延性特征,此时轴压强度的尺寸效应将被完全抑制。该状态下,柱子名义轴压强度与结构尺寸无关,此时对应的名义轴压强度应为:

联立式(7)、式(8)和式(10),可知尺寸效应被抑制时所对应的尺寸效应削弱系数β为:

当0 <ρf<ρf0时,削弱系数β 的值将介于1和之间。实际上,随着GFRP体积配置率的增大,柱轴压破坏将表现出较弱的脆性特征,故而尺寸效应将逐渐减弱,尺寸效应削弱系数β 不断趋近于


图10 尺寸效应削弱系数β的确定
式中:α为调节系数,反映削弱系数β 随GFRP约束作用对尺寸效应影响的快慢,其可通过试验和模拟结果数据拟合来确定。
4.3 尺寸效应半经验-半理论公式的验证
4.3.1 与数值模拟结果的对比 综合式(7)、式(8)及(12)可知,建立的能反映GFRP约束作用定量影响的混凝土柱轴压强度尺寸效应律存在3个参数需要确定,即B、D0和调节系数α。将尺寸ϕ200 mm×600 mm 素混凝土柱模型作为基准试件(其轴心抗压强度fc=33.31 MPa),并将2.2节中素混凝土柱模拟结果回归分析得到的参数B、D0作为基准参数,即B=1.542,D0=132。关于尺寸效应调节系数α,这里则是通过与模拟结果进行反复试算与对比的方法来确定。
结合上述给定参数,将本文半经验-半理论公式与模拟结果进行对比分析,发现当调节系数α的值在24~28之间时,理论预测值与模拟结果吻合良好。故本文建议α取值为26,即α=26。
在此基础上,为验证本文尺寸效应半经验-半理论公式的准确性,在上述已确定参数的条件下,将理论预测结果与更多参数工况(包括更大结构尺寸、更多体积配置率)下的数值模拟结果进行对比如图11所示。从图11可以看出,本文给出的理论预测曲面可很好的与模拟数据点吻合,证实了所提出的GFRP约束混凝土柱圆轴压强度尺寸效应半经验-半理论公式的准确性。
4.3.2 与已有试验结果对比 为更充分地说明本文所建立的半经验-半理论公式的准确性和合理性,这里选取了Manuel等[4](柱子截面直径为150 mm和250 mm,外包2层GFRP)以及卜方坛[29](柱子截面直径分别为100、150和200 mm,每个试件均分别外包GFRP 厚度为2、3和4 mm)的试验结果作为对比分析。

图11 α=26理论值与模拟结果对比
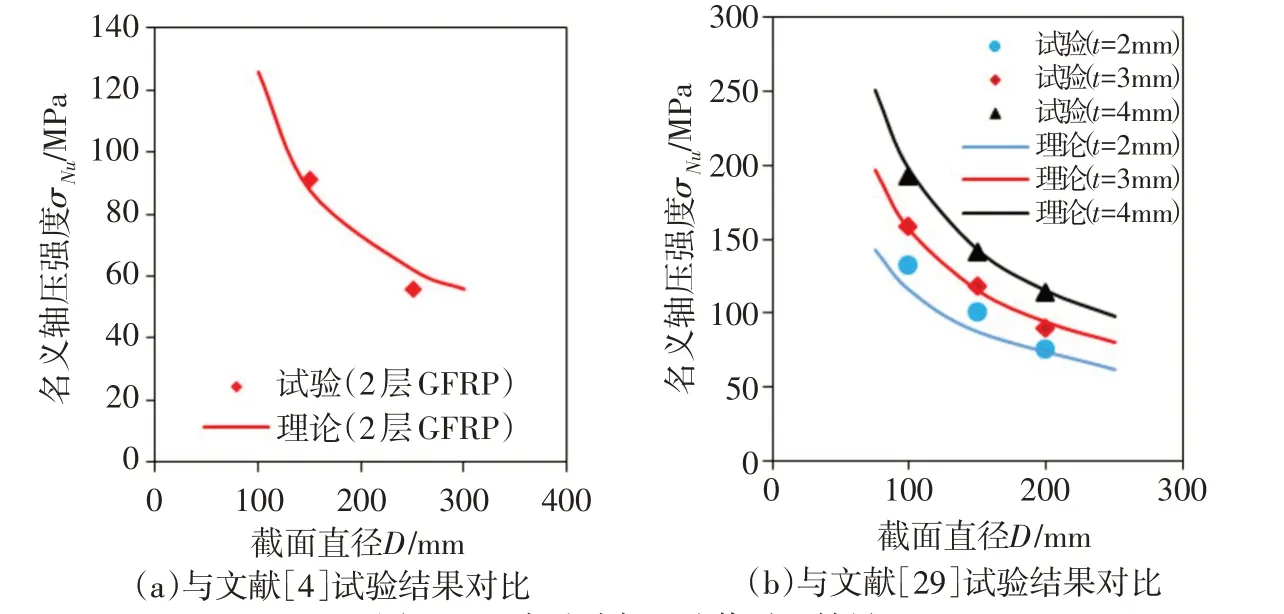
图12 已有试验与理论值对比结果
图12为本文的半经验-半理论公式与已有试验数据[4,29]的对比情况。从图12可以发现,该公式均能与试验结果有较好的吻合。说明本文公式适用于GFRP 约束混凝土柱名义轴压强度的计算是合理的,当然,此公式尚需要大量的试验数据来验证。
5 结论
本文采用细观数值模拟方法研究了结构尺寸及体积配置率对GFRP约束混凝土圆柱轴压破坏机理和失效模式的影响,揭示了横向约束作用对GFRP约束混凝土柱名义轴压强度及其尺寸效应的影响机制与规律,进而建立了能够反映横向约束作用(以体积配置率来表征)定量影响的GFRP约束混凝土柱尺寸效应律。获得的主要结论为:(1)GFRP约束作用使得柱处于三轴受压状态,进而提高柱的轴压承载力及延性能力。(2)本文工况中,不同尺寸GFRP约束混凝土柱破坏模式类似,名义轴压强度具有尺寸效应,GFRP体积配置率较小时,GFRP对大尺寸柱的约束作用弱于小尺寸柱。(3)随着GFRP体积配置率的增大,柱子名义轴压强度的提高幅度随尺寸的增大而增大。(4)随着GFRP体积配置率的增大,轴压强度尺寸效应减弱;本文工况中,当体积配置率约为10%时,名义轴压强度与尺寸近乎无关。(5)建立的构件层次尺寸效应律可有效反映GFRP约束作用对尺寸效应的定量影响,模拟结果和已有试验数据证实了本文半经验-半理论公式的合理性。但需更多试验及理论结果的深入验证。
关于FRP约束混凝土柱的截面形状、加载方式及偏压等对尺寸效应的影响以及对于柱内部含钢筋的名义轴压强度的情况将另文讨论。

