区域范围内工程测量控制网独立坐标系统的选择

王伟彪

（江苏省地质测绘院，江苏 南京 211100）

近年来，随着我国基础建设规模的不断扩大，工程测量控制网独立坐标系统得到了广泛应用[1]。测量控制网由地面上一系列点构成，控制点之间由边长、高差、方向或GNSS基线的测量连接并构成网形，形成点的空间位置，通过已知点的坐标系点之间的连接，按一定方法计算得到[2]。目前，工程测量控制网独立坐标系统，能较好地在区域内实施测量点的控制，满足建设需求，保证工程质量[3]。区域范围内工程测量控制网独立坐标系统的选择，对于区域内工程测量点布局以及下一步的施工定位至关重要，因此，测量人员要结合工程实际，详细计算，得到最优方案[4]。本文以实际工程案例为研究对象，分析了区域范围内工程测量控制网独立坐标系统的优选方法。

1 工程概况

工程坐落在常州市天宁区延陵西路市河以北，主要施工1号风亭、2号风亭和3号出入口。本站为地下二层11m岛式车站，主体结构外包总长度为225.5m（净长223.9m），标准段外包总宽为21.3m（净宽19.7m），埋深为16.31m，总建筑面积为12021.3m2，其中地下面积为11420.5m2，地上面积为600.8m2。本站共设有3个出入口、2组风亭和1个安全出入口。

施工过程中，由于测区距中央子午线的距离和参考椭球面的位置产生的变形各不相同，将产生高斯投影变形改正和高程归化改正，因此，需要修正子午线距离和参考椭球面的位置。修正后的长度与实际长度不一致，要通过建立优选方案，确定区域内工程测量控制网独立坐标系统，减小这两项变形对工程施工测量精度的影响，进一步将综合变形值控制在一个微小的区域范围，满足工程施工放样的精度要求。

2 投影长度变形分析

通常情况下地球表面凸起，曲面不可展平。当高斯正形投影在地球曲面上，边长投影到高斯平面上，长度就会发生变形，导致测量精度失真，施工放样难以达到要求。变形主要是因实测长度投影到参考椭球面上的变形，用ΔS1表示，以及参考椭球面上的边长投影到高斯平面上的变形，用ΔS2表示。

将测量的真实长度归化到统一的参考椭球面上时，应加的改正数（即变形影响值）可由公式（1）计算得到。

公式（1）中，S为实测长度，Hm指平均高程，R指曲率半径。由公式（1）计算得到ΔS1的绝对值，其与Hm的大小成正比。Hm的变化越大，变形影响值也越大。变形值的变化示意图如图1所示。

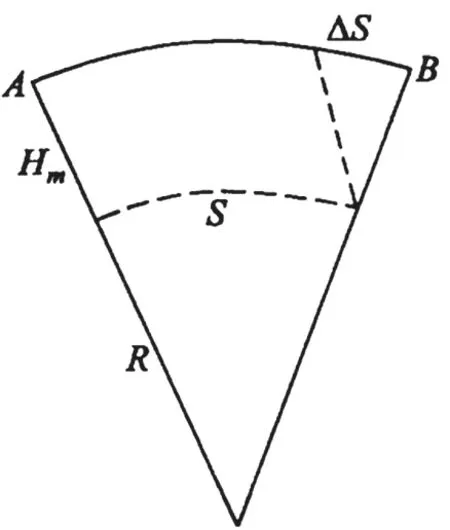
图1 变形值的变化示意图

将参考椭球面上的边长归算到高斯投影面上的变形影响值由公式（2）计算得到。Ym为实测边两端点的横坐标平均值。

3 坐标系统选择

工程设计了三种坐标系统选择方案，三种方案不同抵偿高程面下的中央子午线的高斯投影为3°，以不同控制点桩号为控制网缩放的不动点，测区中心的大地坐标为L=111°10′20″，投影面为1985国家高程基准面的平面直角坐标系统。工程地区已有平面控制网，可沿用原有坐标系统，采用高斯投影3°带，投影面为测区抵偿高程面或平均高程面的平面直角坐标系。

选择一个合适的抵偿高程面，使测区内抵偿投影面上实测长度达到最小，从而得到工程控制网适用的坐标系统。依次将三种方案所测的投影面积与国家标准投影面积对比，最终确定哪一种方案为适用性最佳的坐标系统。具体测量情况如表1、表2、图2与图3所示。

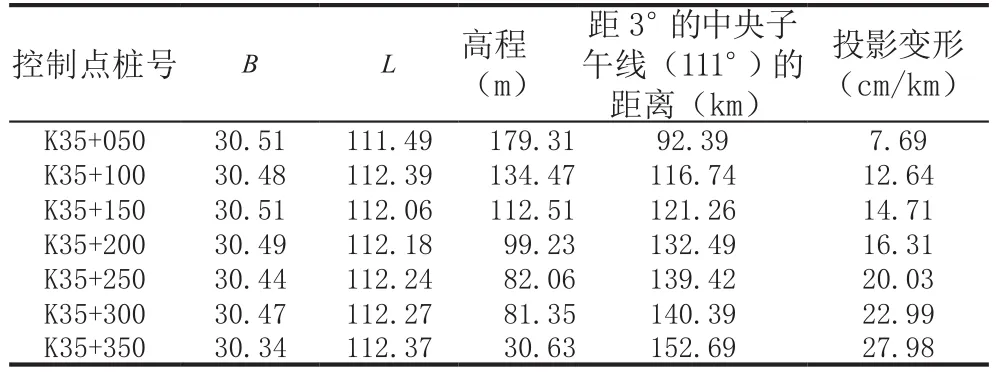
表1 部分控制点点位数据

第一种方案，表1是选择的抵偿改正的7个控制点，分别记录了实测点的高程、B值与L值。这7个控制点具有一定的代表性，能更好地进行底层改正后的全局衡量，得到不同投影变形。（如图2所示）

图2 方案一投影变形情况

根据国家相关规范规定，投影变形不能大于2.5cm/km。图2是不同桩号下的投影变形情况，随着测量距离的增加，投影变形的面积也在不断增加。投影变形的7个点分别为K35+050（7.69cm/km）、K35+100（12.64cm/km）、K35+150（14.71cm/km）、K35+200（16.31cm/km）、K35+250（20.03cm/km）、K35+300（22.99cm/km）、K35+350（27.98cm/km），均大于2.5cm/km，因此，方案一不能作为本工程坐标系统的选择。

表2 方案二与方案三投影情况

图3 方案二与方案三投影情况分布

从表2与图3来看，方案二、方案三与国家标准投影面积对比，均小于2.5cm/km，可实现不同测量方案下长度的综合变形相互抵偿，满足实际精度要求。与方案二相比，方案三的变形值更小，且中央子午线与0°带重合，底层的高层面采用参考椭球面，更符合使用习惯。本次研究由于地处车站区域工程网内，对变形值的要求为毫米级。因此，方案三为最优方案。

4 结论

区域范围内工程测量控制网独立坐标系统的选择，应结合工程实际进行具体测算，需将测量的真实长度归化到统一参考椭球面上，进一步改正数值，即变形影响值，最终确定最优坐标系统，满足施工放样的精度要求，提高施工现场测量水平，保证工程顺利完工。