压气机特性曲线精确分步拟合方法研究

房友龙，刘东风，贺 星，余良武，邓志明

(1.海军工程大学动力工程学院，武汉430033；2.中国人民解放军91663部队，山东青岛266012；3.海军士官学校机电系，安徽蚌埠233012)

1 引言

燃气轮机部件特性是进行热力计算和性能评估的基础，部件特性的精度，特别是压气机特性的精度，对燃气轮机性能计算结果有较大影响。通常，部件特性曲线是在昂贵的装备测试中获得，往往是有限、离散的平面曲线簇的形式，其中的信息不能满足性能计算的需要，还常常需要采用拟合[1-3]、神经网络[4-5]和插值等方法予以进一步处理。神经网络是隐式内部知识表达形式，且往往泛化能力不足。插值法是用网格离散压气机特性图上的等转速线和等效率线，将得到的数据用数据表的形式存储在计算机中进行二维插值求解的方法，其缺陷是当插值点不在网格节点上时计算要经过多次插值才能完成，导致计算量增大、精度降低[6]。拟合有多项式分步拟合[1]和椭圆分步拟合[3]等方法，可以任意精度逼近非线性函数，但拟合阶次过高会产生过拟合现象，以致泛化能力不足。贺星等[6]基于改进Levenberg_Marqardt算法对燃气轮机低压压气机特性进行拟合优化，赵雄飞等[7]提出以残差平方和等5个统计学检验指标来确定燃气轮机部件特性方程的最佳拟合次数，刘喜超[8]提出偏最小二乘方法拟合曲线，涂环[9]提出基于Kriging算法的压气机特性建模，Yang等[10]提出一种利用椭圆坐标缩放、变换和旋转的拟合方法。

文献[1]采用最小二乘法，分两步拟合，两步拟合中间要进行坐标变换，但文中对坐标变换的参数选取方法阐述不够明确，仅说明变换参数取值应使得变换后的各等速线有效流量段相同，对如何保证没有说明。本文在文献[1]、[6]、[7]的基础上，拟改进坐标变换方法，进一步探究拟合中坐标变换的意义，以及第二步系数拟合中牛顿插值法和最小二乘法的适用情形，并用多个指标对拟合结果进行评估，给出拟合阶次的选取方法。

2 特性曲线分步拟合方法

以高压压气机流量拟合为例进行说明。先对压比进行坐标变换，由于不同转速下的变换参数是变化的，故变换参数先对转速进行拟合；在不同转速下，流量对坐标变换后的压比进行多项式拟合；拟合系数再对转速进行多项式拟合。具体如下：

(1)在等折合转速特性曲线右侧划一条曲线作为流量阻塞线，在流量阻塞线和左侧的喘振线间的各等折合转速线上，均取样本点若干。

(2)压比坐标变换。

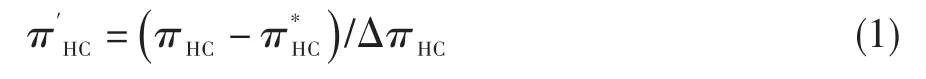
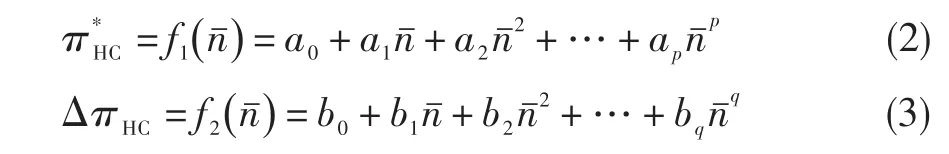
一般情况下，p和q取低阶，不大于3。

(3) 在不同折合转速下，折合流量对π′HC进行r阶多项式拟合。

式中：下标i表示不同的折合转速。

(4)系数Sj,i( j =0,1,…,r)对折合转速进行第二步拟合。

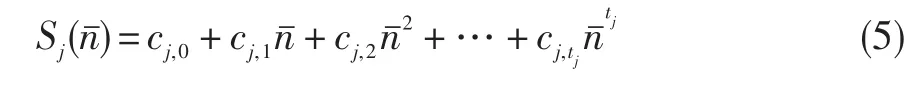
对于等效率线，参考文献[11]的方法，将拟合区域分为两部分：连接每条等效率闭合线的凸点划出一条依据线，将拟合区域分为上半部分和下半部分，分别采用步骤(2)至(4)进行多项式拟合。

关于坐标变换的意义，除文献[1]中所述使变换后的各等速线的压比段大致相同(约为-0.5～0.5，文献[1]中是流量段相同)，保证所有拟合用数据点都在有效拟合区内外，笔者认为还有比较重要的一点是，坐标变换改变了折合流量对压比的拟合系数在不同转速下的变化规律，使其接近线性变化，使得系数的第二步拟合精度提高。

由于拟合区域越大精度越低，故在保证计算需要的前提下应尽量减少拟合的转速范围和各等转速线的压比或流量范围。如需拟合的等转速线的条数过多使拟合精度降低，可以分两个或多个转速区分别进行拟合。

3 评价指标

文献[7]所列的5个评价指标中，残差平方和与均方误差一致，本文选取下列指标评价拟合效果。

(1)相对误差RE

式中：yi为样本值，y̑i为拟合值。RE绝对值越小，拟合效果越好。

(2)均方误差根RMSE

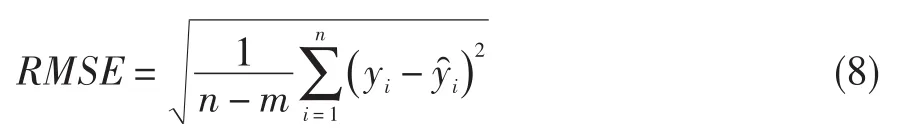
式中：n为拟合时各等折合转速线上选取的工况点的个数，m取1。RMSE越接近0，拟合效果越好。

(3)复相关系数R2

(4)检验指标Q1

(5)检验指标Q2

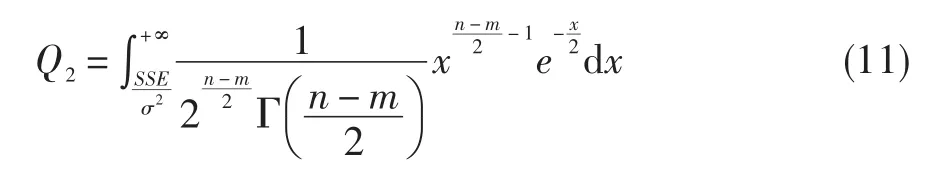
4 压气机流量特性拟合实例

4.1 未经坐标变换的高压压气机流量特性两步拟合

在各等折合转速下，第一步，高压压气机折合流量对压比进行三次多项式(即r取3)最小二乘拟合。未进行坐标变换，将折合流量对压比的拟合系数对转速进行第二步拟合，同样用三次多项式(即tj均取3)，结果见图1。高压压气机流量特性两步拟合曲线见图 2，图中同时显示了 1.020(0表示额定折合转速)等转速线的流量特性拟合结果。图中0.950和0.980等转速线拟合误差较大，1.020等转速线不符合曲线簇形状。可见未进行坐标变换的两步拟合误差较大，且泛化能力差。其原因是图1所示的折合流量对压比的拟合系数在不同转速下变化不规律，系数的第二步拟合误差过大。

图1 未进行坐标变换时高压压气机折合流量对压比的多项式拟合系数对转速的第二步拟合Fig.1 Polynomial coefficients second fitted with the speed which are the ones fitted of the high pressure compressor corrected flow rate with compression ratio without coordinate transformation

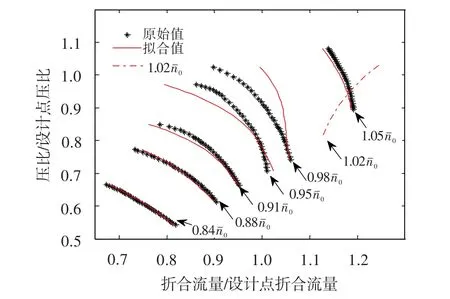
图2 未进行坐标变换的高压压气机流量特性两步拟合曲线Fig.2 Two-step fitting curve of high pressure compressor flow rate without coordinate transformation

4.2 经坐标变换的高压压气机流量特性两步拟合

按第2节中步骤(3)和(4)进行两步拟合，其中0.950曲线作为拟合结果验证而未参与拟合，同时计算了1.020的流量拟合结果。表1列出了两步拟合中不同多项式阶数对应的评价指标值。表中，下标min、max分别表示其他5条等转速线拟合结果的最小和最大值；RE 取绝对值，RE表示 0.950转速线流量拟合的最大相对误差；Q、Q分别表示 0.950曲线的流量拟合Q1和Q2评价指标。由表中可看出，随着拟合阶数的提高，拟合精度随之提高，但当第一步拟合阶数r达到3阶以上时拟合的泛化能力开始变差，表现为 0.950和 1.020曲线变形，如图 3所示。第二步拟合阶数tj均取3阶时相对误差均较大，且Q1偏大、Q2远离0.5，说明拟合精度不够。tj均取5阶比取4阶拟合精度有上升，但提升幅度不大，且可能出现过拟合现象。综上，r取2，tj取4。不同转速下折合流量对进行二次多项式拟合，有：

表1 高压压气机流量特性最小二乘拟合不同多项式阶数的评价指标Table 1 Evaluation indexes of high pressure compressor flow rate fitting using the least square method with different orders

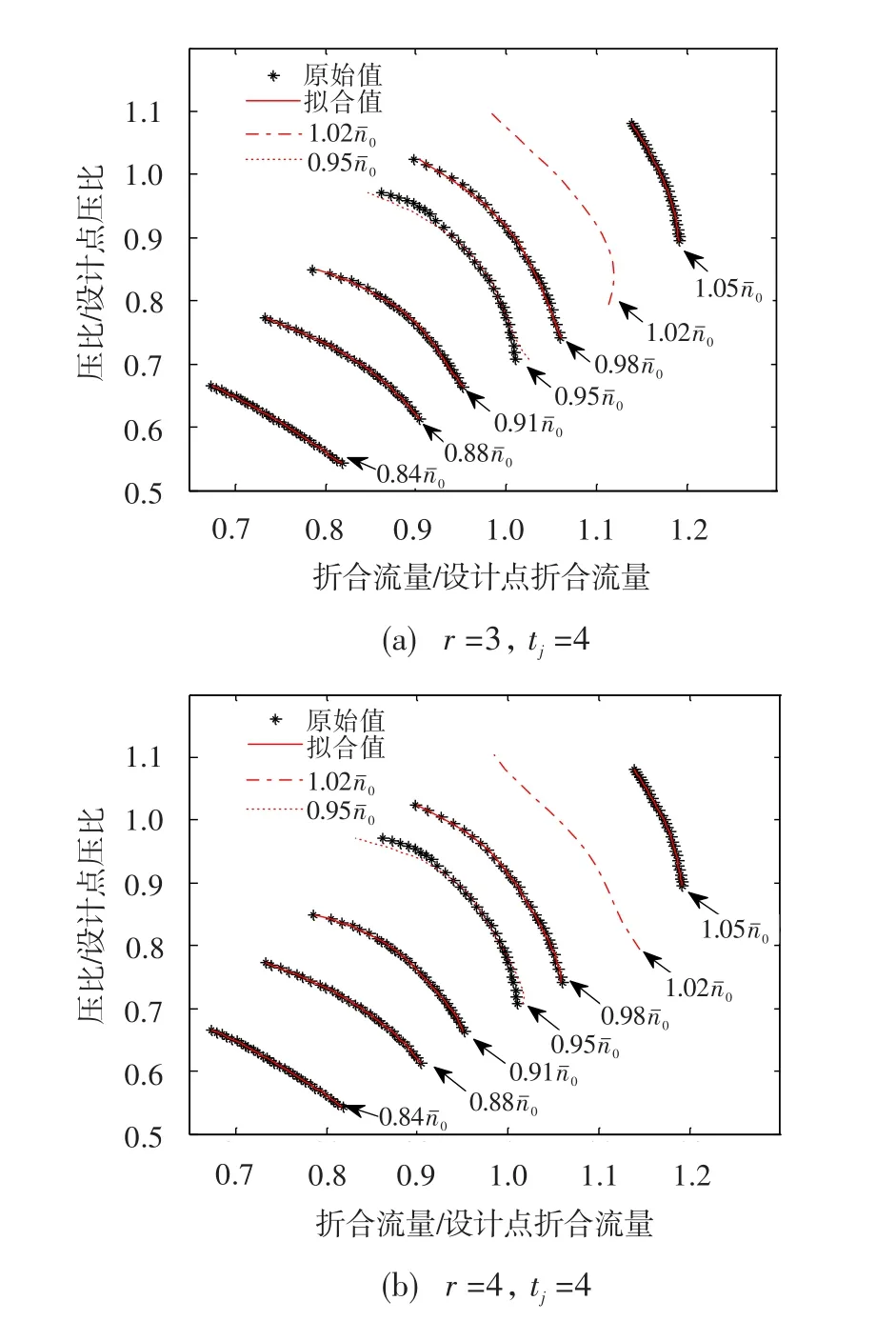
图3 坐标变换后的高压压气机流量特性两步拟合Fig.3 Two-step fitting curve of high pressure compressor flow rate after coordinate transformation

将以上拟合系数用最小二乘法分别对转速进行第二步拟合，结果如图4所示，有：

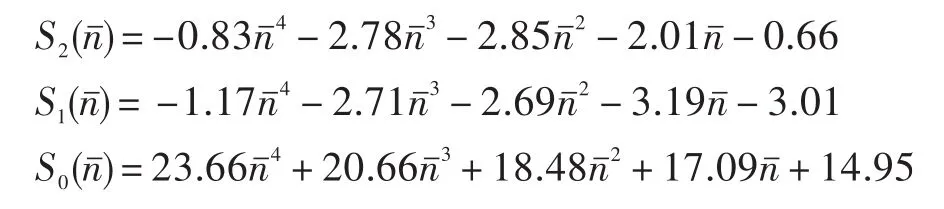
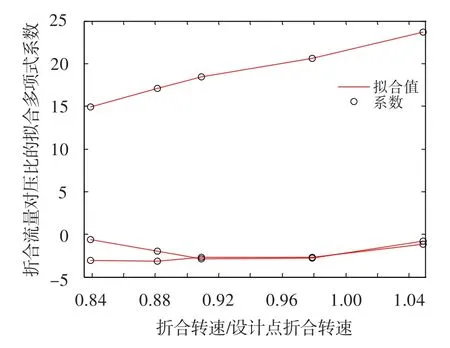
图4 坐标变换后高压压气机折合流量对压比的多项式拟合系数对转速的第二步拟合Fig.4 Polynomial coefficients second fitted with the rotational speed which are the ones fitted of the high pressure compressor corrected flow rate with pressure ratio after coordinate transformation

由图4可知，坐标变换后折合流量对压比的拟合系数变换更接近线性规律，便于进一步精确拟合。故高压压气机流量特性为：

坐标变换后的高压压气机流量特性两步拟合曲线见图 5。图中同时显示了 0.950和 1.020等转速线的流量特性拟合结果，可见其形状符合等折合转速线流量变化规律。两步拟合的折合流量最大相对误差在-1.8%～1.7%之间，大部分误差在±0.5%之内。与一步拟合后误差相比，两步拟合后误差有所增加，不过在可接受范围内，满足工程计算需要。

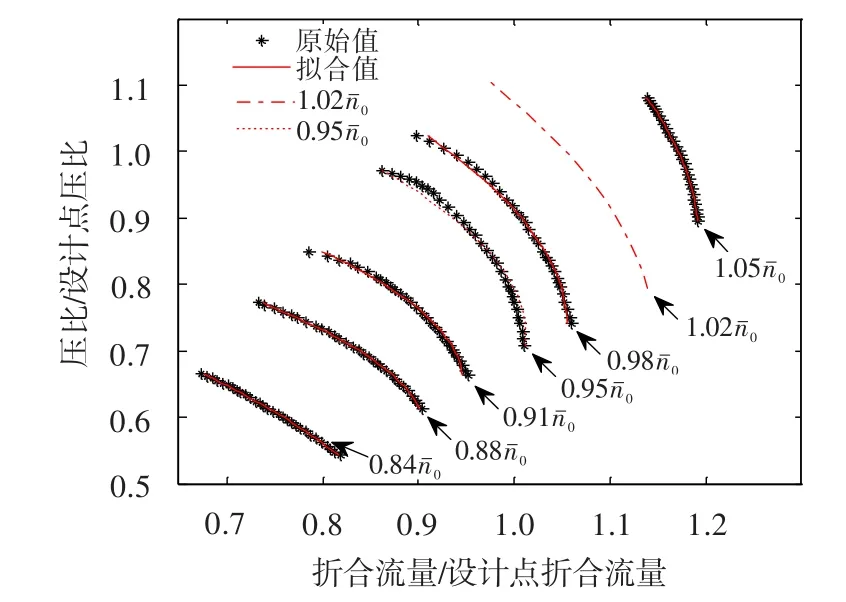
图5 坐标变换后的高压压气机流量特性两步拟合曲线(r=2，tj=4)Fig.5 Two-step fitting curve of high pressure compressor flow rate after coordinate transformation(r=2，tj=4)

4.3 低压压气机流量特性分区拟合

4.4 第二步拟合牛顿插值法与最小二乘法的选择

图6 坐标变换后低压压气机折合流量对压比拟合的多项式系数对折合转速的拟合曲线Fig.6 Polynomial coefficients second fitted with the rotational speed which are the ones fitted of the low pressure compressor corrected flow rate with compression ratio after coordinate transformation

图7 低压压气机流量特性分区两步拟合曲线Fig.7 Two-step partitions fitting curve of low pressure compressor flow rate

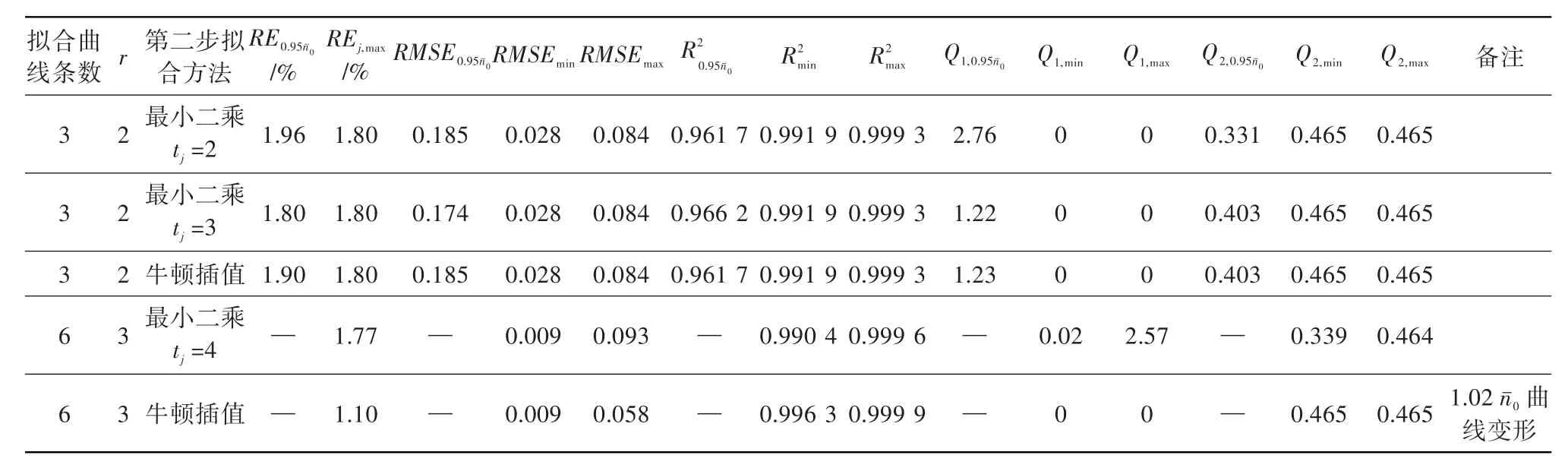
表2 高压压气机流量特性第二步拟合最小二乘法与牛顿插值法的评价指标Table 2 Evaluation indexes of high pressure compressor flow rate fitting with least square method and Newton interpolation method in the second fitting step

拟合3条等转速线时，第一步拟合阶次r取2，第二步采用最小二乘法(tj均取2)和牛顿插值法所得拟合曲线如图 8 所示，图中列出 1.020和 0.950的拟合结果作为检验。由图8和表2可知，需拟合的等转速线较少的情况下，采用牛顿插值函数法与采用最小二乘法的精度相当；由0.950转速线拟合指标相对误差最大值等比较可知，当第二步最小二乘法的阶次为拟合等转速线条数减1时，牛顿插值法精度略优于最小二乘法精度，当然随着第二步最小二乘法拟合阶次的提高，最小二乘法精度会优于牛顿插值法精度。这一结论与文献[1]中在需拟合的等转速线较少的情况下采用构造插值函数法精度较高、采用最小二乘拟合误差会加大的结论不同。

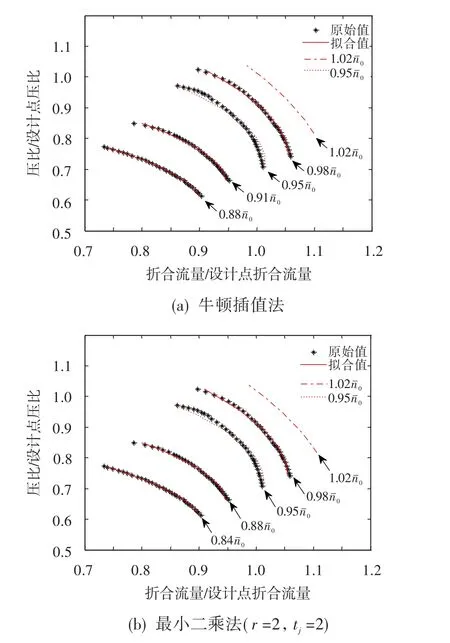
图8 高压压气机流量特性第二步牛顿插值法和最小二乘法拟合曲线(3条)Fig.8 Fitting curves of high pressure compressor flow rate with Newton interpolation method and the least square method in the second fitting step

拟合6条等转速线的高压压气机流量特性时，第一步拟合阶次r取3，第二步牛顿插值法和最小二乘法(tj均取4)所得曲线如图9所示。可见，当拟合的等转速线较多时，牛顿插值法阶次较高，对1.020转速线的拟合曲线有变形，此时最小二乘法泛化能力相对较好，1.020转速线的拟合曲线不至于失真变形。故当需拟合的等转速线较多时牛顿插值法不适用，存在过拟合现象，此时要用最小二乘法。这一结论与文献[1]中的相同。

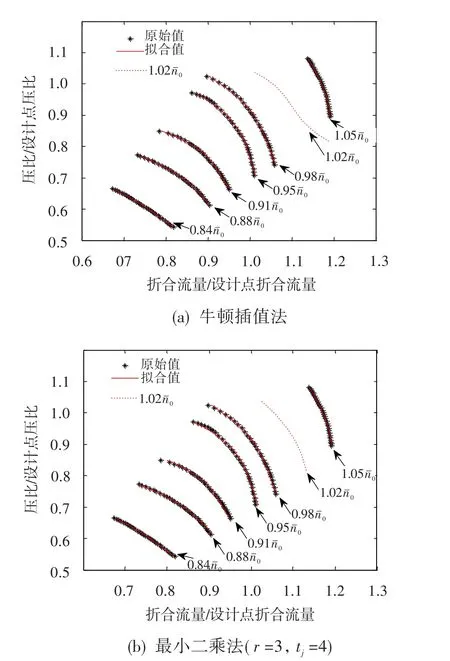
图9 高压压气机流量特性第二步牛顿插值法和最小二乘法拟合曲线(6条)Fig.9 Fitting curves of high pressure compressor flow rate with Newton interpolation method and least square method in the second fitting step

5 结论

提出了先对压比进行坐标变换，后折合流量或效率分两步对压比和折合转速进行拟合的部件特性曲线拟合改进方法。明确了坐标变换的方法，即变换中的参数对转速进行拟合。用多个指标对拟合结果进行了评估，给出了拟合阶次选择方法。列举多个算例验证了该分步拟合方法的可行性。主要结论为：

(1)坐标变换不但保证了所有拟合用数据点都在有效拟合区内，而且还改变了折合流量或效率对压比的拟合系数在不同转速下的变化规律，使其接近线性变化，系数的第二步拟合精度提高。

(2)评价拟合效果除均方根误差等指标外，更重要的是要拟合方程的泛化能力，即未知曲线应符合一致的变化规律。

(3)在保证计算需要的前提下，应尽量减少拟合的转速范围和各等转速线的压比或流量范围。需拟合的等转速线条数过多时，可分两个或多个转速区分别进行拟合，以提高拟合精度。

(4)在第二步拟合过程中，需拟合的等转速线条数较少时，采用牛顿插值函数法与最小二乘法的精度相当；需拟合的等转速线条数较多时，牛顿插值法不适用，应用最小二乘法。