四川盆地超深层高温高压气藏偏差因子及井底流压计算方法优化

杨国红 李 骞 李隆新 胡 蝶 佘 军 阮明龙 聂仁仕

1.中国石油西南油气田分公司勘探开发研究院 2. 西南石油大学“油气藏地质与开发”国家重点实验室

0 引言

下二叠统部署的滚动勘探开发井，均获得高产工业气流，展现了四川盆地西部地区海相碳酸盐岩气藏良好的勘探开发前景[1]。但是高温高压、含硫、超深气藏投入开发，测试安全风险大等难点导致早期产能评价困难，然而产能评价是开发方案中合理配产的依据，因此研究分析高温高压条件下天然气偏差因子计算方法和井底流压计算方法的适应性，用于早期产能评价就具有了重要性。双鱼石茅口组气藏属于高温高压气藏，在开发过程中气藏压力逐渐下降，单井产能，剩余动态储量，井底流压都将发生变化，其中天然气偏差因子计算和井底流压计算方法的准确性将影响到它们计算的准确性，从而间接影响产能评价。目前常用的天然气偏差因子计算方法[2-5]中主要有 BB 法、HY 法、DPR 法、DAK 法、LXF 法、ZGD 法等。井底流压计算方法[6-9]中,常用的主要有平均温度和偏差系数法、Cullender-Smith法、Aziz法和温压耦合模型法。针对双鱼石茅口组气藏高压气藏,根据该气藏的天然气物性，对常用的计算天然气偏差因子的方法进行优选,并改进了温压耦合井底流压计算模型，用于适应该气藏的生产需求。

1 偏差因子计算方法

Berggs 和 Brill于1973 年提出用于计算偏差因子的BB法[10]：

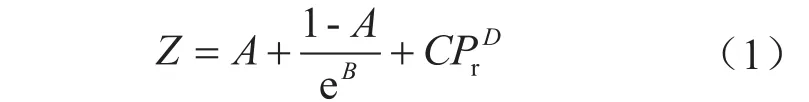
Hall 和 Yarborough于 1973 年根据 Star-ling-Carbahan 状态方程拟合 Standing-Katz 图版得到HY法[11]：

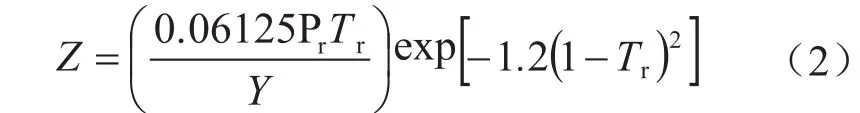
Dranchuk、Purvis 和 Robinson 于 1974 年根据修正 BWR 状态方程拟合 Standing-Katz 图版得到的DPR 法[12]：

Dranchuk 和 Abu-Kassem 于 1974 年 根 据Staring-Carnahan 状态方程拟合 Standing-Katz 图版得到 DAK 法[13]：

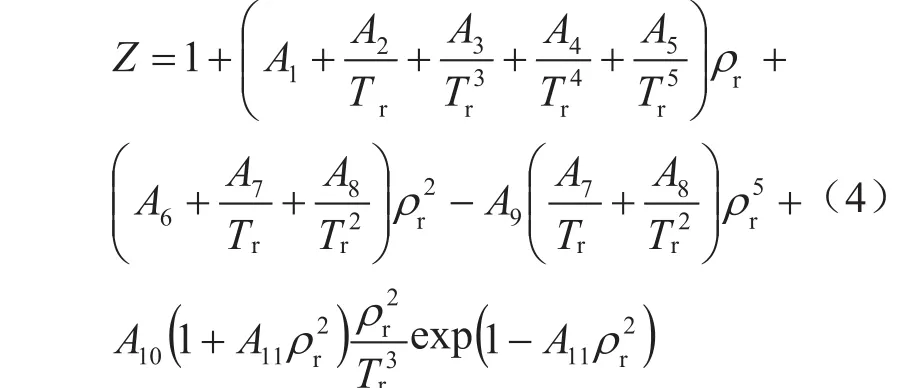
李相方教授于2001 年中国石油大学（北京）根据 Standing-Katz 气体偏差系数图版拟合得解析模型，提出LXF 法[14]：

张国东于2005 年根据 Standing-Katz 图版和Poettmann-Carpenter 的 Z 函数对 LXF 模型各项参数进行修正得到ZGD 法[15]：

其中对比温度和对比压力就可以用下式确定：

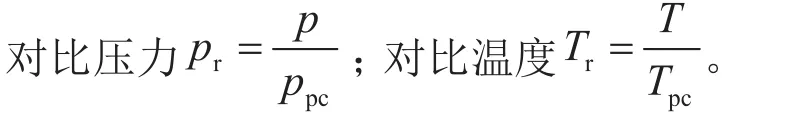
偏差因子适用条件（表1）。

表1 偏差因子计算方法适用条件表

2 井底流压计算方法

1）平均温度和偏差系数计算方法[16]

其井底流压表达式为：

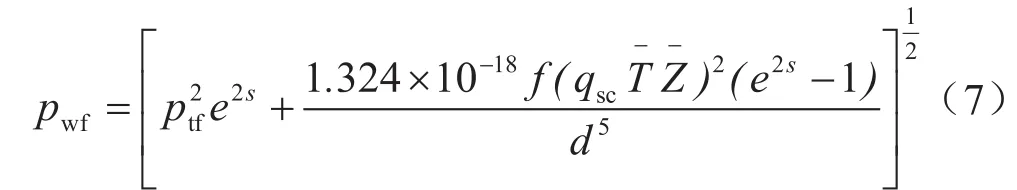
2）Cullender和Smith计算方法[17]

其井底流压积分表达式为：

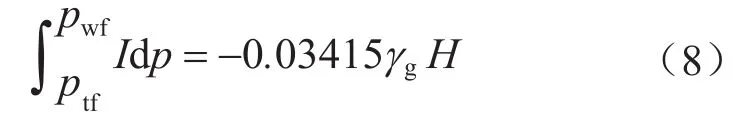
其中：

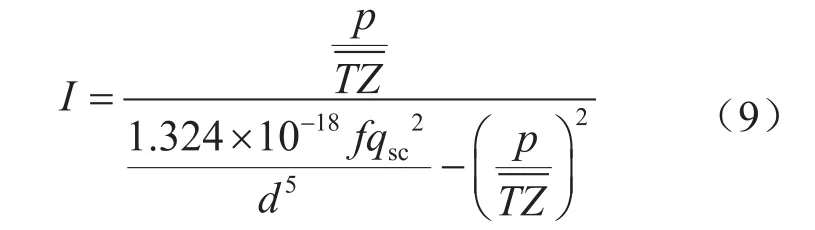
3）Aziz计算方法[18]

其井底流压表达式为：

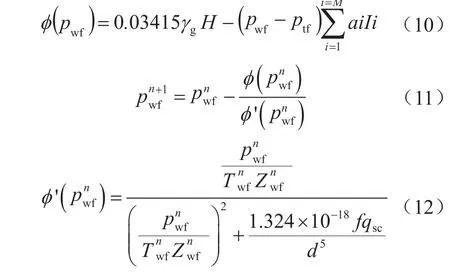
4）温压耦合模型法[19-20]

根据质量守恒方程、动量守恒方程、能量守恒方程和单位长度井段在单位时间内的热损失表达式，来表示为压力、温度、流速和密度的梯度方程组。根据井口处气体的压力（p0）和温度（T0），由状态方程可求出相应的气体密度（ρ0）及流速（υ0）。并以此作为此方程组的边界条件式，即

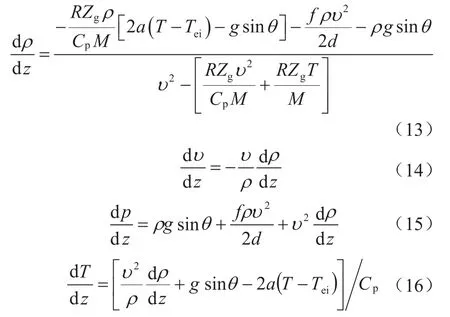
边界条件 ：

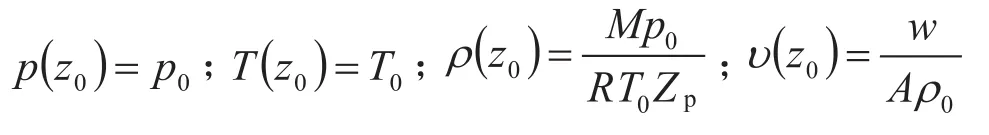
摩阻系数（f）采用Jain公式计算：

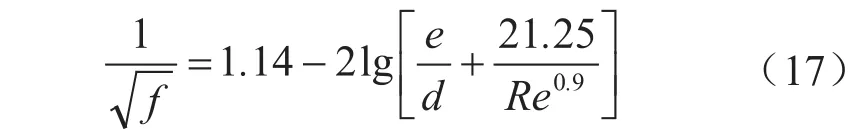
5）改进的温压耦合模型法

温压耦合模型法中对摩阻系数的计算仅采用一种计算方法，可能造成摩阻系数计算达不到全覆盖，从而影响井底流压计算的准确度。因此考虑流态变化对摩阻的影响的基础上对温压耦合模型法进行改进，建立新的计算模型。摩阻系数的计算跟流态有关，流体在管柱中的流动主要分为层流和紊流，紊流又细分为水力光滑，混合摩擦，水力粗糙3种不同的流态。故需要不同的摩阻系数计算公式对流态进行全覆盖用以提高流压计算准确度。首先根据流体雷诺数大小判断流体所在流动区域，再选用相应的公式计算摩阻系数。

对于层流区：

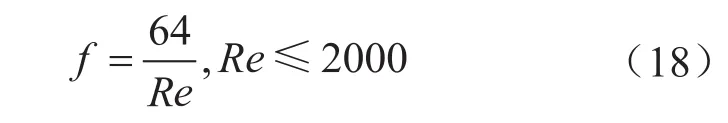
由于层流到紊流的过渡状态极不稳定，没有可靠的公式，一般参照光滑区来选择摩阻系数值。

水力光滑区：

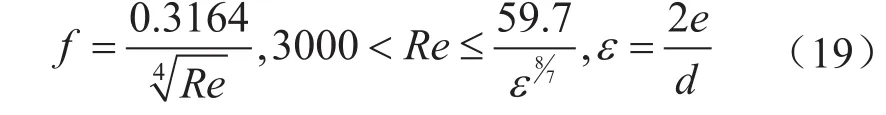
混合摩擦区：

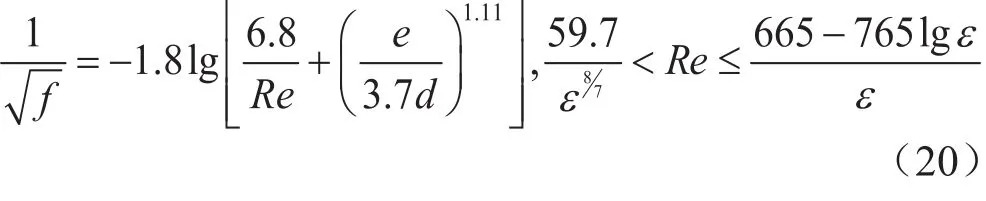
水力粗糙区：

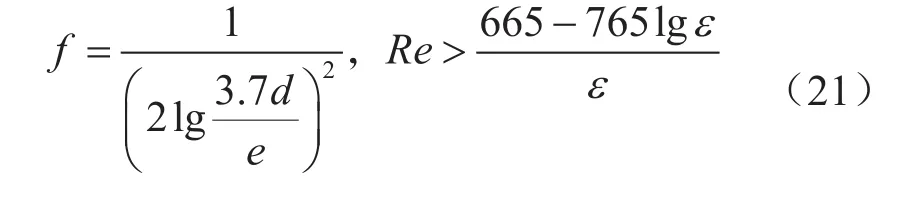
将密度梯度方程（13）、流速梯度方程（14）、压力梯度方程（15）、温度梯度方程（16）和摩阻公式（18）、（19）、（20）、（21）组合在一起，就建立起新的温压耦合模型。

由流动气体的压力、温度、流速和密度组成的方程组，综合考虑井斜角、井身和油管柱结构、井筒径向传热及地层热物理性质等多种因素，沿井深的变化及流态的变化对摩阻的影响采用改进的温压耦合模型进行四阶龙格—库塔法数值求解,可得井筒压力温度分布曲线。

3 计算实例

3.1 基本井况

2016年4月20至2016年4月23日对某井进行稳定试井，最后一个工作制度为22×104m3/d，测得井口压力为63.837 MPa，井口温度25.25 ℃，压力计下入垂深6 350 m,实测稳定流压为82.662 MPa，实测温度为149.55 ℃，实验测得天然气物性参数（表2）。

由于目前产层为茅口组，因此在计算过程中油层套管深度仅取塞面位置，并对井深结构进行适当简化，得到如下井筒物性参数（表3）。

3.2 偏差因子计算方法优选

理论计算与实验值对比（表4、表5）。

从表5中偏差可以看出在压力大于68 MPa后，LXF法计算偏差因子与实测偏差因子偏差大于90%，ZGD法计算偏差因子与实测偏差因子偏差大于1000%，因此表明这两种计算方法不适用于计算该气藏高温高压条件下的偏差因子，其适用范围在33 MPa至68 MPa之间。理论计算偏差系数与实验值间偏差百分比见表6。

将LXF法和ZGD法的计算结果排除后剩余计算方法得到计算结果与实测结果（图1）。

从表6和图1中可以看出，在高压阶段LXF法和ZGD法，最大偏差大于100%，平均偏差大于50%，故不适用于异常高压气藏气体偏差因子计算，BB法、DPR法最大偏差在10%左右，平均偏差在1.5%至3.26%之间，由于最大偏差较大，不推荐用于该气藏气体偏差因子计算。其中HY法和DAK法最大偏差和平均偏差都最低，最大偏差在2.5%左右，平均偏差在0.6%至1.2%之间，能满足工程计算准确性要求，其中DAK法计算偏差最低，故在实际应用，对于该气藏优先推荐DAK法进行计算。

3.3 井底流压计算结果对比

将单井基本物性参数及优选的偏差因子计算方法DAK法代入常规的4种井底流压计算方法及新建立的改进的温压耦合模型，得计算结果（表7）。

平均温度和偏差系数法、Cullender-Smith法、Aziz法只能计算流压，不能计算流温，从计算结果来看，3种方法计算结果相同，与实际测得结果相比，偏差为-3.729%，偏差在工程可接受范围内。而温压耦合模型和改进的温压耦合模型不仅可以计算流压，还可以计算流温，温压耦合模型和改进温压耦合模型计算的结果更接近实测值，其中改进温压耦合模型计算结果更为接近实测值，偏差仅为-1.593%，更具有优越性。因次，在井筒及天然气物性参数齐全的情况下，对于类似气井推荐使用改进的温压耦合模型计算流压，地层物性参数变化较大时，根据实际井况选择相对应参数。

表2 天然气物性参数表

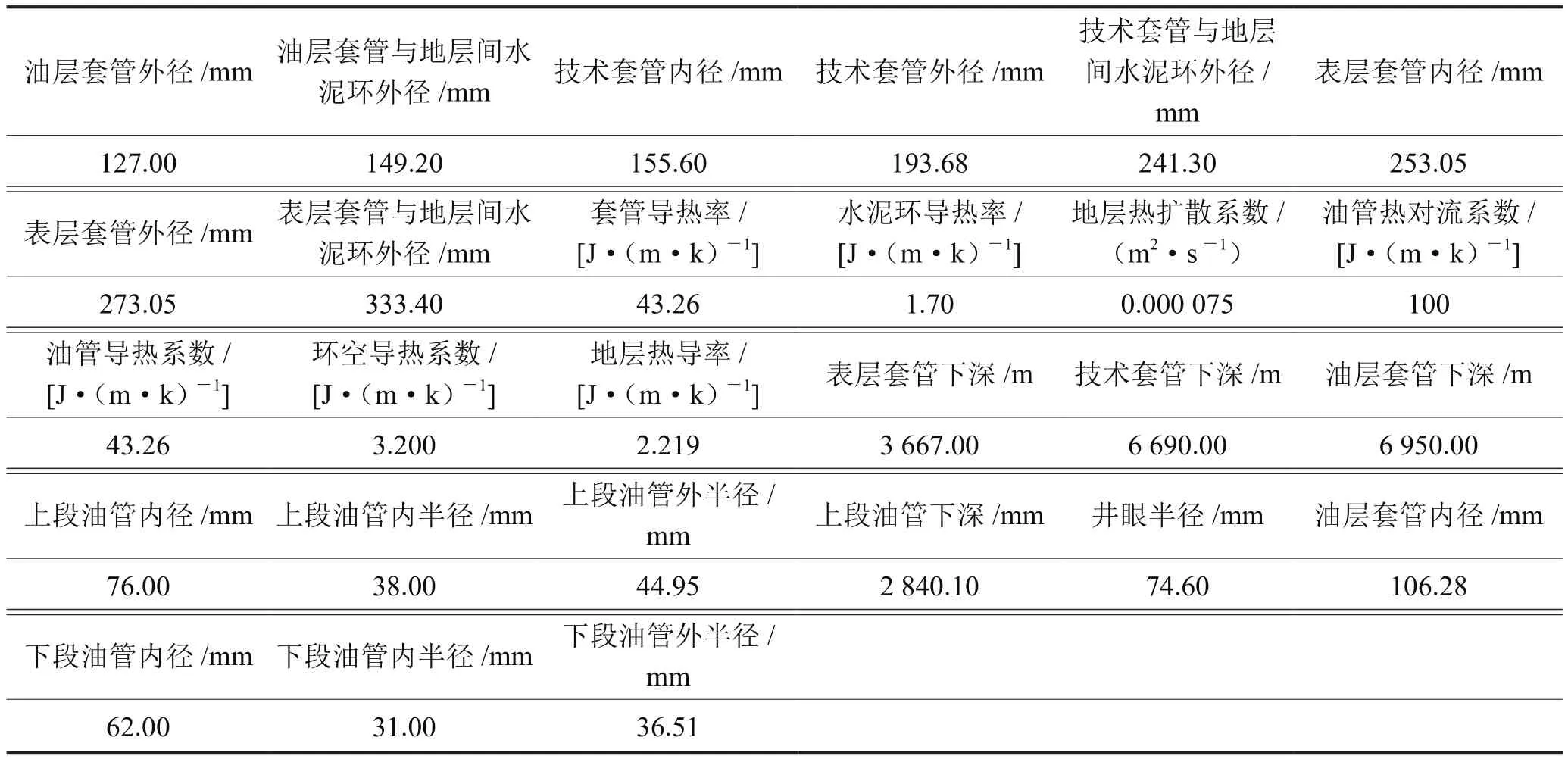
表3 井筒物性参数表

表4 146.7℃时理论计算偏差因子与实验值对比表

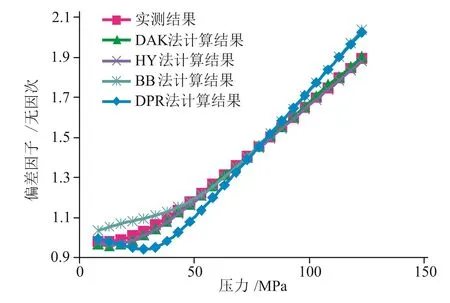
图 1 146.7℃时不同压力下理论与实测偏差因子曲线图

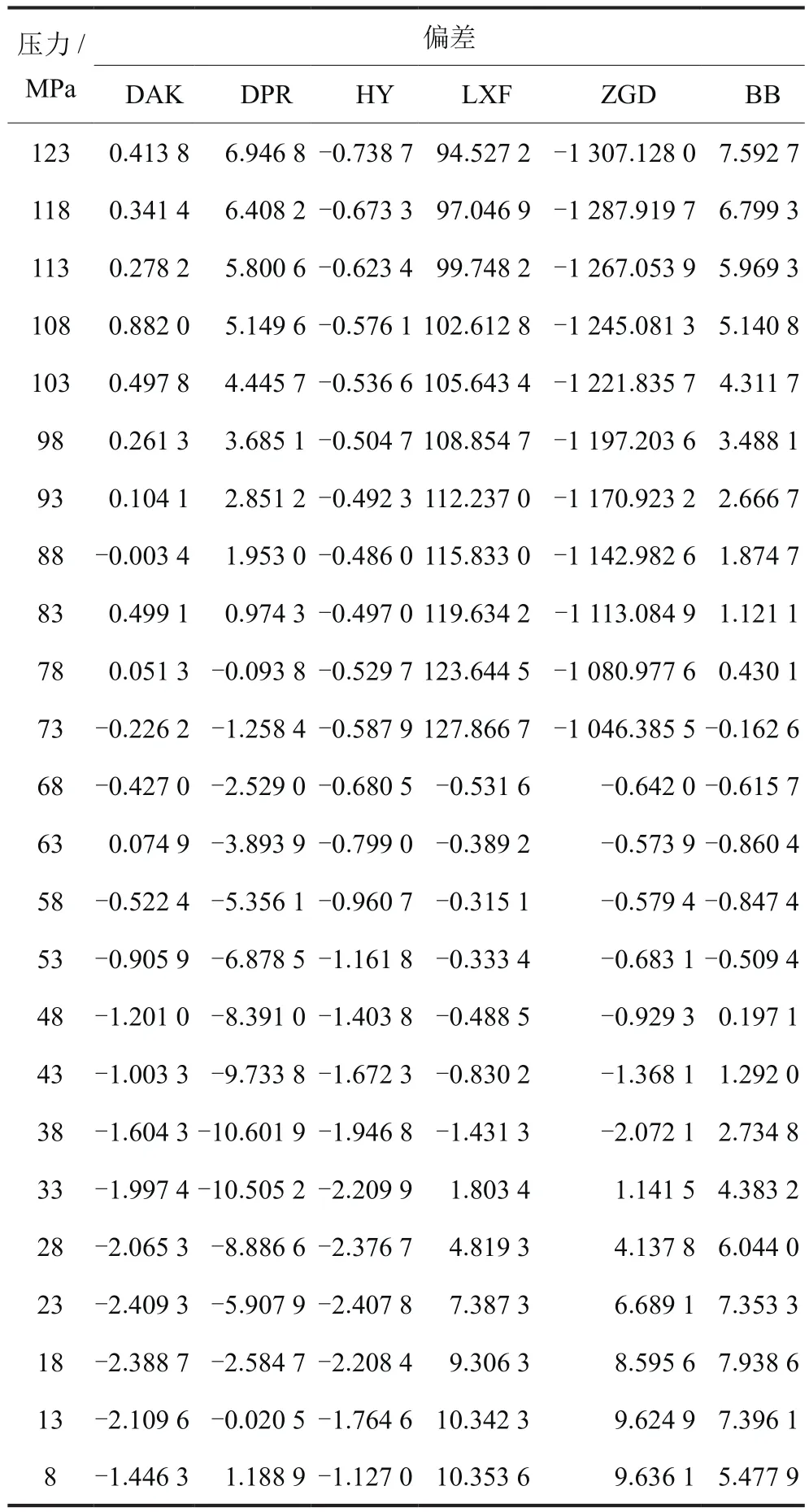
表5 146.7℃时理论计算偏差系数与实验值间偏差表

4 结论

1）研究表明LXF法和ZGD法适用范围为33 MPa至68 MPa之间，不适用于该气藏高温高压条件下天然气偏差因子的计算。

2）研究表明，针对该气藏的天然气物性，在高温条件下HY法和DAK法在8 MPa至123 MPa压力范围内都能适用，适应性广，计算准确性高。

3）对于该气藏，井底流压计算结果表明改进的温压耦合模型计算结果最接近实测值，偏差仅-1.593%。

4）针对同类气藏，在计算天然气偏差因子时，建议优先考虑DAK法和HY法，计算高温高压井底流压时，优先考虑采用改进的温压耦合模型法进行计算。

表6 理论计算偏差系数与实验值间偏差范围表

表7 理论计算方法计算结果与实测结果对比表

符 号 说 明

p表示气体压力/MPa；T表示气体温度/K；pr表示对比压力，无因次；Tr表示对比温度，无因次；pwf表示井底流压/MPa；ptf表示井口流压/MPa；d表示 油管内径/m；T表示油管内气体平均温度/K；Z表示在T、p条件下，气体偏差系数，无因次；qsc表示标准状态下气体的流量/（sm3/d）；f表示摩阻系数，无因次；e表示粗糙度/m； ；γg表示气体相对密度，无因次；H表示油管下到气层中部深度/m；d表示油管内直径/m；Re表示雷诺数，无因次； kcas表示套管导热率/（J/m·k）；kcem表示水泥环导热率/（J/m·k）；α表示地层热扩散系数/（m2/s）；ht表示油管热对流系数 /（J/m·k）；kt表示油管导热系数 /（J/m·k）；hc表示环空导热系数 /（J/m·k）；ke表示地层导热率 /（J/m·k）；tD表示无因次时间；Cp表示定压热容/（j/kg.k）；Tei表示初始地层温度/K；Ts表示地面温度/K；gt表示初始地温梯度/（K/m）；A表示油管截面积/m2；M表示分子量/（kg/mol）。