基于辨识矩阵的多伴随模糊粗糙集属性约简

梁 美 社

(石家庄职业技术学院 科技发展与校企合作部，河北 石家庄 050081)

粗糙集理论是20世纪80年代波兰学者Pawlak教授提出的，主要用于处理关系数据库中不完备、不精确的信息[1-2].当前，粗糙集理论被广泛应用于工业控制[3-4]、生物医学[5-6]、市场预测[7]、图像处理[8-9]等领域.

早期粗糙集理论的经典著作主要利用一些等价关系，来处理数据集中对象关于属性取值为特殊离散值的情况.等价关系的交集仍是等价关系，Pawlak将其称为不可辨识关系[1-2].因为等价关系的要求过于严苛，因此在实际应用中往往受到很大的限制.在过去的20年中，针对不同的问题，学者们对等价关系进行了多种形式的推广，如优势关系[10-11]、容差关系[12-13]、模糊关系[14-16]和相容关系等.

1965年，Zadeh教授提出了模糊集的概念[17].粗糙集与模糊集都是处理不确定性信息的重要工具，也是研究信息系统中知识不完全、不确定问题的重要方法.将粗糙集中被近似的经典集合扩展到模糊集合，将等价关系推广到模糊关系，就得到了模糊粗糙集的概念[18].后来，一些学者进一步把经典逻辑算子推广为模糊逻辑算子[19-24].而多伴随算子的运用，使其理论发展到了一个全新的阶段.

现有的多伴随模糊粗糙集模型[25]中，通过定义模糊测度，得到的属性约简均为水平α下的近似约简.本文拟在多伴随模糊粗糙集模型的基础上，通过构造属性约简的可辨识矩阵，给出属性约简的计算方法和相关性质，进而得到模糊决策信息系统的精确属性约简.

1 预备知识

1.1 粗糙集理论

经典粗糙集理论[1]中，信息系统通常表示为IS=(U,Α)，其中对象集合U={x1,…,xn}，属性集合Α={a1,…,am}，是非空有限集.对于∀a∈Α，定义映射fa:U→Va，其中Va是属性a在U上的值域. 对于B⊆A，记为RB={(x,y)∈U×U:∀a∈B,fa(x)=fa(y)}，则RB是由属性集合B确定的U上的等价关系. 由RB可以得到U上的一个划分.U/RB={[x]B:x∈U}，其中[x]B={y∈U:(x,y)∈RB}.

对于X⊆U，它关于RB的下、上近似分别为:

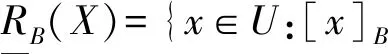
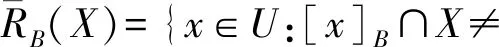
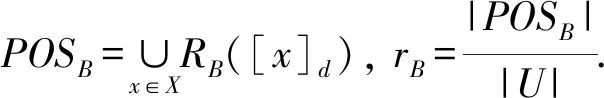
若rA=1，称(U,Α∪{d})为一致的决策信息系统. 若POSB=POSA，且∀B′⊂B，有POSB′≠POSA，称B为A的决策约简.

经典粗糙集中，另一种求属性约简的方法是基于可辨识矩阵和辨识函数的.

决策信息系统(U,Α∪{d})的辨识矩阵O是一个(n×n)阶矩阵，具体定义为：

其辨识函数定义为f(U,RA)=∧{∨Oij}(i≠j).由辨识函数计算得到的最小析取范式，即为该决策信息系统(U,Α∪{d})的所有约简.

1.2 多伴随模糊粗糙集理论

多伴随模糊粗糙集是对粗糙集理论的一种推广.通过引入一组伴随对来计算模糊集的上下近似.不同伴随对的使用表达了研究者对不同对象的偏好.这种推广极大地增强了粗糙集理论的应用.

定义1[21]设(P1,≤1)，(P2,≤2)，(P3,≤3)为三个偏序集，定义映射:P1×P2→P3， ↙:P3×P2→P1，↖:P3×P1→P2，若对于任意x∈P1，y∈P2，z∈P3，满足:

(1)x≤1z↙y当且仅当x&y≤3z，当且仅当y≤2z↖x;

(2)&对两个参数是单调增的;

(3)↙,↖对第一个参数单调增，对第二个参数单调减;

(4)称(&,↙,↖)是关于P1,P2,P3的伴随三元组.

常用的有Godel，product，ukasiewiczt-模及其蕴含算子构成的伴随三元组，它们分别定义[21]为：

x&Py=x·y,z↖Px=min{1,z/x};

x&Ly=max{0,x+y-1},

z↖Lx=min{1,1-x+z}.

假设(U,Α∪{d})为模糊决策信息表，(P,≤)为一偏序集，TP为P中最大元素，对于∀a∈A，定义映射Ra:U×U→P为P-模糊容差关系，使其满足自反性，即对于∀x∈U，有Ra(x,x)=TP;使其满足对称性，即∀x,y∈U，有Ra(x,y)=Ra(y,x).

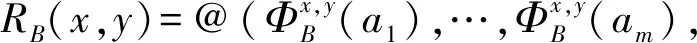
在多伴随面向属性框架下，考虑形式背景(U,U,RB,τ)，对于∀x,y∈U，定义似然算子和必然算子:

g↑π(x)=sup{RB(x,y)&τ(x,y)g(y)|y∈U}，

f↓N(y)=inf{f(x)↖τ(x,y)RB(x,y)|x∈U}.

g↑π是g的上近似，f↓N是f的下近似.{(&τ(x,y),↙τ(x,y),↖τ(x,y)为伴随对集合，其中τ:U×U→I表示将任意一对对象映射为某一特定的伴随对，I为一指标集.

定义3[24]对于给定模糊子集h∈LX，(h↓N,h↑π)称为多伴随模糊粗糙集.

在模糊决策信息表(U,A∪D,f,V)中，D={d}为决策属性，利用必然算子定义多伴随模糊粗糙集正域，对于∀y∈X，

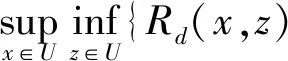
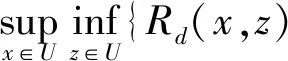
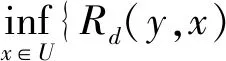
文献[25]中利用模糊蕴含和模糊基数来定义正域依赖度，通过模糊蕴含算子来定义L-测度.

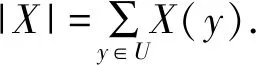
由定义4可以得到，模糊决策信息表(U,A∪D,f,V)中属性子集B的正域依赖度为：

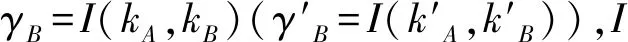
定义6[24]设γ:Ρ(Α)→L是决策系统(U,Α∪{d})的一个L-测度，B⊆Α且α∈L，若γ(B)≥α，α≠⊥L则称B是一个α水平下L-决策超约简.若对于∀B1⊂B，有γ(B1)<α，则称B是一个α水平的下L-决策约简.

显然，这个约简与参数α的取值密切相关.给定α后，其得到的约简均为近似约简.

2 基于辨识矩阵的模糊正域约简

在定义2中，模糊不可辨识关系是通过一个单调聚合算子得到的.而在经典的粗糙集理论中，对于属性子集B⊆A，其等价关系为RB=∩a∈BRa.本文将借鉴这个思路，给出新的模糊不可辨识关系的定义.

为了方便讨论问题，本文的模糊信息决策表为(U,A∪D,V,f)，其中，|U|=n，|A|=m，D={d}，且决策属性为经典的明确关系.

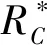
证明由定义7可直接得到.

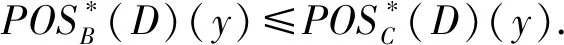
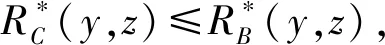
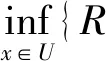
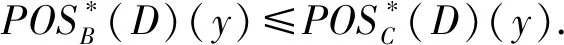
如果保证模糊正域不变，则可得到属性约简定义8.

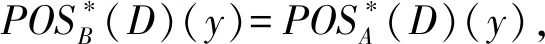
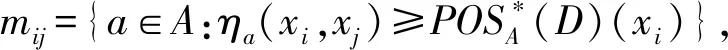
定义9给出了利用辨识矩阵求解模糊决策约简的方法.

定理3设(U,A∪D,V,f)为一模糊决策信息表，属性子集B⊆A，B∩mij≠Ø(i≠j,i,j≤n)，则B是一个模糊正域协调集.

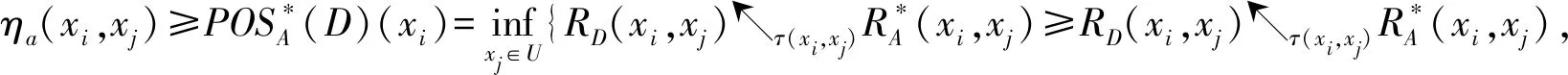
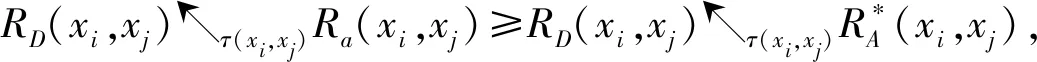
定理4设(U,A∪D,V,f)为一模糊信息决策表，MF为其辨识矩阵，有以下性质：

(1)mii=A，i≤n；

(2)若a为核心属性，当且仅当存在i,j≤n时，

(3)使得mij=a.

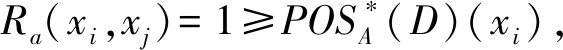
(2)设a为核心属性，若任意包含a的可辨识属性集mij(i≠j)中至少含有两个元素，令B=∪i≠j(mij-{a})，则B∩mij≠Ø(∀i≠j).由定理3可知，B是一个模糊正域协调集，因而存在C⊆B使得C为一个模糊正域约简.显然a∉C，这与a为核心属性矛盾.

反之，设mi0j0={a}，∃B⊆A(a∉B)为一个模糊正域约简，则B是一个模糊正域协调集，由定理3可知，B∩mij≠Ø(i≠j,i,j≤n)，这与B∩mi0j0≠Ø矛盾，故若B为一个模糊正域约简，均有a∈B，由核心属性定义可知，a为核心属性.

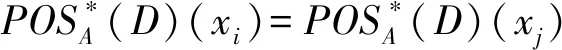
定义10设(U,A∪D,V,f)为一模糊决策信息决策表，MF为模糊决策信息表的可辨识矩阵，定义fF(U,RA)=∧{∨mij}，其中i≠j.称fF(U,RA)为(U,A∪D,V,f)上的记辨识函数.

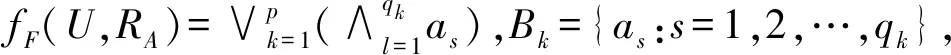
证明根据定义9、定理3和最小析取范式的定义即可证得结论.

所有约简集合的交集称为核心属性，记为CoreF(A).

3 实例分析

例1设属性集A={a1,a2,a3,a4}，决策属性集合D={d}，对象集U={x1,x2,…,x7}，映射f:U×A→V，模糊决策表(U,A∪D,V,f)如表1所示.

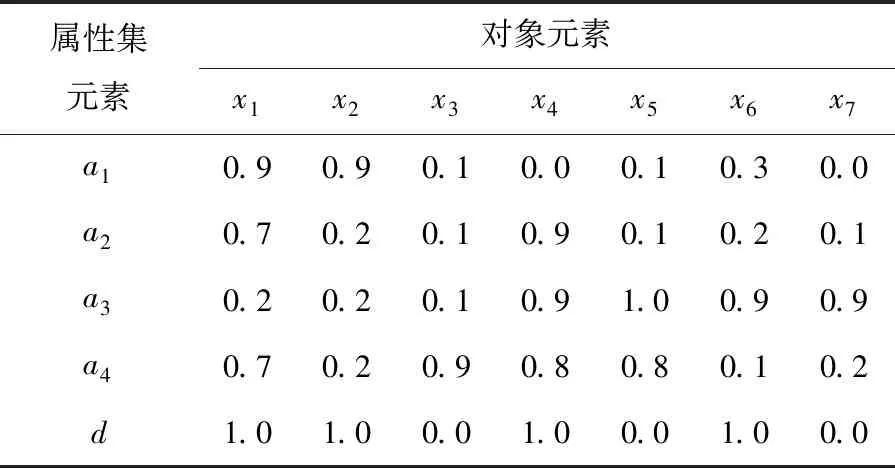
表1 模糊决策表(U,A∪D,V,f)

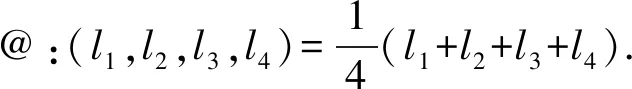
同样的方法，可以得到A的所有子集的模糊容差关系矩阵.令

由此计算出关于所有属性子集的直觉模糊正域依赖度如下：

kA=0.91,k{a1,a2,a4}=0.90,k{a1,a2}=0.81,k{a2,a4}=0.76,k{a1,a2,a3}=0.84,k{a1,a3}=0.36,k{a2,a3}=0.71,k{a1,a3,a4}=0.85,k{a2,a3,a4}=0.84,k{a3,a4}=0.75,k{a1,a4}=0.80,k{a1}=0.30,k{a2}=0.61,k{a3}=0.19,k{a4}=0.46.

令I=↖L，根据定义5有，γA=1,γ{a1,a2,a4}=0.99,γ{a1,a2}=0.90,γ{a2,a4}=0.85,γ{a1,a2,a3}=0.93,γ{a1,a3}=0.45,γ{a2,a3}=0.80,γ{a1,a3,a4}=0.94,γ{a2,a3,a4}=0.93,γ{a3,a4}=0.84,γ{a1,a4}=0.89,γ{a1}=0.39,γ{a2}=0.70,γ{a3}=0.28,γ{a4}=0.55.

若α=0.95，则B={a1,a2,a4}为L-决策约简；若α=0.90，则{a1,a3,a4,a2,a3,a4,a1,a2}为L-决策约简.

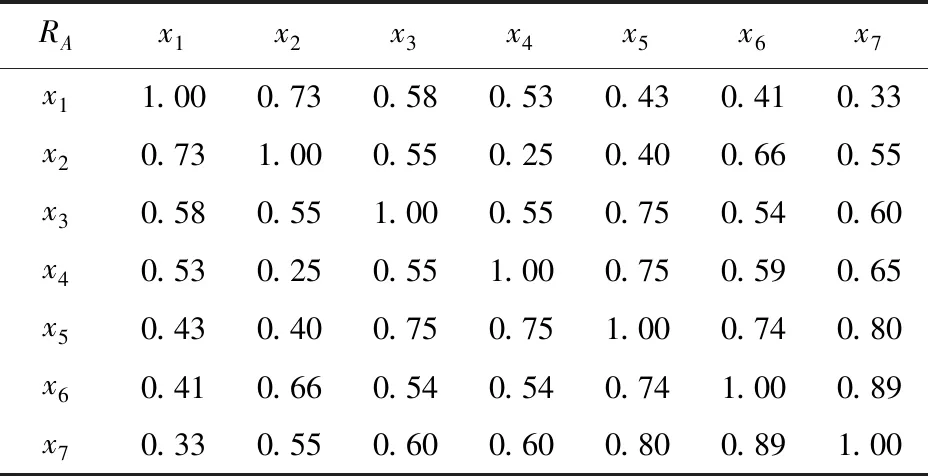
表2 属性集合A的模糊容差关系矩阵

例2例1中的模糊决策表(U,A∪D,V,f)，根据定义7，可得到属性集合A的新模糊不可辨识关系矩阵，见表3.

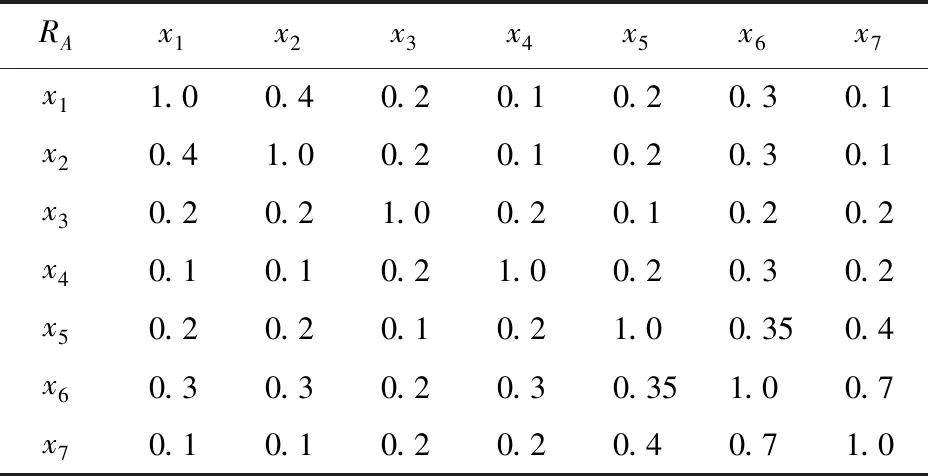
表3 属性集合A的新模糊容差关系矩阵

根据定义9，可得到模糊信息决策表(U,A∪D,V,f)的辨识矩阵MF如表4. 由定义10中辨识函数计算公式可知，B={a1,a2,a4}为模糊信息决策表(U,A∪D,V,f)的一个约简.a1,a2,a4均为核心属性.

表4 辨识矩阵

利用模糊L-测度求解模糊信息决策表约简时，最坏的情况是，先求出所有属性子集所对应的模糊关系矩阵，然后再求各个关系矩阵下的模糊正域，其计算时间复杂度应不小于o(2n·(m+n)n2)；利用辨识矩阵求解约简时，不需要求解所有属性子集的模糊关系矩阵及相应模糊正域，在最坏情况下的时间复杂度为o((3m+n)n2). 因此，辨识矩阵方法在求解约简时可大大降低时间复杂度.

4 结语

通过实例对比分析可知，本文提出的利用辨识矩阵求解多伴随模糊粗糙集属性约简具有以下性质：所求约简集合为模糊决策信息系统的精确约简集合；简化了属性约简的计算过程，有利于提高知识的获取效率.