基于GA-SLFRWNN的空中目标威胁评估

陈侠, 刘子龙, 梁红利

(沈阳航空航天大学 自动化学院, 辽宁 沈阳 100136)

随着战争中信息化的飞速发展,实时而准确地评估目标威胁,不仅为空战决策提供科学的决策依据,而且能够提高杀伤概率,因而研究目标威胁评估问题具有重要的理论和实际意义。针对空战中目标威胁评估系统非线性、评估难度大且富含不确定信息的问题,建立有效的评估威胁系统是很困难的。目前关于威胁评估模型及方法已经得到了广泛的研究。主要技术为:直觉模糊集[1-4]、贝叶斯推理[5-6]、多属性决策法[7]、优劣解距离法[8]、计划识别[9]等。上述方法在很大程度上是依据专家经验确定威胁指标权重,具有较强的主观性,很难精确映照出威胁因素间的复杂非线性函数。在预测领域,神经网络凭借良好的自学习、自组织能力得到了广泛的应用[10-12]。文献[10]运用优化的BP(back-propagation)神经网络对目标评估问题进行分析,表明了神经网络解决评估问题的有效性。但是,BP神经网络存在易陷入局部极值、过学习以及泛化性能差等问题。文献[12]研究了基于模糊控制系统的稳定性问题,文献[11]采用模糊推理系统结合BP神经网络对空中威胁进行了研究,其优点在于可以解决目标威胁环境中存在的模糊及不确定的问题。虽然模糊神经网络(fuzzy neural network, FNN)已经成功地应用于许多复杂问题,但依然有2个缺点：①模糊神经网络存在着依赖先验知识、抗干扰性差、推广能力不足等问题；②神经网络的性能往往取决于网络参数的选取,因此对于初始参数的选取就显得至关重要。为了解决上述2个问题,本文应用单隐含层模糊递归小波神经网络对目标威胁评估模型进行建模。SLFRWNN是将递归小波神经网络放入模糊神经网络的后件部分用于存储网络先前数据,相比于模糊神经网络,新模型能增强复杂系统的计算能力和泛化能力。遗传算法是一种用于对连续搜索空间进行智能寻优、二进制编码表示的优化技术,具有搜索速度快、效率高等特点。因此,为了提高神经网络的性能,采用遗传算法对网络的初始参数进行优化选取。在参数优化过程中,梯度下降法中的学习率选取往往影响网络的收敛速度,以往常常采用固定学习率对参数进行更新,通常依据专家经验进行选取,很难找到一个较好的学习率。本文采用一种自适应学习率,快速修正参数,使网络输出不断逼近期望输出,仿真实验表明:相比于FNN和FRWNN,该算法提高了系统的稳定性,加快了收敛速度,增强了预测精度。

1 SLFRWNN模型

TSK模糊模型相对于Mamdani模糊推理系统具备如下优点:对动态输入的改变具有较好的敏捷性,较少的处理时间,较高的精确性和鲁棒性。然而,当传统的TSK模糊模型的后件部分被具有大量神经元的WNN代替时,TSK模糊模型对输入的改变所需的反应时间增加了。因此,本文提出一种使用单隐含层递归小波神经网络结构嵌入进TSK模糊模型的后件部分,简称SLFRWNN。网络的后件部分是通过使用具有存储网络过去数据能力的单层神经元构成的。由于小波函数具有良好的时-频两域定位特性,这种结构不仅保持了TSK模糊模型的后件部分的简洁性,同时也增加了网络的计算能力和收敛能力。假设有Nr个模糊IF-THEN规则:

(1)

式中,xi是模型的第i个输入(i=1∶Nin),Aij是以模糊隶属度函数μAij(xi)(j=1∶Nr)为特征的语言项。具有Nin个输入和Nr个模糊规则的SLFRWNN结构如图1所示。

图1 SLFRWNN结构

第一层的输入直接传递给第二层。第二层包括模型输入的隶属度函数,每个节点的输出计算为

∀i=1∶Nin;j=1∶Nr

(2)

式中,cij是第j个规则中隶属度函数的中心参数,σij是伸缩参数。第三层每个节点代表一个模糊规则R,因此,第三层节点数等于规则R1到RNr的个数。每个节点输出描述为

j=1∶Nr, 0<μj<1

(3)

生成层的小波神经元产生的结果计算方程式中∏代表取小运算。第四层代表模糊规则的后件部分,是将小波函数作为激活函数的单隐含层网络构成。

通过使用小波变换在多个分辨率等级上捕获有用的信息,模型的学习能力得到了显著增强。由于选取不同的母小波函数,则对模型性能产生不同的影响。所以本文通过对比3种类型的母小波激活函数,进行研究分析:

1) Gaussian wavelet:

(4)

2) Mexican Hat wavelet:

(5)

3) Morlet wavelet:

(6)

这些小波函数如图2所示。

图2 Gaussian,Mexican Hat和Morlet简化图

第四层每个小波φij都是根据选定的激活函数的母小波经过伸缩平移变换的形式,表达式为

φijφij(zij(k))=((uij(k)-tij(k))/dij(k))

∀i=1∶Nin,j=1∶Nr

(7)

对于离散时间k

uij(k)=xi(k)+φij(k-1)θij(k),

i=1∶Nin,j=1∶Nr

(8)

式中,tij和dij分别代表小波函数的平移系数和伸缩系数;θij是递归回环的权重,称为储备系数。下脚标ij表示第j个规则对应的第i个输入。

∀i=1∶Nin,j=1∶Nr

(9)

第四层的输出结果为

vj(k)=wj·ψj,j=1∶Nr

(10)

式中,wj是生成层和输出层之间的连接权值。第五层每个节点的输出等于第四层的输出乘第三层节点的输出。这一层的输出表达式为

(11)

式中

(12)

模糊规则后件部分输出由公式(10)计算得到。最终,第五层输出层的总输出结果是每个规则产生结果的累加和,计算公式为

(13)

式中,u(k)是由所提出的6个参数(cij,σij,wj,θij,tij,dij)构成的模型输出。网络设计的目的是确定这些参数的最优值。

2 GA原理

神经网络的收敛速率取决于对被优化参数初始值的选取,因此,本文应用基于GA的方法初始化SLFRWNN。在处理连续搜索空间时,真实编码的遗传算法具有优于二进制表达的优势,因此,运用基于真实编码的遗传算法优化技术寻找网络参数的最优解。在网络初始化过程中,前件隶属度函数的中心参数cij和伸缩参数σij,小波函数的转换和伸缩系数tij和dij,存储系数θij,后件部分的权值wj是需要被优化的。假设有Ns个样本(x(1),x(2),…,x(k),…,x(Ns)),SLFRWNN初始化取决于期望的输出ud(k)和网络输出u(k)的误差的最小值。因此,第k个样本中第q个染色体的适应度函数为

(14)

式中,uq(k)是对应于第q个染色体的网络输出值,其表达式为

(15)

式中

(16)

所以,第q个染色体表示为

∀i=1∶Nin,j=1∶Nr

(17)

式中

通过GA方法对问题的解空间进行全局搜索,使得种群中对应最小适应度函数值的最优染色体决定网络参数的初始值。

3 SLFRWNN反向传播学习算法

本文采用基于微分链式法则的反向传播学习算法调整所有参数。基于单隐层结构改进的网络在实时操作中具有快速训练过程,并且在此过程中表现出对变化量的快速反应。学习过程的目的是使误差平方和函数最小:

(24)

ud和u分别代表离散时间k时刻网络的期望输出和实际输出。所有后件部分的参数如wj,tij,dij,θij(i=1∶Nin,j=1∶Nr),使用下面的公式进行调整:

∀i=1∶Nin,j=1∶Nr

(25)

式中，γ为学习率并且大于0,Nin是网络输入变量的个数,Nr是规则数目。(25)式中的偏导数变量表示为:

根据公式(25)～(31)更新参数,使得目标函数E(k)达到最小。

4 最优学习率

网络训练过程中,学习率起着至关重要的作用。一方面,如果学习率过小,算法需要很长时间才会收敛,另一方面,学习率取较大的值就会造成训练过程不稳定。为了解决上述问题,本文通过Lyapunov稳定性理论得出最优学习率。最优学习率不仅保证学习过程的收敛性,同时也能加速网络的学习过程。网络输入输出表示如下:

(32)

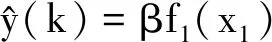
(33)

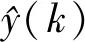
(34)

定义Lyapunov函数为

(35)

变化量为

(36)

由下式

可得:

(37)

误差的改变量为

(38)

式中

(39)

(40)

由公式(38)～(40),可得Δe(k)为

(41)

由公式(37)～(41),则将ΔV(k)表示为

化简为

式中

由Lyapunov稳定性理论可知,如果ΔV(k)<0,系统是稳定的。由于∀j=1∶Nr,则有μj(x)≤1,所以当γ(k)满足(42)式时,则保证网络的收敛性。

(42)

5 空中目标威胁的主要因素

威胁评估系统具有非线性、评估难度大且富含不确定信息等特点。本文采用G A Miller的量化原理和归一化对不确定信息进行量化处理[13],考虑的影响因素主要有:对方目标的态势信息、对方目标的作战性能等诸多因素。本文主要考虑了6种典型指标,分别为:

1) 目标种类:分5大类:导弹、直升机、小型目标、大型目标和TBM。采用G A Miller的量化原理对其量化,得到对应的隶属度μ值为0.1,0.2,0.3,0.4,0.5;

2) 目标干扰能力:分为很强、强、一般、弱、很弱5个等级。对应依次量化为0.9,0.7,0.5,0.3,0.1;

3) 目标航向角:在0°～360°中,按照36°进行划分。对应其μ值分别为0.9,0.8 0.7,0.6,0.5,0.4,0.3,0.2,0.1,0;

4) 目标高度:分为4个等级。按照μ分别是0.2,0.4,0.6,0.8,对应是高、中、低、超低;

5) 目标距离:其μ值按着如下公式进行计算:

6) 目标速度:其μ值按着如下公式进行计算:

针对上述6种指标,构建基于SLFRWNN的威胁评估模型。表1为目标威胁数据库[10]中的部分数据。从该库中,随机采用300组进行训练,70组进行测试。在SLFRWNN模型中,需要对威胁数据进行归一化处理,范围在[0,1]之间。

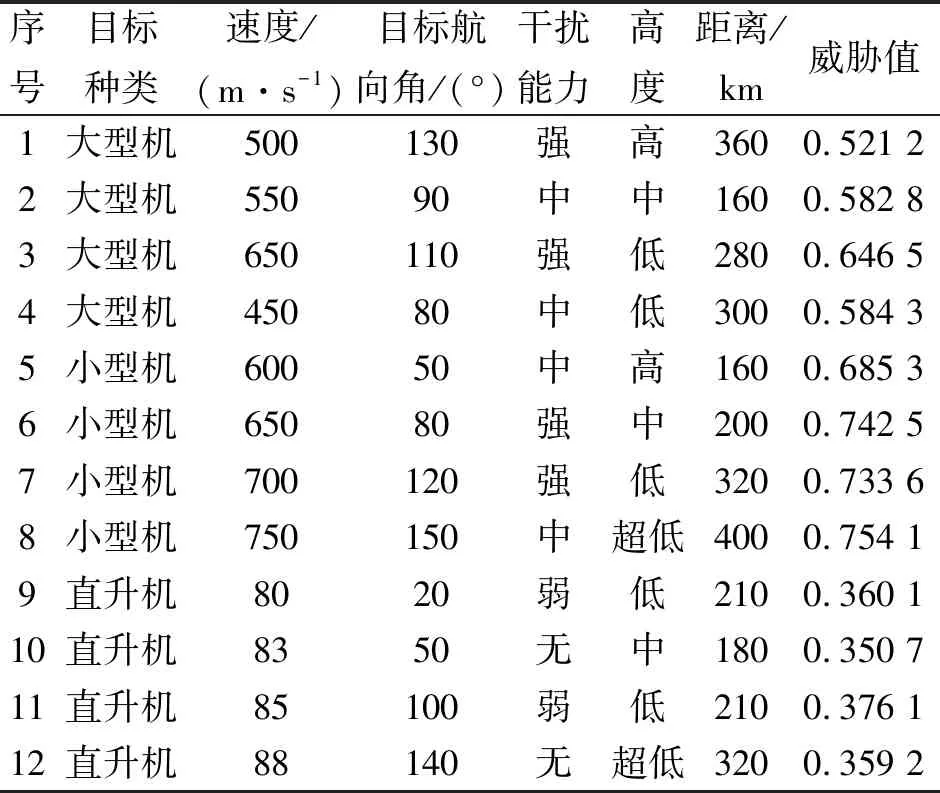
表1 部分目标威胁数据库数据

6 基于SLFRWNN的目标威胁评估仿真实验

SLFRWNN网络一共有6层。由于该模型输入、输出是六维和一维,因而对应每层神经元分别为6—6×5—5—6×5—5—1。第一层是上述6种典型指标的μ值,第二层隶属度函数层有6×5个节点,第三层模糊规则层有5个神经元,第四层递归小波变换层有6×5个节点,产生层为5个节点,第五层输出层为预测目标威胁值。根据大量实验数据计算,设置合适的网络参数,其中迭代次数设置为500,遗传算法的迭代次数、交叉概率、变异概率分别设置为30,0.2,0.1。经过遗传算法得到的参数如表2和表3所示。

表2 模糊规则前件部分参数

表3 模糊规则后件部分参数

本文分别采用GA-SLFRWNN、SLFRWNN和FNN 3种建模方法进行仿真,遗传算法适应度变化如图3所示,仿真实验对比如图4所示,对3种网络模型进行建模并对预测值与真实值进行对比分析,得到如图5所示的误差曲线和如图6所示的绝对误差百分比曲线。

图3 遗传算法适应度曲线 图4 预测输出结果对比图5 3种网络的绝对误差

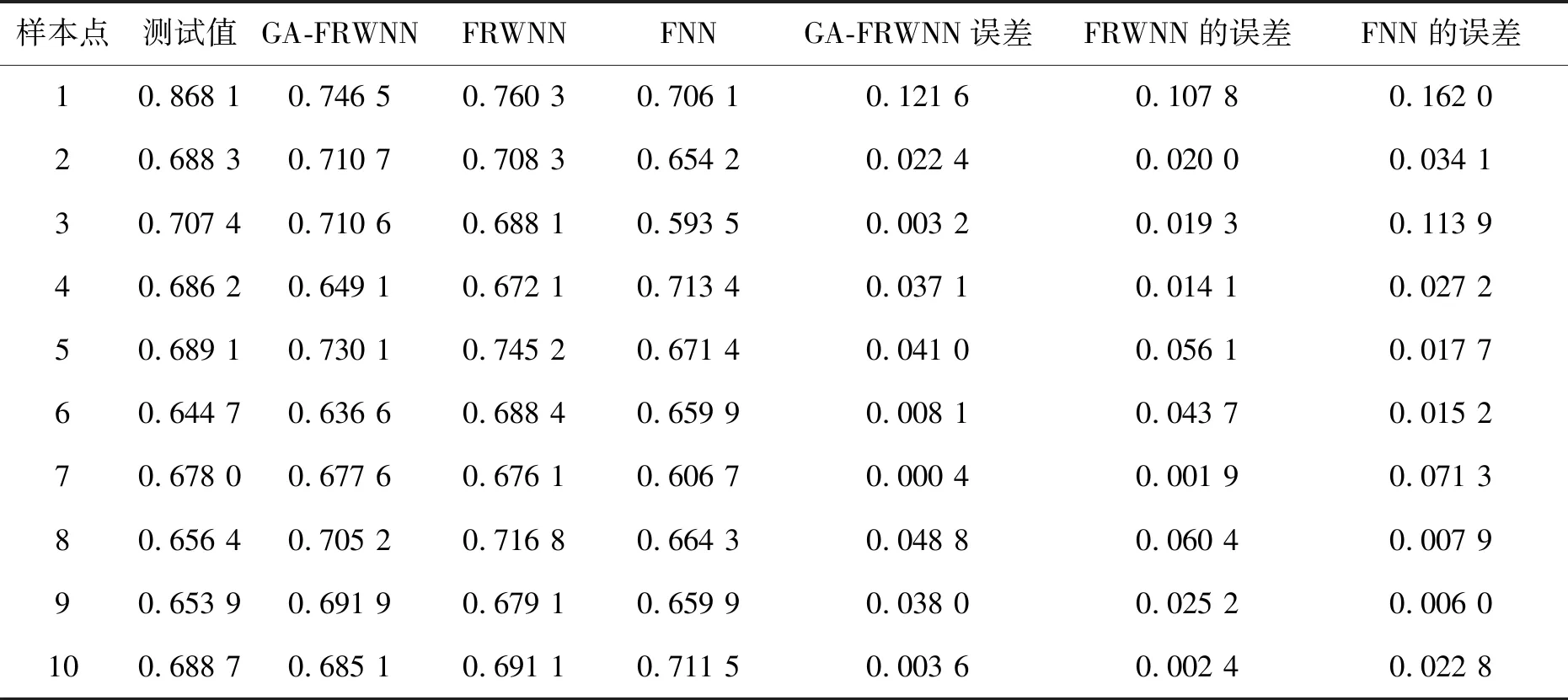
样本点测试值GA-FRWNNFRWNNFNNGA-FRWNN误差FRWNN的误差FNN的误差 10.868 10.746 50.760 30.706 10.121 60.107 80.162 0 20.688 30.710 70.708 30.654 20.022 40.020 00.034 1 30.707 40.710 60.688 10.593 50.003 20.019 30.113 9 40.686 20.649 10.672 10.713 40.037 10.014 10.027 2 50.689 10.730 10.745 20.671 40.041 00.056 10.017 7 60.644 70.636 60.688 40.659 90.008 10.043 70.015 2 70.678 00.677 60.676 10.606 70.000 40.001 90.071 3 80.656 40.705 20.716 80.664 30.048 80.060 40.007 9 90.653 90.691 90.679 10.659 90.038 00.025 20.006 0 100.688 70.685 10.691 10.711 50.003 60.002 40.022 8

图6 3种算法的绝对误差百分比

由图4可以清晰地看出,SLFRWNN模型预测值与实际威胁值的绝对误差比FNN的误差小,而通过GA优化的SLFRWNN模型预测的结果又优于SLFRWNN。由此可知,GA-SLFRWNN模型的预测结果非常理想,绝对误差值较小,而且性能稳定。由表4计算可得,基于遗传算法优化模糊递归小波神经网络预测的绝对误差和为0.324 2,模糊递归小波神经网络的绝对误差和为0.350 9,而模糊神经网络的绝对误差和为0.478 1。这说明模糊神经网络对数据的学习能力还是有所欠缺的。仿真结果表明:模糊递归小波神经网络对数据的学习能力强于传统的模糊神经网络,具有更好的收敛效率和精度,而经过遗传算法的优化可以使网络具有更好的学习能力,从而进一步验证了GA-SLFRWNN目标威胁评估模型的优越性和准确性。

7 结 论

针对空战中目标威胁评估不确定信息的问题,使用基于模糊递归小波神经网络对目标威胁评估进行建模,并采用GA对模型初始参数进行优化选取,通过Lyapunov稳定性理论得出了最优学习率。仿真实验表明:相比于FNN和FRWNN,该算法提高了系统的稳定性,加快了收敛速度,增强了预测精度,可以作为今后空中目标威胁评估的有效方法。