改进人工免疫算法的多机协同空战目标分配方法

高阳阳, 陈双艳, 余敏建, 海静, 房瑞跃

1．中国人民解放军93175 部队，吉林长春130000; 2．空军工程大学空管领航学院，陕西西安710051;3．中国人民解放军94754 部队，浙江嘉兴314000; 4．中国人民解放军95026 部队，广东佛山528000

近年来,随着高新技术的快速发展,战斗机协同空战已成为现代空战的主要作战样式。在多机协同空战中,如何根据战场态势,合理分配目标,充分发挥多机协同空战的整体作战效能,是多机协同空战指挥决策中最为关键的问题之一。目前,用于求解目标分配问题的方法有粒子群算法[1]、遗传算法[2]、蚁群算法[3]、萤火虫算法[4]及其混合优化算法[5]等。但这些算法收敛速度很慢,有时得不到稳定的解,严重影响指挥员进行空战决策。

人工免疫算法从提出至今已被广泛应用于各领域,如模式识别[6]、网络安全[7]、图像处理[8]等。文献[9]在采用自适应锦标赛选择算子的基础上,引入“(1+λ)-选择”全局更新技术对人工免疫算法进行改进,解决了武器-目标分配问题;文献[10]提出了一种新的编码方案和亲合度算法对免疫算法进行改进,解决了编队防空火力分配问题;文献[11]为防止人工免疫算法提前陷入局部最优,对抗体群进行改造,解决了火力分配问题。随着免疫算法越来越受到学者的关注,出现了一些与并行免疫算法有关的研究成果。文献[12]为求解大规模TSP问题,提出了一种基于TMSM的并行免疫记忆克隆选择算法;文献[13]为克服克隆选择算法收敛速度慢的缺陷,采用定向突变的自适应并行搜索策略对传统免疫算法进行了改进;文献[14]为克服传统遗传算法在求解路径规划问题时,不能以概率1进行收敛的缺陷,提出了一种基于抗体-抗原亲合度、抗体-抗体亲合力自适应动态调整的伪并行免疫算法。但以上算法存在如下问题:缺少种群间信息的交换,搜索效率低,容易出现早熟收敛现象。

基于此,本文在研究了传统和改进人工免疫算法的基础上,设计了一种并行人工免疫算法以提高算法搜索效率,并采用新的移民算子实现2个种群间的信息交换,从而保证种群的多样性。最后利用改进人工免疫算法求解多机协同空战问题,得到了最优分配方案。

1 多机协同空战目标分配数学模型

多机协同空战目标分配是指挥决策过程中一个十分重要的环节。本文以多机协同空战为背景,采用简明实用的非参量法对多机协同空战目标分配问题进行数学建模。传统的综合优势函数主要是根据角度优势、距离优势和能量优势进行构造,但随着战机性能在空战中发挥的作用越来越明显,传统的综合优势函数已经不适用于现代空战中的多机协同目标分配问题。因此本文以传统模型为基础,考虑战机性能优势,建立如下空战优势评价指标体系:

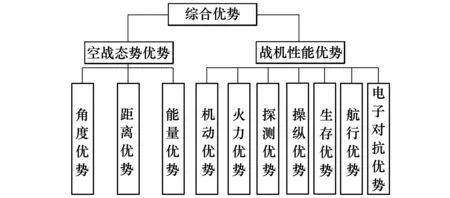
图1 空战优势评价指标体系

1.1 角度优势

(1)

式中,ψa为目标方位角,ψt为目标进入角。其中:ψa∈[0,180];ψt∈[0,180]。

1.2 距离优势

(2)

式中,rij为我方第i架战机与敌方第j架战机之间的距离,rimissle和riradar分别为我方第i架战机的导弹射程和雷达最大探测距离。

1.3 能量优势

(3)

式中,Eg为战机单位质量的能量,h为战机高度,v为战机速度,g为重力加速度。根据(3)式建立能量优势函数如下所示

(4)

式中,Egi为我方第i架战机单位质量的能量,Egj为敌方第j架战机单位质量的能量。

1.4 战机性能优势

H=h/max(h)

(5)

式中

h=

[lnB+ln∑A1+1+ln∑A2+1]ε1ε2ε3ε4,

B为机动参数,A1为火力参数,A2为探测能力参数,ε1为操纵效能参数,ε2为生存力参数,ε3为航程系数,ε4为电子对抗能力系数。根据(5)式建立战机性能优势函数如下所示

(6)

式中,Hi为我方第i架战机的空战指数,Hj为敌方第j架战机的空战指数。

1.5 综合优势函数

S=k1S1+k2S2+k3S3+k4S4

(7)

式中,k1,k2,k3,k4为指标权重。传统权重值的确定,常常是由人为给出,有很大的主观性和盲目性。为了更加合理地处理客观信息,本文采用文献[15]中改进的熵权法确定指标权重。

1.6 综合优势函数矩阵

假设在一次空战中,我方战机n架,敌方战机m架。根据(7)式可得我方第i架战机对敌方第j架战机的综合优势值Sij。从而可以建立起综合优势函数矩阵S。

S={Sij},i=1,2,3…,n;j=1,2,3…,m

(8)

多机协同空战目标分配目标函数定义为

(9)

式中,xij表示我方第i架战机是否分配给敌方第j架战机,xij=1表示是,xij=0表示否。

约束条件:

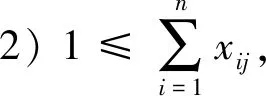
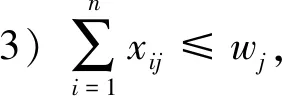
2 改进的人工免疫算法

2.1 初始种群的产生

传统的人工免疫算法采用单种群方式进行进化,容易产生早熟收敛现象。有些并行人工免疫算法采用多种群并行进化的方式,但是多采用比较单一的随机方式产生初始种群,通过移民算子进行多种群间的个体交换后,很难打破各种群内部的平衡,其保持种群多样性的效果不是十分明显。

本文设计的并行人工免疫算法采用2种不同的方式产生初始种群,分别为随机和人工方式。随机方式是在满足4个约束条件的前提下,随机产生的初始解,具有较强的随机性。人工方式是由人为确定的满足约束条件的初始解,具有较强的主观性。分别采用随机和人工方式产生的2个初始种群,使2个种群在产生之处就具有不同的特征,通过移民算子进行种群间个体交换后,能够打破2种群内部的平衡,增强种群多样性,使种群向着更高级别进行进化,从而得到全局最优解。

2.2 亲合度函数和编码方式的选择

人工免疫算法是模仿生物信息系统中的抗原识别、记忆等功能而提出的一种智能计算方法。多机协同空战目标分配问题与人工免疫系统(AIS)有很多相似之处,如表1所示。

表1 AIS与多机协同空战目标分配问题比较

由表1和2.1节可知,人工免疫算法的抗原为公式(9),抗体为满足公式(9)和约束条件1)～4)的解。抗体-抗原亲合度直接采用归一化后的目标函数进行评价

(10)

本文采用传统的整数编码方式,以我方战机数量为编码长度,即基因长度为n。抗体位上记录的编号为敌方战机代号,抗体位序号为我方战机代号。具体编码过程如图2所示。

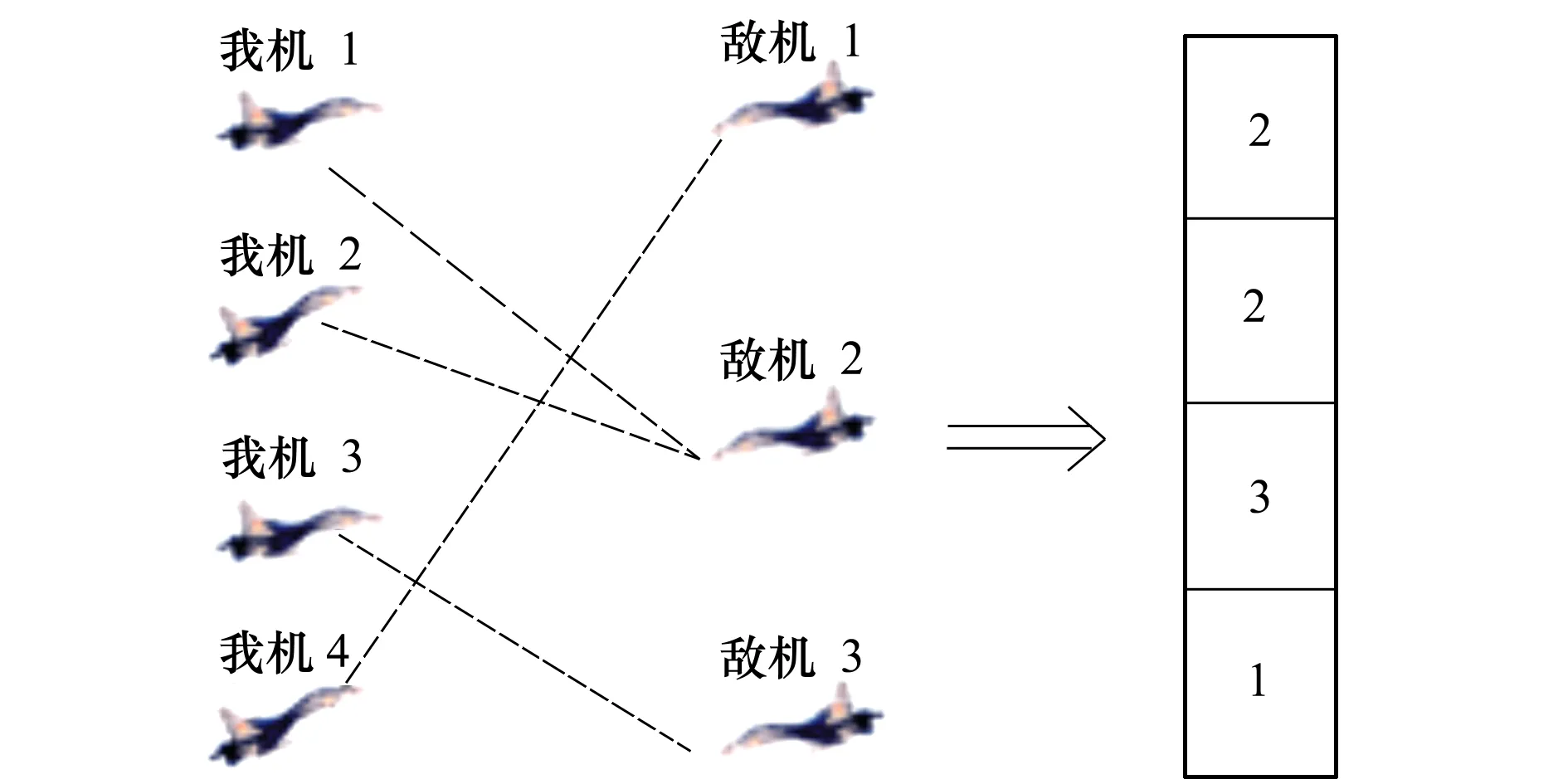
图2 抗体编码过程

2.3 交叉、变异算子

为了保持种群的多样性,防止过早收敛,通常要进行交叉、变异操作。通过选择算子保留下来的抗体按照一定的概率进行配对交叉,然后根据变异概率进行变异操作,从而得到新的抗体。

本文分别采用2种交叉、变异算子,具体变换如下所示:

交叉算子1

交叉前

2313………67

13556………21

交叉后

13313………67

22556………21

交叉算子2

交叉前

27125………46

25651………34

交叉后

65125………4625271………34

变异算子1

变异前

22315………14

变异后

43315………14

变异算子2

变异前

25421………63

变异后

25241………63

2.4 移民算子

移民算子的作用是为了实现2个种群间信息的交流,使种群向着更高级别进化,保持种群的多样性。本文在传统移民算子的基础上提出了一种新的移民算子。算法步骤如下所示:①确定2个初始种群,计算2个种群内每个个体亲合度。②将2个种群内的个体按照亲合度大小进行排序。③将2个种群内排序好的个体按照亲合度大小平均分成大、中、小3段。④设定种群间个体交换规模,本文取15%。⑤按照优者多选,劣者少选的原则,将2个种群内的每段按15%×(1,0.9,0.1),15%×(1,0.7,0.3),15%×(1,0.8,0.6)比例选择。⑥将选出的个体进行种群间交换重新产生2个新种群。

以比例(1,0.7,0.3)为例,将上述思想用图形表示。

图3 种群间个体交换示意图

2.5 并行人工免疫算法设计

传统人工免疫算法多采用单种群进化方式,缺少种群间信息之间的交流,搜索效率低,难以保持种群多样性,容易陷入局部最优。基于此,本文设计了一种并行人工免疫算法,具体操作流程和算法流程图如图4所示。

具体操作流程如下。

1) 分别采用随机和人工2种方式产生初始种群A、B。采用整数编码方式对种群中的个体进行编码,以(10)式作为亲合度函数。

2) 设置独立运行代数n,种群A、B分别采用不同的选择策略、交叉操作、变异操作进行进化。

3) 当种群A、B进化到指定代数时,采用新的移民算子进行两种群间个体交换。

4) 设置独立进化代数m,按照上图独立运行方式继续进行进化操作。

5) 判断是够满足终止条件。如果满足条件则输出结果,否则返回步骤3)。

6) 2条子线计算结束后,选择亲合度函数值大的结果作为问题的最优解。

图4 并行人工免疫算法流程图

3 仿真分析

3.1 算例仿真

在某次空战中我方战机7架与敌方5架遭遇。其中我方1架战机只能攻击敌方1架战机,敌方战机2,3,5可同时被我方2架战机攻击。g取9.8,k1=0.239 730,k2=0.304 524,k3=0.186 341,k4=0.269 405。根据战场某一时刻敌我双方的态势信息,由公式(1)～(7)求得我方战机对地方战机的综合优势值，如表2所示。

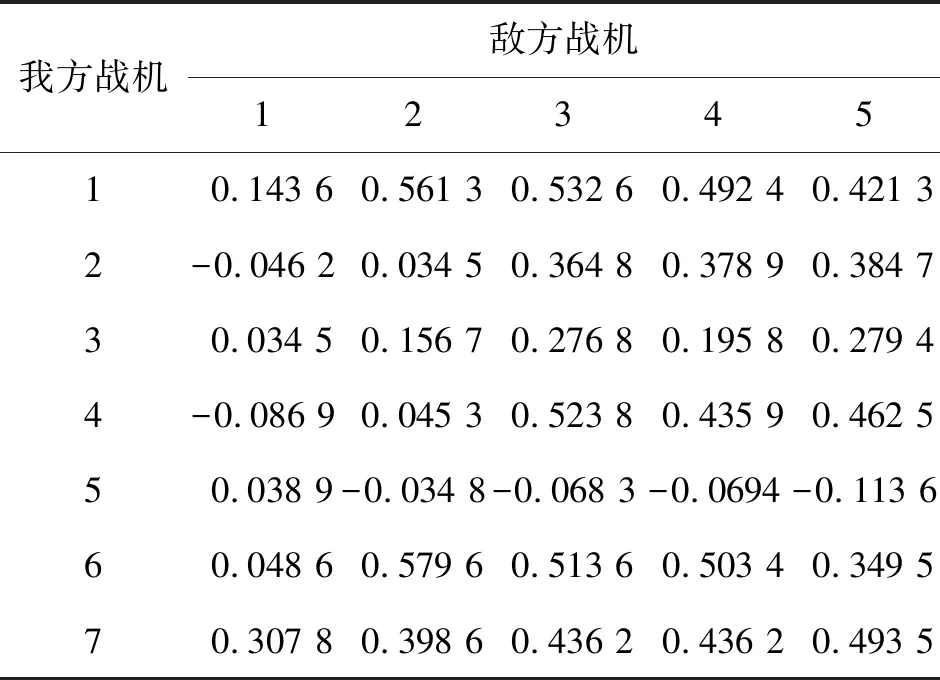
表2 我方对敌方战机综合优势表

2个初始种群大小取50,独立运行代数分别设定为10代、40代,选择、交叉、变异操作采用图4中方法,交叉概率取0.7,变异概率取0.05。针对3种迁徙比例A(15%,13.5%,1.5%),B(15%,12%,9%),C(15%,10.5%,4.5%)按照本文提出的改进人工免疫算法进行仿真。3种迁徙比例对应的最优亲合度演变过程如图5所示,最优目标分配方案如表3所示。

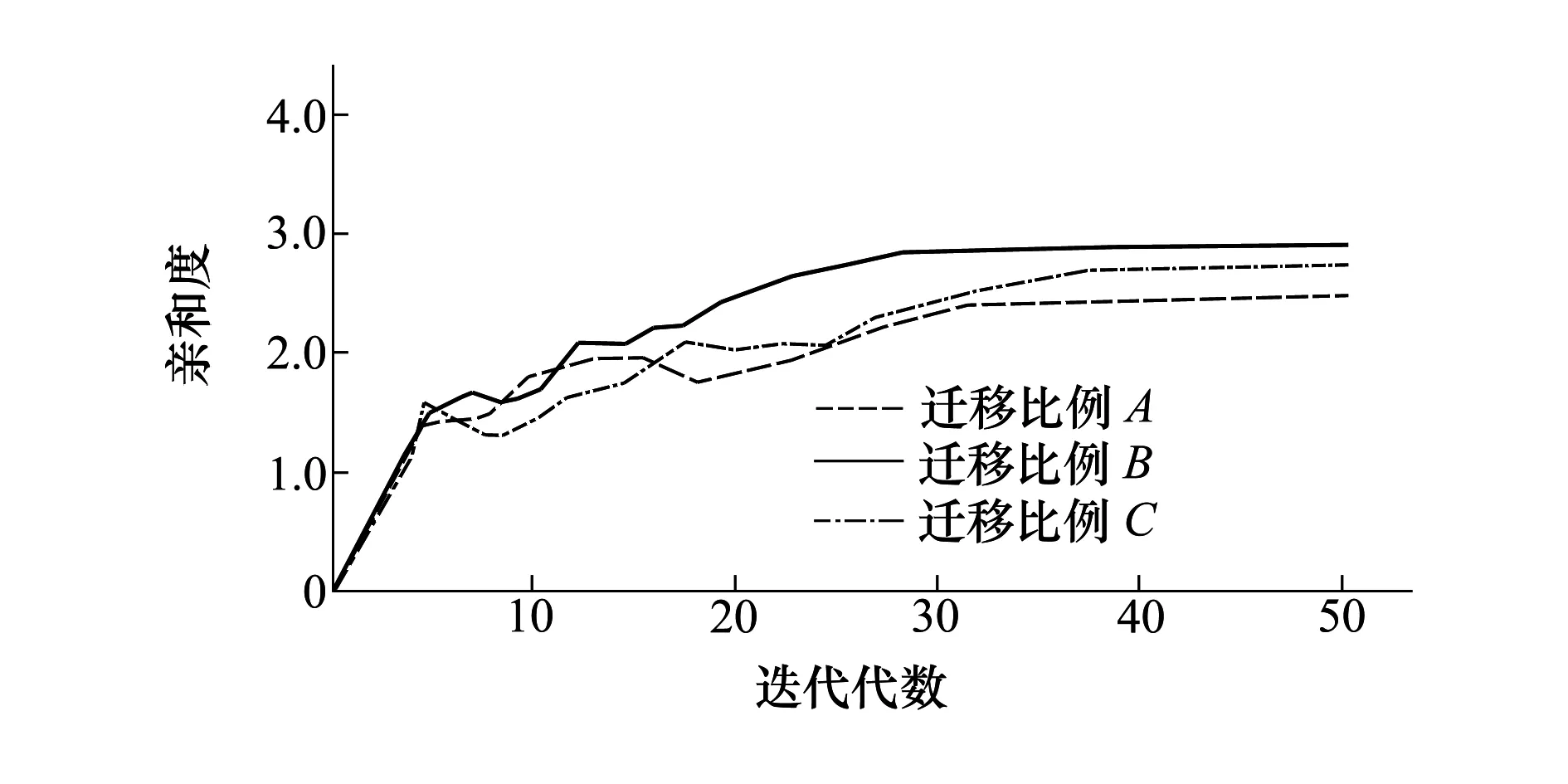
图5 3种迁徙比例最优亲合度演变

从图5可以看出,改进的免疫算法采用迁徙比例(15%,12%,9%)时,在最优值求解上要优于另外2种比例。

表3 最优目标分配方案

表3为采用迁徙比例为(15%,12%,9%)时,得出的最优分配方案。分配方案为我方战机5攻击敌方战机1;我方战机6攻击敌方战机2;我方战机1、4同时攻击敌方战机3;我方战机2攻击敌方战机4;我方战机3,7同时攻击敌方战机5。目标分配后,多机协同整体作战效能为2.826 7。

3.2 改进人工免疫算法性能分析

为了进一步分析本文所提算法性能,现将本文算法与传统人工免疫算法、文献[11]中的改进人工免疫算法和文献[14]中的并行免疫算法进行比较,本文所提算法分别采用迁徙比例A,B和C分别对文献[11]中的算例进行30次仿真。4种算法最优值求解和消耗时间统计结果如表4～表7所示。

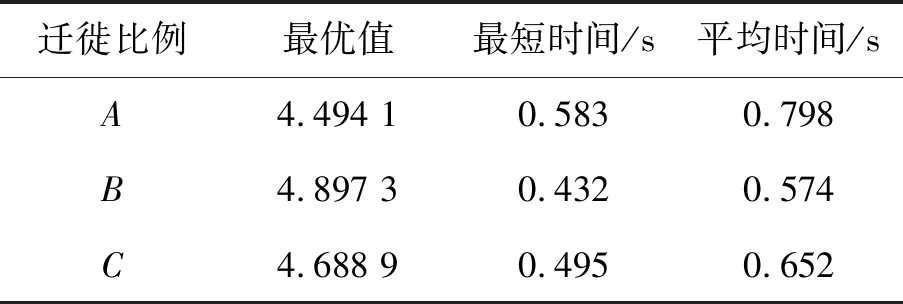
表4 本文算法最优值和消耗时间统计结果

表5 传统算法最优值和消耗时间统计结果

表6 文献[11]算法最优值和消耗时间统计结果

表7 文献[14]算法最优值和消耗时间统计结果

从表4可以看出,采用本文算法对文献[11]中的算例进行仿真,在采用迁徙比例B时,效果最好,采用迁徙比例C时,效果其次,采用迁徙比例A时,效果最差。将表4分别与表5、表6和表7进行对比可得:本文算法在采用迁徙比例B时,与其他3种算法相比具有比较明显的优势;本文算法在采用迁徙比例C时,较传统算法和文献[11]中算法有比较明显的优势,较文献[14]中算法,优势很小;本文算法在采用迁徙比例A时,与传统算法相比较,有明显的优势,与文献[11]中的算法相比较,优势很小,与文献[14]中的算法相比较,具有一定的劣势。进一步说明了本文中改进人工免疫算法的性能受迁徙比例的影响,在采用迁徙比例(15%,12%,9%)时,算法效果最优。采用并行运行方式并增加迁徙操作,能够实现2个不同种群间信息的交流,增强种群多样性,从而有效地改善最优策略的求解精度,提高算法收敛速度。

4 结 论

本文在分析了多机协同空战目标分配问题特点的基础上,提出了改进人工免疫算法的多机协同空战目标分配方法。建立了多机协同空战目标分配数学模型,设计了一种并行人工免疫算法,给出了改进人工免疫算法的具体流程,并针对3种迁徙比例进行了仿真分析,验证了改进人工免疫算法在采用迁徙比例B时,能够取得更优的结果。将改进人工免疫算法与3种人工免疫算法进行了比较,在大多数情况下,改进人工免疫算法与其他3种人工免疫算法相比,能够在更短的时间内求得更优的结果。