基于改进K-means聚类算法的金鱼阴影去除及图像分割方法
王 帅,刘世晶,唐 荣,陈 军,刘兴国
(中国水产科学研究院渔业机械仪器研究所,上海 200092)
运动鱼类检测是鱼类行为量化研究中的关键技术和难题[1]。受光照条件和自身运动影响,鱼类运动会产生随机阴影噪声,增加了图像分割难度。复杂背景的目标对象提取是目前运动检测研究的热点,目前尚未看到有关鱼类图像运动阴影去除方面的研究报道,但在运动人群及运动车辆检测方面已经开展大量的工作,梳理近年来的研究成果,相关研究主要聚焦在基于颜色特征分割方法和基于纹理特征分割方法两大类。基于颜色的方法主要是通过阴影的色度不变性分割目标对象。Cucchiara等[2]在HSV颜色空间中使用色度、饱和度及亮度信息建立背景模型,分离样本图像的亮度及色度分量,确定阴影范围;徐少飞等[3]发现一种基于颜色属性的运动阴影消除算法;Sun等[4]利用C1C2C3色彩空间的光照不变性和HIS色彩空间中图像的色度和亮度比值,实现阴影分割,但由于没有考虑前景和背景差异度,增加了背景识别误差。基于纹理信息的方法是利用阴影的纹理相似性实现背景识别。Leone等[5]发现一种利用Gabor函数进行样本图像的纹理特征提取,从而检测出阴影区域并去除;郭春凤等[6]提出一种融合D1D2D3模型和LBP纹理特征的LPTD算子,实现运动目标背景检测;曹健等[7]提出一种将区域颜色融合图像LBP纹理进行不同环境下的运动阴影区域检测。以上基于纹理信息的方法,虽然可以获得一些效果,然而当样本图像存在平坦区域或者目标与背景纹理特征接近时,会产生较多误分割现象。
聚类算法是利用不同类型特征之间的特征距离分割目标对象,可融合多种不同特征,是一种常用的数据分类方法。目前常用的图像分割聚类算法有K-means算法及FCM(Fuzzy c-means)算法,Rocha等[8]在HSV色彩空间通过利用K-means算法提取图像样本的背景,进而去除阴影;巨志勇等[9]将K-means算法与分水岭算法相结合进行果蔬图像分割;龚劬等[10]提出一种基于图论的FCM图像分割算法。相比于基于颜色特征和纹理特征的分割算法,聚类算法在背景分割方面具有较好的分割效果。但是,由于典型聚类算法对聚类中心和噪声点较为敏感,易于陷入局部极小解,导致算法适应性较差,尚不能满足水下对象的背景分割要求。本研究以金鱼为目标对象,提出一种改进的K-means背景去除方法。该方法采用马氏距离作为距离度量算子,可优化聚类个数以及初始聚类中心点选择方法。
1 材料与方法
1.1 金鱼图像
试验用鱼为草金鱼,购于上海市曲阳花鸟市场,金鱼平均体长约为10 cm。试验开展前,先将鱼放于养殖鱼缸暂养数月,使其充分适应试验环境。试验设备主要有小蚁微单相机(CCD:Sony IMX269 M4/3,分辨率5 184 × 3 888 pixels,焦距12~ 40 mm)、玻璃鱼缸(100 cm×75 cm×40 cm)和相机固定支架等(图1)。

图1 试验设备Fig.1 Experimental equipment
试验过程:1)相机放置于玻璃鱼缸中心正上方位置,垂直距离110 cm;2)为保证成像质量,相机镜头与玻璃鱼缸的水平面近似于垂直;3)在室内正常的光照强度条件下采集图像,相机焦距和光圈设置到正好可以完全拍摄玻璃鱼缸,设置自动白平衡;4)采用等比例方法压缩图像,综合考虑图像大小和分辨率,采用10倍压缩比例,压缩后图像分辨率为518×388(图2)。从图2中可以看出,光线照射到运动的金鱼身上产生了明显的阴影区域,且阴影区域映射了金鱼的体色。在室内开放条件下,由于拍摄的时间不同,会有不同方向的入射光,因此会造成金鱼样本图像产生不同形状及不同大小的阴影区域,增加阴影去除的难度。

图2 金鱼图像Fig.2 Goldfish image
1.2 研究方法
1.2.1 颜色空间转换
寻找恰当的颜色空间是有效进行图像分割的第一步,而且对使用的方法及策略至关重要[11]。目前比较常用的是RGB 颜色空间,可以用R、G、B三基色的组合来表示全部的颜色,这3个分量拥有极强的相关性,所以并不适应于直接用来基于三分量独立运算的图像分割[12-13],可以使用RGB 颜色空间通过各种不同的变换得到其他颜色空间。Lab颜色空间是一种颜色度量的国际标准[14-15],是一种与设备无关的色彩模型[16-17],可以运行于全部的图像相关设备上,能够确保图像相关设备输出图像转换后的颜色拥有一致性[18],因此Lab颜色空间可以克服RGB等其他颜色空间对图像设备色彩特性的依赖性。Lab颜色空间分开保存一幅图像的色彩及亮度信息,其由L、a和b三个分量(通道)组成,并分别作为Lab颜色空间的三个坐标轴[19]。其中,L描述亮度,从纯黑到纯白,其对应值域为[0,100];a描述从绿色(-)到红色(+);b描述从蓝色(-)到黄色(+);a和b对应的值域为[-128,127]。Lab颜色空间可以由RGB 颜色空间通过创建一个由X、Y和Z三个原色组成的色彩空间非线性转换得到[16]。
1.2.2 改进K-means算法
目前K-means算法被广泛用于模式识别、机器学习和数据挖掘等方面[20]。通常情况下K-means算法拥有简易、效率高、容易理解、高性能及可拓展性好等优势,然而对于一些数据,该算法又有无法准确确定初始聚类中心数目及其初始数值对聚类结果影响极大、一般具有圆形或者球形簇的聚类结果及其仅在定义簇的均值时才可以被使用、对于孤立的数据点或噪点比较敏感、易于陷入局部极小解等劣势。为了解决以上问题,本研究提出了一种改进的K-means算法,分别从去除噪点及孤立数据点、使用马氏距离作为距离度量方法、明确聚类个数以及初始聚类中心点选择等领域进行优化。
(1)中值滤波。由于拍摄环境条件的变化、光照及其电磁波等外界因素的影响,会造成拍摄图像产生噪点及孤立的数据点,对于后续图像的分割处理会带来很大的干扰[21]。为了获得好的分割结果,同时解决传统算法对噪声点及孤立数据点比较敏感这一问题,本研究使用中值滤波[21]对样本图像进行预处理,尽可能去除噪声点及孤立点造成的影响。
(2)马氏距离。K-means算法一般采用欧式距离作为其距离相似度度量方法,然而欧式距离不区分样本不同属性间的差异,同时未能包含样本总体变化和差异对距离大小带来的影响,这往往不能符合实际使用要求。因此,本研究提出使用马氏距离来代替欧式距离衡量样本之间的相关性。马氏距离是一种使用样本间的方差与协方差来描述样本集合的分布情况,不会受到样本量纲和测量尺度的干扰,同时还能去除样本变量间的相关性影响[22-23]。马氏距离的数学解释为:令样本集P={x1,x2,…,xn},其中n为样本的个数。此时样本xi,xj之间的马氏距离dij为:
(3)群G为素数幂阶循环群.设有限群G的阶为,由(1)和(2)知G为循环群.若s≥2,则生成元个数1)···(ps-1)≥2,故可选取两个不同生成元x,y,再取p1阶元a,p2阶元b以及单位元1构成子集N={1,a,b,x,y},此时的诱导子图P(N)如图2所示,由引理1知P(G)不是某图的线图.
(1)
式中:dij是样本i到样本j的马氏距离;xi是第i个样本的属性向量;xj是第j个样本的属性向量;T是矩阵转置符号;m是待测样本的协方差矩阵。dij对于所有的i,j及k值应该符合4个条件:只有在i=j时,dij=0;dij>0;dij=dji;dij≤dik+dkj。
(3)确定聚类个数K。选取DBI指标(Davies-Bouldin)[24]评价K值的选取是否最佳。DBI指数是一个使用类簇内数据的紧密情况来评价聚类算法聚类效果好坏的度量指标,是计算类内的距离之和与类间的距离之和的比值,本质上属于内部评估。DBI值的计算步骤为[24]:
第一步,假设待测样本中描述第i类内的数据集合分散程度的分散度值为S,且其可由公式(2)得到:
(2)
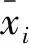
第二步,令第i类的质心与第j类的质心间的欧几里得距离为D,其表达式为:
(3)
第三步,令i和j类间的相似度值为R,利用分散度和欧几里得距离的相互关系可以得到:
(4)
最后一步,DBI的值即是全部分类(各个分类和其它分类之间)的最大相似度的平均值,可由下式得到:
(5)
(4)初始聚类中心点选择。首先将样本数据集合中密度最大的数据点选择为首个初始聚类中心点,并且使用该基本准则寻找距离第一个聚类中心最大的点作为第二个初始聚类中心点,然后将离的最近的数据点全部分配到同一类簇。这样选取初始聚类中心点可以解决传统K-means算法有可能存在选择事实上是同一分类内的点作为初始聚类中心点的问题,同时可解决该算法有可能存在某个类簇将样本数据集合中密度过高的点错误分配到自己类别的问题[25]。初始聚类中心点具体选择步骤为:设定一个阈值计算出样本集各个数据点的密度,找出其中密度最大的一个数据点并设为第一个初始聚类中心点k1,然后计算其他数据点到k1的马氏距离,找到其中距离最大的点即第二个初始聚类中心点,如此循环,找到K个初始聚类中心点结束。
2 结果与分析
2.1 颜色空间转换分析
使用合适的颜色空间对于分割彩色样本图像来说至关重要。因为当同一张彩色样本图像使用不同的颜色空间进行预处理时,不同颜色分量的灰度图像会相差很大,所以应该选择可以很容易区分金鱼目标和背景的颜色分量。将金鱼样本图像从RGB 颜色空间转换到Lab 颜色空间,L、a及b分量图像及对应的直方图(图3)。因为L表示图像的亮度,和人眼的感知相关,而且从图3d的L分量直方图能够得到,L分量中金鱼的亮度较大,然而相对于背景颜色来说没有显著的差别,因此可以不考虑L分量。从图3e、图3f的a和b分量的直方图可以看出金鱼和背景的颜色基本一致,金鱼与背景呈现出显著的双峰,因此,提取Lab颜色空间的a、b分量分割金鱼与背景。

图3 金鱼图像Lab各分量及其直方图Fig.3 Each component of goldfish Lab image and its histogram
2.2 不同聚类算法分析
首先使用中值滤波算法去除采集金鱼图像的噪点,结果如图4a所示。再将去除噪点后的彩色图像从RGB颜色空间转化到Lab颜色空间,结果如图4b所示,然后使用改进的K-means算法对其进行聚类,其中距离相似度度量参数选择马氏距离,聚类结果如图4c所示。

图4 金鱼运动阴影去除及图像分割实验流程图Fig.4 Experimental flow chart of goldfish motion shadow removal and image segmentation
为了验证算法的有效性,选择含有多条样本的金鱼图像,分别使用传统K-means算法和FCM算法进行阴影去除及图像分割实验,结果如图5所示。

图5 3种不同算法阴影去除及图像分割结果图Fig.5 Shadow removal and image segmentation results using three different algorithms
与上述两种算法相比,本文算法在去除阴影方面取得了更好的效果,目标对象分割丢失特征较少,4条金鱼的轮廓完整,纹理清楚,但是尾部出现部分丢失;使用传统K-means算法和FCM算法得到的金鱼虽然轮廓完整,但受阴影干扰,有一部分阴影并未完全去除,总体的分割效果并不好。
为了验证本文算法的有效性,引入误差概率来对比三种算法的优劣。从图像分割结果来看,分割率低将会造成像素的错分,因此,被错分的像素数量可以作为一种评价图像分割质量的数据标准。此时,误差概率能够由公式(6)计算得到:
PE=P(O)×P(B|O)+P(B)×P(O|B)
(6)
式中:P(O)为待处理图像中的目标所占比例的先验概率;P(B)为待处理图像中的背景所占比例的先验概率;P(B|O)为把检测目标误判为背景的概率;P(O|B)为把背景误判为检测目标的概率。
针对采集到的具有不同阴影区域的200张金鱼样本图像,使用误差概率和运行时间分别对基于改进K-means算法、传统K-means算法及FCM算法进行对比分析,3种算法的平均误分类概率及运行时间见表2。

表2 3种算法图像分割效果比较Tab.2 Image segmentation effect comparison of three algorithms
从表2可以看出,改进K-means算法的平均误分类的像素比率和平均运行时间分别为2.48%和0.875 s,均好于后两种算法。其中,传统K-means聚类算法因为无法准确确定聚类种类的数目,以及其值的敏感性、对噪声点及孤立数据比较敏感、随机选取聚类中心等缺点,致使其阴影去除及分割的效果不是很理想;FCM算法仅简单地从图像的像素灰度值考虑,只是依赖像素的分布强度,并未去除异常的数据,且忽略了可用的空间位置信息,导致FCM算法对噪声点极其敏感,因此其分割效果并未达到理想范围。
3 讨论
针对鱼类行为研究,有效对图像进行预处理,提取准确的前景信息,是开展鱼类行为分析的前提。采用视觉技术测量鱼类三维运动,仍需对单个相机拍摄图像进行预处理。因此,本研究从单个相机图像处理技术入手,采用单目相机拍摄鱼类运动图片,研究背景分割技术,适用于鱼类较少发生上下重叠的平面二维运动跟踪场景,可直接应用到三维运动图像预处理中。提出的阴影去除及目标分割方法能够较好地分割鱼类和背景,但当目标存在水平粘连时,仅仅依靠聚类算法不能满足个体分割或者运动跟踪前处理的图像分割要求,下一步研究将结合轮廓识别和运动方向预估辅助定位目标鱼类,以期提高图像分割效果。
复杂工况鱼类背景去除,不可避免地会受到相似背景干扰,针对鱼类目标个体,主要干扰因素包括相似背景、鱼类体色环境适应性以及光照条件。本试验采用聚类算法去除阴影,聚类目标为颜色空间,可充分利用背景和体色之间的颜色差异,适用于目标对象体色与阴影差异较大的试验场景。此外,由于Lab颜色空间中的L分量能够反应光照变化,聚类时采用a、b分量而忽略L分量可有效降低光照变化的影响,因此,基于Lab颜色空间的聚类分割算法对彩色图像和光照条件鲁棒性较好。针对体色较暗或者具备颜色适应性的目标对象,下一步工作将结合对比度增强及轮廓预识别功能初步定位目标鱼类,然后引入图像形态学处理技术开展精准分割研究。
算法运行时间是影响鱼类运动分析效能的关键因素,本文提出的基于聚类的背景去除方法,作为图像预处理算法,主要应用在行为分析的前处理过程,原则上要求具备较快的处理速度。本文通过压缩图像、降低图像分辨率提高算法运算速度,单帧图像的处理时间接近1 s,能够满足离线鱼类运动量化分析的需要,但图像处理时间还是较长。所以,本研究下一步将引入底层编码机制优化本文算法,进一步提高算法运行效率。
4 结论
以金鱼作为研究对象,提出了一种基于改进的K-means聚类算法的金鱼图像阴影去除及图像分割方法,效果较好。1)使用该方法对采集的200张具有不同阴影区域的金鱼样本图像进行分割试验,平均误分类的像素比率和平均运行时间分别为2.48%和0.875 s,可以较好地去除金鱼图像的阴影部分,好于使用传统K-means聚类算法和FCM聚类算法的分割结果。2)采用Lab颜色空间表述图像,可有效降低光照条件对图像的影响,有利于解决不同背景下的阴影去除及图像分割,提高算法的普适性。3)受算法本身运行逻辑的限制,算法运行速度较慢,因此,如何提高算法的运行速度将是下一步研究的重点方向。
□

