一种基于小波相关滤波的无线电干涉测量处理方法

路伟涛，任天鹏，陈略，韩松涛，王美

（1.北京航天飞行控制中心，北京 100094；2.航天飞行动力学技术国家级重点实验室，北京 100094）

引 言

无线电干涉测量技术具有测量精度高、作用距离远等优点，在深空探测任务中得到了广泛的应用[1-2]。但是航天测控信号特别是深空探测信号的发射功率有限，传播路径较长，测站接收的信号比较微弱，同时信道环境多变、测控设备复杂，限制了VLBI的测量精度[3-4]。通过增大基线长度、处理带宽以及接收天线口径、改善低噪放大器等途径可以在一定程度上提高系统的测量性能[5]，但代价较高。如接收天线口径增加一倍，接收信号信噪比约提高3 dB，但耗费增加却不止一倍；基线长度的增大受限于地球尺度[6]。

随着计算机技术的发展和信号处理算法的研究，从数据处理层面改善航天测控系统性能，是一种费效比相对可观的改进方案[7]，其中信号滤波是一种改善信号质量常用的处理手段[8]。小波变换以其多分辨率和紧至性在信号滤波处理中得到了广泛研究和应用[9-10]，现有小波滤波方法可大致分为3类：小波阈值滤波[11]、模极大值滤波[12]和小波相关滤波。考虑到航天测控信号和上述3类滤波算法的特点，小波相关滤波算法更适合处理航天测控信号。小波相关滤波最早由Within提出[13]，Xu等人提出了一种基于空域相关性的噪声去除方法（Spatially Selective Noise Filtration，SSNF）[14]，其基本原理就是利用信号与噪声的小波系数在相邻尺度间的相关性不同进行滤波。在该算法中噪声功率的估计关系到各尺度上阈值的设定，Pan等人给出了噪声功率阈值的理论计算公式，并给出了一种估计信号噪声方差的有效方法，使得小波相关滤波算法具有自适应性[15]。小波相关滤波存在以下两个问题。

1）小波系数在各尺度间的微小偏移降低了尺度间相关性和滤波性能。针对该问题，区域相关算法[16]、重复相关算法[13]、降低分解层数[17]等措施相继被提出和研究，但效果并不理想。

2）小波系数处理从低尺度向高尺度进行限制了滤波效果[18]。文献[19]利用尺度间归一化相关系数进行重构，增强了信号，抑制了噪声，但滤波性能改善有限；文献[19]将小波阈值滤波与小波尺度滤波结合，算法比较复杂；文献[17]提出了由高层向低层的逆序处理思路，但在具体算法中未能体现。

针对小波相关滤波的上述两个问题，文献[20]提出了一种基于移位相关的小波相关滤波算法，取得了较好的宽带信号滤波效果。本文首先简要论述了小波相关滤波算法原理，然后对航天测控宽带信号进行建模，在分析无线电干涉测量原理的基础上，提出了基于小波滤波的无线电干涉测量方案，最后利用实测数据进行了验证。

1 基于移位相关的小波相关滤波算法

1.1 小波相关滤波算法

相邻尺度间小波系数相关值定义

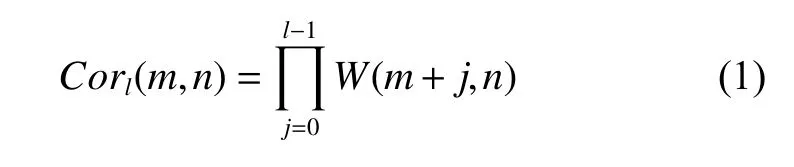
其中：m、l、n分别为待求相关系数尺度、尺度数目及小波系数的个数，W（m，n）为尺度m上的第n个小波系数，一般取l=2，记为Cor2(m,n)。需要对相关系数进行能量归一化

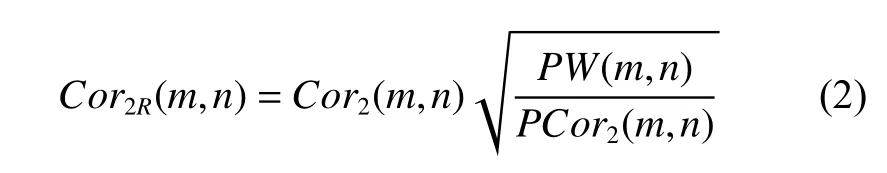
小波相关滤波算法步骤如下：

1）初始化分解层数m=Lev，滤波后的小波系数WF（m，n）为零，对信号进行平稳小波变换；

2）按照式（1）和式（2）求得m层小波系数的归一化相关值；

3）对m层所有小波系数W（m，n），n=1，···，N进行判断筛选。若则认为该点的小波系数由信号引发，该系数被保留至WF（m，n），并置零W（m，n）；反之，则认为该点由噪声产生。

4）重复步骤2）和3）直到W（m，n）的功率小于设定的阈值。

5）对所有分解层数进行步骤2）～4）的处理，得到滤波后的小波系数WF（m，n），进行逆小波变换得到滤波后的信号。

算法的关键在于第2）步中相关值的求解和第4）步中阈值的设定，其中阈值的设定可参考文献[17,21]，相关值的求解受到小波系数在各分解层间偏移的影响，下面对该问题进行解决。

1.2 小波相关滤波改进算法

1）移位相关处理

小波系数在各尺度间存在微小偏移，对小波系数尺度间的相关性产生影响，进而影响小波系数的筛选，最终影响滤波性能。分解层数越高，该偏移就越大；这种偏移与小波函数也有关系。

考虑到消失矩阶数和支撑长度在滤波算法中的影响[20]，选择db1小波进行小波分解，并通过理论推导给出了各层小波系数偏移量与分解层数的关系，以此解决偏移对相关系数带来的影响。

假设信号s(k)，k=1，···，N为由±1组成的序列，假设在k=k0,p处存在极性转换，即在k=k0,p附近的邻域[k0,p−L,k0,p+L],L∈N内存在如下关系

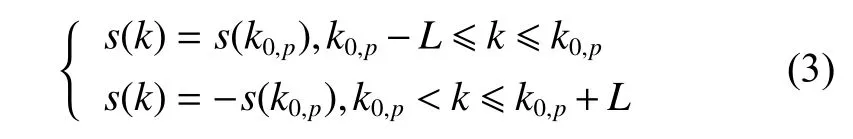
设s(k)第j层细节系数的某一峰值点位于kj,peak，第j+1层细节系数与此相对应的峰值点位于kj+1,peak，则满足

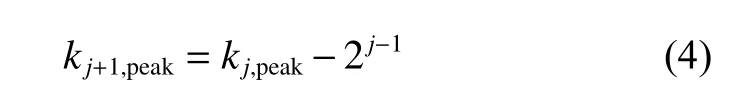
详细证明参见文献[22]。

2）低尺度小波系数处理

考虑到信号的小波系数在小波分解过程中逐渐增强，而噪声的小波系数则迅速减弱，那么可以认为在高分解层信号小波系数占绝对优势，高分解层间的相关结果中信号也占绝对优势，即随着分解层数的增加信号相关性增强。所以相关尺度滤波应从高尺度向低尺度逆向处理。

考虑到信号小波系数扩散现象[21]，当进行相关处理时，高分解层中被认为噪声的位置，在低分解层也必然为噪声。由此可以由高尺度处理结果向低尺度提供约束。另外，在提供约束时必须考虑小波系数在各层间的偏移量，避免将低尺度小波系数错误置零。

（1）遍历m（m=Lev，···，2）层小波系数，得到等于零的位置indexIsZero和不等于零的位置indexIsNonZero；

（2）利用前文小波系数在各层间的偏移量和indexIsNonZero，修正indexIsZero，得到index’IsZero；

（3）置零m–1层index’IsZero位置的小波系数。

低尺度小波系数处理通过两个方面进行改进：由高层向低层逆向处理，并由高层处理结果向低层处理结果提供约束。

3）高尺度小波系数阈值处理

由于高斯噪声经过小波变换后仍为高斯噪声，同样满足统计规律中的3σ准则。随着分解层数的增加，在高尺度小波系数中，信号占主导作用，噪声被大幅度抑制，所以这里选择硬阈值法进行处理

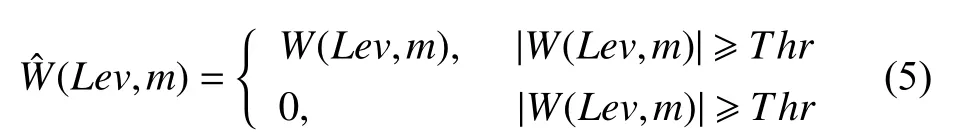
其中：Lev为小波分解的最高层数；Thr=c·σ为阈值；c为常数，为了避免错误置零小波系数，这里选择c=2.5；σ为Lev层小波系数的标准差。至此，可以给出改进的小波相关滤波算法：

（1）按照传统小波相关滤波算法进行处理，得到滤波后的小波系数WF（m，n），其中尺度间相关系数通过移位相关算法计算；

（2）对最高层小波系数WF（Lev，n）进行阈值处理，并更新WF（Lev，n）中的最高层小波系数，记为W’F（m，n）；

（3）从W’F（m，n）的高尺度系数向低尺度系数提供约束，继续处理Lev–1层，直至处理所有分解层。

2 基于小波相关滤波的无线电测量方案

2.1 宽带航天测控信号模型

无线电干涉测量只需接收航天器的下行信号，对信号类型没有明确要求。目前干涉测量试验中可接收航天器下行信号类型主要包括扩频信号、数传信号、遥测信号等。上述信号可统一由式（6）建模

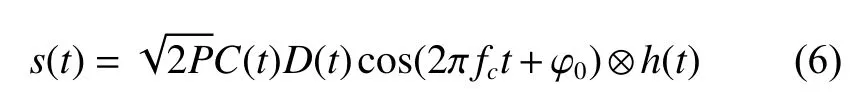
其中：fc为信号载波频率；C（t）是直接序列扩频码（若非扩频信号，则取值为1）；D（t）是宽带数传信号或遥测信号等；P是信号功率；φ0是载波信号初相；h（t）为带限滤波器；⊗表示卷积。

2.2 基于小波相关滤波的群时延估计方法

无线电干涉测量中，宽带信号的群时延估计一般采用FX型相关处理实现。其一般处理流程是在一定时延预测模型的基础上，在数据读取过程中进行整数比特延迟的补偿，然后做条纹反转降低条纹率，接着在频域做小数比特补偿，最后求取互功率谱，通过对功率谱相位拟合得到时延和条纹率的估计值[22]，处理流程如图1所示。

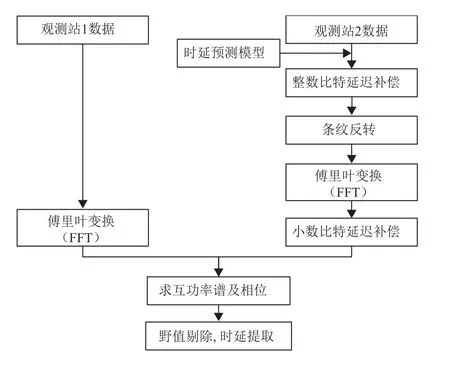
图1 FX宽带相关处理流程图Fig.1 The FX correlation scheme of wide band signal

设经过上述处理过程后两测站接收数据的频域表达为F1(ω)、F2(ω)，最后可得两测站信号互谱

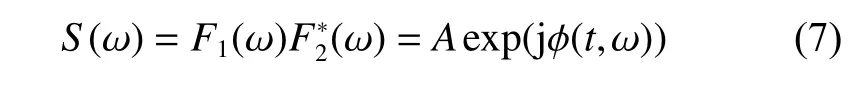
其中：A=|F(ω)|2；ϕ(t,ω)为互谱的相位。那么可得剩余时延∆τg

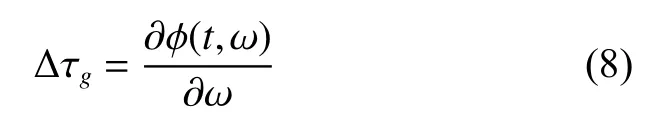
由式（8）可以知道，通过相位对频率的拟合即可得到剩余时延。考虑到噪声的存在，公式（7）改写为

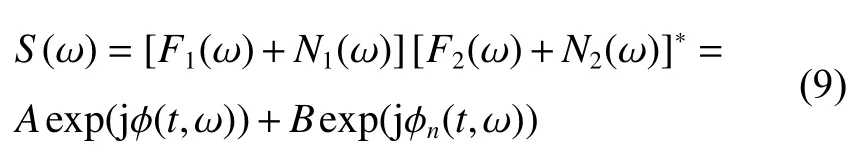
其中：Bexp(jϕn(t,ω))是3项含有噪声的频谱表达式。高斯噪声的频谱具有随机性，其相位也是随机的[23]，必然给式（8）中残余时延的求解带来误差。基于此，提出了基于小波相关滤波的群时延估计方案，如图2所示。两个测站接收的宽带信号首先进行小波滤波，再进行FX宽带相关处理，最后进行群时延估计。

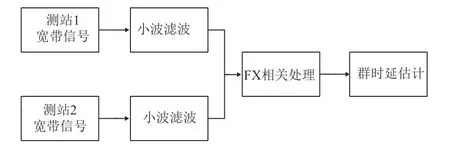
图2 基于小波相关滤波的群时延估计方案Fig.2 The group delay estimation scheme based on wavelet correlation filter

3 试验验证与分析

3.1 仿真分析

假设采样频率为56 MHz，扩频信号码速率为1.023 MHz，信号带宽为2倍码速率；信号数据长度为4 096。图3给出了信号在信噪比为10dB时含噪信号、滤波信号的时域波形对比（分解层数为4）。其中，“理想”表示为理想无噪声信号，作为滤波效果对比；“含噪”表示理想信号叠加噪声后的信号，为滤波处理的输入信号；“SSNF”表示传统小波空间滤波算法；“mySSNF”表示本文提出的改善小波空间滤波算法；下同。可以看出，经过滤波处理后，信号噪声均被明显抑制；相对传统滤波算法，改进算法滤波信号的残留“毛刺”相对较少，说明滤波性能更好。

以信噪比改善SNRimp和相对误差Rms为指标，如式（10）所示，考察传统相关滤波和改进算法的滤波性能。

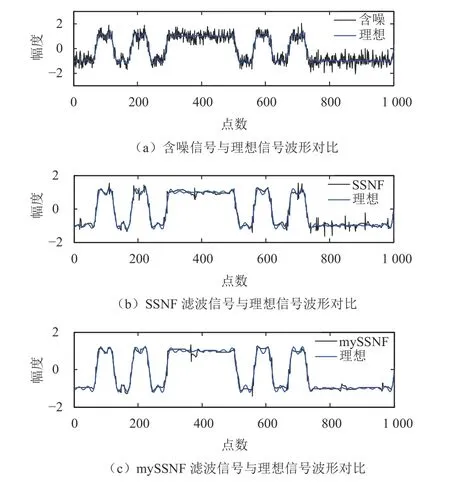
图3 传统相关滤波与改进相关滤波后时域波形对比（SNR=10 dB）Fig.3 The time domain comparison after processing by SSNF and mySSNF（SNR=10 dB）

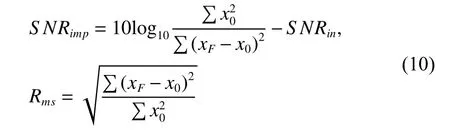
图4给出了不同噪声情况下，传统相关滤波和改进算法对带限扩频信号质量的改善情况（500次蒙特卡罗仿真）。由图4可以看出，经滤波处理后信号质量有所改善，低信噪比改善幅度大于高信噪比情况；改进算法滤波处理后信号质量改善幅度较传统算法稍高，信噪比改善幅度在低信噪比时约高2 dB，在高信噪比时约高1 dB；相对误差存在类似趋势。图3、图4的仿真结果说明了改进滤波算法相对更加有效，所以后续处理中仅采用改进算法。

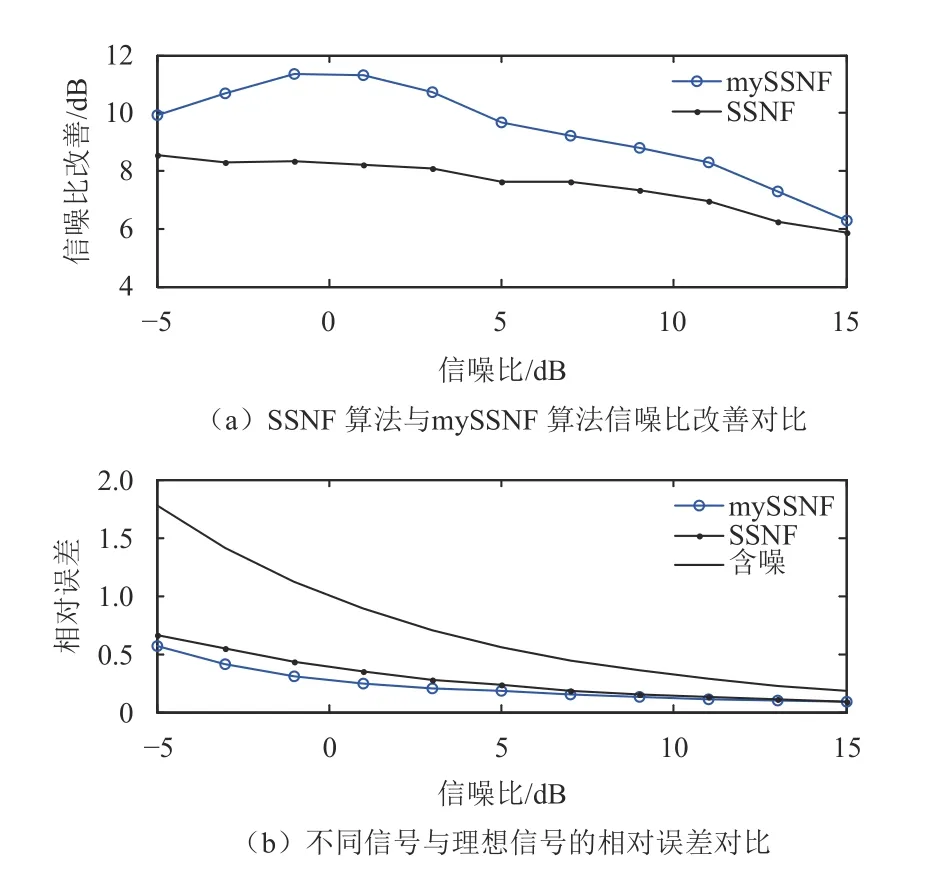
图4 传统相关滤波与改进相关滤波信噪比改善对比Fig.4 The comparison of SNR improvement after processing by SSNF and mySSNF

假设采样频率为56 MHz，信号时延真值为51Ts（采样周期），信号处理积分时间约为2.3 ms；小波分解层数为4，小波函数为db1。图5给出了滤波前后不同信噪比下群时延估计性能（蒙特卡罗仿真500次）。由图5（a）可以看出滤波前后群时延估计均值基本一致，滤波后群时延估计抖动相对较小；由图5（b）可以看出滤波后群时延估计误差有所降低，改善幅度如表1所示，可以看出滤波后群时延估计误差改善幅度最大约30%，最差约7%。图5和表1表明经过小波相关滤波后，群时延估计性能有一定程度的提高。

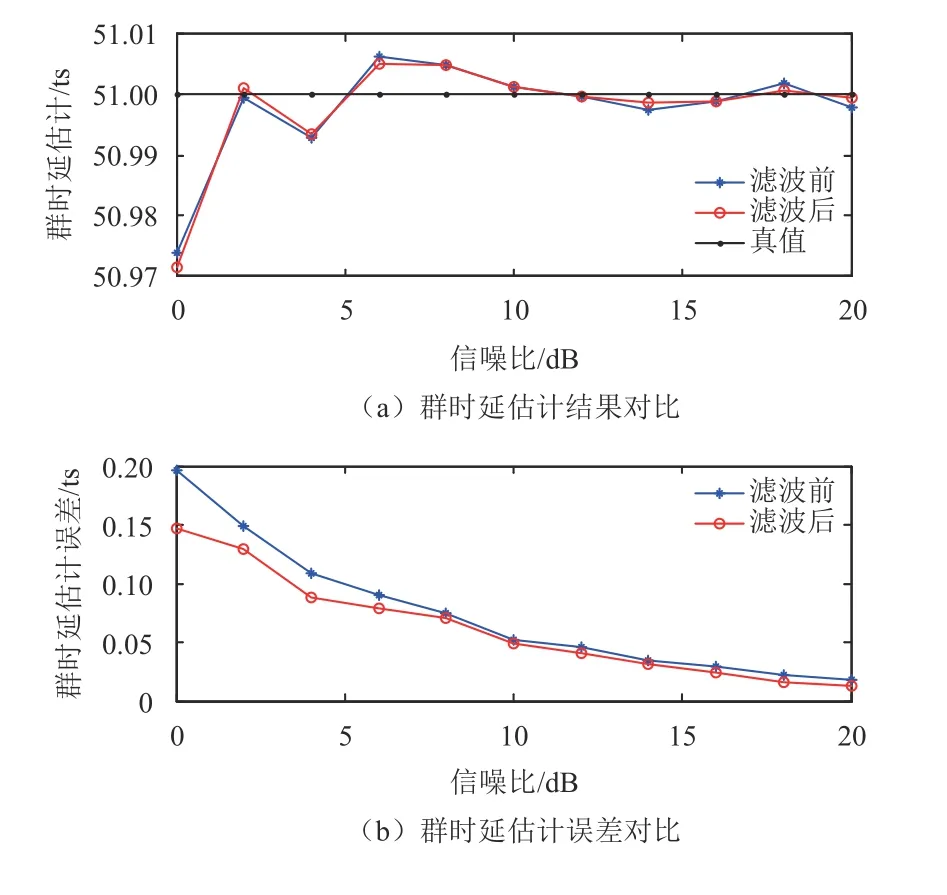
图5 mySSNF算法滤波前后群时延估计性能对比Fig.5 The comparison of group delay accuracy after processing by mySSNF

表1 滤波前后群时延估计误差改善Table 1 The improvement of group delay accuracy after processing by mySSNF

3.2 实测数据处理

实测数据为某同步卫星于2013年发射的S频段扩频测控信号，采样频率为56 MHz，宽带信号主瓣位于16～25 MHz之间，带宽约为9 MHz；考虑到信号相对幅度，拟合频率区间选为[17.5 23.5]MHz，约6 MHz；读取50段数据，每段数据时长与积分时间相等。当积分时间为9.4 ms时，图6给出了滤波前后群时延估计结果。可以看出，经过滤波后，群时延估计抖动稍有减弱。

不同积分时间下滤波前后群时延估计均值和误差如表2所示，可以看出，滤波处理后，群时延估计精度改善约10%，这与仿真信号的改善程度相当。

图6 滤波前后群时延估计结果（积分时间9.4 ms）Fig.6 The comparison of group delay accuracy after processing by mySSNF（Integration time is 9.4 ms）

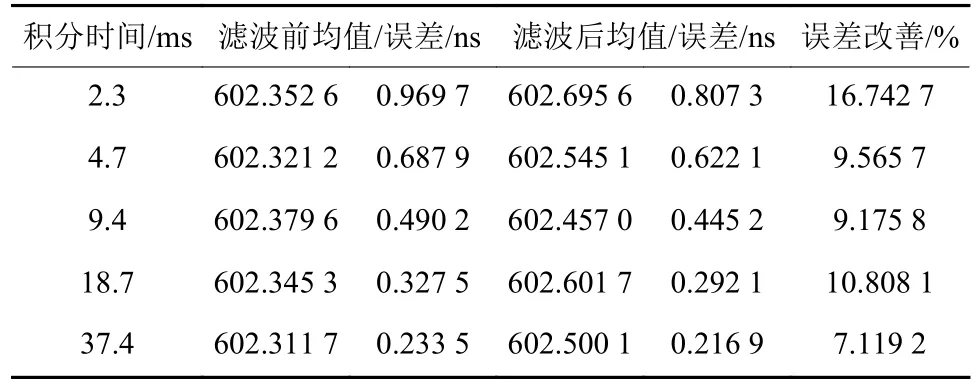
表2 滤波前后实测数据群时延估计对比Table 2 The comparison of group delay estimation without and with processing by mySSNF

4 结 论

本文针对深空探测中干涉测量微弱信号相关处理问题，提出了一种基于小波滤波的无线电干涉测量方法。首先，分析指出传统小波相关滤波算法存在小波系数在各尺度间的微小偏移降低滤波性能、低尺度小波系数易受噪声影响等问题，提出了基于移位相关、逆序处理以及最高层小波系数阈值处理的改进算法。其次，分析并构建了深空探测宽带信号模型，并给出了基于小波相关滤波的无线电测量方案，最后通过蒙特卡洛仿真和某同步卫星实测数据处理证明小波相关滤波可以改善无线电干涉测量精度。