基于LPP-LSSVM的微电网超短期负荷预测算法

马玉鑫

上海电气集团股份有限公司 中央研究院 上海 200070

1 研究背景

在微电网中应用现代信息技术、通信技术与控制技术,已经成为全球化的趋势。建立微电网,使发电设备、电网运营和终端设备互相配合,协同工作,在保证系统稳定性、可靠性的同时,使投资和对环境的影响最小[1]。负荷预测在近年来微电网的发展中扮演着极其重要的角色。系统规划与运行、收益估计、能量交易等都需要精准的负荷预测。根据预测的时间间隔,负荷预测可以分为超短期负荷预测、短期负荷预测、中期负荷预测和长期负荷预测四类,分界线一般默认为一天、两周和三年[2-4]。

由于超短期负荷预测间隔时间短,而且对于微电网而言,其负荷的波动性一般大于区域大电网,因此对预测算法的精度提出了更高要求。目前,在数据积累情况较为理想的条件下,超短期负荷预测普遍应用人工神经网络(ANN)和支持向量机(SVM),其中SVM因为引入了结构风险最小化理论,不会陷入局部极值,所以备受青睐[5-6]。实际应用中,为规避SVM复杂且耗时的二次规划求解问题,通常采用最小二乘支持向量机(LSSVM)。

早期直接应用LSSVM,可以有效解决超短期负荷预测问题,获得了比传统回归算法更好的预测结果[7-10]。众多学者为提高LSSVM的预测精度,在训练模型的输入矩阵中引入被预测日相似日的相关元素,使输入和输出矩阵间存在更强的相关性。随着微电网系统、数据采集和通信技术的发展,微电网中可收集的变量种类越来越多,采样频率也越来越快,由此对超短期负荷预测模型的训练提出了挑战。而且,在实际工程中,影响模型输出的因素并非都可以直观辨识。

可见,仅选取部分相关性较高的变量用于建模,可能会降低模型的精度。但如果将系统采集到的全部变量都作为输入用于建模,那么势必会因维度增加而导致计算成本变大,从而进一步影响预测模型的泛化能力[11]。通过引入主成分分析(PCA)消除变量间的共线性特点,然后利用SVM建模,在电力系统短期负荷预测中获得了比传统SVM更准确的预测结果[12-14]。

PCA的目标是将数据方差变化最大的方向保留下来,以此最大限度地展开数据,对于服从或接近服从高斯分布的数据集有较好的应用效果。当然,负荷数据具有较强的随机性,并且电压电流等变量明显不服从高斯分布,所以PCA在负荷数据的特征提取中会遇到信息丢失较多的问题[15]。局部保持投影(LPP)通过保持局部邻域结构完整,可以在克服上述问题的同时实现特征提取[16]。

为了解决负荷数据非高斯、高维度的问题,笔者提出一种基于LPP-LSSVM的微电网超短期负荷预测算法。算法根据天气、温度等因素选取相似日组成训练数据集,利用LPP进行特征提取,基于LSSVM训练预测模型实施负荷预测。最终,通过对某公司实际运行负荷进行试验,验证算法的有效性和优越性。

2 LPP概述

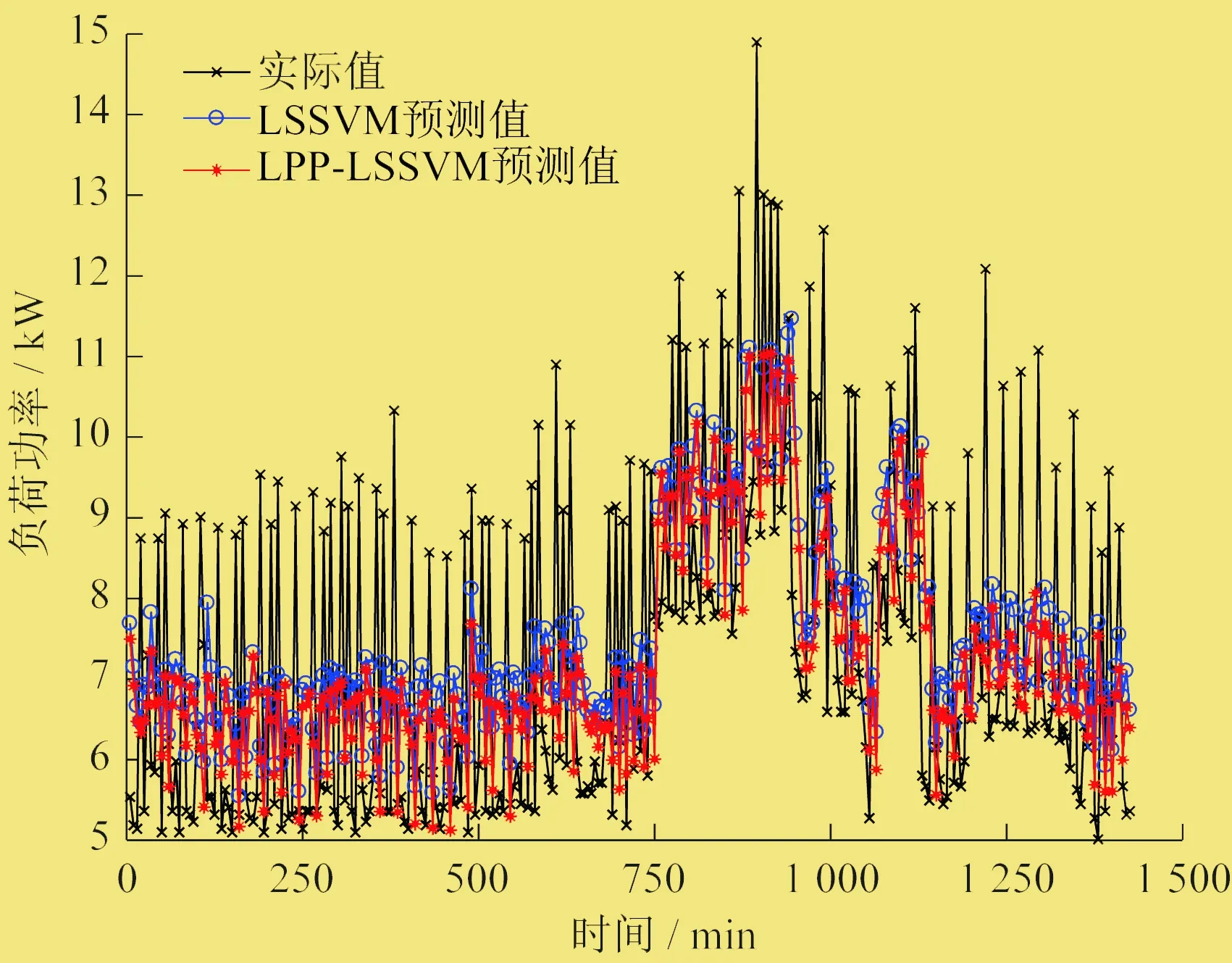
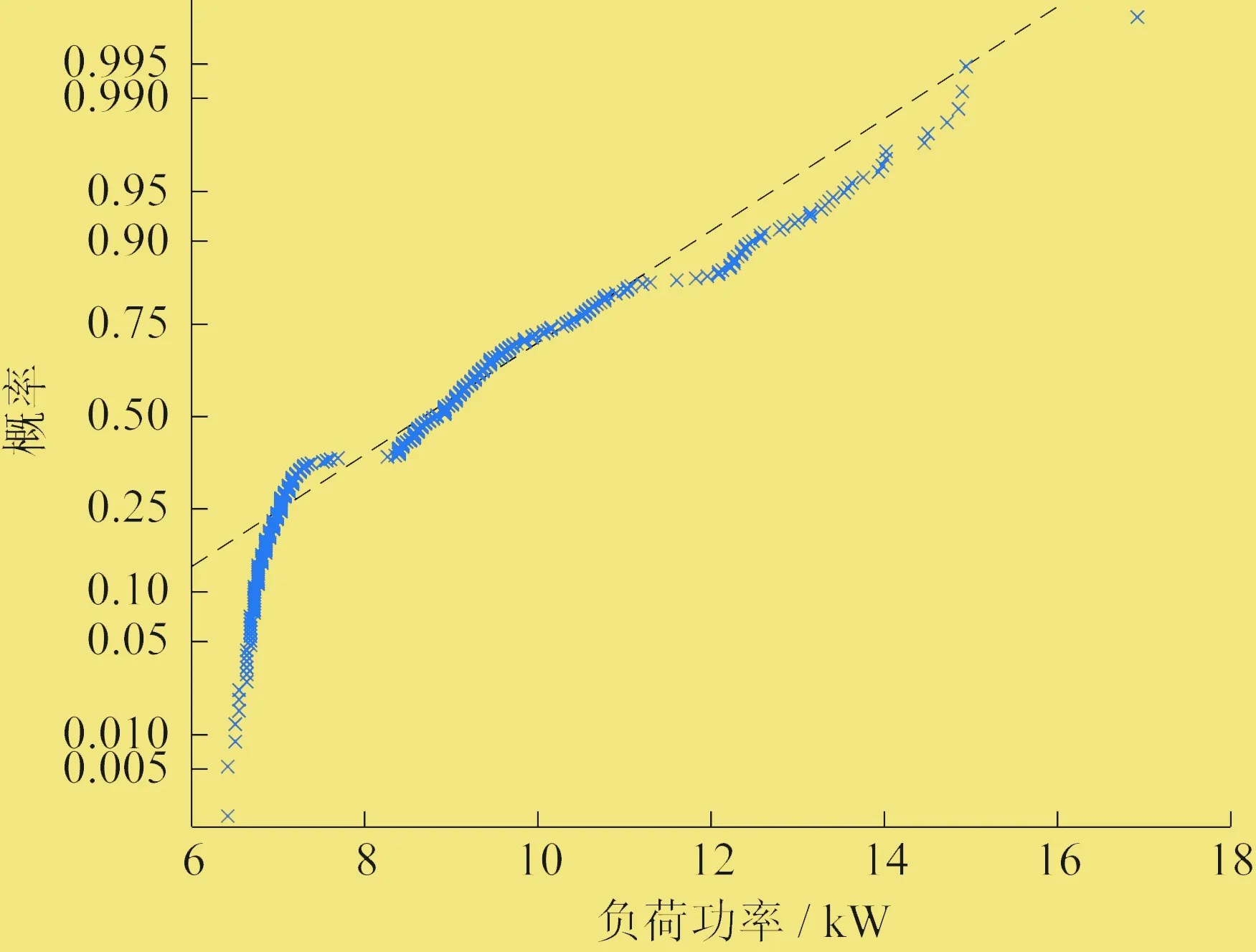
LPP可以求取一个保持数据集局部结构的投影矩阵P∈Rm×p(p

(1) 构建邻接图。根据欧几里得距离,X中每个数据xi,xj∈X(i,j=1,…,n)选择离其最近的k个数据作为邻居。若数据xj属于数据xi的k个近邻中的一个,则在节点i与节点j之间连一条直线,否则不连线。

(2) 计算权重。W为待求的权重矩阵,节点i与节点j之间权重为Wij。若节点之间无连线,则权重值设置为0。若节点之间有连线,则权重值利用高斯核函数进行设置:

(1)

式中:t为高斯核参数。

(3) 特征映射。投影矩阵P∈Rm×p(p

XTLXα=λXTDXα

(2)

(3)

L=D-W

(4)

式中:λ、α分别为特征值和特征向量;D为对角矩阵,元素值为权重矩阵的列之和。

低维数据可以表示为:

yi=xiPP=[a1,a2,…,ap]

(5)

3 LSSVM概述

建立预测模型使用的技术手段为LSSVM,其核心内容是如何确立模型的输入和输出。

SVM的基本思想是Mercer核展开定理,通过非线性映射,将输入控件的样本映射到高维的特征空间中,将寻找最优线性回归超平面的算法归结为求解约束条件下的二次规划问题,并可以求得全局最优解。设样本为m维向量,给定n个样本:

(x1,y1),(x2,y2),…,(xn,yn)∈RmR

约束于:

yi=Φ(xi)ω+b+ξii=1,…,n

(6)

式中:xi为样本输入;yi为样本输出;ω为高维特征空间的权值向量;b为偏置量;ξi为松弛因子。

用非线性映射Φ(x)将样本从原空间Rm映射到一个高维特征空间,在此高维特征空间中构造最优线性决策函数:

y(x)=ωTΦ(x)+b

(7)

利用结构风险最小化原则,确定ω、b等价于求解下面的优化问题:

(8)

式中:c为惩罚因子,c>0;RE为误差控制函数,属于不敏感损失函数。

LSSVM在优化目标中的损失函数J为松弛因子ξi的二次项,故优化问题为:

约束于:

yi=ωTΦ(xi)+b+ξii=1,…,n

(9)

用拉格朗日法求解上述优化问题:

(10)

式中:αi为拉格朗日乘子。

根据优化条件∂L/∂ω=0,∂L/∂b=0,∂L/∂ξ=0,∂L/∂α=0,有:

定义核函数Kij=K(xi,yi)=Φ(xi)Φ(yi)为高维特征内积运算,且K(xi,yi)是满足Mercer条件的对称函数,则以上优化问题转化为求解线性方程:

(15)

最后得到LSSVM的函数估计为:

(16)

4 超短期负荷预测算法

为了解决负荷数据非高斯、高维度的问题,笔者提出基于LPP-LSSVM的超短期负荷预测算法。

(1) 基于被预测日的季节类型,第一类包含1月、2月、12月,第二类包含4月、5月、6月,第三类包含7月、8月、9月,第四类包含3月、10月、11月,匹配选取h天历史数据作为总数据集。

(2) 确定负荷预测的参考历史样本点数L,即为预测T+1时刻的负荷功率,需参考T,T-1,…,T-L+1共L个时刻的负荷功率值。

(3) 构造LPP的输入数据集X=[x1,x2,…,xn]T∈Rh(s-L)×(13+L),s为每天收集的样本数,固定的13列为功率因数、电网频率、三相相电流、三相相电压、三相线电压、每日最高温、每日最低温。

(4) 使用LPP提取特征空间Y=XP,其中投影矩阵P=[a1,a2,…,ap]∈R(13+L)×p。

(5) 将标准化后的特征空间Y和负荷曲线F∈R(s-L)×(13+L)输入LSSVM,建立预测模型F=f(Y)。

(6) 对于被测日数据Xt,首先构造Yt=XtP,输入预测模型,得到T+1时刻被预测值FpT+1=f(Yt)。

(7) 计算LPP-LSSVM算法结果的平均绝对误差百分比MAPE=|FT+1-FpT+1|/FT+1×100%。

5 仿真试验

试验数据来源于上海某公司微电网示范工程。该工程配置了42 kW光伏和50 kW储能,负荷类型主要是办公楼宇和实验室,负荷波动主要来自于几个实验室的高功率设备。为了更好地配合已有的能量算法,调度储能,实现削峰填谷,拟采用笔者提出的算法代替传统的LSSVM实现超短期负荷预测。数据来自 2014年7月至2015年6月间,采样间隔为5 min,其中负荷数据主要根据各电表获取,每日最高、最低温度则参考天气预报的信息。

经过交叉验证,选取特征提取维度p为6,LPP近邻个数k为30,LSSVM惩罚因子c为10,高斯核函数参数为100。LSSVM、PCA-LSSVM、LPP-LSSVM三种算法的MAPE对比见表1。

通过表1可以看出,笔者提出的LPP-LSSVM算法在3月至11月的负荷预测中,表现均优于LSSVM和PCA-LSSVM算法。在1月、2月、12月的负荷预测中,结果较PCA-LSSVM算法略差,但优于LSSVM算法。7月、8月、9月中,三种算法的MAPE均高于其它月份,原因是夏季空调开启后负荷波动比较剧烈,进行精准预测的难度较大。

图1所示为2014年10月12日实际负荷曲线和LSSVM、LPP-LSSVM预测曲线,可以看出,LPP-LSSVM算法可以更好地反映负荷的波动情况,更接近实际的负荷曲线。LPP-LSSVM算法得到的MAPE为18.88%,相比LSSVM减小了2%。

图1 2014年10月12日负荷曲线

图2所示为2015年4月25日实际负荷曲线的高斯分布拟合结果,可以看出负荷数据明显不服从高斯分布。由于PCA自身的局限性,PCA在特征提取时会遗漏部分信息,使特征空间无法完整表达原始数据空间的结构。

图2 2015年4月25日实际负荷曲线高斯分布拟合结果

图3所示为2015年4月25日PCA-LSSVM、LPP-LSSVM预测曲线与实际负荷曲线,可以看出两种算法都能较好地预测负荷波动,但是PCA-LSSVM算法的MAPE只达到14.15%,而LPP-LSSVM算法克服了数据的非高斯和高维度问题,完整表达了负荷数据的特征,MAPE达到12.43%。

6 结论

当数据集中的某些变量服从非高斯分布时,传统PCA的相应假设将无法得到满足,于是其特征提取能力会下降,导致后续使用LSSVM建立的预测模型的精度会降低。针对这一问题,笔者提出了一种基于LPP-LSSVM的微电网超短期负荷预测算法。LPP的引入,可以保证由特征提取获得的特征空间信息精度不会因为训练数据包含复杂数学分布而受到影响。通过对上海某公司微电网实际负荷数据进行仿真试验,验证了笔者算法的有效性。

图3 2015年4月25日负荷曲线