保持尖锐特征的隐式曲线绘制算法

赵晶洁，赵瑞斌，庞明勇



保持尖锐特征的隐式曲线绘制算法

赵晶洁，赵瑞斌，庞明勇

(南京师范大学教育信息工程研究所，江苏 南京 210097)

隐式曲线在生物、医学、气象、地学、石油勘探及物探等领域有着广泛的应用。提出一种绘制带有尖锐特征的平面隐式曲线的算法，能有效地提取隐式曲线的尖锐特征。该算法首先确定曲线的绘制区域，采用自上而下的方式生成绘制区域的四叉树表示，并在四叉树节点表示的每个单元格内生成一个数值场特征点；然后连接特征点生成对偶网格；最后，利用Marching Squares算法生成曲线。实验结果表明，该算法能在网格较稀松的情况下绘制出隐式曲线，并且可以实现曲线的尖锐特征。

隐式曲线；图形绘制；可视化；移动四边形

隐式曲线的绘制工作一般包括“采样”和“构造”两个阶段[10]。采样阶段的主要任务是运用特定策略或技术采集位于隐式曲线上的点；构造阶段的目标则是将采集到的点以恰当方式连接起来，构造出分段线性的折线逼近原来的隐式曲线。目前，隐式曲线的绘制方法主要有：基于空间剖分的方法[11]、基于连续性的方法[12]、以及基于物理模拟的方法[13]等几类。在基于空间剖分的方法中，最为经典流行的是被称为Marching Squares (MS)的方法[14]，其是可视化领域中著名的Marching Cube方法的二维特例。该方法利用了隐式曲线的一个良好性质，即的隐式曲线是平面2上分别满足()>0和()<0的2个点集的边界。对于平面上的任一线段，若其2端点处的隐函数值异号，则该线段上至少有的一个零点，可采用二分迭代法或插值法逼近该零点。在绘制隐式曲线的过程中，①在绘制区域上构造一个四边形格网；②计算各个格网顶点处的隐函数值，并确定每个格网边上可能存在的零点；③用线段连接格网中每个四边形的不同边上的零点，且逼近隐式曲线在该四边形内的部分，从而在绘制区域中绘制出隐式曲线。为了实现隐式曲线的精细化绘制，往往需要构造高密度的格网，这会带来巨大计算量[15]。为了降低计算量，学者们提出了空间自适应剖分方法，即先在绘制区域中构造低密度格网，再对各个包含曲线的四边形进行自适应细分，并用四叉树数据结构存储平面区域的细分数据，从而消除部分冗余计算，从而降低了绘制过程中的总计算量。基于连续性的方法一般利用空间和曲线的连续性特性，通过分析隐式曲线的切向、曲率等局部几何性质来实现曲线的绘制[16]。如文献[17]的算法首先找到隐式曲线上的一个点，然后以该点为中心构造一个正方形，再根据隐式曲线与该正方形四条边的相交情况，不断向四周扩展出新的四条边，最后通过对隐式曲线在各四边形内的部分进行线性化处理，构造出整条隐式曲线(图1(a))。文献[18]则从曲线上的一点出发，根据曲线的局部曲率大小沿曲线在该点处的切向前进一定的距离，此过程称为预测；再根据函数定义的梯度方向，将预测的新点以投射方式“更正”到曲线上，然后从新点出发，重复“预测-更正”过程，从而绘制出整条曲线(图1(b))。基于物理模拟的方法将隐函数视为二维空间的数值场函数，然后采用模拟某种物理过程来驱动采样点运动，最终实现曲线的优化绘制。如文献[19]用一条封闭折线包围隐式曲线，然后通过场函数移动折线上的点，使之迭代“收缩”到隐式曲线上。文献[20]提出采用粒子系统在曲线上采样，所得到的采样点在曲线上的分布是优化的。

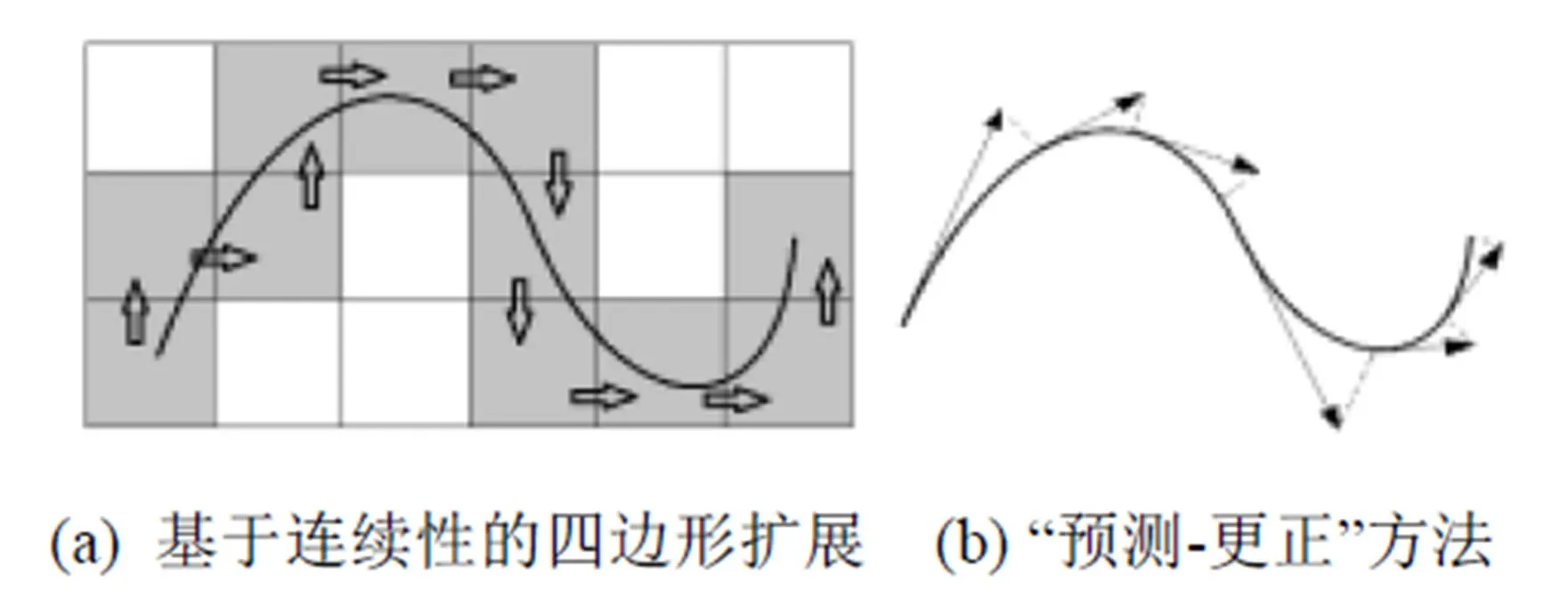
图1 2种基于连续性的隐式曲线绘制方法

当隐式曲线是连续光滑的，或隐函数数值场平滑变化时，现有方法均能很好地工作。但当隐式曲线上具有尖锐特征或数值场局部变化剧烈时，基于空间剖分的方法往往不能捕捉到相应的尖锐特征，而基于连续性与基于物理模拟的方法通常不能鲁棒地工作。另一方面，在医学、地学等领域中，有大量的应用涉及到带有尖锐特征的隐式曲线的绘制需求。

针对上述问题，本文提出一种保持隐式曲线尖锐特征的绘制算法。算法以MS技术为基础，采用自适应剖分方法来减少冗余数据，其特别之处在于，通过引入数值最优化技术等实现曲线上尖锐特征的捕捉，最终绘制出带有尖锐特征的隐式曲线。与现有方法相比，本文算法不但能够有效地保持隐式曲线上的尖锐特征，而且其在处理不同隐式曲线时，具有较好的鲁棒性。

1 算法梗概

图2 绘制区域上两种不同四边形格网的构造方法

图3 单元格内特征点与采样点的关系

步骤4. 生成对偶网格。对于提取到的特征点，根据其所在四叉树单元与邻近其他单元之间的毗邻关系，使用文献[21]提出的遍历算法构造自适应细分四叉树网格的对偶网格。其中，对偶网格的顶点为数值场的特征点。上述毗邻关系决定了对偶网格顶点间的拓扑连接。

步骤5. 隐式曲线的逼近与绘制。对于对偶网格中的每个单元，基于MS方法对其内部的隐式曲线进行分段线性离散逼近，从而实现隐式曲线的绘制。

2 算法步骤

本文算法主要包含4个步骤，本节将分别对其进行详细讨论。

2.1 构造自适应细分四叉树平面剖分结构

为了进一步逼近隐式曲线并降低计算复杂度，在均匀四叉树的基础上，定义了如下细分规则并进一步构造自适应细分的四叉树结构。

(1) 对于均匀四叉树中的每个节点，将其4个顶点分别代入，得到4个隐函数值。如果这4个值均为正或均为负，则认为该节点具有一致的顶点符号，同时隐式曲线不经过该节点且无需对其继续细分。

2.2 提取隐函数数值场特征点

为了逼近隐式曲线并突出其尖锐特征，本文算法将视为二元数值场函数，并借助计算数值场的特征来探测隐式曲线的特征。算法在已构造自适应细分四叉树的基础上，通过对四叉树的每个叶子节点进行数值场特征探测生成一个对应的特征点。

本文隐式曲线特征点的提取，基于如下发现：给定一个四叉树叶子节点，对于经过该节点中的采样点且以在该采样点处的梯度方向为法向的每条直线，其在该节点内特征点处的值与在特征点处的值之间存在误差，把每个误差叠加，所得的误差和最小。因此，可根据上述发现构造一个二次误差函数(quadratic error functions，QEF)来求取每个叶子节点中的特征点。QEF定义如下

其中，是采样点数量；T()是经过采样点且以在该采样点处的梯度方向为法向的直线在特征点处的值，其可表示为

其中，为采样点；T()为在采样点p处的梯度；(,)为采样点与特征点之间的距离。

为了更直观地说明上述原理，图3给出了一个一维情况下的特例。其中，曲线为数值场；1和2为2个采样点；虚线1，2分别为经过1和2，且以隐函数在1和2处的梯度方向为法线的直线；如果在轴上选择2个点3和4，可以发现，在3点处1(3)与(3)之间的差值为0，而在4点处的差值为(4)–(4)。如果在轴上选取除3外任意一点，该点处的差值都会大于0，在3点处，差值最小。由图3可知，场曲线在3点处呈现出尖角特征，即3是该数值场的特征点。因此，可通过最小化QEF找到场特征点。

本文算法通过如下步骤提取特征点：

步骤1. 对于自适应细分四叉树中的每个叶子节点，将其4个顶点看作采样点；

步骤2. 将采样点代入QEF函数，定义每个采样点的T()与()之间的误差平方和；

步骤3. 通过最小化值确定特征点的位置。

2.3 创建对偶网格

在构建隐式曲线时，传统的MS算法通过连接在网格中的零点来逼近隐式曲线在该网格单元内的部分。然而，若曲线在该单元中有尖锐特征，则该方法往往会丢失这些特征。为此，本文算法通过连接自适应细分四叉树中的特征点来创建对偶网格。其能够逼近隐式曲线的形状并有效保留曲线的尖锐特征。基于以下3个规则来创建对偶网格：

(1) 若自适应细分四叉树中，一个节点的4个孩子节点均为叶子节点，则将该4个孩子节点中的特征点依次相连，生成一个单元格，参见图4(a)；

(2) 对于两个相邻节点，如果一个是叶子节点，一个是非叶子节点，算法首先查找到非叶子节点中的所有叶子节点，然后将最初的叶子节点与相邻的新查找到的叶子节点的特征点依次相连组成一个单元格，参见图4(b)；

(3) 如图4(c)所示，对于2个具有相同边界的非叶子节点，算法首先分别遍历并找到其所对应的所有叶子节点，然后将相同边界周围的叶子节点依次相连组成新单元格。

根据上述3个规则，通过对自适应细分四叉树每个节点内的特征点依次相连，构造出一个对偶网格，如图5所示。

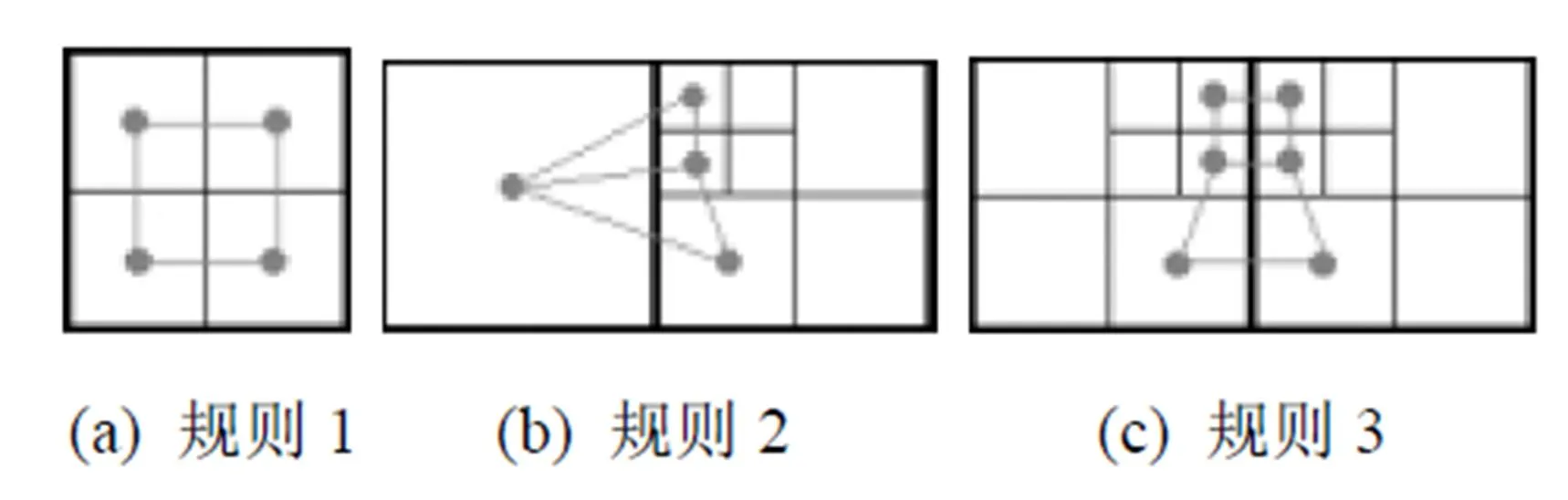
图4 创建对偶网格的3个规则

图5 对偶网格示意图

2.4 绘制曲线

在构造对偶网格的基础上，本文算法借助经典的MS算法实现隐式曲线的绘制。由于在绘制曲线时MS算法通常在形状规则的四边形上操作，而本文算法所创建的对偶网格中，既有不规则的四边形又有三角形。因此，算法将对偶网格中的每个单元格在拓扑上等同于四边形，再运用MS算法绘制隐式曲线。本文算法首先判断对偶网格单元格的每条边上是否存在隐函数的零点，然后对于有零点的边则通过线性插值确定零点位置，最后依次连接单元格上的零点逼近隐式曲线在该单元格内的部分，从而绘制出隐式曲线。

对于MS中可能出现的二义性问题，本文算法对有二义性的单元格进行三角分割，求出单元格对角线上的中点坐标以及其在该中点的函数值，该点与其他4个顶点构成4个三角形。因为在三角形中总有1个顶点的符号与其他2个不同，所以可以避免二义性，如图6所示。

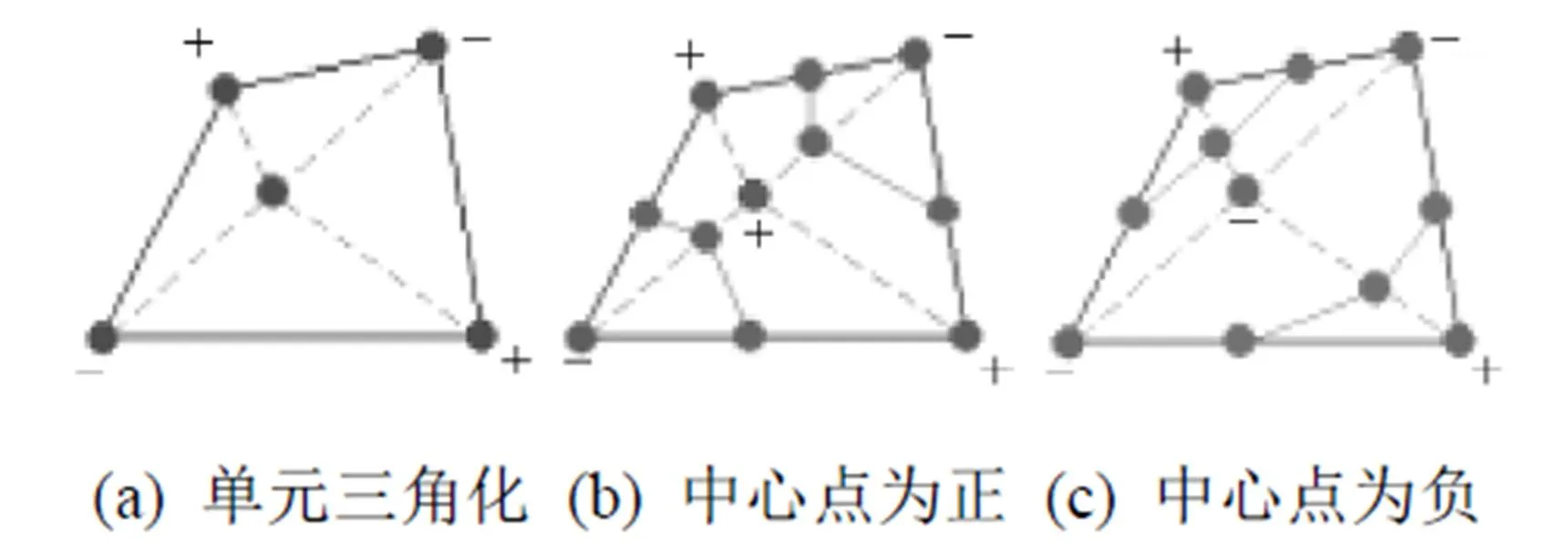
图6 MS中二义性情况处理示意

由于在对偶网格的创建过程中，对偶网格的顶点位于函数的数值场特征上，所以本文算法所绘制的隐式曲线能有效地保留尖锐特征。

3 实验与结果

为了验证本文算法的鲁棒性和准确性，本文使用Dev C++和OpenGL图形库在Windows平台上实现了本文算法。并采用如下5个隐式曲线进行曲线绘制的测试，并将绘制结果与传统的MS算法以及文献[22]中的算法在二维图形上的运行结果进行了比较。

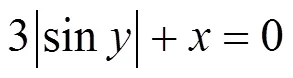
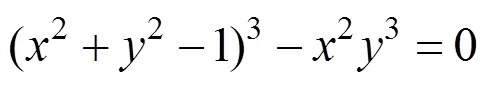
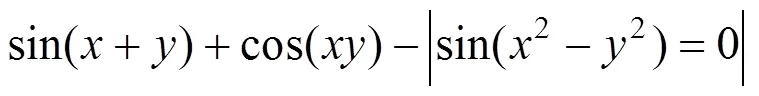
对比图7中给出的3种方法的绘制结果，可以发现：①传统的MS方法(下文统称方法1)明显会丢失了原始隐式曲线上的尖锐特征。如图7所示，第1行中所绘制出的曲线均未能有效地捕捉到相应的尖锐特征，曲线上的尖锐特征被钝化处理；②文献[22]中的方法(下文统称方法2)只保留了原曲线的部分尖锐特征，且所保留的尖锐特征精确度不够。如图7所示，第2行中所绘制的曲线没有准确捕捉到相应的尖锐特征，如该行第1列中的曲线理论上应绘制出“V”形局部，但该曲线明显丢失了尖角特征；③相比于方法2，本文算法能准确捕捉到曲线的尖锐特征。图7第3行中所绘制的曲线所示，所有曲线均保留了尖锐特征，例如该行第一列中的曲线呈现出尖角特征，逼近于“V”形，比较准确地绘制出了隐式曲线。

表1 3种算法性能效果对比

曲线网格行列数/四叉树深度线段数计算时间(s) MS方法文献[22]方法本文方法MS方法文献[22]方法本文方法MS方法文献[22]方法本文方法 式(3)23881915150.018 8590.016 0930.016 465 式(4)26661 1545185400.492 5310.087 5550.089 490 式(5)26661 4195656000.544 8910.282 2330.314 777 式(6)255521388880.384 6640.345 3090.382 034 式(7)26661 0962673290.453 8320.374 1450.382 160

图7 不同算法对各函数曲线的绘制结果

在性能方面，对比表1数据可知: 在网格深度相同的情况下，方法2与本文算法绘制曲线所用的线段数少于方法1，并且这2种方法运行速度均快于方法1。当隐式曲线比较复杂时，本文算法需要耗费额外的时间来精确计算数值场的特征点，除此之外，利用这些特征点生成对偶网格也需要额外的时间，所以相对于方法2，本文算法生成曲线的速度较慢。

4 结束语

本文提出一种能保持尖锐特征的隐式曲线绘制算法。算法通过构造QEF定位、捕捉隐函数数值场的特征点来捕捉隐式曲线的特征，通过连接特征点生成对偶网格来逼近了隐式曲线的形状。实验表明，本文算法能在较稀松的网格中捕捉隐函数数值场的特征点，并且能在由这些特征点构建的对偶网格中提取出较为精确的曲线，提升了曲线的绘制精确性。

为了逼近隐式曲线并且保留曲线的尖锐特征，本文算法需要生成自适应细分四叉树以及对偶网格，因此算法的运行时间较长。若要解决此问题，可开发只在包含曲线的单元格内提取特征点或者创建对偶网格的算法，预计该算法会提高运算速度。

[1] 徐国良. CAGD中的隐式曲线与曲面[J]. 数值计算与计算机应用, 1997, 18(2): 114-124.

[2] BLOOMENTHAL J. An implicit surface polygonizer [M]. San Diego: Academic Press, 1994: 324-349.

[3] SHELBERG M C, MOELLERING H, LAM N. Measuring the fractal dimensions of empirical cartographic curves [M]. Rome: Food and Agriculture Organization of the United Nation, 1982: 481-490.

[4] 赵伟, 赵卓宁, 李五生. 一种有效的离散数据场等值线生成方法[J]. 成都信息工程学院学报, 2007, 22(1): 116-121.

[5] 温维亮, 郭新宇, 陆声链, 等. 隐式曲面在三维植物建模中的应用研究综述[J]. 图学学报, 2010, 31(3): 1-10.

[6] SUNDARAMOORTHI G, YEZZI A, MENNUCCI A. Coarse-to-fine segmentation and tracking using Sobolev active contours [J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2008, 30(5): 851-864.

[7] 寿华好, 何苹, 缪永伟. 自动微分在隐式曲线绘制中的应用[C]//第四届全国几何设计与计算学术会议. 北京: 中国工业与应用数学学会, 2009: 150-153.

[8] 李华, 蒙培生, 王乘. 医学图像重建MC算法三角片的合并与实现[J]. 计算机应用, 2003, 23(6): 104-106.

[9] 李彩云, 朱春钢, 王仁宏. 参数曲线的分段近似隐式化[J]. 高校应用数学学报A辑, 2010, 25(2): 202-210.

[10] 骆沛, 吴壮志, 夏春和, 等. 基于e1范数最小化的非流形曲线族重构[J]. 计算机学报, 2013, 36(9): 1917- 1928.

[11] LAGUARDIA J J, CUETO E, DOBLARE M. A natural neighbour Galerkin method with quadtree structure [J]. International Journal for Numerical Methods in Engineering, 2006, 15(5): 529-548.

[12] ZHU X J, JI L X, JIN X B. Fitting and reconstruction of three-dimensional curve based on orthogonal curvature [C]//2009 9th International Conference on Electronic Measurement and Instruments. New York: IEEE Press, 2009: 323-328.

[13] 李云夕, 冯结青, 金小刚. 基于有向距离场的代数B-样条曲线重建[J]. 软件学报, 2007, 18(9): 2306-2317.

[14] MAPLE C. Geometric designing and space planning using the marching squares and marching cube algorithms [C]//2003 International Conference on Geometric Modeling and Graphics. New York: IEEE Press, 2003: 90-95.

[15] MANTZ H, JACOBS K, MECKE K. Utilizing Minkowski functionals for image analysis: a marching square algorithm [J]. Journal of Statistical Mechanics Theory and Experiment, 2008, 12 (12): 12015.

[16] 肖海, 章亚男, 沈林勇, 等. 光纤光栅曲线重建算法中的曲率连续化研究[J]. 仪器仪表学报, 2016, 17(5): 993-999.

[17] CIPOLLETTI M P, DELRIEUX C A, PERILLO G M E, et al. Superresolution border segmentation and measurement in remote sensing images [J]. Computers and Geosciences, 2012, 40(3): 87-96.

[18] AKKOUCHE S, GALIN E. Adaptive implicit surface polygonization using marching triangles [J]. Computer Graphics Forum, 2001, 20(2): 67-80.

[19] 刘颖. 复杂的隐式函数曲线绘制算法的研究[D]. 长春: 吉林大学, 2006.

[20] 范丽鹏, 王丽英, 庞明勇. 平面简单闭合曲线离散采样与重建算法[J]. 图学学报, 2015, 36(4): 511-515.

[21] JU T, LOSASSO F, SCHAEFER S, et al. Dual contouring of Hermite data [J]. ACM Transactions on Graphics, 2002, 21(3): 339-346.

[22] RAMAN S, WENGER R. Quality isosurface mesh generation using an extended marching cubes look up table [J]. Computer Graphics Forum, 2010, 27(3): 791-798.

An Algorithm for Visualizing Implicit Curves with Sharp Features

ZHAO Jing-jie, ZHAO Rui-bin, PANG Ming-yong

(Institute of EduInfo Science and Engineering, Nanjing Normal University, Nanjing Jiangsu 210097, China)

Implicit curve plays an essential role in the fields of medicine, meteorology, geology, petroleum exploration, geophysics and so on. In this paper, we propose an algorithm to visualize implicit curves with sharp features, which can effectively extract the sharp features of such curves. The algorithm first defines the visualizing area of the curve and then adopts a quadtree that generates visualizing area by a top-down method. In each cell, the method produces a feature point of the numerical field, and connects different feature points to generate the dual mesh. Finally, the algorithm employs the Marching Squares algorithm to generate the curves. Experiments show that our method can efficiently extract the sharp features of implicit curves, and it can work with various implicit curves with or without sharp features robustly.

implicit curve; graphic plotting; visualization; marching squares

TP 391

10.11996/JG.j.2095-302X.2019020373

A

2095-302X(2019)02-0373-06

2018-06-21；

2018-09-12

全国教育科学“十三五”规划教育部重点课题(DCA170302)；江苏省社会科学基金项目(15TQB005)

赵晶洁(1994-)，女，山西晋城人，硕士研究生。主要研究方向为数字媒体技术。E-mail：Ginjer@yeah.net

庞明勇(1968-)，男，安徽淮南人，教授，博士，博士生导师。主要研究方向为几何建模与数字几何处理。E-mail：panion@netease.com