基于相似模型试验的导管架平台有限元模型修正

林 红, 李 萍, 杨 蕾, 齐 宝, 陈新雅, 陈国明

(1.中国石油大学(华东)海洋油气装备与安全技术研究中心, 山东青岛 266580; 2.中国石油大学(华东)储运与 建筑工程学院, 山东青岛 266580; 3.中国石油大学(华东)理学院,山东青岛 266580)

海洋平台长期服役在恶劣的海洋环境中,除受到风、浪、流等环境载荷,还可能遭受地震、火灾、船舶碰撞等突发载荷的作用[1-2],因此为保证服役海洋平台结构的安全运行,定期对结构的安全性进行动态评价十分必要。其中一个能准确代表平台结构实际情况的有限元分析模型是结构安全评估的先决条件。然而,由于海洋平台结构的复杂性及在建立有限元模型过程中的各种不确定性、理想化假定及简化等因素,导致根据设计尺寸等建立的有限元模型与实际结构之间不可避免地存在一定偏差[3-4]。同时服役多年的平台结构很易发生腐蚀、疲劳和局部屈曲、断裂等损伤,也会导致服役结构的物理参数存在着潜在的不稳定因素[5]。为实现在役平台结构的服役状态和生存能力的精确评估,非常有必要根据监测、检测数据对结构的初始有限元模型进行必要的修正,以提高有限元分析结果的精度和可信度。近年来,有限元模型修正[6-8]方法和技术已逐渐成为研究的热点问题,尤其在桥梁、飞机等工程结构的有限元模型修正方面[9-11]取得较大的进展。在海洋工程领域,刘爱霞等[12]将有限元模型修正思想引入简化的导管架平台结构,并重点修正了地基弹性支承的参数;李英超等[13-14]引入交叉模型交叉模态(CMCM)方法,并将其进行了发展。目前,虽然中国已有海洋平台安装了健康监测系统,但尚未有效利用采集到的海量数据为平台结构的状态评估和安全运行提供科学依据,对于复杂海洋平台结构的有限元模型修正方法和应用研究,仍存在较多困难。基于此,笔者针对完好平台及损伤平台两种结构,提出基于相似模型模态试验的有限元模型修正方法。根据相似原理设计制作缩尺试验模型,展开模态试验并根据模态测量值识别结构的模态特征。采用ANSYS进行平台有限元模型的模态计算,并根据模态置信准则(MAC)分析试验数据和有限元模拟模态数据的相关性。将优化方法引入含有未知损伤的海洋平台有限元模型修正问题,采用结构参数的优化方法识别损伤位置,并以含有构件缺失的试验模型为例对其有限元模型进行优化,从而实现损伤平台结构有限元模型的更新。

1 力锤激振下平台相似模型模态试验

1.1 平台相似模型的设计制作

所研究海洋平台为4桩腿4层导管架结构,每层均有横撑且最下面两层设置有K型斜撑,该平台的实际设计高度为29.5 m,质量为270 t。导管架平台的试验模型须根据相似原理[15]进行设计,严格根据几何相似、刚度相似和质量相似准则,设计并制作了1∶25的缩尺试验模型,如图1所示,导管架主体采用不锈钢材料焊接而成。

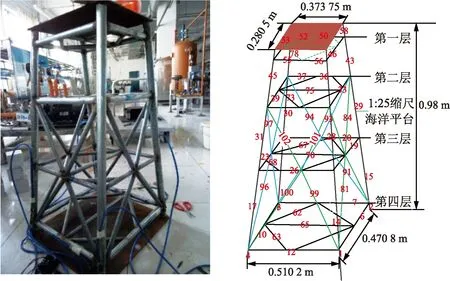
图1 缩尺试验模型Fig.1 Scaled experimental model description

首先,由几何相似条件确定缩尺模型的几何尺寸:

sl=1∶25.

(1)

其中,sl为几何比,表示缩尺模型与实际结构的几何尺寸之比。由此,计算出缩尺模型的高度为0.99 m,其他尺寸如图1所示。

其次,由刚度相似条件确定缩尺模型中钢管的直径和壁厚。根据相似原理,有

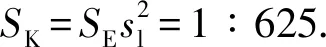
(2)

式中,SE和SK分别为弹性模量比及刚度比,分别表示缩尺模型与实际结构的弹性模量之比和刚度之比。

由此,计算出缩尺模型中主要钢管的直径和壁厚,同时考虑市场上可供选择的钢管型号,确定缩尺模型中所用的主要钢管的尺寸如表1所示。

表1 缩尺模型主要钢管的直径和壁厚
Table 1 Diameters and wall thicknesses of mainpipes in scaled model

mm

由质量相似比sn确定试验模型的质量为

(3)

式中，sn为缩尺模型与原结构质量之比。

由此,计算出缩尺模型的理论质量为17.28 kg,加工后试验模型称重为17.3 kg。

1.2 模态试验装置及测点布置

试验模型不仅要满足与原型几何尺寸、质量及刚度等物理参数相似,更要保证其动力学特征相似。为获取该缩尺模型的动态特征,进行了模态试验,提取其模态参数。试验装置见图2,试验中用到的仪器设备包括:带力传感器的力锤1个、带磁座的加速度计5个、一台包含2通道电荷放大器和16通道USB接口信号采集的锤击测试仪。

图2 缩尺导管架模型的模态试验装置Fig.2 Modal experiment equipment for scaled jacket model

用钢帽力锤作为激振器[16],锤击时,顶帽与试验结构发生冲击接触,对结构施加一个瞬态的冲击力。将加速度计固定在可能产生较大响应的测点处,即缩尺模型顶部的两个对角点;力锤敲击位置则选另一个角点,如图2(a)所示。依次用大小近似相等的水平力分别在X方向和Y方向各敲击10次,通过单点输入多点输出的模态参数测试方法[17],得出多组时域信号。每次用力锤敲击完成后等待数秒,待采集的信号变化曲线和数值稳定后,再进行数据的保存和记录,随后进行下一次敲击。

1.3 模态参数辨识

对于加速度传感器的采样数据首先进行降噪预处理,以减小噪声对试验结果的影响,常用的降噪方法有平滑处理和消除多项式趋势项处理[18]两种方法。其中平滑处理法(又称滑动平均法)主要为了消除噪声信号,而消除多项式趋势项方法主要消除外部环境对加速度信号采集仪器的干扰。由于本试验中噪声影响比外部温度等对信号采集仪器的干扰作用大得多,因此选择五点滑动平均法对采样数据进行降噪处理,图3为用滑动平均法处理前后的加速度信号。

对于通过预处理的加速度信号,通常可采用复指数法(Prony法)或ARMA时间序列分析法进行模态参数识别[18],其中复指数法是用一组指数项的线性组合来拟合等间距采样数据的方法,可从中得到结构的阻尼比、固有频率等信息;ARMA法的原理是通过参数模型对试验数据进行处理来识别模态参数。将两种方法的结果绘制于图4。

图3 五点滑动平均法处理加速度信号Fig.3 Acceleration signal smoothing by five point moving average method

由图4看出,两种方法计算得出的拟合曲线与振动信号预处理曲线均能很好地拟合。选用复指数法计算前十阶模态频率,并通过阻尼比删除法和稳定图法[19]对模态频率筛选,最终得出X向、Y向敲击的前六阶固有频率分别为:56.72、65.80、119.35、240.27、268.06、282.38,及58.85、66.59、121.23、239.27、262.06、276.38 Hz。理论上,X向敲击、Y向敲击的试验数据应该一样,而试验中由于噪声及力锤敲击力等影响,会使两者产生一定误差,但该误差仍在允许范围内。

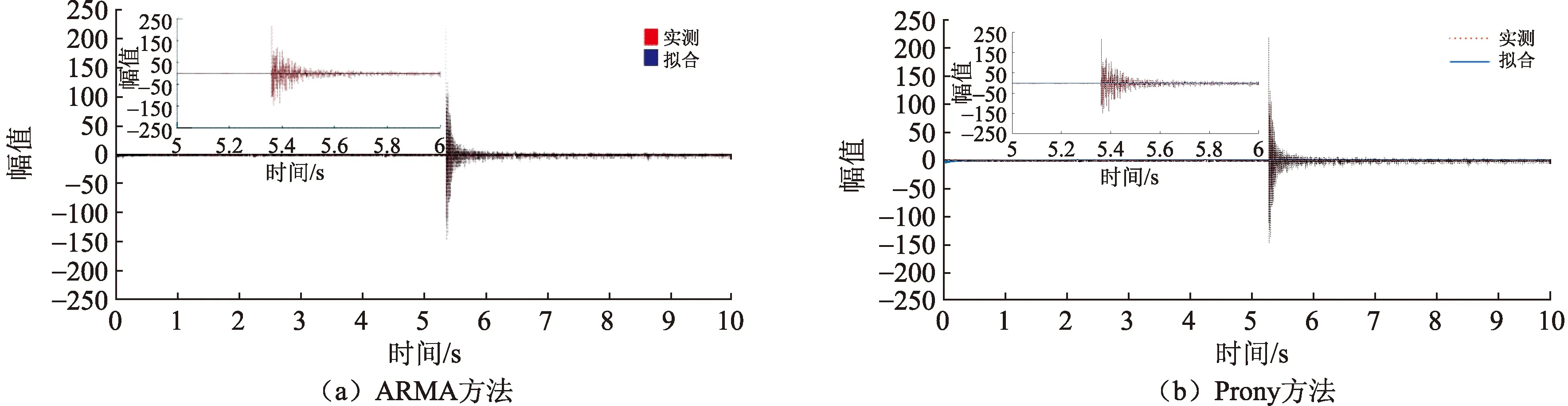
图4 模态参数识别Fig.4 Modal parameter identification

2 缩尺平台有限元模型的模态计算及相关性分析

2.1 有限元模型的模态计算

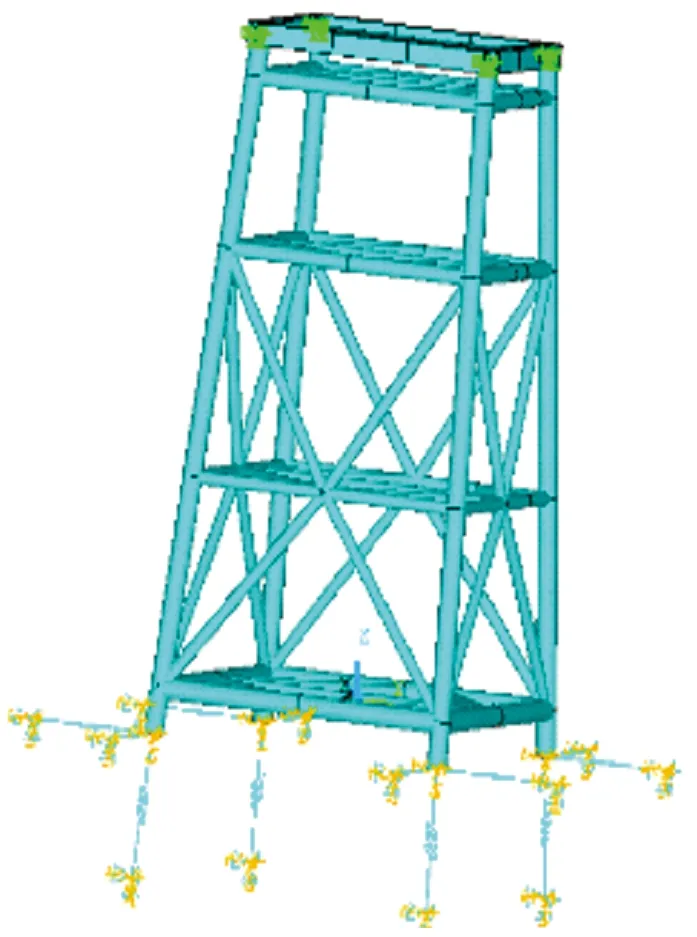
图5 缩尺导管架有限元模型Fig.5 Finite element model of scaled jacket

基于有限元软件ANSYS建立缩尺导管架平台的有限元模型如图5所示。桩腿采用pipe16单元,甲板用shell63单元,桩腿和甲板连接处采用beam4单元,底部桩腿插入海底部分采用combin14弹簧单元并通过设置3个方向弹簧单元的刚度模拟平台底部的管-土相互作用。导管架结构选用A3不锈钢材料,弹性模量取为200 GPa、密度为7 800 kg/m3、泊松比为0.3。采用Block Lanczos法对该导管架模型的动力特性进行分析,获得导管架模型的前六阶模态固有频率分别为66.69、74.58、107.56、301.98、320.50和326.76 Hz。

2.2 模态置信准则及相关性分析

由于结构的复杂性和不确定性,有限元模型无法真实、可靠地表示实际结构,有限元模型修正的目的即是根据试验模型的模态测试结果对初始有限元模型进行调整,使得有限元模型的模拟结果与试验结果相一致。在本文中仅选取了前6阶低阶频率进行有限元模型的修正,为了研究试验数据和有限元计算得出的模态数据的相关性,采用模态置信准则(MAC)[20]进行评价,表示为

(4)

式中,MACij为第i阶试验振型与第j阶有限元振型之间的相关系数;Φi为第i阶试验振型;Φj为第j阶有限元振型。MAC数值越大表明振型之间的相关性越大,若MAC数值接近于1则表明相关性非常好,反之若数值接近于0则表明相关性非常差。

表2列出了缩尺模型模态试验测量得到的前六阶固有频率及ANSYS有限元计算得到的前六阶固有频率。可见,有限元模型修正前最大误差为26.21%;而MAC最大值为0.94,MAC最小值为0.83,MAC平均值为0.90,这表明匹配情况较好。

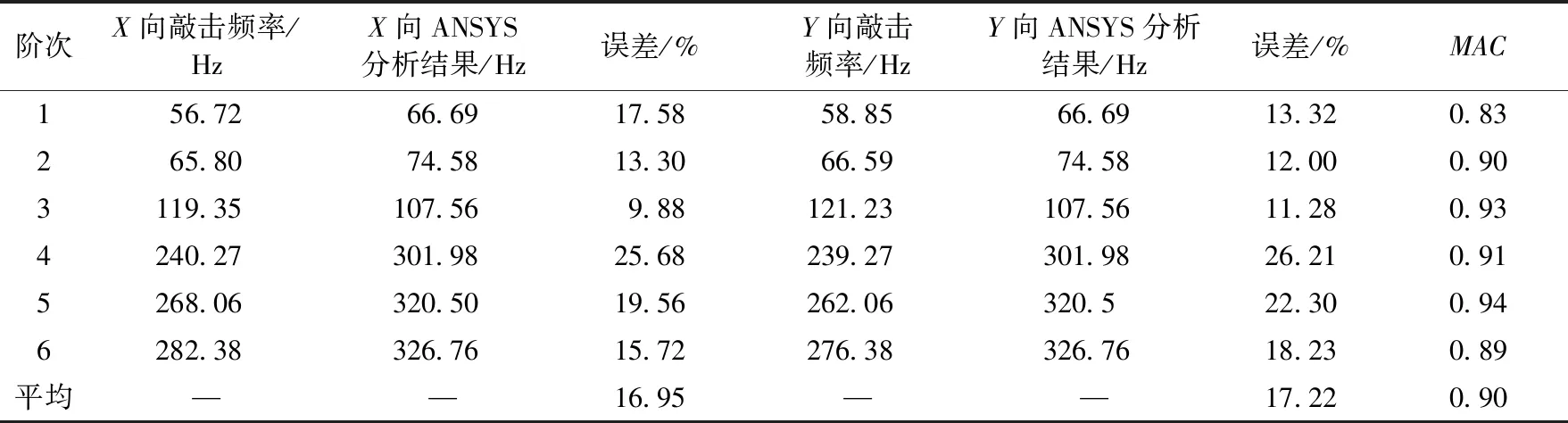
表2 前6阶频率的试验结果与有限元模拟结果及其相关性

3 导管架有限元模型修正理论

3.1 有限元模型修正理论

有限元模型与试验模型不一致的原因主要由模型结构误差、阶次误差及参数误差引起。在有限元模型修正过程中,如何从众多参数中有效选择待修正的参数至关重要。通常认为,这3种误差中参数误差是有限元模型误差的主要原因,并假定参数误差可通过边界条件、材料参数、几何参数等来修正。修正参数选定后,有限元模型修正问题可转变成为对结构参数的优化问题,且往往为含有一定约束条件的约束优化问题[21]。图6给出了有限元模型修正的一般流程。

图6 有限元模型修正流程Fig.6 Flow chart of finite element model updating

3.2 灵敏度分析

待修正参数的选择对提高修正模型与试验模型的相似度非常重要。一般情况下可考虑将边界条件、弹性模量、密度、板厚、壁厚、截面面积等设计变量作为待修正的参数。

目标函数f设置为(即考虑前六阶固有频率的相对误差平方和均值最小)

(5)

式中,ge,i和gs,i分别为各阶固有频率的试验测量值和有限元模拟值,i=1,2,…,6;x=(x1,x2,…,xn)为n个设计变量组成的向量。

选取结构的各阶固有频率的有限元模拟值gs,i作为修正模型的状态变量,则目标函数及状态变量对设计变量的灵敏度[21]定义为

式中,xj为设计变量(j=1,2,…,n);为目标函数及状态变量对设计变量的梯度向量。

3.3 考虑参数约束的优化分析法

采用优化求解法对有限元模型进行修正,则在迭代过程中当目标函数最小时,有限元模型与实际结构的动力特性之间的差别也最小。

带有约束条件的优化问题的数学表述如下:

(6)

式中,f为目标函数;xj为设计变量;n为设计变量数目;gs,i(i=1,2,…,6)为状态变量,表示1～6阶频率的模拟值。

上述优化分析迭代收敛的条件设置为

(7)

式中,ε为给定精度,对于完整试验模型和损伤试验模型,ε可分别取为0.052和0.12。

4 导管架有限元模型修正结果及讨论

4.1 设计变量及灵敏度分析结果

修正导管架有限元模型所使用的初始设计变量见表3,为使修正的变量在现实条件中适用,表中给出了其变化范围。

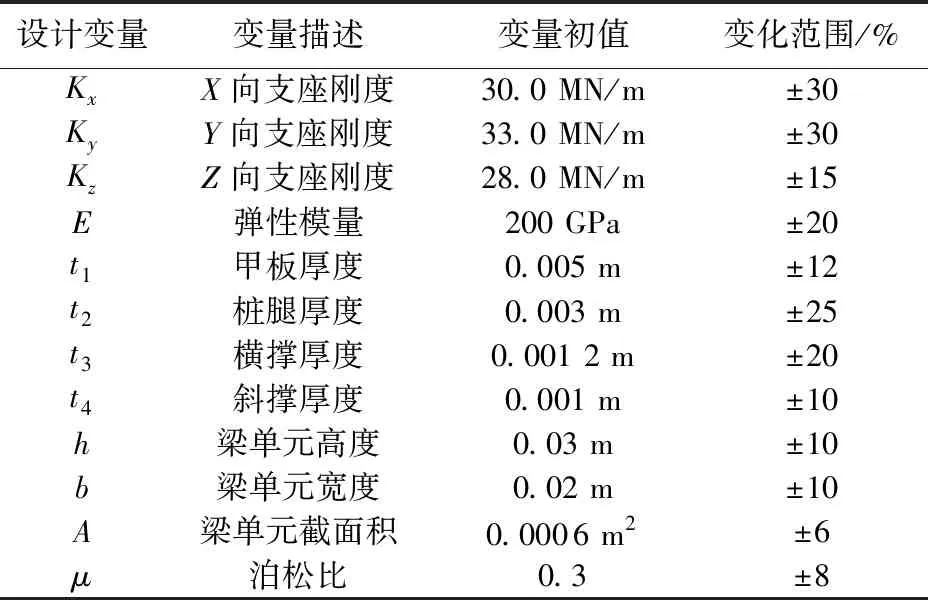
表3 选择的初始设计变量

由于不同阶次模态对同一参数的灵敏度一般不同,有些参数的灵敏度对低阶模态的影响很小,因此根据修正参数选取原则,需要根据有限元模型的前六阶模态分析各参数的灵敏度。对结构振动系统来讲,动力特性的灵敏度比率[12]可表示为结构参数对其特征参数(特征值和特征向量)的敏感程度,因此通过灵敏度比率分析可选出对结构整体动力特性影响大的参数,从而使得模型修正更加有效。灵敏度比率指各参数的灵敏度与其灵敏度区间的比值,由于灵敏度范围一定,因此各参数的灵敏度比率与灵敏度结果一致。

计算出弹簧刚度、弹性模量、密度、板厚、壁厚等修正参数前六阶模态灵敏度比率的平均值,绘制于图7。由图7可见,弹簧刚度的修正对导管架有限元模型的修正结果至关重要,其次是弹性模量和壁厚,而密度及板厚对修正结果的影响比较小。根据各参数的灵敏度比率所在区间,将其划分为Ⅰ、Ⅱ、Ⅲ级及大于Ⅲ级,相应的各级灵敏度比率分别为0.15、0.025、0.003、小于0.003(表4),其中分级的数值是通过各修正参数对减少模型误差的贡献来确定。在此,选择前三级(Ⅰ级、Ⅱ级、Ⅲ级)作为修正变量,即包括Kx、Ky、Kz、E、t1、t2、t3、t4、ρ、h、b和A。而泊松比对频率修正影响比率小于0.003,故剔除。

根据表4,对前三位的修正参数即弹簧刚度、弹性模量和壁厚进行修正。进一步,分别研究其对前六阶各阶模态的灵敏度比率的影响,结果见图8。由图8可知,弹簧刚度对第三阶模态的影响最小,而弹性模量和壁厚则对各阶模态的影响较均匀。

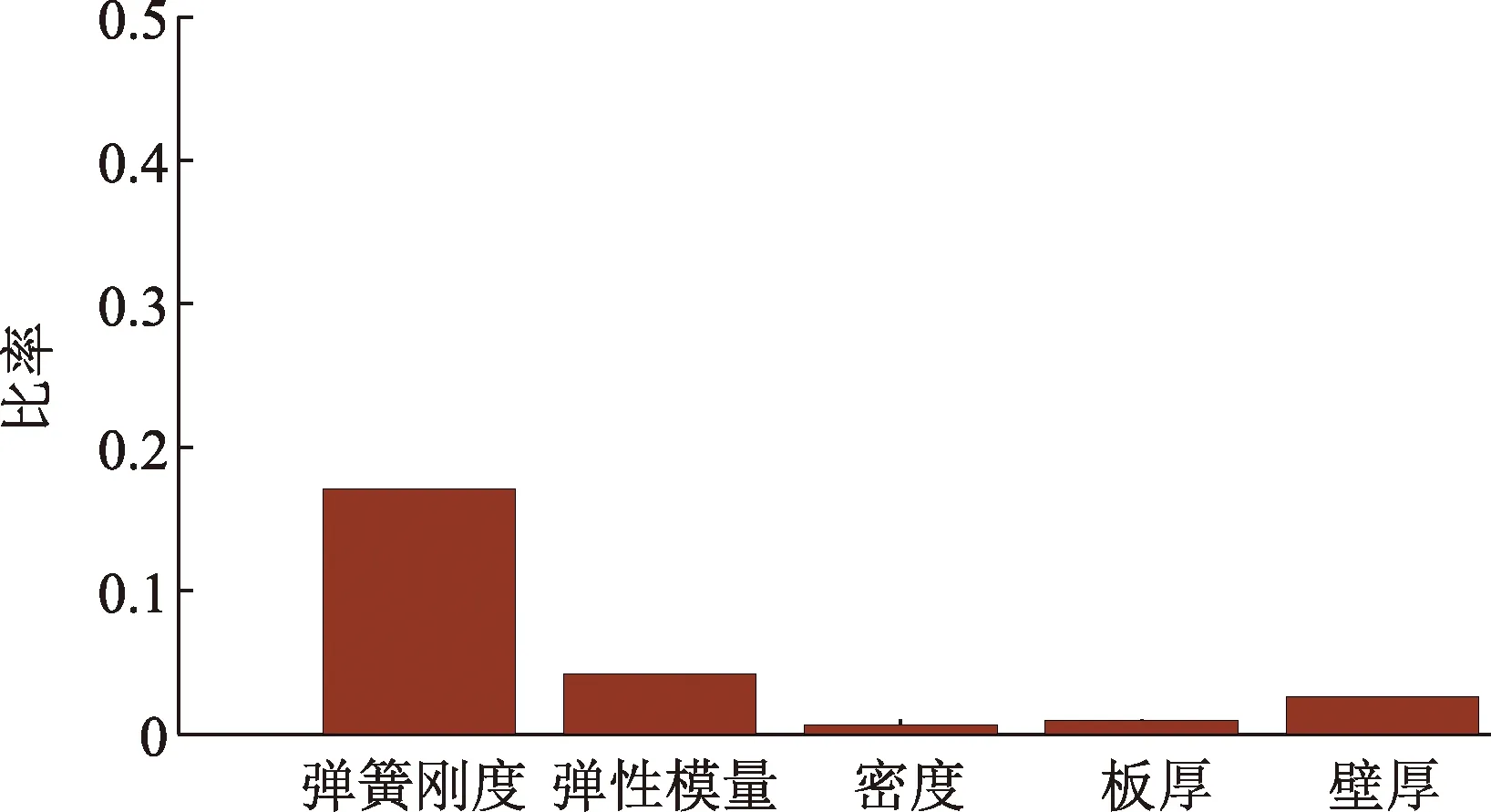
图7 各修正参数灵敏度比率平均值Fig.7 Mean sensitivity indices for each correction parameter

表4 灵敏度等级

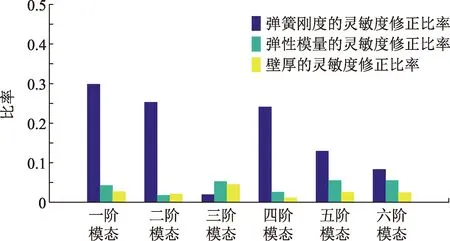
图8 弹簧刚度、弹性模量、壁厚的灵敏度分析Fig.8 Sensitivity analysis of spring stiffness,elastic modulus and tube thickness

4.2 基于灵敏度分析的有限元模型修正结果

采用试算法[22]对Ⅰ级、Ⅱ级、Ⅲ级设计参数进行修正。试算法是一种简单易行的方法,其基本思路是:首先判断修正参数的变化是否使结构有限元模型的频率更接近试验测得频率,从而决定修正参数的变化趋势;然后,在两个非常接近的小区域采用二分法对参数进行修正,并最终确定修正参数的数值。图9给出了试算法的修正过程,依次按照修正弹簧刚度、弹性模量、密度、板厚和壁厚的顺序进行试算。由图9(a)、(b)可见,当试算法进行到第5步后,有限元模型修正后计算的频率和试验结果非常接近,此时,点落在斜率为1的斜线上。

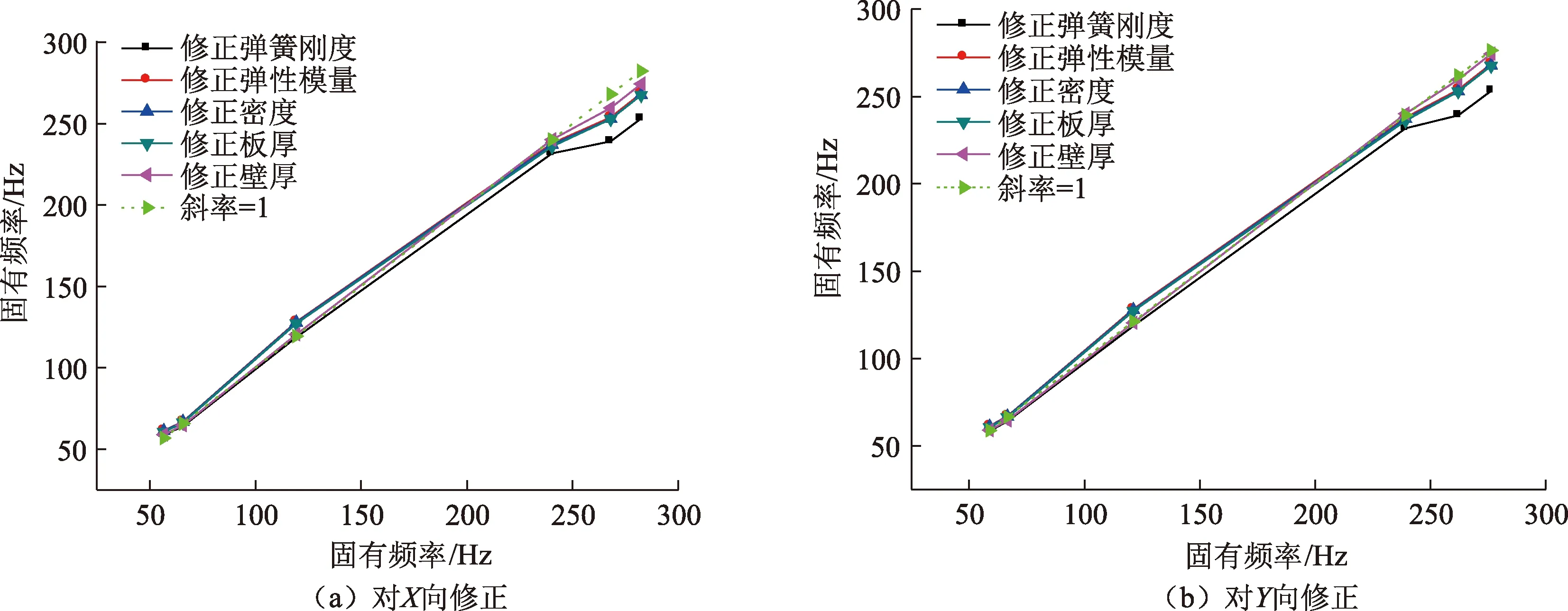
图9 试算法修正过程Fig.9 FE updating progress of trial method

图10给出了试算法的修正结果。由图10(a)可见,模型修正后的前六阶频率与试验频率非常接近;图10(b)进一步给出了各阶频率修正后的数值与试验数值之间的误差,可见,对于X向最大误差为3.92%,平均误差为2.11%;对于Y向最大误差为2.99%,平均误差为0.97%。由此可见,Y向敲击试验得到的频率与模型修正后的频率更接近。这些结果表明,有限元模型修正后,其固有频率与试验结果之间的最大误差为3.92%,这一数值小于5%,表明了试算法的有效性及可行性。

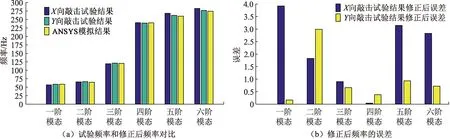
图10 试算法修正结果Fig.10 FE updating results of the trial method

4.3 基于优化设计的有限元模型修正结果

对海洋平台的有限元模型进行修正,进行了80次迭代步计算。计算中发现,优化程序在第4步收敛结束,最佳设计序列是第35步,此时的设计变量、状态变量和目标函数如表5所示。其中小括号里的数值表示试验测量得到的固有频率,频率误差是指ANSYS优化后的数值与Y向敲击试验数值之差。由表5可见,该优化程序得到的前六阶频率误差的平均值为2.78%,这表明优化分析法正确且可行。

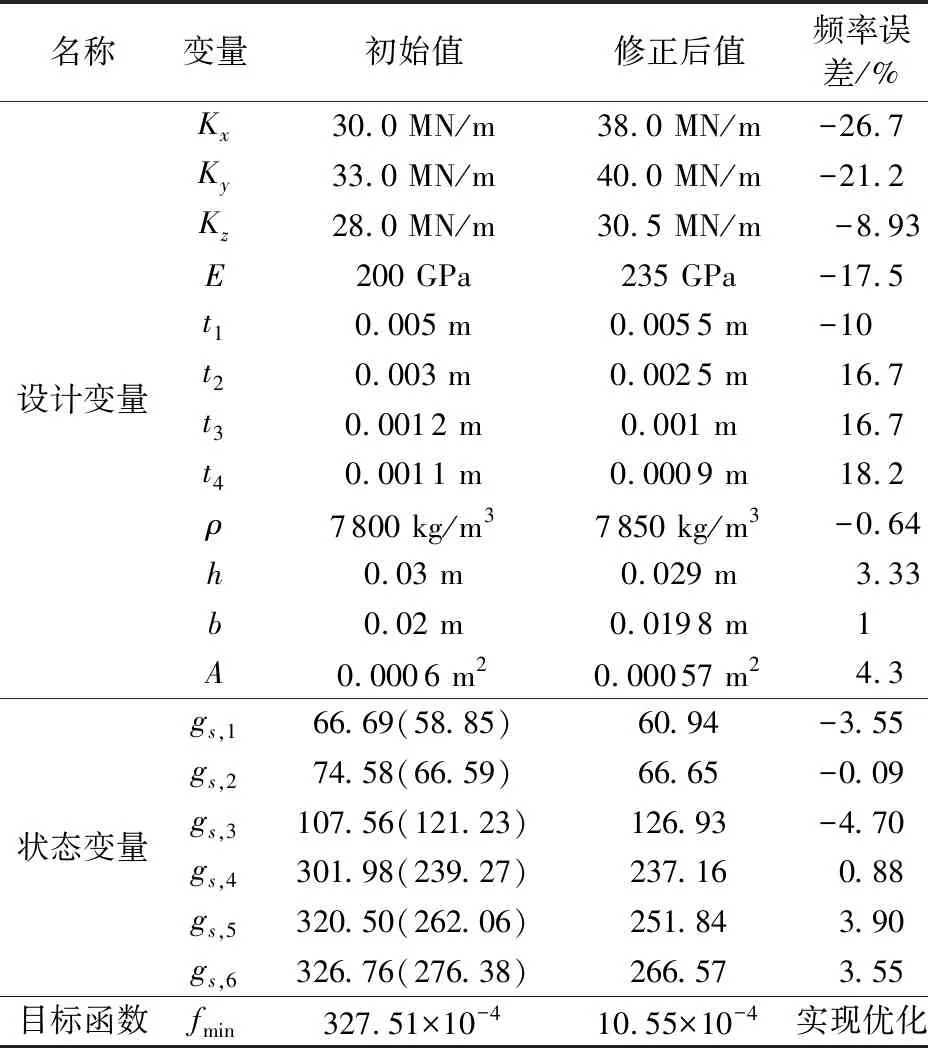
表5 设计变量、状态变量和目标函数Table 5 Design variables,state variables and objective functions

4.4 损伤导管架模型模态试验及有限元模型修正结果

对于服役多年的海洋平台结构,在长期恶劣的环境载荷作用下,结构容易产生如腐蚀、疲劳、构件断裂等各种形式的损伤,从而导致结构的性能与初始状态发生变化。因此,对于服役中后期的海洋平台,结构的损伤定位是损伤结构有限元修正的前提。

图11 损伤导管架试验模型Fig.11 Damaged jacket test model

采用图11所示的损伤导管架试验模型模拟构件断裂损伤,并设置了两处损伤位置。采用与前面相同的方法对该损伤导管架结构进行了模态试验,并进行了模态参数识别。同时建立相应未损伤状态的有限元模型(图12)用于模型的优化分析,图12中可见损伤单元的位置分别是11号和15号管单元。对该有限元模型进行模态计算,得到前六阶固有频率,并将试验结果及ANSYS计算结果列于表6。由表6可见,结构发生损伤后,结构的固有频率明显下降。因此,在基于有限元分析进行损伤结构的安全评估时,需要准确找出损伤部位,并据此对原始有限元模型进行修正。

从表6中可见,结构发生构件破坏后MAC值明显小于结构完好时的MAC值,尤其是第一阶振型的MAC值仅为0.33。这表明结构损伤后试验振型和ANSYS模拟振型的相关性大大降低。即结构损伤后,其初始有限元模型已无法反应出结构的真实动力特性。

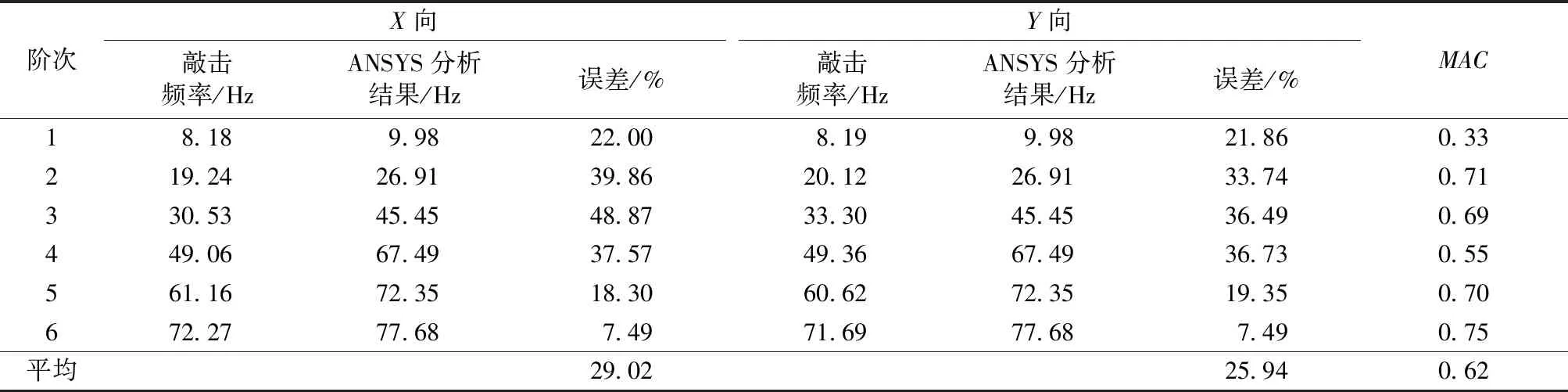
表6 前6阶频率的试验结果与有限元模拟结果及其相关性

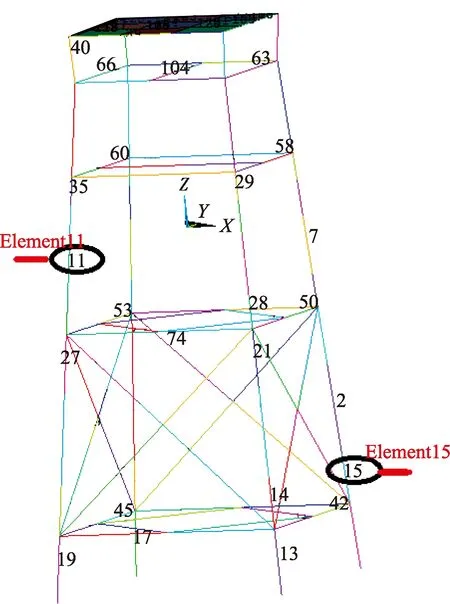
图12 待修正模型Fig.12 Model to be updated

为定位出该损伤平台结构发生构件断裂的位置,并进行有限元模型的修正,采用前面的优化方法进行优化分析。优化程序共迭代45次,在第4步收敛结束,最佳设计序列为第16步,此时的设计变量、状态变量和目标函数见表7。其中E1到E31分别表示导管架中各管单元的弹性模量,初始值均设置为200 GPa,优化后E11和E15的数值几乎降为零,表明11号和15号管单元即为损伤单元,这与实际导管架的损伤位置完全一致,表明优化准确可行。优化结束后,得到前六阶频率误差的平均值为4.79%,由此可以推断,损伤后导管架模型的频率误差稍微大于完整导管架模型的频率误差。

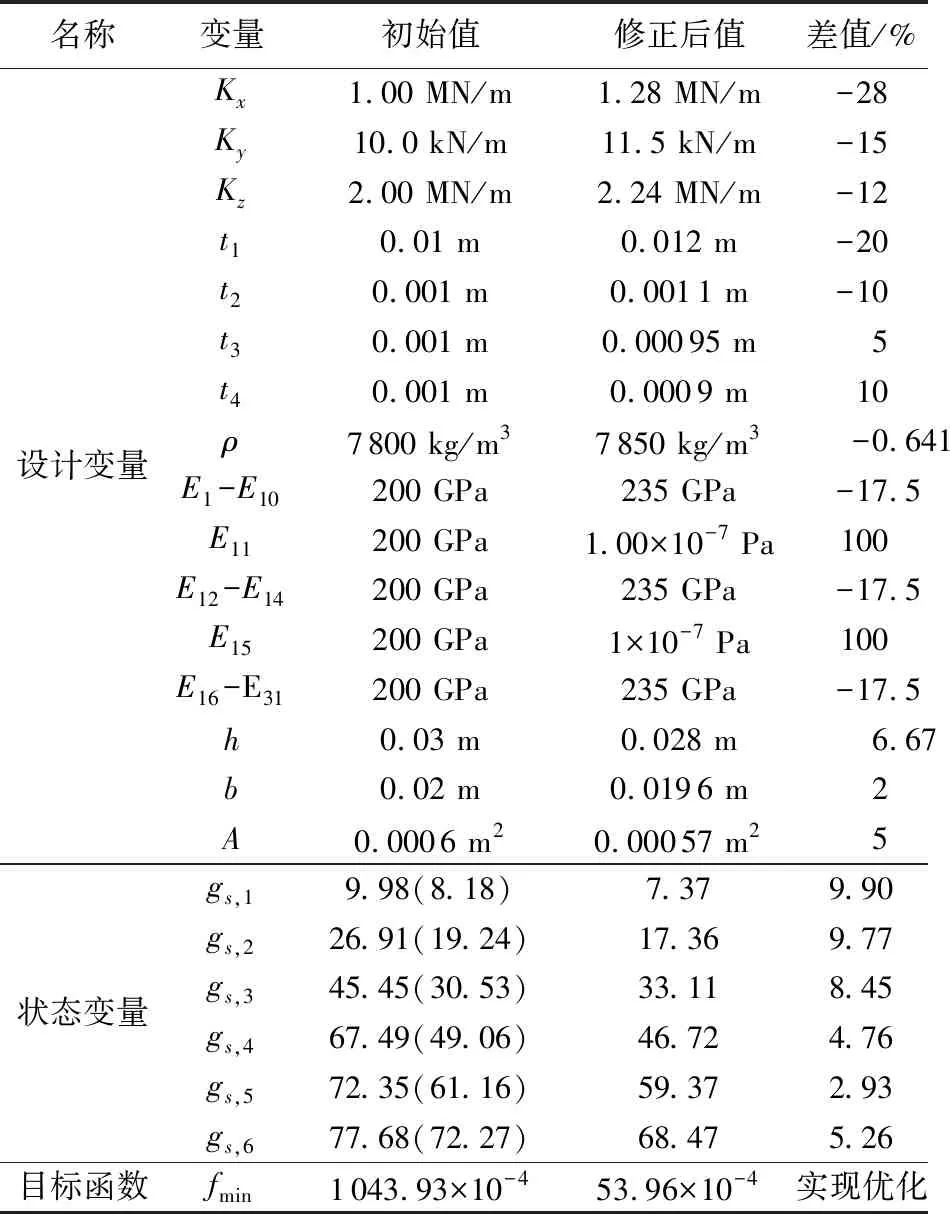
表7 设计变量、状态变量和目标函数

5 结 论

(1)利用模态置信准则MAC能够对缩尺模型模态试验数据和有限元模态计算数据的相关性进行有效评价。平台结构完整未损伤时,有限元模态计算值和试验测量值匹配良好;平台结构发生构件缺失的损伤时,试验振型与有限元模拟振型相关性比较差,MAC值明显降低,第一阶MAC值仅为0.334 304。

(2)有限元模型修正之前,可通过灵敏度分析识别灵敏性较大的参数,不仅可减少计算量也使得收敛速度大大提高。边界条件和弹性模量的敏感度很高,成为关键的待修正参数;修正后有限元计算的前六阶固有频率与试验结果相比,其平均误差从17.22%下降至2.78%,修正后的有限元模型更接近试验结构。

(3)对于含有构件缺失的损伤平台有限元模型的修正问题,可采用考虑边界条件的优化设计方法,本算例中设计参数共有42个,前六阶频率为状态变量,设置前六阶固有频率误差平方和的平均值为优化目标函数。根据该优化方法可准确定位出两个构件的损伤位置;修正后有限元模型的前六阶频率误差平均值由修正前的25.94%大幅下降为4.79%,这表明该方法的修正效果较好。