流沙沙漏视重变化现象的研究
刘思媛 伍 乐 周廷明 张 君 赵芸赫
(四川省成都市温江中学 四川 成都 611130) (北京师范大学物理学系 北京 100875;首都师范大学附属中学 北京 100048)
沙漏在流沙时,其视重会发生变化.这是因为系统中沙子在自由下落和冲击沙漏底盘时的超失重导致的.这样一个模型简单易于理解,是一个重要的教学模型[1~4].文献[5]通过计算沙漏系统质心的加速度随时间的变化模拟出了系统视重随时间变化的关系曲线,从定量的角度对这一现象做了很好的解释.由于沙漏几何形状较复杂,故得到的理论关系依赖于多个装置参数且过于复杂,不够直观.
本研究重点从定量的角度以最简单的沙漏模型对此现象进行理论与实验的研究,首先通过理论分析预测其视重变化及其影响因素,而后通过实验来印证理论解释以及探究影响视重变化的不同因素.最后,通过分析实验结果与理论分析中不一致的地方,进一步修正了理论模型.
1 理论分析
先假设一种理想的情况,如图1所示的装置,沙漏置于水平放置的秤盘上,初始时瓶中沙子质量为m,容器的质量为M,在t=0时,沙子开始释放并落到下面容器之中.先以初速度为零,不受其他外力干扰,且质量流率保持不变的理想化状况来进行分析.设过程中秤的读数为N,沙漏下面容器高为h,质量流率为λ,整个过程可分为如下几个阶段:
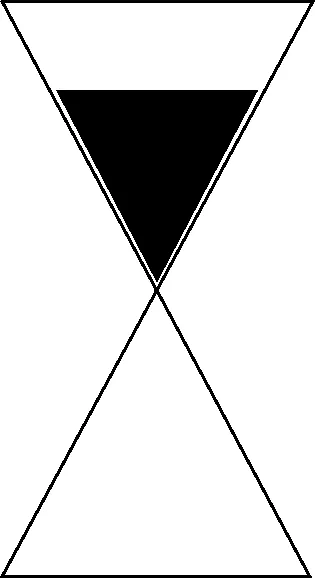
图1 沙漏装置示意图
(1)释放沙子之前,读数为沙子和容器的总重力.
(2)沙子下落到接触装置下底面之前的过程中,由于沙子在空中对装置没有作用力,故处于失重状态,示数不断减小,根据自由落体运动的规律,下落到底端时有
在沙子即将接触到底面,即t=t1时,其读数最小,有
(1)
(3)当沙子接触底面时,由动量定理,设冲力为F,则有
(F-Δmg)Δt=Δmv
(2)
由上式可得
且在Δt趋近于零时,Δm亦趋近于零,故
所以,在沙子接触底面到全部流出上端容器的过程中,由于沙子对底部的冲力作用,此时对于沙子的视重有
N=(m+M)g-m空g+F=
(m+M)g
(3)
其中m空为在空气中流动的沙子的质量,由式(3)可知,秤的读数变大为(m+M)g,恢复至初始重量.
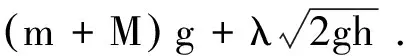
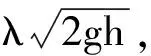
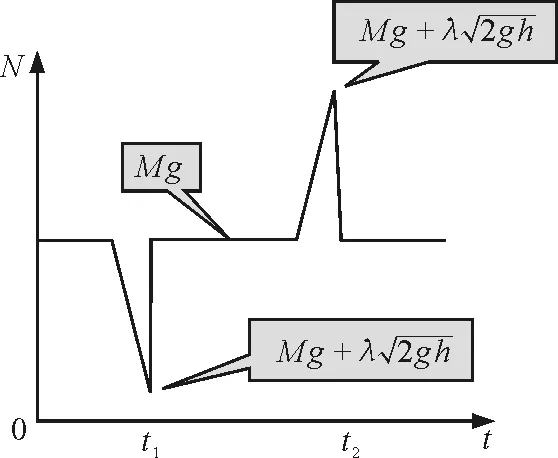
图2 流沙沙漏视重随时间变化的理论预测趋势图像
2 实验研究
2.1 实验设计与方法
2.1.1 实验装置的设计
实验装置如图3(a)所示,选取两个完全相同的瓶子A和B(市场上1.5 L的大饮料瓶),分别去头去尾作为实验容器,B用于释放沙子,A用于盛接沙子,为了能够实现改变瓶口高度,先在下容器A两侧固定住两长木条M和M′,为了保证装置的稳定性,木条需满足完全相等的条件.而后在上容器B的两侧,对称地固定一对相等的滑块N和N′.而对于整个装置由一根粗铁丝E与传感器相连,由电脑端接收数据并绘图.
关于沙子释放装置的设计,为了减小实验操作上的影响,我们利用栓紧的渔线将比瓶口稍大的塑料轻质圆片托起并堵住瓶口,然后通过蜡烛快速烧断渔线的方法来进行沙子的释放,如图3(b)所示.
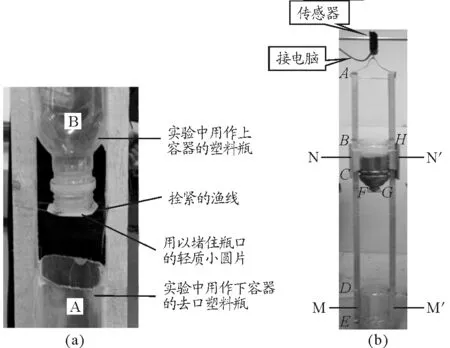
图3 实验装置实物图
2.1.2 实验装置相关参数及测量方法
对于装置中各种长度的测量,我们选用的是精确度为0.1 mm的刻度尺,实验装置相关参数如下:FG=2.86 cm;BC=17.32 cm;DE=18.96 cm;AE=126.50 cm;BH=8.59 cm;而对于沙子的直径,我们选用的不同目数的筛子进行筛选,接着通过目数的转化求得粒子直径,然后我们分别称量了空瓶和瓶中部分沙子的质量以及那部分沙子的体积,求得沙子密度,得到实验中所用沙子的直径和密度如下:d=0.6~0.7 mm;ρ=1.35 g/cm3.
对于沙子系统视重随时间的变化我们通过力学传感器进行测量,设置传感器精度为每秒钟取30个数据,且多次重复实验来进行分析,使结果具有普遍性.
2.2 实验结果
2.2.1 沙漏视重随时间的变化
图4所示为沙子下落初始高度h=30 cm的实验结果,可以看出,视重有一个先下降而后相对平稳,接着上升,最后再次趋于平稳的变化过程,与理论基本一致,但同时也有一定的差异,这将在后续讨论中提及.
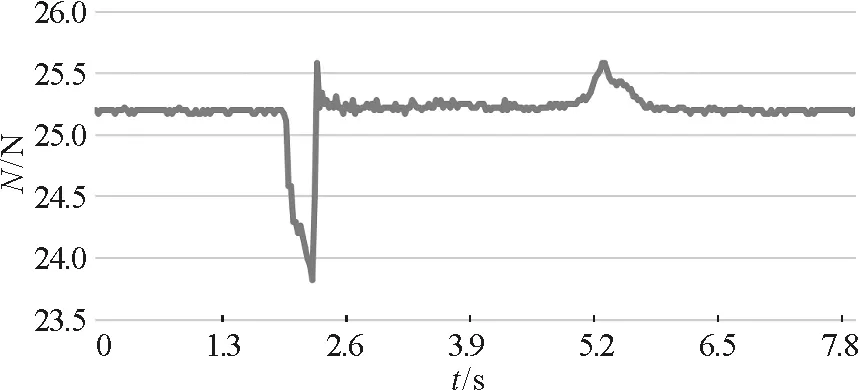
图4 h=30 cm时流沙沙漏视重随时间的变化
2.2.2 探究沙子质量对结果的影响
选用不同质量的沙子(400 g, 800 g, 1 200 g,1 500 g)来进行实验.实验结果如图5所示,可以看到,不同质量沙子的视重曲线中第二次峰出现的时间不同,这是因为不同质量的沙子稳定流出的时间长短不同.
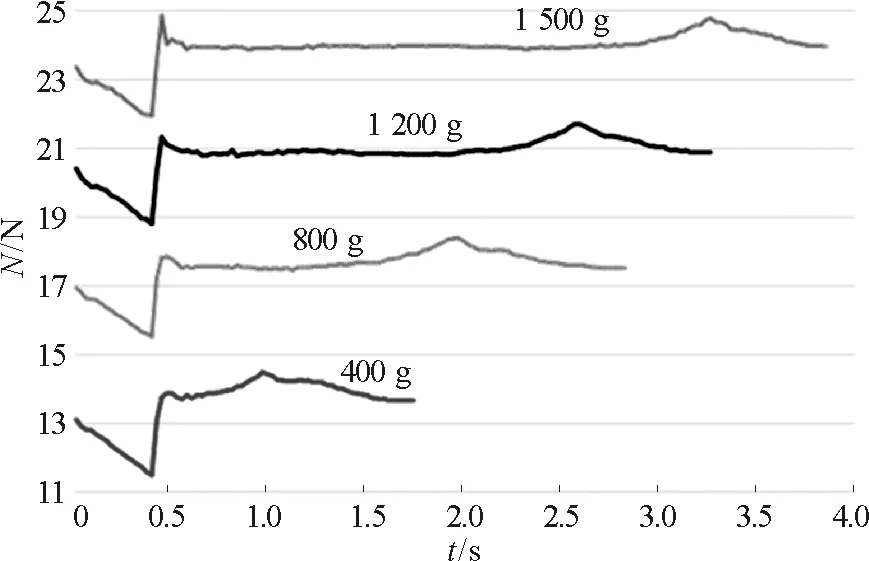
图5 不同质量的沙子对视重曲线的影响
为了便于分析和处理数据,我们将纵坐标设为系统视重与初始值的差值ΔN,得到图6,通过测量两个峰之间平稳段的长短大致相等,可以判断出沙子的下落规律基本相同,如图所示.
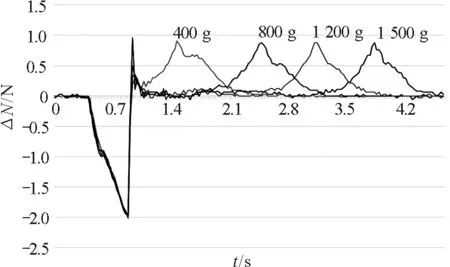
图6 重合后的图像
单独取出视重曲线中峰值部分(横坐标表示打点个数,纵坐标表示视重),得到图7,发现不同质量沙子得出的实验图像中的第二次峰值大小基本相同,符合理论分析,即峰值大小与质量无关.
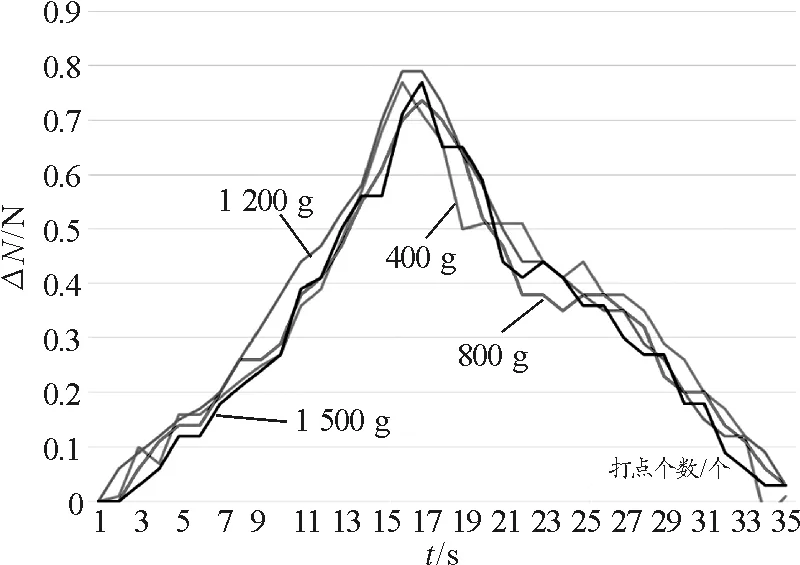
图7 不同质量的沙子视重曲线的峰值比较
2.2.3 探究沙子下落高度对结果的影响
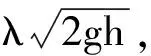

图8 沙子下落高度对视重变化曲线的影响
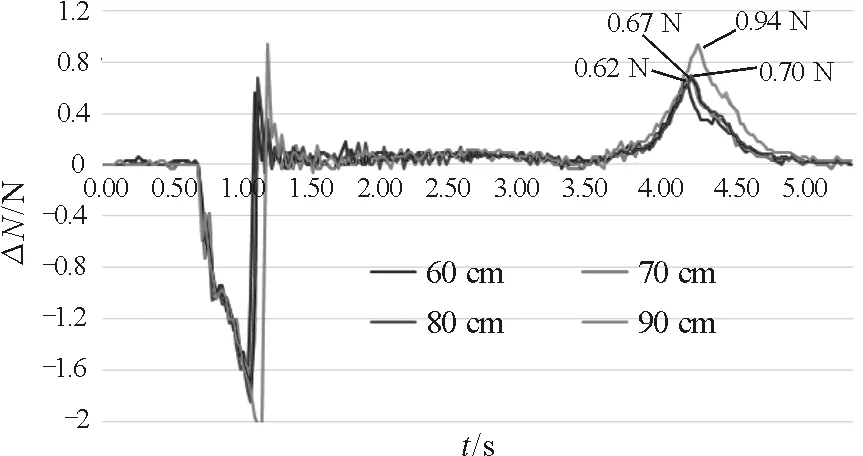
图9 沙子下落高度对视重变化曲线的影响

图10 峰值大小与h的拟合曲线
3 理论修正
通过对比实验与理论图像,如图11所示,可以发现,在沙子触碰底面后稳定下落时为超重状态,即此时的视重比沙漏系统的初始重量要大.这是由于沙子初始下落时有初速度的缘故,因此需要对理想化的理论模型进行修正.
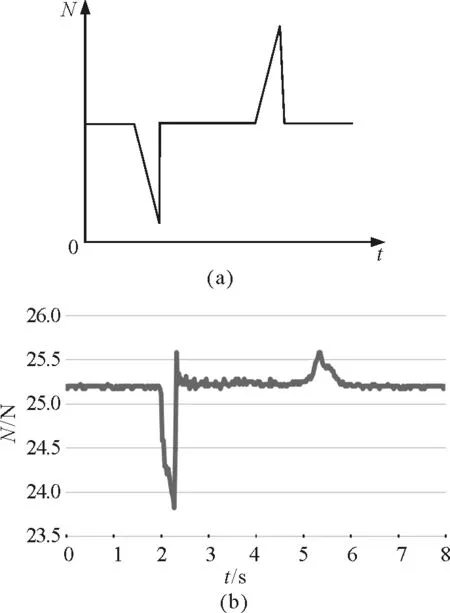
图11 实验与理论结果对比
考虑到沙子离开瓶口时有一定的初速度v0,且通过测量发现初速度较大.忽略其他外力的影响,同样假设质量变化率不变,设沙子从上部容器流出的出口面积为S0,则空气中的沙子质量、其运动情况及其与下部容器撞击的冲力有
m(t)=ρv0S0t
(4)
(5)
(6)
(F-Δmg)Δt=Δmv
(7)
将式(4)~(7)代入
N=Mg+F-m(t)
可得沙子稳定流出时的视重
比沙漏系统的初始重量要大.
修正后的理论模型示意图如图12所示.

图12 修正后的理论模型示意图
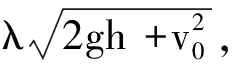
4 结论
本研究从定量的角度对沙漏在流沙过程中视重变化的现象进行了理论与实验的研究,理论研究将沙子运动过程分解为4个运动过程分别进行分析,通过简单的力学原理,解释了沙漏装置重量发生变化的原因,并给出了沙漏重量随时间变化的定量关系.
然后通过自制的实验装置设计实验对理论模型进行了实验验证.首先对视重曲线进行了定性验证,进而利用该装置验证了视重变化曲线中峰值大小与沙子下落高度成正相关,而与沙子的质量大小无关,实验结果与理论预测符合较好.对于实验结果与理论预测存在差异的部分,如沙子触碰底面后稳定下落时的视重比沙漏系统的初始重量要大,而理论预测为相等的差异,实验发现这与沙子流出上容器出口时的初速度有关,故考虑这一初速度的影响,本文又对理论模型进行了进一步修正,解释了实验结果与理论预测的差异.

