单摆实验的视频分析教学案例*
郭中华 郑隆举 朱振珲
(兰州城市学院电子与信息工程学院 甘肃 兰州 730070)
随着数字化技术在生活中各方面的广泛普及,如何将自然科学基础知识借助数字化技术应用于基础教学之中,提高学习者对信息的接受和分析能力,以响应社会对人才培养综合素质的要求,借助数字化实验平台建设,探索新型的物理实验教学模式,就值得尝试、研究和探索.本文借助Tracker软件分析单摆实验,进行数字化实验教学的尝试,为普通物理实验的教学提供一种有益的参考.
Tracker软件源于美国国家科学基金会(NSF)资助,始于2003年的开源物理项目(Open Source Physics Project,OPS),是其中很重要的一款开源软件之一.该软件主要功能是视频分析和建模,它能精确地捕获视频中质点的位移时间数据,并具有简洁高效的数据分析功能,建模模拟,可应用于运动学、动力学及光谱分析等的教学与研究[1].
单摆实验是普通物理实验(力学部分)中最基础、最重要的一个实验,在生活中,常见的秋千、钟摆等实物中都可以抽象出这种物理模型.传统的力学实验中,单摆实验基本有3点要求:
(1)利用单摆测定当地的重力加速度;
(2)验证单摆周期与摆长的关系;
(3)观察单摆周期随摆角的变化情况.
但在传统实验中,实验者不能直观地观察到摆球做简谐振动的运动规律,而且单摆的周期不易测准,摆长、摆角对单摆周期的影响也不能及时得到验证,影响实验效果.力学实验是物理学专业学生首先接触到的专业实验,但是低年级学生往往专业知识储备较少,计算机基础应用能力不强,编程语言能力差,借助Tracker软件来分析单摆实验,不仅可以直观地得到简谐振动的运动规律,测量相关物理量,还可借助其数据拟合功能,进一步分析实验中涉及到的物理现象规律.在较短的时间内,经过指导及自学练习,学生们就可以了解到物理建模、研究分析及计算模拟的整个研究型学习的过程,这对于科研能力的训练是十分有益的.
1 单摆实验
一个一端悬挂、质量忽略不计的轻绳(长为L)连接一个重物(质量为m),在摆角θ<5°下的无阻尼平面摆动过程,可视为单摆系统.取重物为小球,直径为d,对其受力分析,如图1所示.建立自然坐标系,在切向由运动微分方程
进一步整理可得
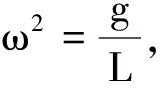
(1)
这是典型的简谐振动运动方程.从而可得到单摆的周期为
(2)
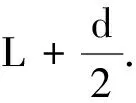
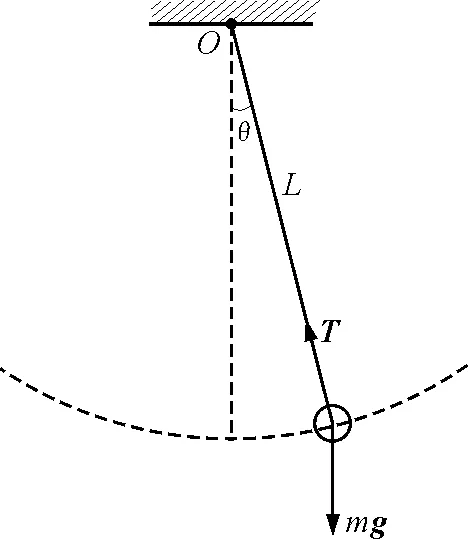
图1 系统示意图
从式(2)中进一步得到图1 单摆系统示意图
(3)
可见单摆系统周期平方和摆长应为线性关系,依据此线性关系,通过计算斜率的办法,亦可求得重力加速度.
当系统摆角θ>5°时,需要求解非线性运动微分方程
(4)
一般情形下,很难求解结果.用积分的方法,可求出含有第一类椭圆积分的单摆周期公式[2]
(5)
其中θ0表示系统的最大摆角,式(5)适用于任意摆角的情形,应用时查椭圆积分表可得精确振动周期.
为了简化计算,将式(4)中的sinθ做级数展开并利用三角变换,可得到θ≤90°运动单摆的近似周期计算公式
(6)
与椭圆积分计算结果的式(5)相比较,式(6)的精确度相当高[3].
2 Tracker软件对实验的分析
在实验前,给学生讲解软件的基本使用方法和实验视频的录制过程.对反映物体运动的实验片段进行录制时,为了保证后期摆球容易识别,通常实验背景与摆球的颜色二者相差要大.由于Tracker处理的是可供度量的时空坐标和尺度,为了方便起见,通常将物体位置的起点与运动开始的时间点作为时空原点.
2.1 简谐振动的运动规律
Tracker会以首次标记物体的形状为模板,在物体运动的过程中自动搜索匹配与模板相同的物体,这样就得到该物体许多连续的时空坐标,记录在窗口的表格中,同时还会绘制出质点的位移-时间以及速度-时间图像、加速度-时间图像.在摆角θ<5°条件下,分析录制好的单摆运动视频,在程序自动追踪摆球位置的同时,可在图像窗口同步观察其运动学特征.得到摆球的角位移-时间、角速度-时间以及角加速度-时间的变化规律如图2~4所示.
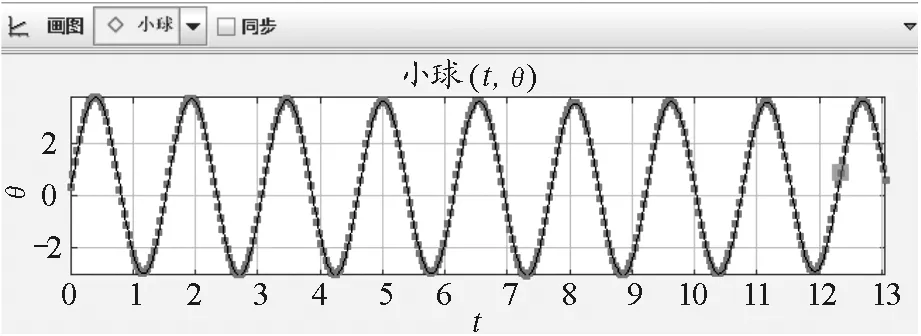
图2 摆球角位移-时间变化关系
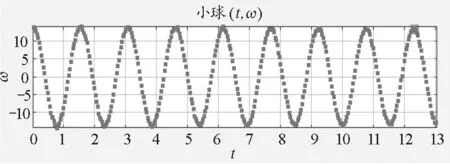
图3 摆球角速度-时间变化关系
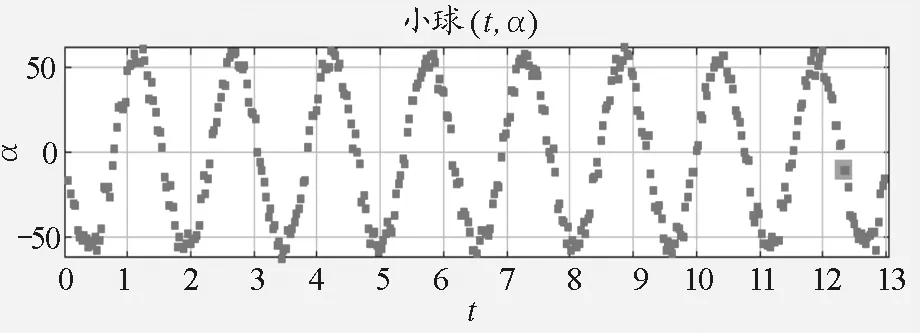
图4 摆球角加速度-时间变化关系
从图2~4可以看到,摆球的角位移-时间、角速度-时间、角加速度-时间均为余弦函数规律,当小球处于平衡位置处,角速度最大、角加速度最小;而在最大位移处,角速度最小、角加速度为最大.由于视频分析中追踪的是摆球的位置,据此数据得到速度,进一步得到加速度,因而数据有传递误差,导致角加速度随时间的变化曲线不够光滑.但是整体上,摆球的运动特征仍然符合简谐振动的规律,在实验中可以实时、直观地得到简谐振动的运动学图像.
软件的数据窗口中可直接读出摆球振动的时间值.一般在实验中,利用30~50个周期的时间值计算单摆的周期,由于视频分析中是针对每帧画面去定位摆球的位置并计算时间,因而测量数据准确度高.
在摆角θ=3.3°,L=58.10 cm条件下,得到单摆周期T=1.530 s.利用式(2),可计算得到本地的重力加速度数值g=9.788 4 m/s2.实验室所在地区重力加速度的理论值g=9.792 6 m/s2,则百分比误差Δg=0.042%,可见在实验规范操作,视频录制准确的情形下,所得结果的精确度是较高的.
2.2 验证单摆周期与摆长的关系
分析相同摆角、不同摆长情形下的单摆运动,利用软件分析拍摄好的视频文件,整理得到不同摆长下的周期数据,如表1所示.
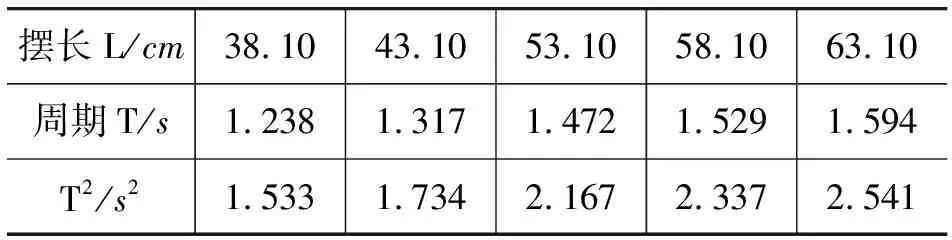
表1 不同摆长下的周期数据列表
将数据导入Tracker,在数据分析窗口中研究T2-L的关系,如图5所示.
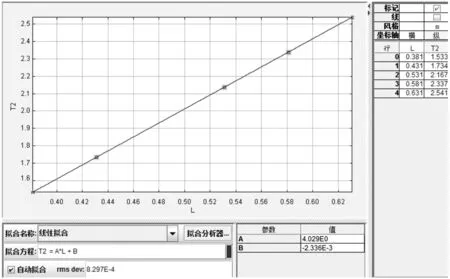
图5 小球周期平方与摆长的关系
从图5中可以看出,摆球周期的平方与摆长成线性关系,摆线长度越大,则单摆周期也越大.利用Tracker软件的数据分析工具,对所得数据进行线性拟合,在参数窗口中可直接得到相关拟合参数.图5的结果中,曲线的斜率
从而计算得到当地的重力加速度g=9.798 6 m/s2,则百分比误差Δg=0.061%,实验结果精确.
2.3 分析摆角对单摆周期的影响
当摆角θ>5°时,单摆的运动已经不是简谐振动了,但是在无阻尼情形下,仍然是周期性运动,其运动周期和摆角的关系可以利用实验结果进行分析.实验中,摆长取为L=52.10 cm,对不同摆角下的单摆运动进行视频分析,读取其对应的周期数据如表2所示.

表2 摆角变化情形下周期实测数据
将数据导入Tracker中,分析摆球相对周期随摆角的变化规律,结果如图6所示.
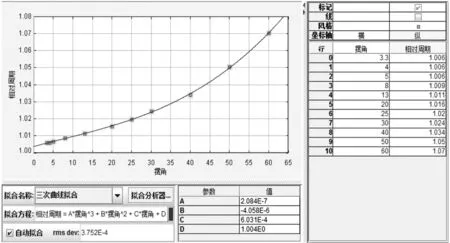
图6 大角度单摆相对周期随摆角的变化规律
3 总结
在教学中利用视频软件分析单摆实验,减少了实验中的系统误差及读数误差,可以精确记录摆球的运动轨迹,直观地得到简谐振动的运动规律,提高了实验者的兴趣和热情,有利于基本理论的理解和掌握.利用其数据拟合功能,进一步分析运动特征,并测量当地的重力加速度,简便、快捷,能帮助实验者更好地理解单摆的运动规律及应用.对于低年级学生来说,通过实验的研究分析与物理模型的建立过程,结合数值计算方法的简单数据处理,是一种有益的科研训练过程.将实验资料整理存档,可作为基础物理数值模拟实验的一部分,在经典物理教学中实现物理实验的数字化分析,开展新颖的物理实验教学模式,是物理实验教学改革的一种有效途径,值得探索.

