温度场作用下有初始间隙的补强圈接触特性和应力分析

(惠生工程(中国)有限公司，上海 201210)

0 引言

压力容器壳体上开孔接管的存在，一方面削弱了壳体本身的承载能力；另一方面在接管与壳体连接处因结构不连续性产生较大的附加局部高应力，极大地削减了此区域的强度而成为最薄弱的环节[1-5]。补强圈作为一种经济有效的补强措施得到广泛应用，可用来降低容器局部薄弱区域的高应力，进而提高容器的整体强度和承载能力。多年来，压力容器应力分析一直沿用经典的薄壳理论，在对开孔补强区域进行分析和设计时，将其分为壳体、接管和补强圈三部分，并通过在连接处建立变形协调及力的平衡方程求解此处的位移和应力，但前提是假设补强圈与壳体之间没有相对位移和转动；也未考虑相互间存在的接触行为[6]。然而在补强圈的实际制造和安装过程中不可避免会存在一定的间隙，载荷作用下的补强圈与壳体间会存在一定的相对位移和转动，进而导致与时间历程相关的接触位置和接触压力的变化，同时温度场的存在会使得总体或局部不连续区产生较大的温差应力和峰值应力，这必然会对开孔接管区及焊缝区的总应力分布产生一定的影响[7]。本文基于有限元法，采用特殊接触单元模拟补强圈与壳体之间的接触行为，对有初始间隙的补强圈结构在内压及与温度场耦合作用下的接触特性(接触压力和接触位置)和总应力变化规律进行分析，以期能够为工程实际提供一定的理论参考和设计依据[8]。

1 补强圈结构有限元模型和参数设置

本文以压力容器常用的焊接补强圈结构建立有限元模型，补强圈外径为接管外径的2倍，厚度与壳体厚度相同，壳体段和接管段长度既满足补强有效宽度和长度的要求、又远大于局部薄膜应力的衰减长度。在实际制造和安装过程中，由于误差造成的初始间隙的随机性难以定量，为便于分析，将初始间隙模型简化，补强圈外边缘与壳体间隙为0.18 mm，至补强圈内边缘时，与壳体间隙增大至0.2 mm(见图1)。由于分析模型中几何结构、材料、载荷和边界条件具有对称性，故采用1/4模型施加对称边界条件既能保证计算精度、又可缩短计算时间。补强圈和壳体之间定义摩擦接触，摩擦系数取0.3，实体单元选择Solid 185单元，接触单元选择特定的Conta 174单元和Targe 170单元。针对大变形非线性接触分析，采用减缩积分法和增广拉格朗日算法可保证较好的收敛性和计算精度[9-10]。基于上述模型、参数设置及第三强度理论的应力分类法，对此补强圈结构在内压单独作用(工况1)、内压和温度场耦合作用(工况2)两种工况下的接触特性、总应力及各类应力分布规律进行分析和理论探讨。

(a) (b)

图1 补强圈结构有限元模型

2 内压作用下补强圈接触特性和应力分析

2.1 补强圈与壳体之间接触特性分析

补强圈和壳体、接管结构在内压作用下应满足变形协调以达到结构的稳定，当变形较大使得补强圈与壳体之间的缝隙闭合而产生接触时，补强圈与壳体之间则会产生一定的接触压力。图2示出补强圈与壳体相对位置，图3示出接触压力随时间历程加载(内压逐渐增加大)的变化情况。

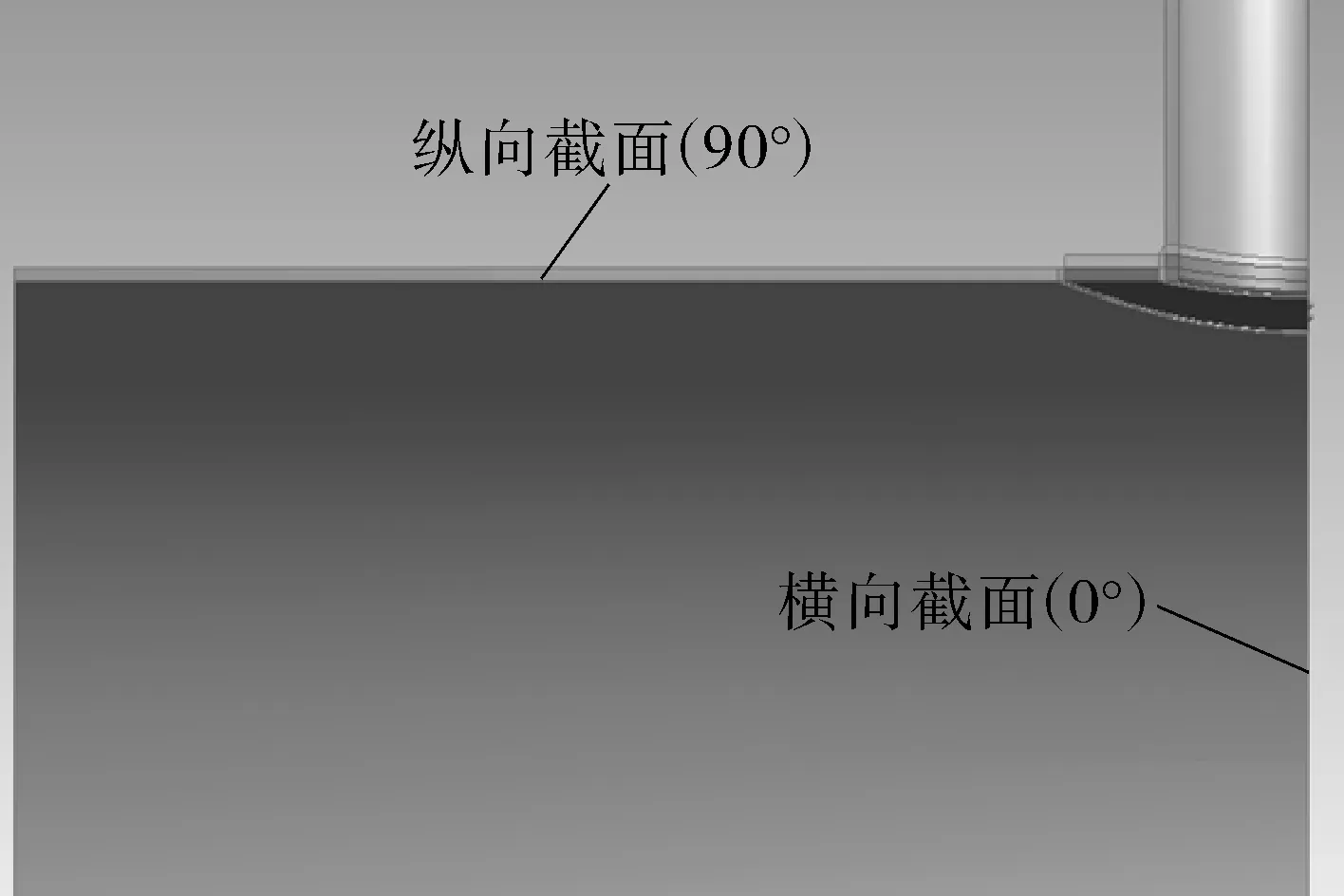
图2 补强圈与壳体相对位置示意

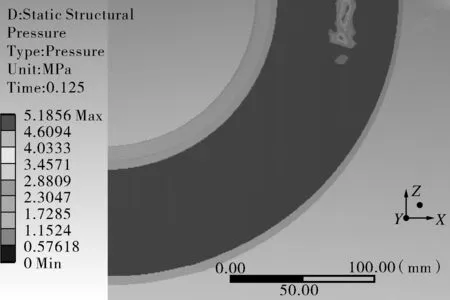
(a)t=0.062 5 s,p=2 MPa

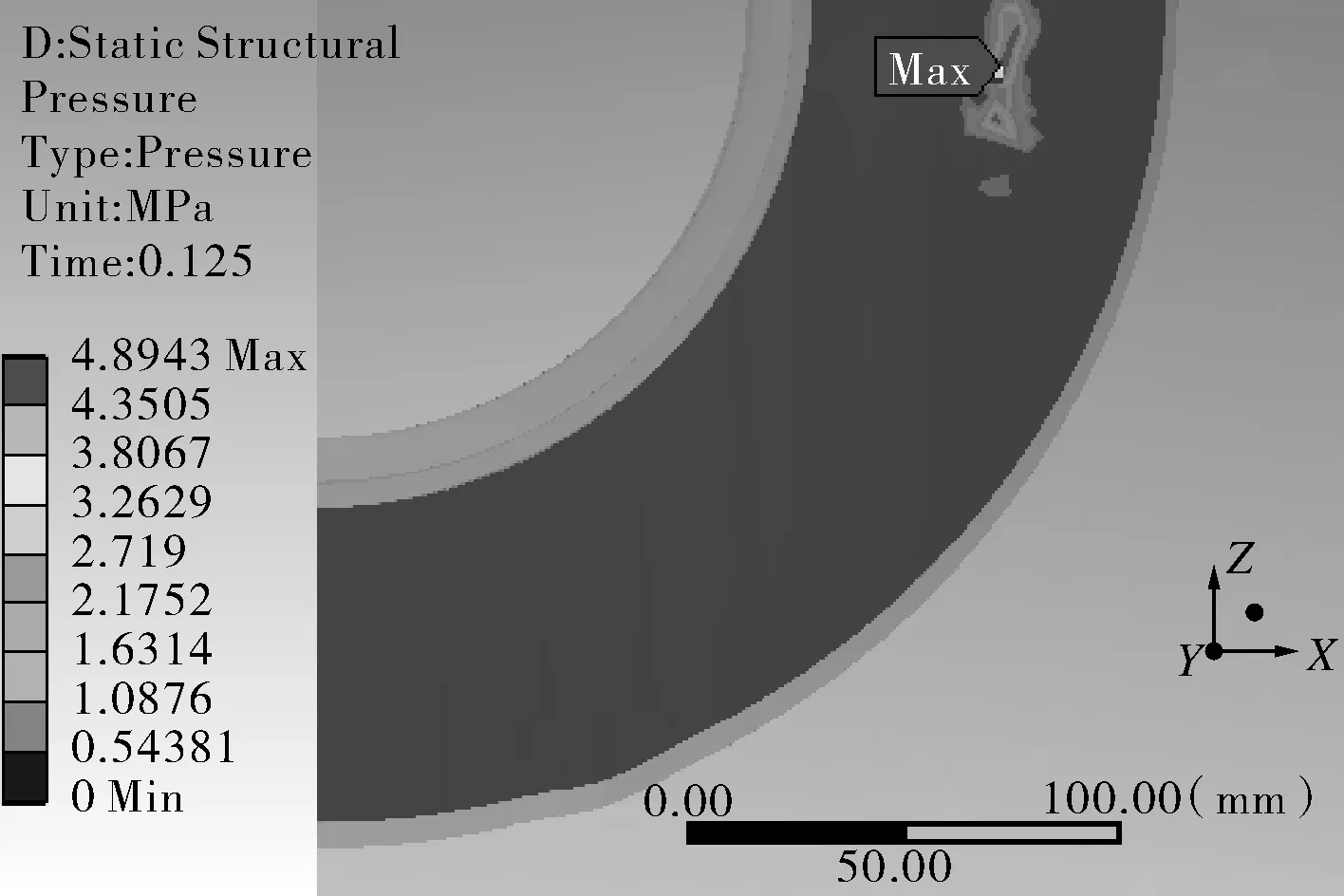
(b)t=0.125 s,p=4 MPa

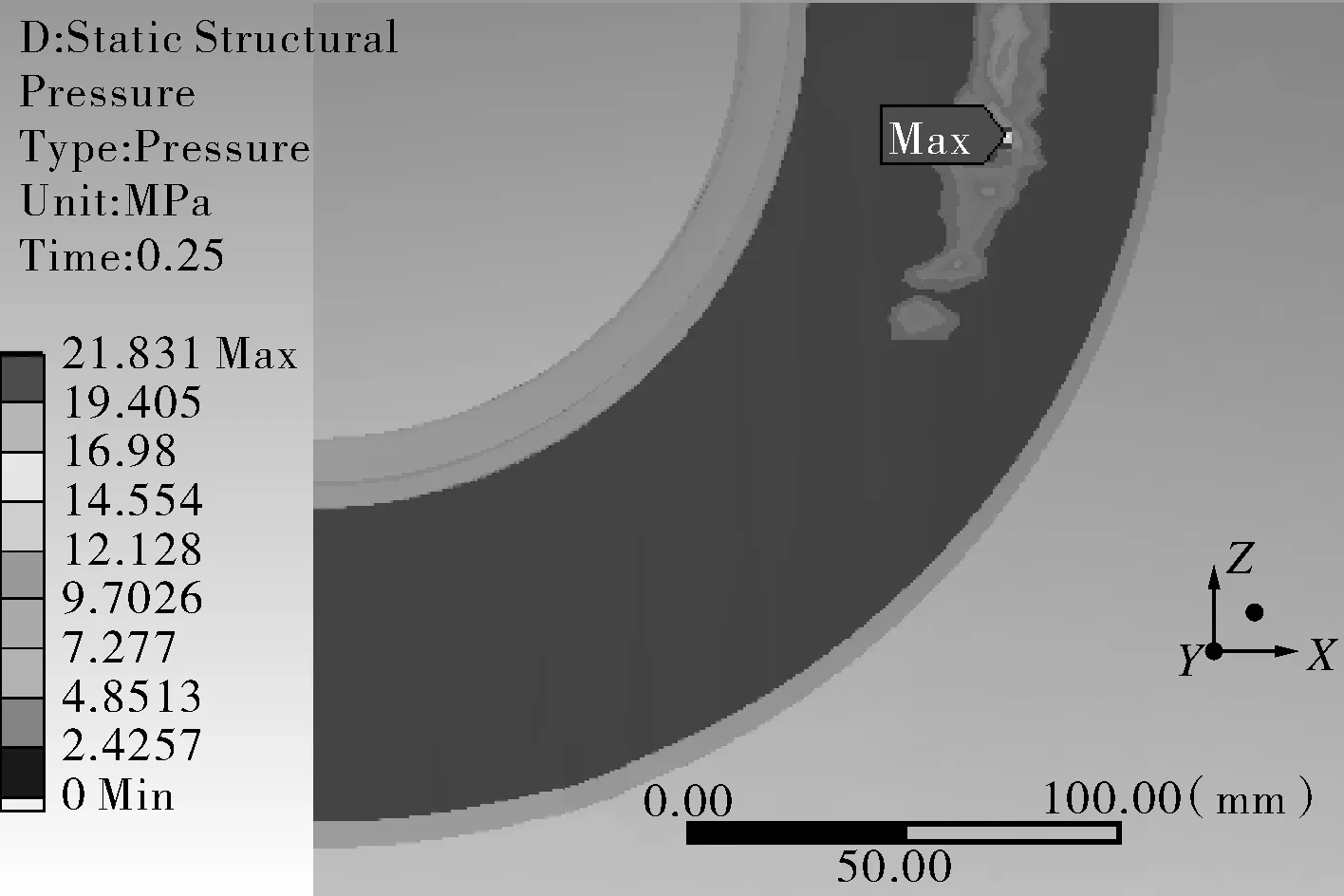
(c)t=0.25 s,p=8 MPa

图2还定义了横向截面(0°)和纵向截面(90°)位置，以方便后续表述。由图3分析可知，因有初始间隙的存在，在加载时间较短时(即内压较小时)，补强圈与壳体之间并无接触而无接触压力的产生，但随按时间历程加载内压的增大，壳体开始产生一定的变形并逐渐增大导致两者之间间隙闭合达到面接触，壳体的进一步变形则会受到补强圈的限制，因而两者之间开始产生一定的接触压力，且接触压力随着内压的增大而逐渐增大。另外可以看出，补强圈与壳体接触位置和接触压力最开始出现在横向截面内外焊缝中间位置处，之后随内压的增大逐渐开始向纵向截面过渡，同时在横向截面附近区域接触位置逐渐向内外焊缝位置处过渡，在内压达到一定值时，补强圈与壳体沿环向方向全部达到接触且在横向截面附近区域的接触压力和接触面积始终大于纵向截面位置区域[11](如图3(f)所示)。

2.2 补强圈与壳体、接管组合结构应力分析

容器壳体加上补强圈后相当于又增加了一组非连续性结构，同时上述分析已证实在内压达到一定值时补强圈与壳体之间接触压力的存在，且补强圈和壳体之间产生的接触压力必然会在补强圈与壳体焊缝处产生额外的应力并导致总应力的重新分布，使得焊缝处成为除接管与壳体相贯区以外新增的局部高应力区域，因而分析这些局部高应力区域的总应力及各类应力分布趋势对于正确认识补强圈结构具有一定的理论意义。

有限元计算结果表明，在不同内压作用下，最大总应力始终出现在接管根部内表面位置，补强圈与壳体外焊缝位置也是一个局部高应力区，而内焊缝位置应力值较小，无需进一步分析(见图4(a)～(c))。限于篇幅，以t=0.062 5 s,p=2 MPa时的计算结果进行应力分析探讨，由图4(b)，(c)可看出,接管根部内表面的最大总应力值出现在纵向截面区域(90°),且随着向横向截面区域(0°)的过渡逐渐减小至最小值；而在补强圈与壳体外焊缝位置，总应力变化趋势则恰恰相反。由图4(d)分析可知,在横向截面区域(0°)，薄膜+弯曲应力在外焊缝位置最大，从外焊缝位置至接管根部内表面位置呈线性减小趋势，总应力在外焊缝位置较大，至接管根部内表面位置则急剧减小，原因在于0°截面区域位移变形最大导致接触压力最大，外焊缝位置在接触压力的作用下即产生额外的一次+二次应力，同时，由于局部结构的不连续性且为满足变形协调而产生了很大的峰值应力，而接管根部内表面因为圆角的存在则大大降低了峰值应力；在纵向截面区域(90°)，薄膜+弯曲应力则在接管根部内表面位置最大，至外焊缝位置则呈线性减小的趋势，与0°截面区域正好相反，而峰值应力在外焊缝位置(变形较小无接触压力)和接管根部内表面位置均较小。综上所述，对于补强圈及壳体、接管结构，接触压力是真实存在的，且会显著引起外焊缝位置的局部高应力，导致存在两个高应力区域：横向截面区域的外焊缝位置(主要由较大的峰值应力造成)和纵向截面区域的接管根部内表面位置(主要由较大的薄膜+弯曲应力造成)。

(a)总应力分布云图

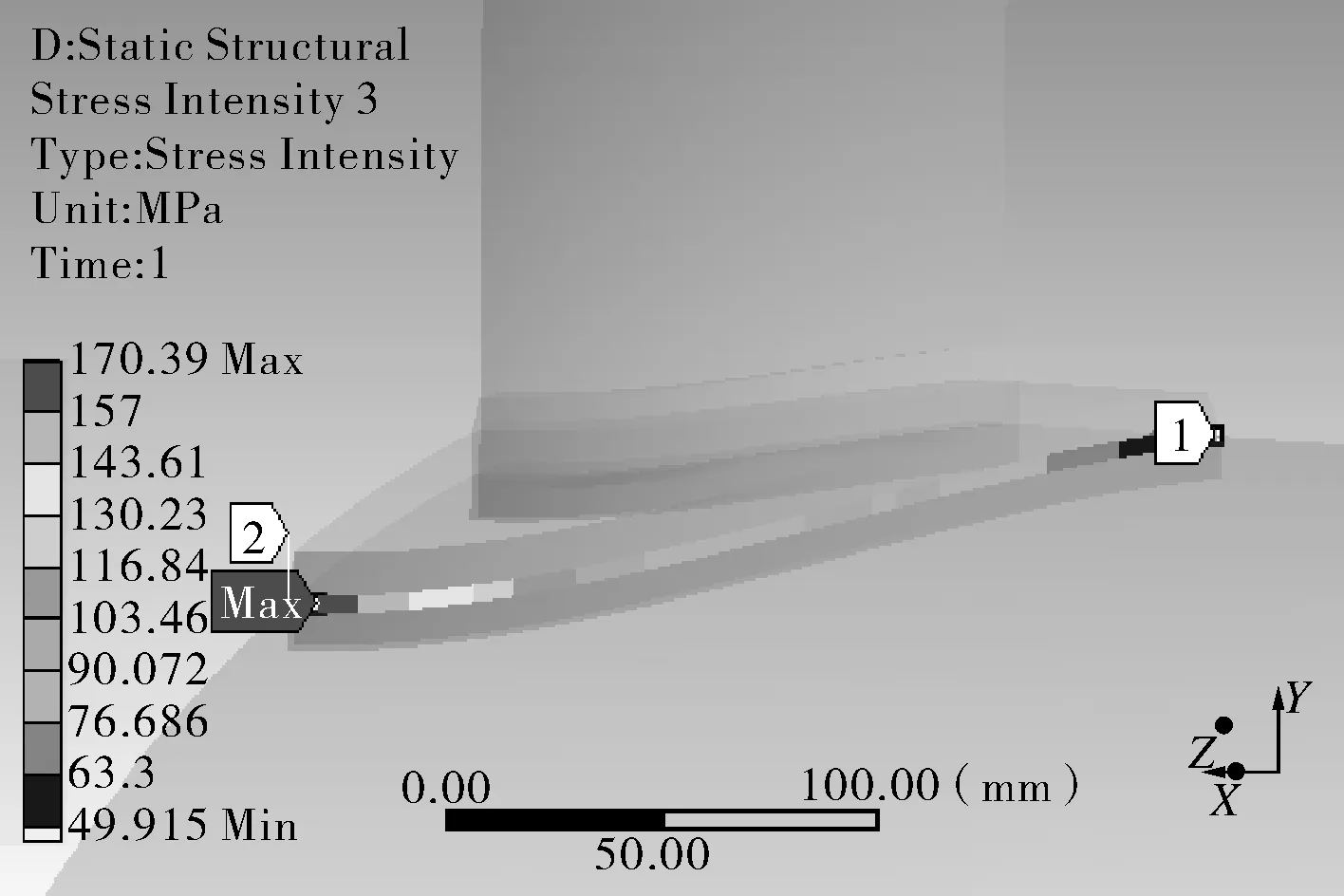
(c)补强圈与壳体外焊缝区域总应力分布趋势

(b)接管根部内表面总应力分布趋势

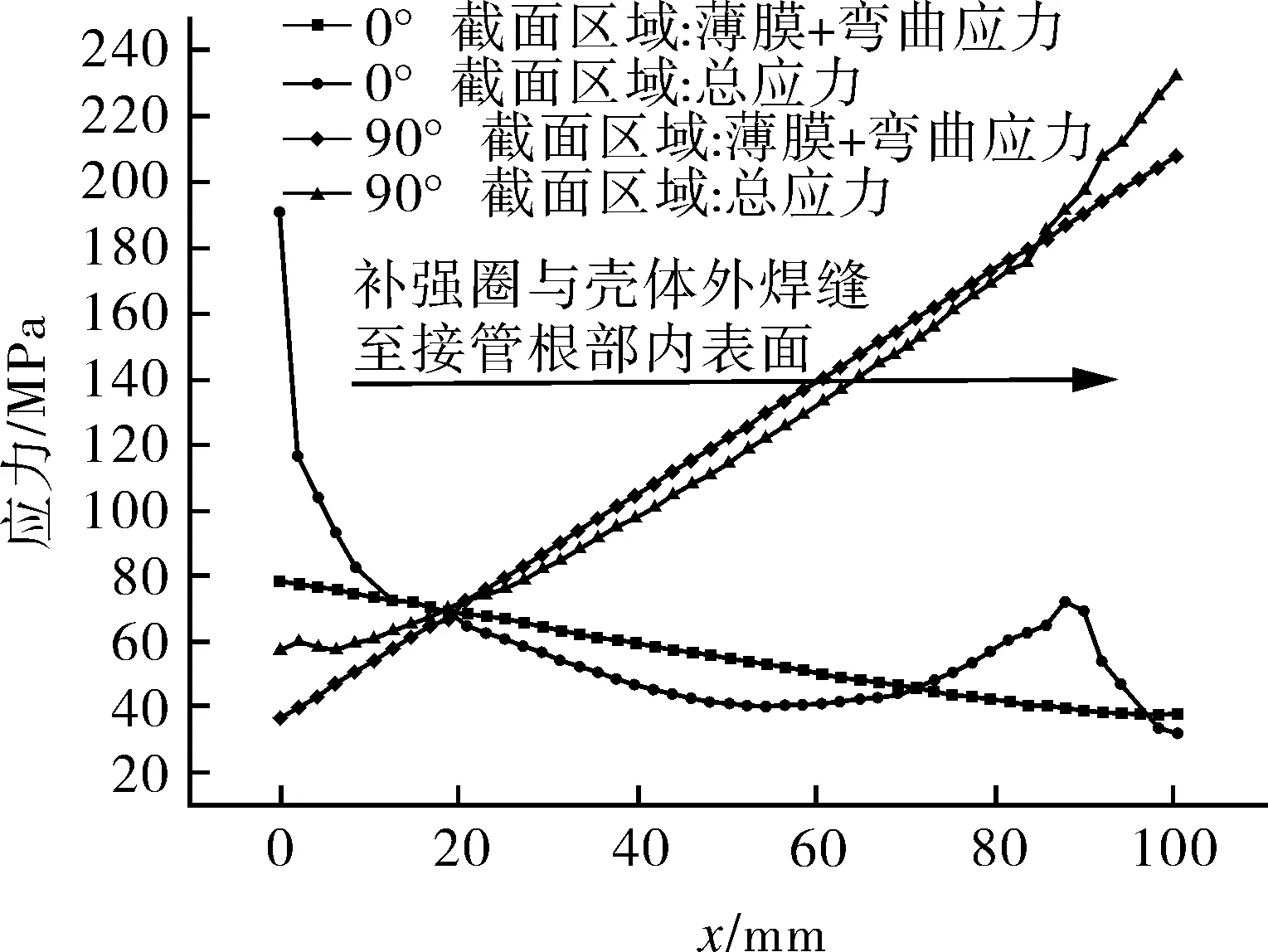
(d)0°和90°区域外焊缝至接管根部内表面各类应力变化曲线

图4 补强圈与壳体、接管组合结构各类应力分布趋势图

3 内压和温度场耦合作用下补强圈接触特性和应力分析

压力容器的实际运行都是在一定操作压力和操作温度下进行的，壳体内壁与有一定温度的介质接触，外壁则与保温层或空气接触。根据传热学原理，在热对流或热传导的作用下，壳体必然会存在一定的温差，故同时考虑内压和温度场耦合作用下补强圈结构的接触特性和总应力及各类应力分布情况更具实际意义[12]。

3.1 补强圈与壳体之间接触特性分析

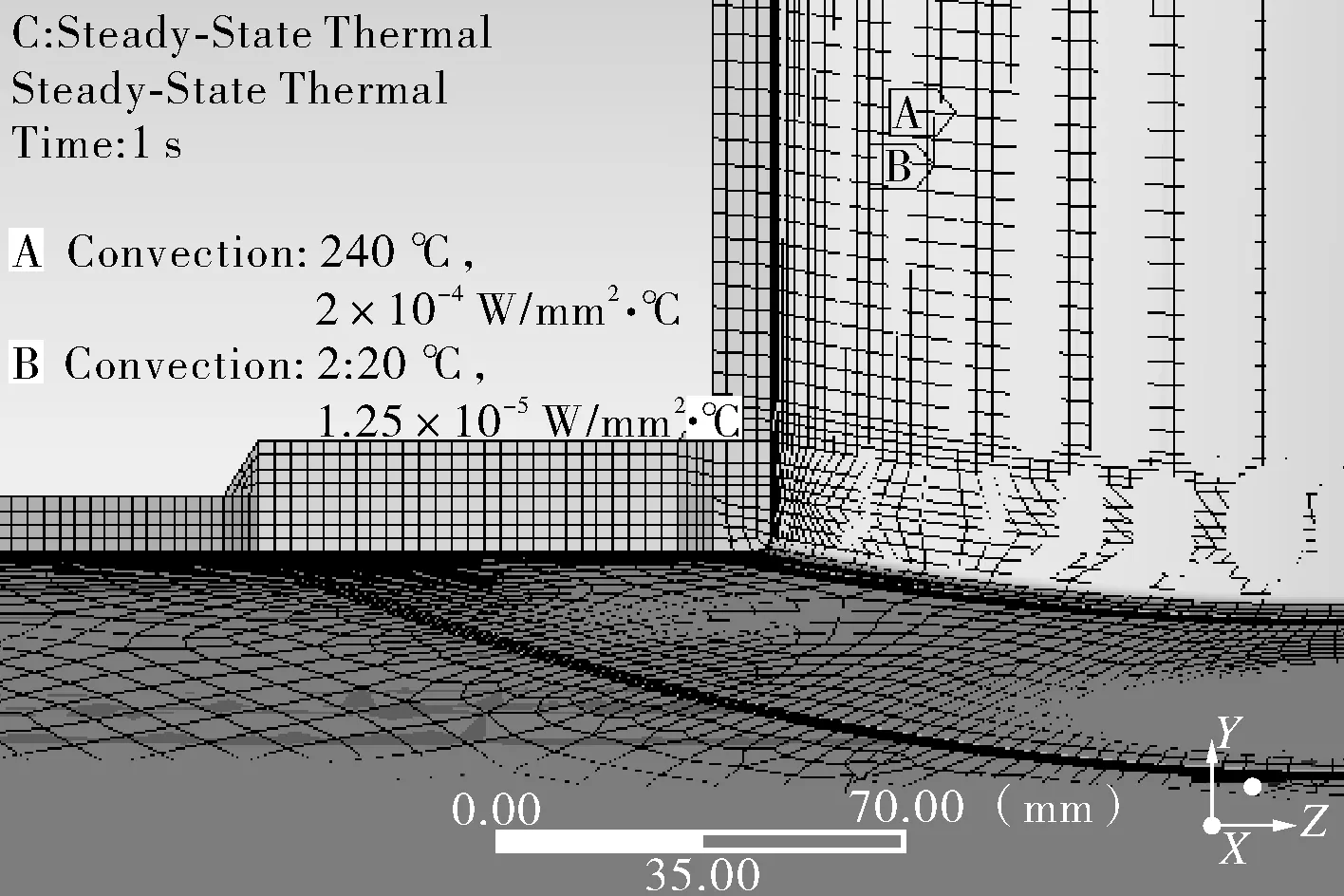
利用有限元法考虑热对流和热传导作用下温差作用的影响：壳体内表面设置介质温度(40～240 ℃)和不同温度下的对流传热系数；壳体和补强圈的材料特性中分别定义不同温度的导热系数和线膨胀系数；补强圈和壳体外表面设置温度为常温20 ℃，对流传热系数为12.5 W/(m2·℃)；补强圈与壳体间隙处设置摩擦接触以传递热和力载荷。图5示出补强圈与壳体之间内压为定值时，接触位置和接触压力随温差的变化趋势。

由图5(a)～(e)分析可知，在内压和温度场耦合作用下，接触位置和接触压力亦最先出现在横向截面区域内外焊缝中间位置处，接触压力随内部设置温度的增加而逐渐增大，在温度达到180 ℃时，接触压力显著增加，接触区域面积则呈现出先减小、后增大的趋势。

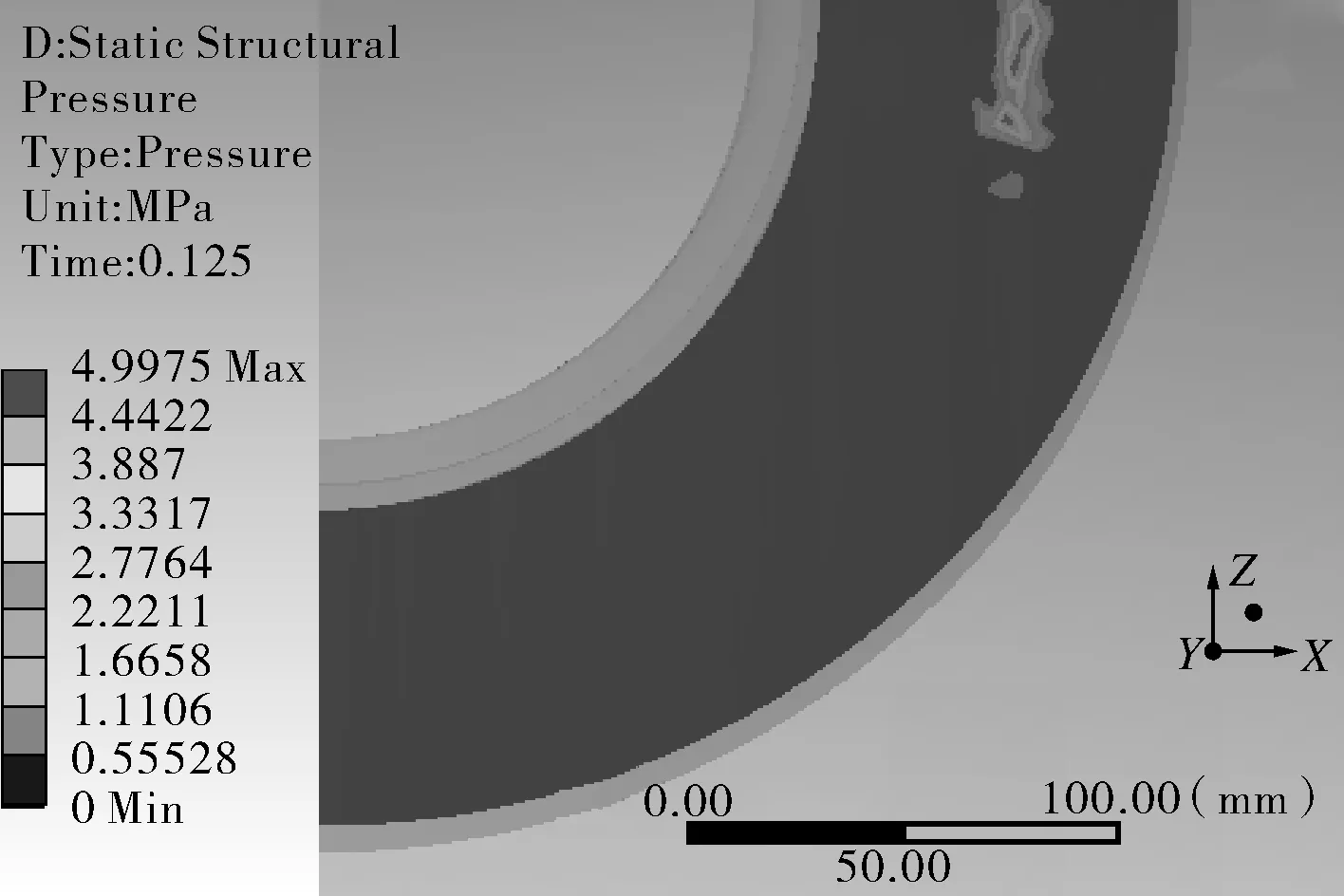
(a)p=4 MPa,T=40 ℃

(b)p=4 MPa,T=80 ℃

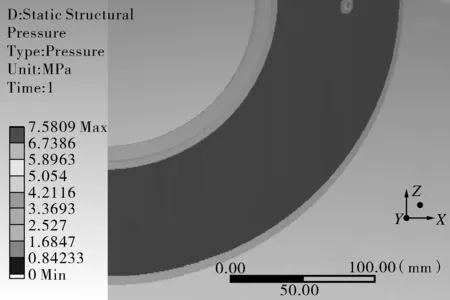
(c)p=4 MPa,T=120 ℃

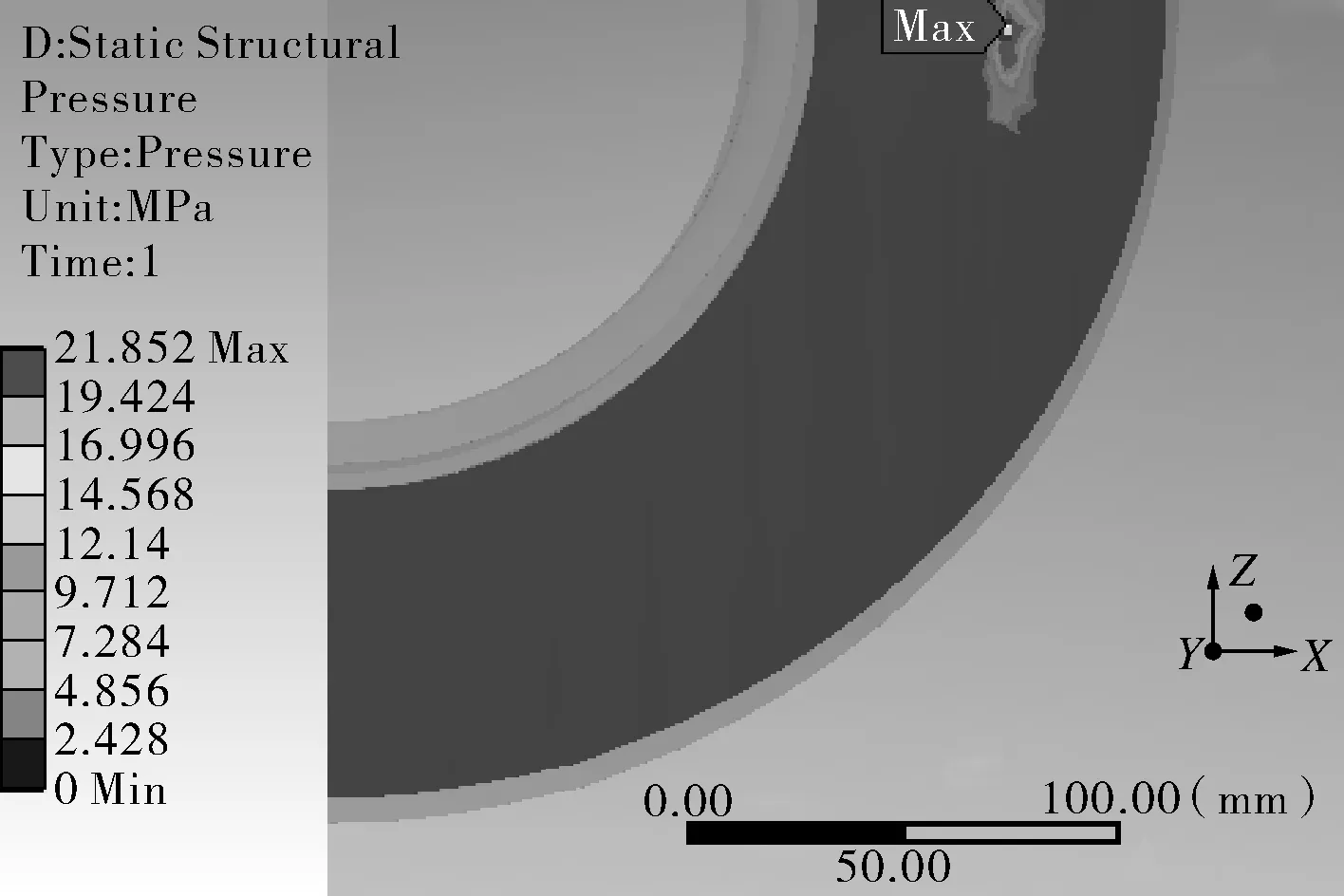
(d)p=4 MPa，T=180 ℃

(e)p=4 MPa，T=240 ℃

(f)温度场分布图

(g)壳体温度分布云图(T=240 ℃)

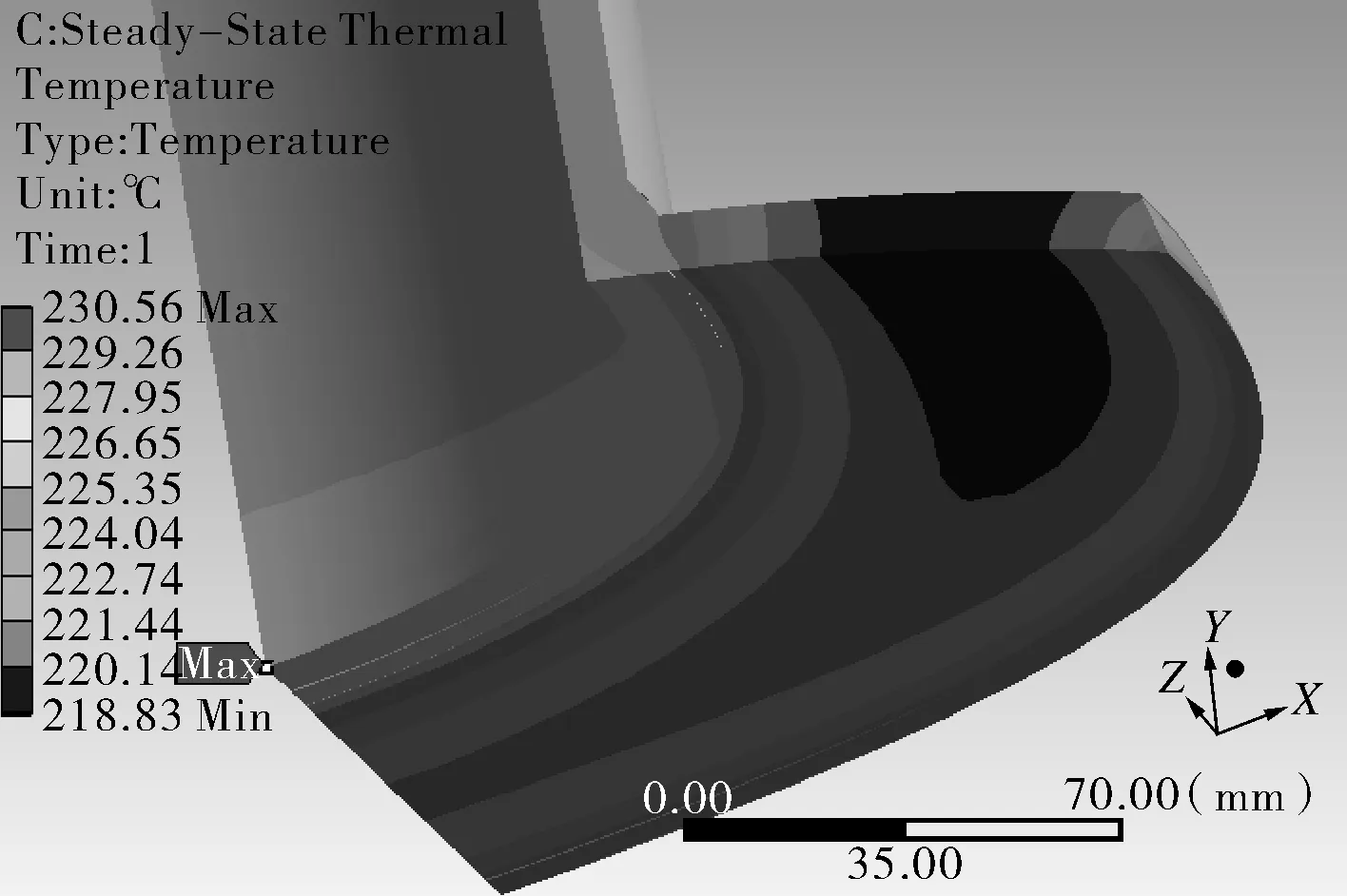
(h)补强圈温度分布云图(T=240 ℃)

图5 补强圈与壳体之间接触位置和接触压力随温差的变化趋势

由图5(f)～(h)可以看出，在横向截面区域，壳体外壁与补强圈内壁之间温差最大，壳体与补强圈的相对变形最大，故最先开始与补强圈接触产生接触压力，随着温差增大，接触压力则越大，接触位置面积先减小后增大的趋势可能是由于在不同温差下、不同位置处变形不同所致。

3.2 补强圈与壳体、接管组合结构应力分析

温差的存在一方面会在总体结构不连续区域产生较大的二次弯曲应力；另一方面则会在局部结构不连续区域产生较大的峰值应力，会对整个结构的总应力分布产生较大的影响。图6示出补强圈与壳体、接管组合结构应力分布趋势。

(a)p=4 MPa,T=40,80 ℃

(b)p=4 MPa,T=120，180，240 ℃

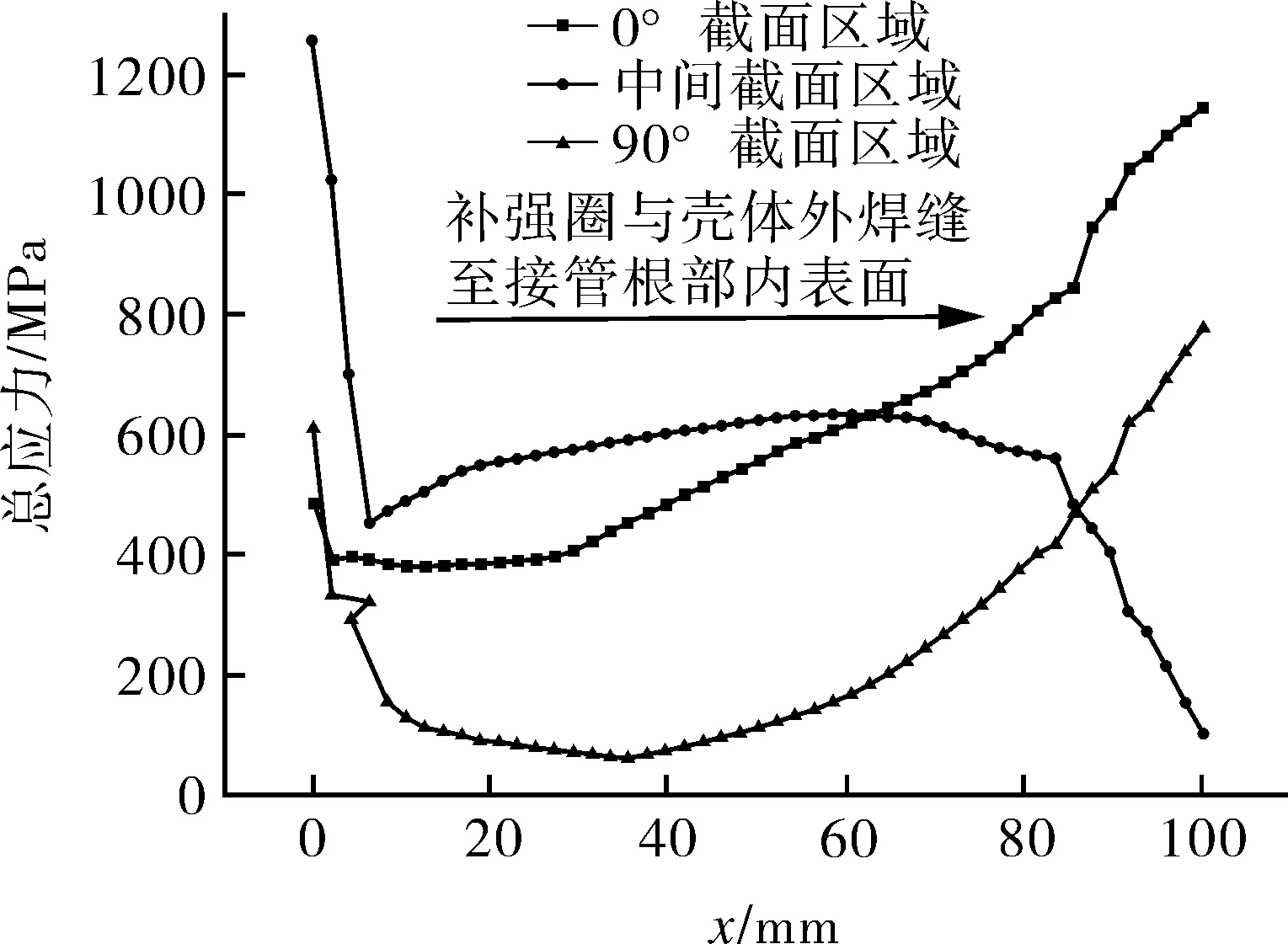
(c)3个区域外焊缝至接管根部内表面各类应力变化曲线

由图6(a)，(b)可以看出，内部设置温度T=40，80 ℃时，最大总应力与内压单独作用时一致，均出现在纵向截面区域(90°)的接管根部内表面位置，说明此时温差较小，对总应力的影响不大，内压对应力分布仍起决定性作用；而在T=120，180，240 ℃导致温差较大时，外焊缝位置的总应力从横向截面(0°)至纵向截面区域(90°)呈先增大、后减小的趋势，在焊缝位置中间段达到最大值，接管根部内表面的总应力则相反，呈现出先减小、后增大的趋势，最大值则由90°截面区域变化至0°截面区域，与内压单独作用下的总应力分布趋势相比已发生了根本性变化。由图6(c)各类应力曲线分析认为：内压与温度场耦合作用下，除位移变形位置发生变化外，温差产生的二次弯曲应力已大于接触压力的影响且起主导作用，同时又附加产生了极大的峰值应力。焊缝位置中间段，一方面由于总体结构不连续产生较大的二次弯曲应力；另一方面由于局部结构不连续产生很大的峰值应力，造成此处总应力值达到最大。在接管根部内表面，其应力组成成分有内压产生的一次应力及同样由温差产生的二次弯曲应力及峰值应力，但在0°截面区域温差产生的二次弯曲应力则远远大于90°截面区域，因而使得0°截面区域总应力值达到最大。综上所述，温差的存在会对补强圈与壳体之间接触特性以及总应力分布趋势产生一定的影响，且温差越大，影响越显著。

4 初始间隙对补强圈接触特性和应力分布的影响

本节初步探讨和对比分析无初始间隙模型和有初始间隙模型的接触特性及其对总应力分布的影响[13](见图7)。

由图7(a),(b)可以看出，在无初始间隙时(Δ=0 mm)，即使在很小的内压作用下，补强圈与壳体之间也会产生一定的接触压力，且接触位置同样最先出现在横向截面区域；而有初始间隙时(Δ≈0.2 mm)，因缝隙的存在且在壳体变形未达到闭合间隙的程度时，补强圈与壳体之间则不会接触亦不会产生接触压力。

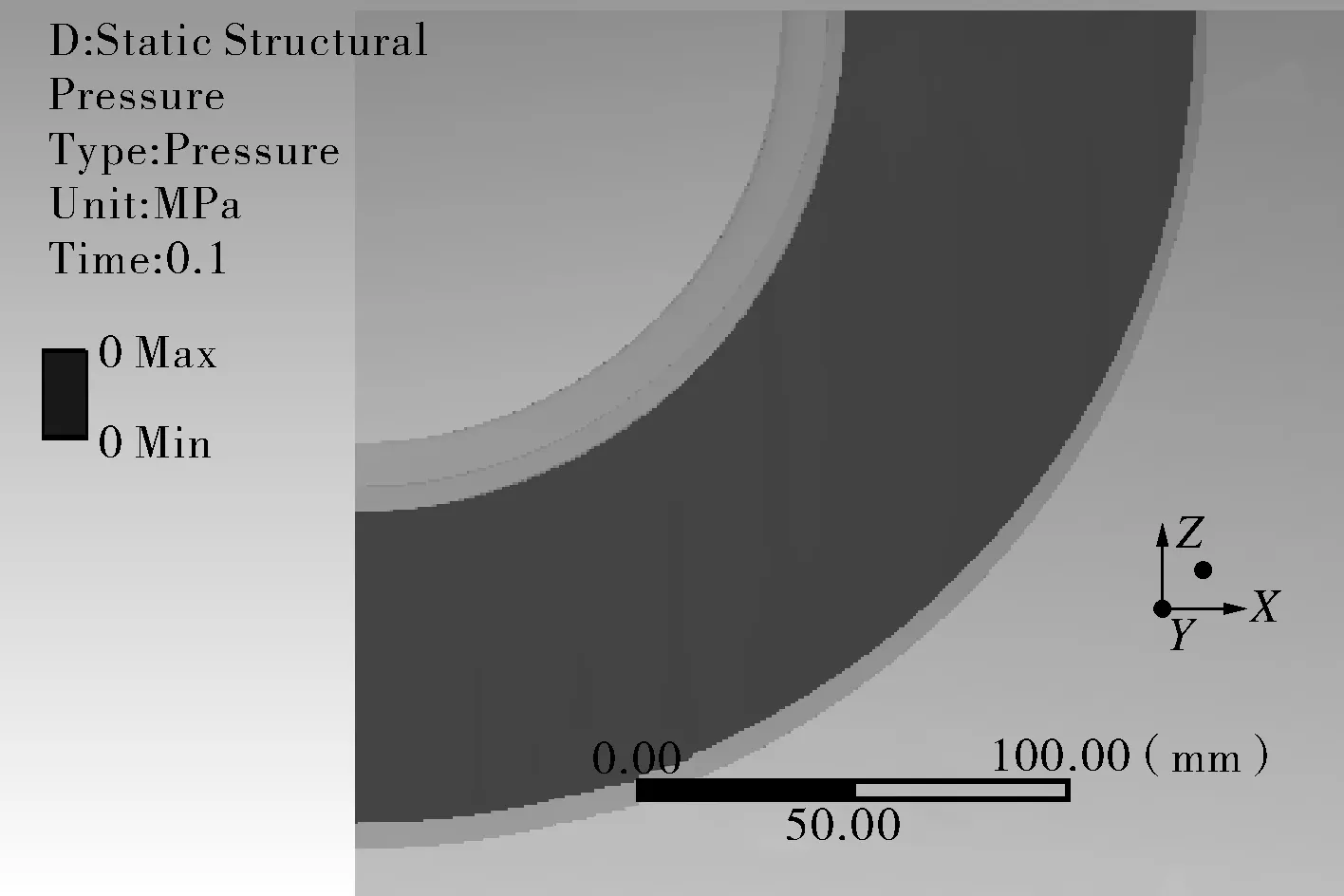
(a)Δ≈0.2 mm，p=2 MPa

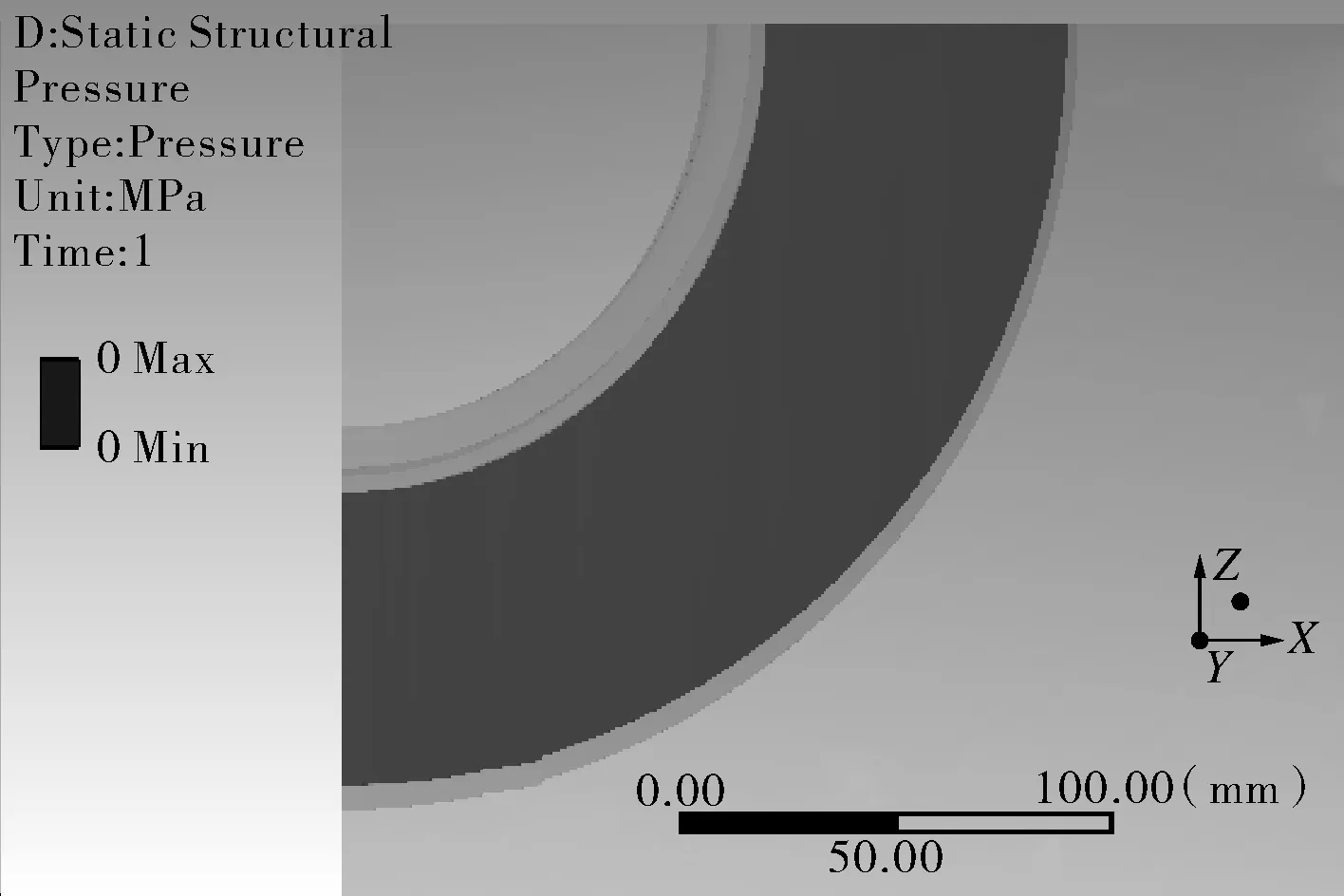
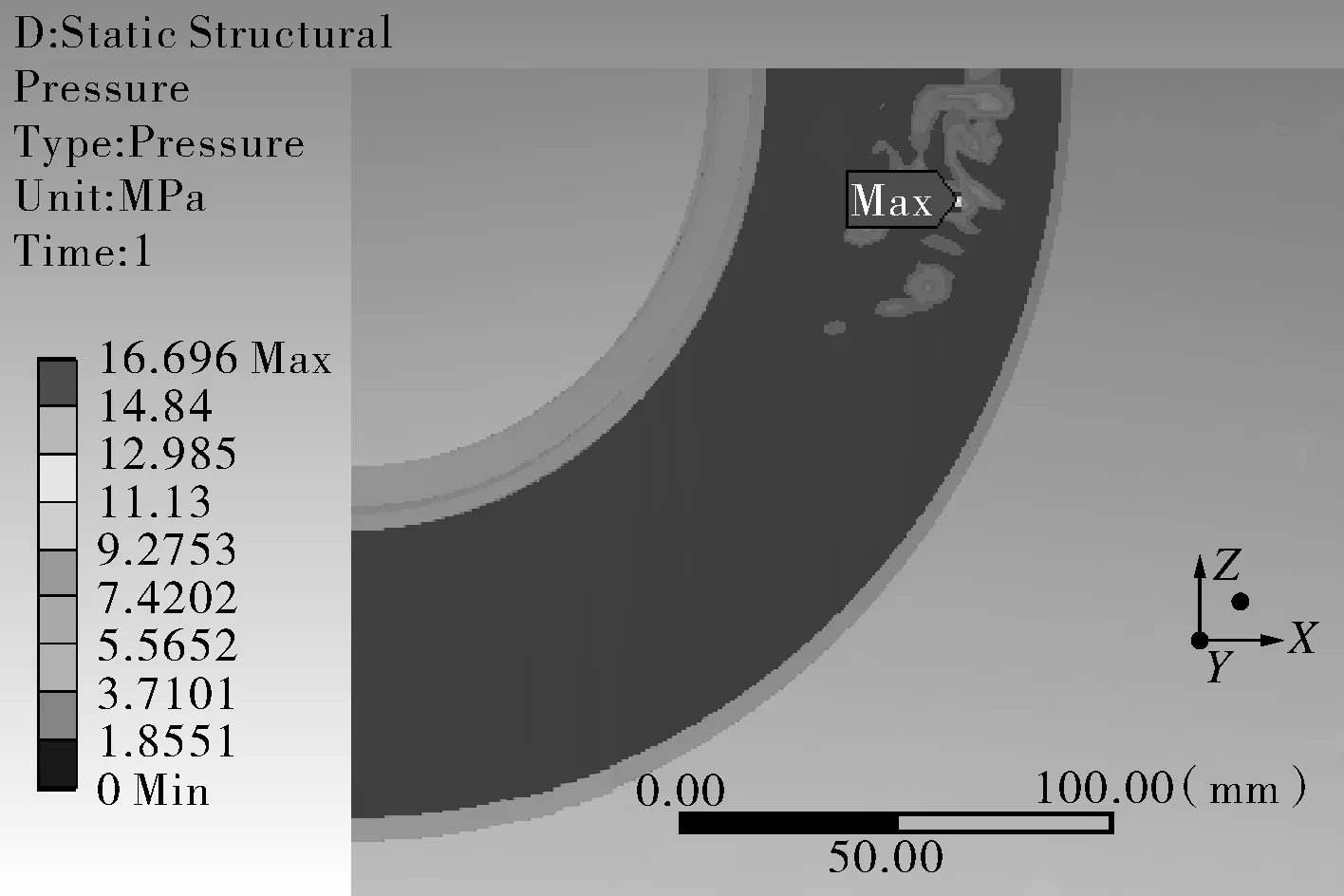
由图7(c),(d)可以看出，在无初始间隙时，温差的存在导致接触压力和接触区域面积的增大；而在有初始间隙时，即使存在一定的温差，只要变形没有闭合间隙，同样不会产生接触压力。另外，可看出，有无初始间隙对结构最大总应力及其分布趋势几乎无影响，在无温度场时，最大总应力出现在接管根部内表面，与间隙无关；在有较大温度场时，最大总应力则出现在补强圈外焊缝中间段，同样与间隙无关，进一步证实了是在温差作用下产生极大的弯曲应力和峰值应力改变了总应力分布趋势。综上所述，可进一步推导出当内压和温差均较大时，接触压力的存在和增大对整个补强结构的总应力分布必然会产生显著影响的结论。

5 结语

本文基于有限元法，以工程中常用的焊接开孔补强圈结构为模型，对该结构在压力和温度场耦合作用下接触特性(接触压力和接触位置)、总应力及各类应力的变化规律进行了分析，以期能够为工程实际提供一定的理论参考和设计依据。

(1)有限元结果分析表明，接触压力是真实存在的，且接触压力的大小对整个结构的总应力分布会产生一定的影响；同时，补强圈与壳体外焊缝位置成为一个局部高应力区域。

(2)内压单独作用下，当补强圈与壳体之间相对变形达到一定值时，两者之间会接触并产生相应的接触压力，且随内压的增大、接触压力逐渐增大；接触位置则最先出现在横向截面区域内外焊缝中间位置处，并逐渐向纵向截面区域过渡，最终使得整个补强圈与壳体接触上，且横向截面区域的接触压力和接触面积始终大于纵向截面区域。

(3)内压单独作用下，最大总应力始终出现在接管根部内表面，且自纵向截面区域至横向截面区域逐渐减小至最小值，而补强圈与壳体外焊缝位置的应力分布趋势则恰恰相反，在横向截面区域应力值为最大。

(4)内压和温度场耦合作用下，接触位置和接触压力亦最先出现在横向截面区域内外焊缝中间位置处，接触压力随内部设置温度的增加而逐渐增大，在温度达到180 ℃时，接触压力显著增加，接触区域面积则呈现出先减小、后增大的趋势。

(5)内压和温度场耦合作用下，内部设置温度较小时，最大总应力与内压单独作用时一致，说明此时温差较小，对总体应力的影响不大；而温度达到一定值使得温差较大时，外焊缝位置的总应力自横向截面至纵向截面区域呈先增大、后减小的趋势，在焊缝位置中间段达到最大值，接管根部内表面的总应力则相反，且最大值已由纵向截面区域变化至横向截面区域，与内压单独作用下的总应力分布趋势相比，已发生了根本性变化。

(6)无初始间隙时，即使在很小的内压作用下，补强圈与壳体之间也会产生一定的接触压力；初始间隙的存在对结构最大总应力和各类应力分布趋势几乎无影响，主要取决于内压和温差的大小，其产生的接触压力对外焊缝位置的各类应力会产生显著的影响。

(7)综合上述分析，不难理解工程规定中对于承受内压较大、或温差较大、或疲劳压力容器不推荐采用补强圈结构的原因[14]：补强圈和壳体外焊缝位置会产生较大的峰值应力和总应力，对应力比较敏感的工况会造成不可预见的破坏性。