基于优化小波阈值的碳氧比能谱处理方法

杨国锋,戴家才,刘向君,2,陈猛,秦昊

(1.西南石油大学地球科学与技术学院, 四川 成都 610500;2.西南石油大学油藏地质与开发工程重点实验室, 四川 成都 610500)

0 引 言

碳氧比测井仪器利用脉冲中子源发射能量为14 MeV的快中子,快中子与地层中的碳氧等元素原子核发生非弹性散射,利用伽马探测器探测产生的次生伽马射线,并记录响应能谱,根据测量能谱中碳氧元素能窗内的计数率计算碳氧比值,结合相应解释图版实现剩余油饱和度的评价[1-2]。

受放射性统计涨落以及仪器稳定性的影响,仪器所测伽马能谱中会存在噪音,影响计数率的统计[3],使计算得到的碳氧比值产生较大误差。因此,在计算碳氧比之前需先对谱数据进行滤波处理。

小波阈值算法是由Donoho于1994年提出的滤波算法[4],该算法利用小波变换来反映信号时域与频域的局部特征。相对于常用的傅里叶变换频率滤波方法,小波变换的多分辨率分析功能可以提取不同时间、不同尺度下的信号性质,因此对非平稳信号具有更好的应用效果[5]。对变换后的小波系数采用阈值处理可以有效压制信号中的噪声,提高信噪比[6]。该算法中最关键的问题是选取合适的阈值函数,常用的阈值函数包括软阈值函数与硬阈值函数2种[7],但这2种阈值函数均会使信号造成不同程度的失真。针对传统小波阈值算法的不足,Vargas等[8]提出了一种具有双阈值的阈值函数并对地震信号进行了降噪处理。Zhang等[9]提出了一种满足二阶可导的阈值函数并运用Stein无偏风险估计自适应的确定阈值。关新平等[10]将模糊理论引入到小波阈值算法中,提出了模糊小波阈值算法并用于图像去噪。但是由于伽马能谱中噪声结构复杂,采用单一的阈值函数始终无法得到最佳的降噪效果。

本文提出了一种具有可调参数的改进阈值函数,该函数采用不同的参数值可获得不同的滤波处理效果,采用遗传算法对函数中的参数进行优选,寻找使滤波效果达到最好的阈值函数参数值。为了使遗传算法在参数优化中有更好的寻优能力,本文引入了反向学习策略对遗传算法进行改进,增强了算法的性能。通过对实测能谱进行处理验证了所提算法的适用性。

1 改进小波阈值函数

对信号采用离散小波变换(DWT)可以将信号分解为不同尺度不同时间上的小波函数的线性组合。在整个小波变换过程中存在2个重要的函数:母小波函数ψ(t)与父小波函数φ(t),两者均满足可积条件。利用父小波函数与母小波函数构成的正交基可以构建小波函数序列,将信号表示为式(1),实现信号的多分辨率分析

(1)

式中,第1项反映了信号的逼近信息,第2项反映了信号的细节信息。由于在小波域内,信号的能量主要集中于绝对值较大的小波系数中,而信号中的噪音由于能量较弱且具有较强的随机性,主要集中于绝对值较小的小波系数中。因此,通过设置适当的阈值将绝对值小于阈值的小波系数置零,再将处理后的系数进行重构就可实现信号的去噪。

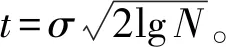
(2)

(3)

硬阈值函数未对大于阈值的小波系数进行处理,和软阈值相比具有更小的均方根误差,即处理后信号和原始信号相比失真较小。但由于硬阈值函数本身存在间断点,滤波后信号会出现附加震荡,出现伪吉布斯效应,影响最终的滤波效果。软阈值函数在整个区间内具有完整的连续性,重构后的信号不会产生附加震荡,但由于对大于阈值的小波系数进行了处理,因此,重构信号和原始信号相比会产生一定的偏差,影响到重构信号和实际信号之间的逼近程度。

本文根据软硬阈值函数的不足与优势,构建了一种新的阈值函数

λt=

(4)

式中,引入了调节参数k,利用参数k可以实现软阈值函数与硬阈值函数之间的过渡。当k趋于0时,改进阈值函数无限逼近硬阈值函数;当k趋于正无穷时改进阈值函数无限逼近软阈值函数。因此,可以通过选择合适的调节参数使滤波效果达到最佳。改进的阈值函数在整个区间上保持了完整的连续性,从而消除了伪吉布斯效应。改进阈值函数与软硬阈值函数的图像(见图1),图1中改进阈值函数的调节参数k取值为0.1。

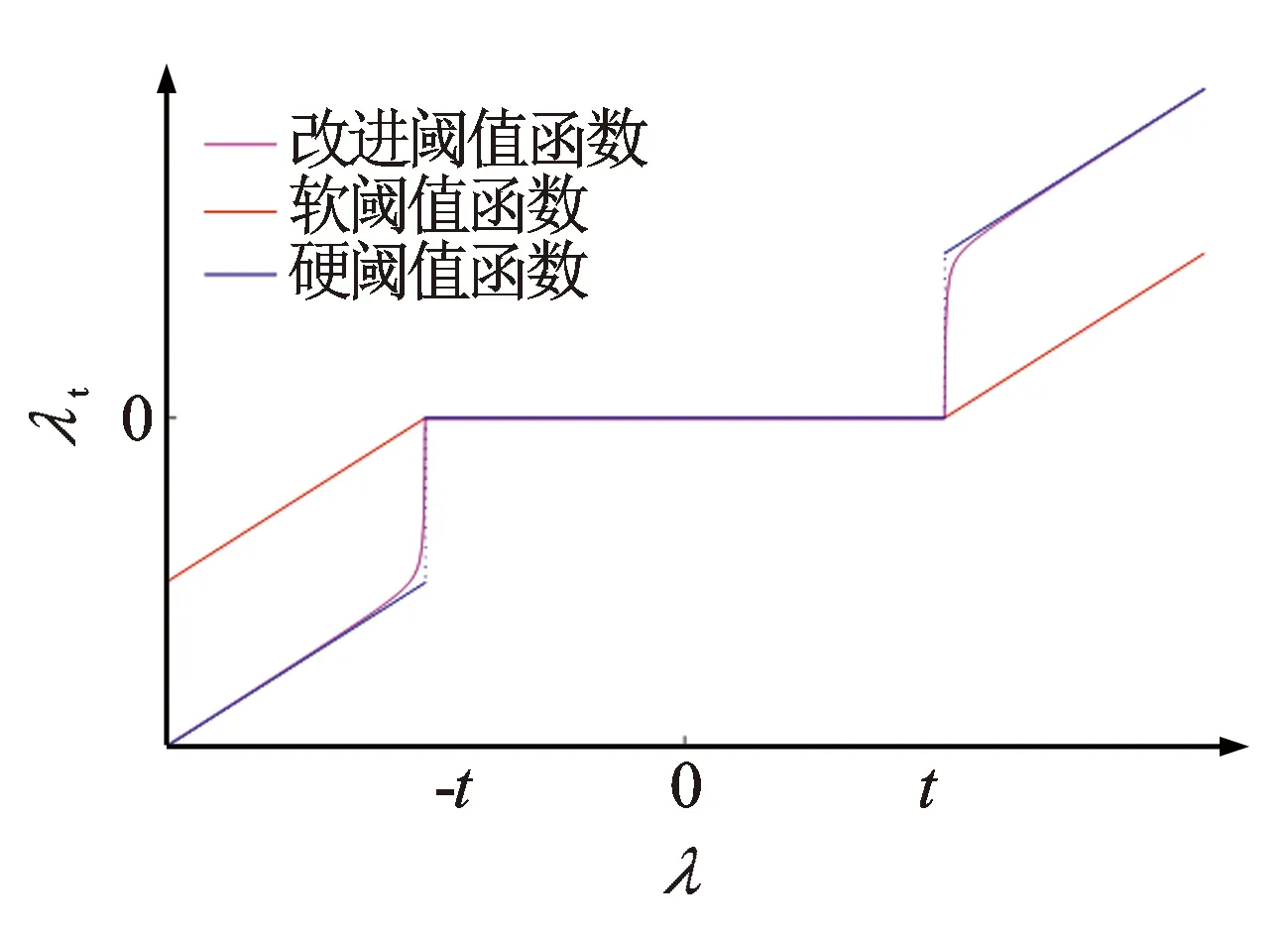
图1 阈值函数对比图像

2 基于反向学习策略的遗传算法

2.1 反向学习策略

反向学习策略(Opposition-based Learning,OBL)是由Tizhoosh于2005年提出的一种智能计算概念[12],前人研究已证实该策略在增强各类优化算法性能上具有良好的应用效果[13-14]。当智能算法评价可行域内个体x的适应性时,同时评价该个体的反向个体可以为优化算法提供更大的搜索范围,此外反向个体往往比当前解更接近最优解,因此,算法的搜索效率也会提升。

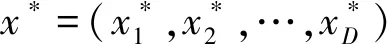
(5)

式中,ai与bi为xi各维下的边界值。但采用式(5)中固定的边界值往往会跳出当前已经收敛的可行域,从而造成已学习信息的丢失,不利于最优解搜索。因此,在反向学习中一般采用动态的边界值[15]

(6)

式中,t表示迭代次数,ai(t)与bi(t)分别为第t次迭代时各维下的边界值

ai(t)=min[xi(t)]bi(t)=max[xi(t)]

(7)

2.2 反向遗传算法

遗传算法是基于自然界遗传机制以及生物进化理论的一种群体智能算法[16]。经典的遗传算法已广泛应用于解决工程中的各类优化问题[17]。但经典遗传算法存在收敛速度慢,易陷入局部最优等局限性。为了增强遗传算法的性能,使其可以更好地实现对小波阈值函数的优化。本文将反向学习策略引入遗传算法中,提出了反向遗传算法(OBLGA),提高了算法适用性。OBLGA的主要操作包括4点。

(1)选择操作。选择操作是根据种群内个体适应性来确定被选择的概率,每个个体被选择的概率与其适应性成正比,采用轮盘赌的方式对个体进行选择,种群中适应性较优的个体有更大的概率被选择进入下一代的迭代

(8)

式中,Pchoose(i)为个体i被选择的概率;fi为个体i的适应性;N为种群中个体数量。

(2)交叉操作。交叉操作从当前代种群中随机选择2个个体,通过交换个体部分染色体片段来产生新的优秀个体。本文设置进行交叉操作的概率为0.4,本文算法中个体采用实数编码的方式[18]

(9)

(3)变异操作。变异操作指从群体中选择一个个体,之后选择该个体染色体中的某一片段重新初始化。通过变异操作可以增加种群的多样性,帮助算法跳出局部最优。经典遗传算法所采用的变异概率为常值,然而固定的变异概率并不适合种群的进化。在迭代初期由于种群多样性较高,此时不应具有较大的变异概率;在迭代后期由于多样性丧失,此时应该赋予种群一个较大的变异概率,来提高种群多样性,帮助算法跳出局部最优。本文构造了如式(10)的变异概率函数,实现了在迭代初期变异概率较小,随着迭代次数的增加变异概率逐渐增大,且变异概率的增长速度逐渐变缓,有利于在后期提高种群的稳定性

(10)

式中,t表示当前迭代次数;参数a和b为调节因子,本文取a=2,b=0.05。

动态的变异概率既有利于在初期保证种群的稳定性,防止已学习的信息丢失,又有利于在后期提升种群的多样性,提高搜索能力。

(4)反向学习操作。在经典遗传算法中引入反向学习操作,提高算法探索能力与搜索效率。采用式(6)计算种群的反向个体,并评价反向个体的适应性,如果反向个体的适应性优于原个体则用反向个体替换原个体加入种群进行下次迭代。但考虑到每次迭代均要评价种群个体的反向个体会给算法造成较大的计算开销。本文引入了反向学习概率Popposite,仅当本次迭代产生的随机数小于Popposite时进行反向学习操作,反向学习概率取值为0.5。

3 优化小波阈值算法

为了得到改进阈值函数中参数k的最优值,首先需要确定一个目标函数来衡量滤波后信号的质量,进而可以通过上述改进遗传算法对参数k进行寻优。信号滤波后的效果有平滑度与相似度2个标准[19]。平滑度定义为滤波后数据与滤波前数据逐差的方差值比,其值越小说明滤波后信号越平滑。相似度可通过均方根误差来衡量,其值越小滤波后信号相似度越高。平滑度S与均方根误差RMSE根据式(11)、式(12)计算

(11)

(12)

式中,f(x)为滤波前各采样点数据;f′(x)为滤波后各采样点数据;n为采样点数。

为使滤波效果兼顾平滑性与相似性,采用降噪后的平滑度S与归一化均方根误差R的加权平均值作为OBLGA的目标函数

fitness=λS+(1-λ)R

(13)

式中,λ为目标函数中平滑度的权重值,通过调节权重值可以实现不同的滤波效果。在伽马能谱处理时,滤波效果并非越平滑越好,平滑度过高通常会使谱峰增宽,造成邻峰重叠与弱峰丢失,不利于进一步的能谱处理[20]。因此,能谱在降噪同时要尽可能减少滤波后数据与原始数据之间的误差,保证两者的相似性,减小数据的失真。基于以上考虑本文取平滑度权重值为0.7,相似度权重值为0.3。

OBLGA优化小波阈值算法的步骤:①读入含噪信号f(x),设置OBLGA算法的主要参数包括:种群个数,最大迭代次数,交叉概率,变异因子等;设置小波基函数与分解层数。②对含噪信号f(x)进行离散小波变换,得到小波系数。③根据初始k值采用改进阈值函数对小波系数进行阈值处理。④采用公式(13)评价各参数k的适应性。⑤算法进行选择、交叉、变异操作以及计算个体的反向个体,并评价适应性。循环迭代直至达到算法结束条件。

4 实测能谱处理

为验证优化小波阈值算法的滤波效果,取某井不同深度点的实测谱线进行滤波处理,并将结果与软硬阈值函数的处理结果进行对比,计算得到的平滑度,归一化均方根误差以及目标函数适应性如表1所示。由表1可以看出,优化小波阈值算法的滤波处理结果在所有处理能谱中具有最小的均方根误差。这说明优化小波阈值算法的处理结果与原能谱数据最为接近,信号失真最小。

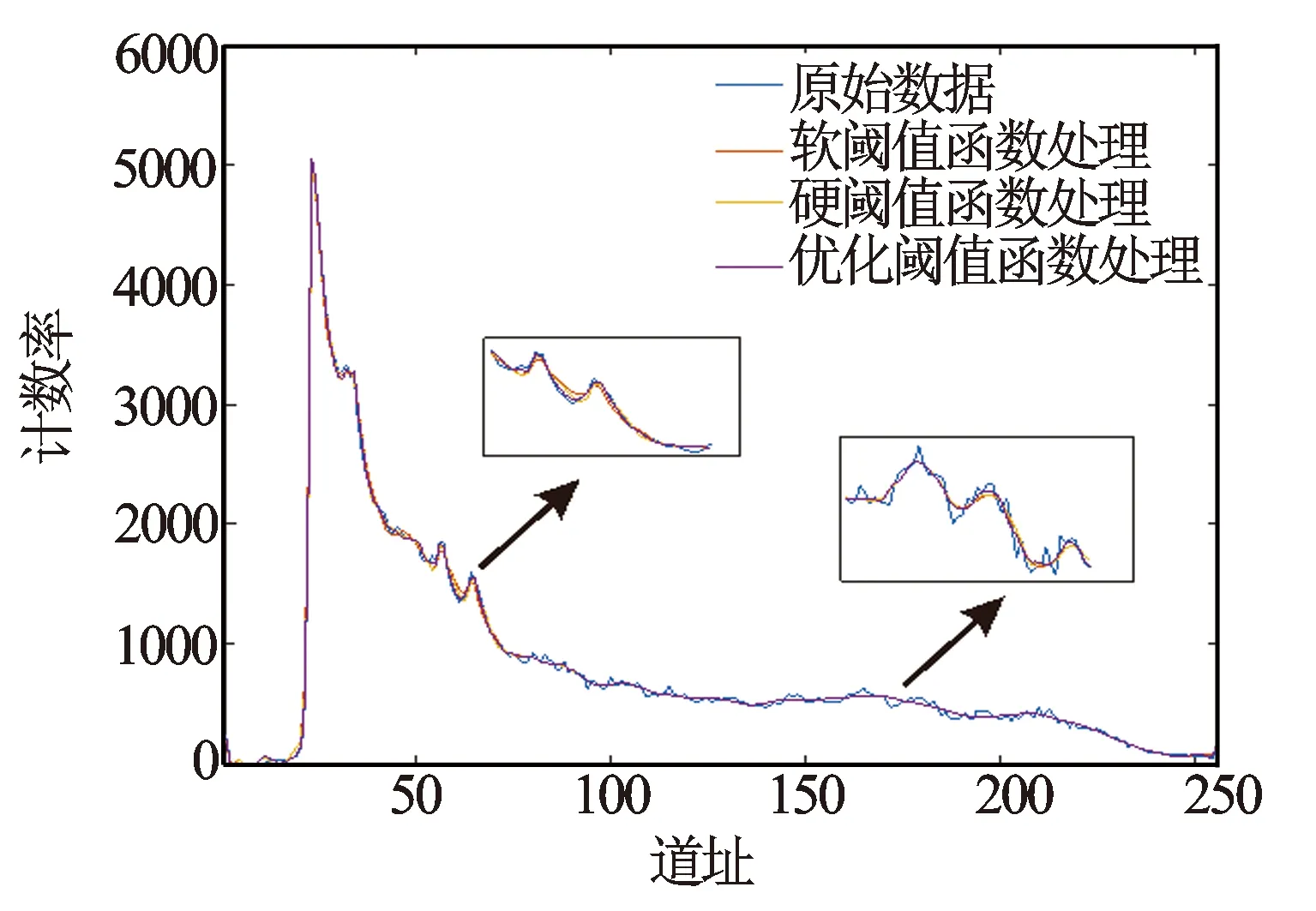
图2 各阈值函数滤波效果对比

软阈值函数处理数据中具有最佳平滑度的谱线占76.92%,说明软阈值函数的处理效果和硬阈值与优化阈值函数相比具有更好的平滑性。但软阈值函数滤波后的能谱数据和硬阈值与优化阈值函数的处理结果相比具有最大的均方根误差,结合图2滤波效果对比图中低能区2个峰的处理效果可以发现,

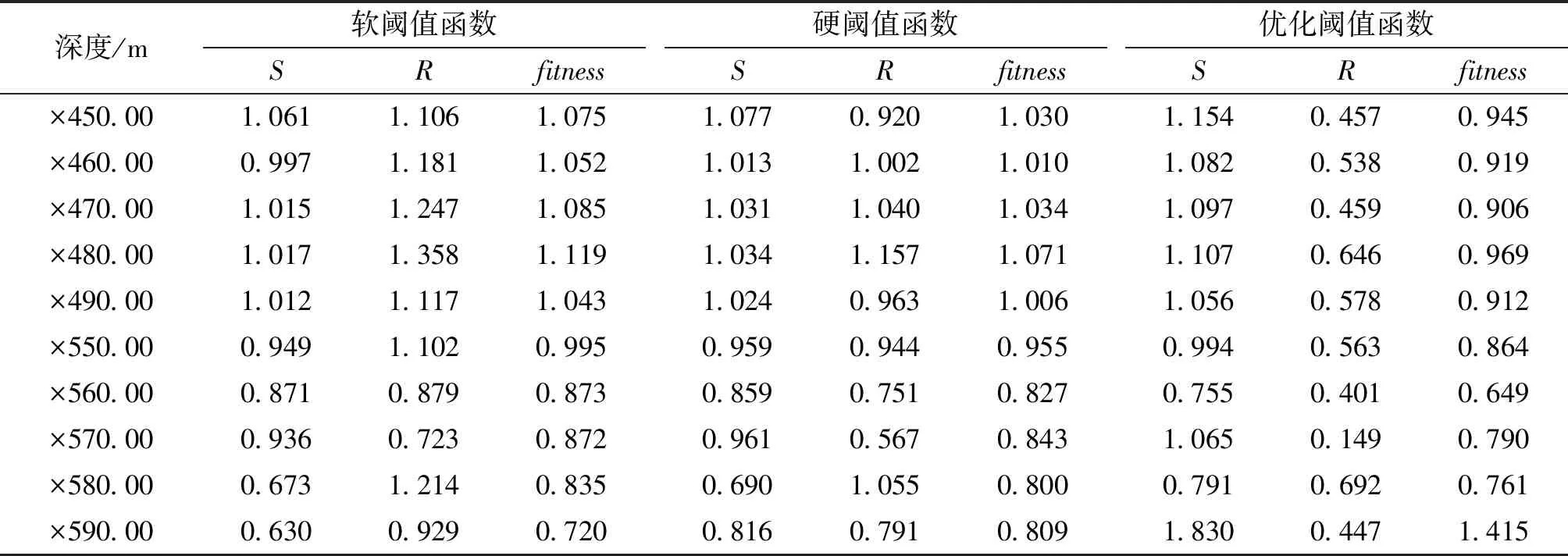
表1 3种阈值函数评价指标对比

软阈值函数处理后的能谱出现峰宽加大,峰高降低的现象,说明谱线出现了过度降噪,这会造成弱峰遗失或邻峰重叠,不利于能谱进一步的处理。而由谱线高能区的滤波图像也可看出采用优化阈值算法处理后的能谱其中的噪声已得到了有效压制。

为考察优化小波阈值算法的实用效果,采用计算滤波处理后的信噪比

(13)

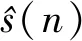
由于不含噪音的纯净能谱数据无法直接获得,因此,采取累加能谱的方式降低统计涨落与噪音影响。选取岩性、物性、含油性变化较小的一小段井段,并将该井段内多张能谱累加并归一化,累加谱和单张能谱相比,噪声占比低很多。本文选取以所选测点为中心的2 m井段内共计20张能谱进行累加并归一化,并将累加后的能谱看作不含噪音的纯净谱,采用式(13)计算信噪比。

将优化小波阈值算法计算的信噪比与硬阈值滤波法,软阈值滤波法,以及传统的滑动平均法与高斯法计算的信噪比进行比较。结果如表2所示。可以看出采用优化小波阈值算法处理的具有最高信噪比的能谱占76.92%。这说明优化小波阈值算法具有更好的实际应用效果。

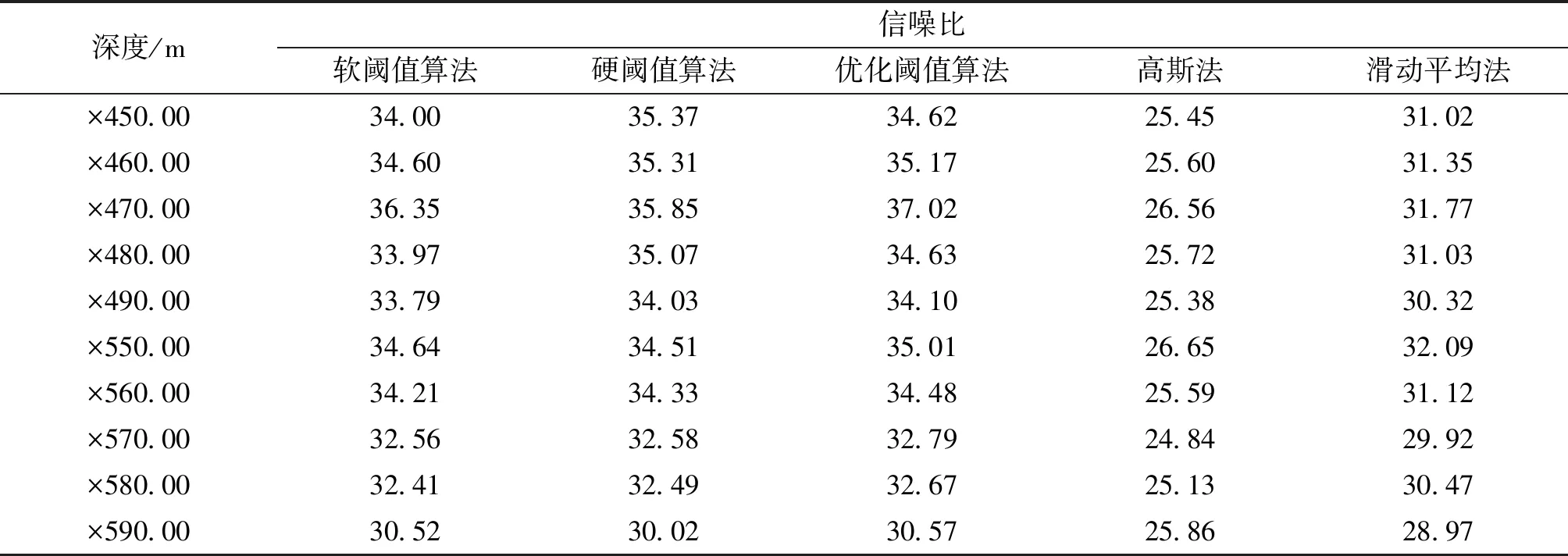
表2 5种滤波算法信噪比对比

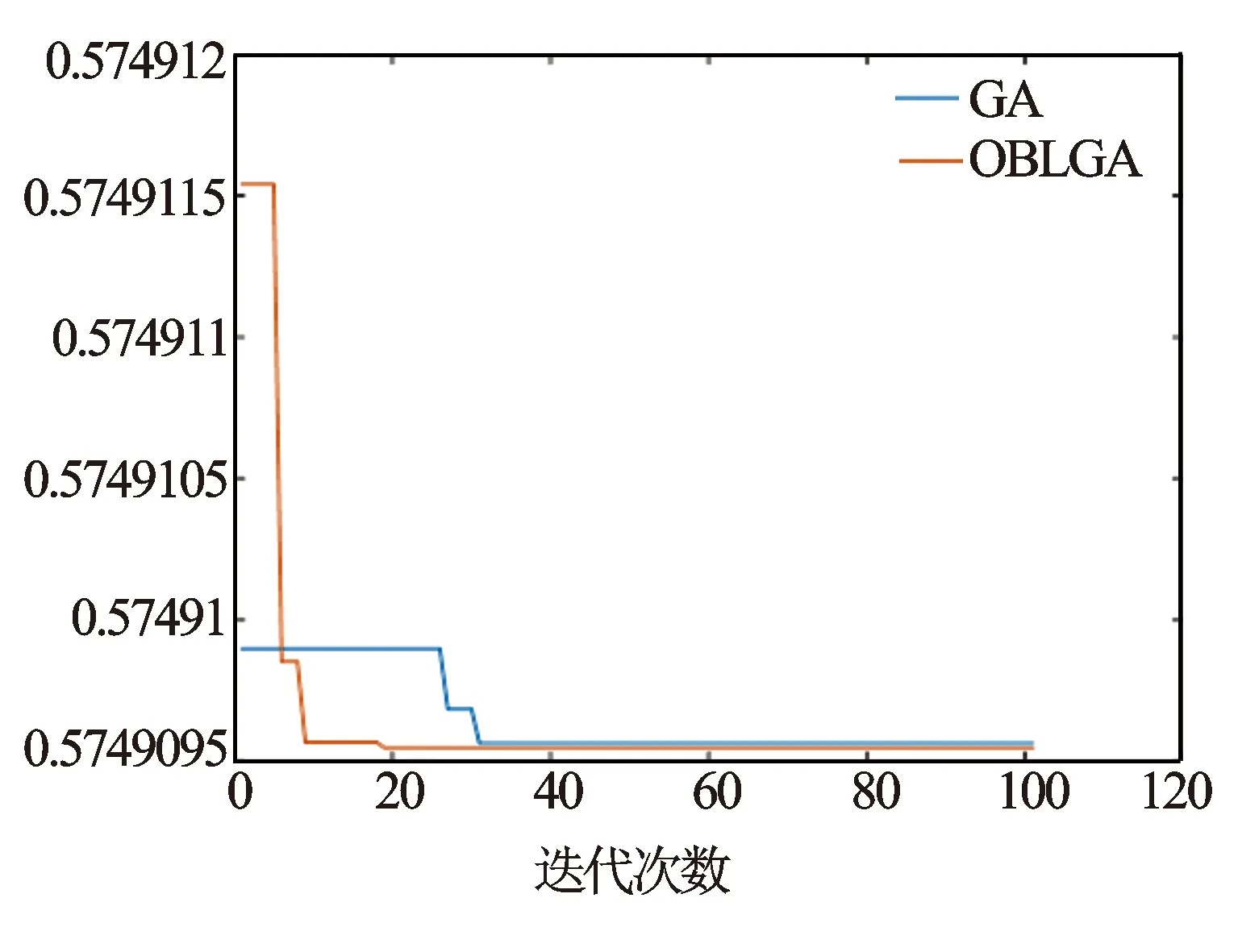
图3 GA与OBLGA迭代曲线

为了说明OBLGA算法在改进阈值函数参数优化中的寻优效果。绘制了GA与OBLGA在参数寻优中的迭代曲线(见图3)。通过曲线对比可以看出OBLGA的收敛速度和GA相比提高了44.4%,并且收敛精度也优于GA。这是由于反向学习策略的引入提高了种群在迭代过程中的搜素范围,使种群个体可以更快地靠近最优解,算法的收敛速度得到了增强。同时动态的变异概率也可帮助算法在迭代后期跳出局部最优解,从而提高了算法的收敛精度。

5 结 论

(1)构建了一种具有调节参数的阈值函数,通过调节阈值函数中的参数可获得不同的滤波效果,并实现了软、硬阈值函数之间的过渡。

(2)为了选取阈值函数的最优参数,提出了反向学习遗传算法(OBLGA),反向学习策略以及动态变异概率的引入使改进算法和经典遗传算法相比收敛性与精度均得到提高。

(3)利用平滑度与归一化均方根误差的加权平均值来衡量滤波效果可防止出现过度降噪,由优化小波阈值算法的处理结果可以看出,优化小波阈值算法处理后的谱线在对噪声有效压制的基础上,和原始数据相比具有更好的相似性,同时和传统方法相比其结果具有更高的信噪比,有利于后期能谱的进一步处理。