吹填淤泥下桶式基础结构土压力及位移分析

曹耀中, 姚文娟,程泽坤

(1.上海大学土木工程系,上海200444;2.中交第三航务工程勘察设计院有限公司,上海200032)

随着我国经济的不断发展,进出口贸易不断增长,使得沿海岸地区的港口工程逐渐向深海地区发展.深海地区多为软土地基,强度差,自然条件也比近海岸区复杂,这对传统水工结构的设计和施工带来一定困难.传统的重力式码头对地基要求高,在软土层较厚的深海地区需要进行大量的地基处理工作,工程投资大,建设周期长,从经济和技术上考虑都不合理.桶式基础驳岸结构是一种新型水工结构,该结构是一种无底的薄壁圆壳结构,具有施工简捷、造价低、耐久性好等特点,能够较好地适应水深、浪大、地基软弱的恶劣环境.目前,国内外学者对桶型基础结构进行了相关的研究[1-5].我国的研究人员依托某港口工程,利用数值模拟与理论计算,对桶式基础结构进行了土压力数值分析、抗倾覆计算、施工及运营期数值模拟等研究[6-8],为大圆筒结构设计及施工提供了理论依据.王元站等[9]采用数值模拟的方法,研究了桶式基础结构上的土压力分布规律,通过与传统土压计算方法的对比分析,提出了更为简洁的土压力计算公式.王广德等[10]利用模型试验,通过数据分析建立了大圆筒结构土压力计算方法.聂琴等[11]对桶式基础结构进行了二维的数值模拟,得到新型结构与土体相互作用的变形规律.蔡正银等[12]、王元站等[13]和文靖斐等[14]通过模型试验或数值模拟,研究分析了桶型结构在波浪荷载下的稳定性.

目前,对于吹填淤泥过程中的桶式基础驳岸结构工作机理的研究较少,其中吹填淤泥过程中的结构土压力及位移变化规律尚未见报道.鉴于此,本工作利用有限元软件ABAQUS分别建立了1.0∼9.0 m厚吹填淤泥和无吹填土的工况,研究桶式基础驳岸结构在不同厚度吹填土工况下的基础筒壁的土压力分布规律,并通过与Rankine主、被动土压力计算结果对比分析,提出土压力的简化计算方法,分析了结构位移变化规律对其稳定性的影响,以期为工程设计和优化提供参考.

1 工程概况

某港区位于我国沿海典型的淤泥质海岸,工程技术问题复杂.由于淤泥质软土地基含水率高、强度差、承载力低等不利因素,传统水工结构需要大量的地基处理工作,经济上不合理,因此工程采用了桶式基础结构的形式.

1.1 桶式结构

桶式基础结构由上下两部分组成:上部是两个空心圆桶相连而成,桶高15.2 m,桶壁厚35.0 cm;下部为带顶板呈类椭圆状的桶体,顶板厚40.0 cm,桶高9.6 m,长轴为30.0 m,短轴为20.0 m.下部桶体内长、短轴方向各有两个隔板,从而将下部桶体分成9个仓体,其中隔板厚度为30.0 cm.桶体基础结构示意图如图1所示.

1.2 水文条件

桶式基础结构位于水深5 m的位置.根据历年的水文资料和水文规范,工程设计水位及对应的波浪要素如表1所示,其中H1%为1%频率的波高.

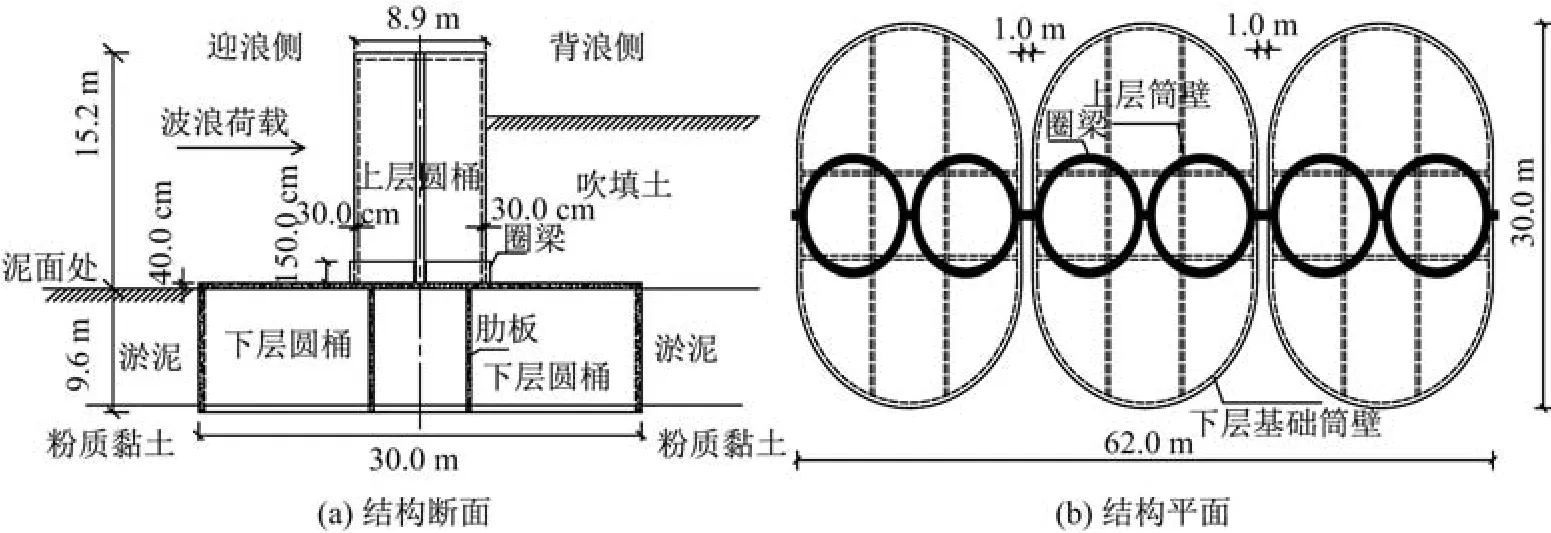
图1 桶式基础结构示意图Fig.1 Diagram of bucket-based structure

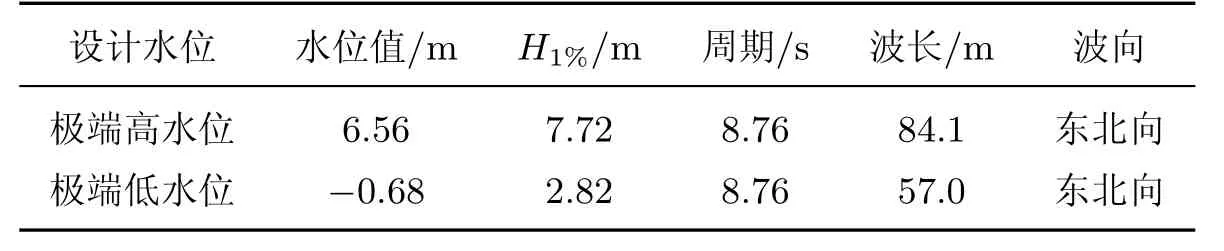
表1 50年一遇设计水位和波浪要素Table 1 Design water level and wave parameters in 50 years

1.3 地质条件

基于实际工程测得结构所处土层的物理力学参数如表2所示.工程所在位置处于计算域范围内地基土为4层:第一层为淤泥质土,第二层为粉质黏土,第三层为粉土和砂土,第四层为粉质黏土.结构右侧吹填淤泥与表2中淤泥质土的力学性能一致.

表2 土层的物理力学参数Table 2 Physical and mechanical parameters of soil layers

2 有限元数值模型

图2所示为吹填淤泥下桶式基础结构的有限元模型.土体的计算域为:宽度为下部桶体短轴的1.2倍,长度为下部桶体长轴的6倍,深度为下部桶体高度的5倍.计算模型边界条件为:计算域土体的端底部设置x,y,z 3个方向的固定约束;地基表面为排水的边界,孔压为0.

在结构-软土地基相互作用系统三维弹塑性模型中,正确模拟软土地基的性质是关键.本工作中土体本构模型采用非线性弹塑性的M-C模型和扩展的D-P模型.与M-C模型相比,扩展的D-P模型在计算黏聚力较小的土体时更易于收敛,但缺点是无法计算土体内摩擦角大于22◦的情况.结合两种本构模型的优缺点,本工作将M-C模型作为扩展D-P模型的补充,即对于土体内摩擦角大于22◦的土层采用M-C本构模型.由于桶体结构刚度远远大于土体刚度,在结构与土的相互作用中,桶体结构自身变形远小于土体,因此桶体结构可采用弹性本构模型.

图2 桶式基础结构的有限元模型Fig.2 Finite element model of bucket-based structure

本工作建立了考虑桩土相互作用的三维弹塑性分析模型.土体结构采用六面体单元,类型为C3D8R,即八节点线性六面体单元,非协调模式.这种网格单元类型的优点是,在弯曲问题中通过桶体与土接触面上厚度方向较少的单元也能保证较高的精度,计算速度快,单元扭曲不大,同时克服了剪切自锁问题,求解位移、应力更准确.模型中土体单元数为24 760,节点数为42 942.桶体结构由复杂的曲面和隔墙组成,采用四面体单元C3D4和六面体C3D8R结合的方式划分网格.四面体单元优势是可以较好地划分形状复杂的几何模型,桶体单元数为10 774,节点数为22 560.

在波浪荷载和吹填土的共同作用下,基础桶内、外壁与土体之间的摩阻力,桶底与底部土的接触压力及摩擦力是结构抗倾覆力的主要组成部分.结构与土体的接触行为是一个高度非线性问题,随时间的变化而不断变化,包括分离、黏结接触和滑动接触等状态.本工作中结构-土体接触模型采用库伦线性摩擦模型,刚度大的桶体结构为主接触面,刚度小的土体为从接触面,法向接触方式为硬接触.当桶式基础结构与土之间分离时,接触压力为0;当桶式基础结构与土互相黏结作用时,接触面处于静止摩擦状态,接触面切向应力为

式中,τc为临界剪切应力,µs为摩擦系数,P为法向接触力.

根据工程实验报告,淤泥层与筒壁之间的摩擦系数为0.04,粉质黏土层与筒壁之间的摩擦系数为0.2.美国石油学会[15]提出:软黏土与桶壁之间的切向摩阻力要小于黏土不排水剪切强度,因此可在接触面属性中增加一个切向应力值,以免出现不符合实际的切向应力.

3 结果分析

3.1 外桶壁竖向方向土压力

通过分析吹填淤泥厚度为3,6,9 m和无吹填工况下的基础桶壁外侧土压力的分布情况,研究吹填淤泥下土压力的分布规律.在吹填淤泥过程中,结构两侧的土压力发育不同.本工作选取下部椭圆桶体迎浪侧中心点处和背浪侧中心点处的土压力为研究对象,土压力分析示意图如图3所示.

图4为不同吹填淤泥工况下土压力沿基础桶壁的分布.在无吹填淤泥的工况下,由于存在波浪荷载,可认为结构绕某点发生转动.由图4(a)可以看出:迎浪侧桶壁与土相互作用发育并不完全,迎浪侧中心点处土压力沿桶壁竖向分布类似于抛物线,呈现先增大后减小的趋势;土压力分布接近于Rankine主动土压力.当桶式基础结构背浪侧存在吹填淤泥时,同一深度节点处的土压力随吹填淤泥厚度增大而增加,这是因为淤泥对桶壁侧压力增加,使得迎浪侧桶壁与土相互作用比无吹填淤泥时更充分.6.0 m吹填淤泥和9.0 m吹填淤泥工况下土压力趋近一致,可认为接近主动土压力极值.0∼8.0 m处土压力分布与Rankine主动土压力分布是一致的,但土压力在8.0∼9.6 m的粉质黏土层比理论值大,说明迎浪侧下部桶壁底部与土的相互挤压比无吹填淤泥工况下更充分.

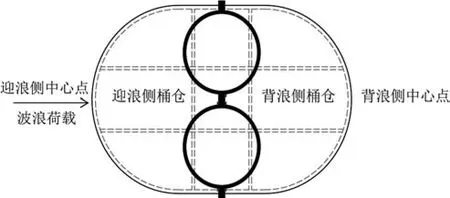
图3 土压力分析示意图Fig.3 Diagram of soil pressure analysis

由图4(b)可以看出,土压力分布趋势靠近被动土压力,但比Rankine被动土压力小.土压力分布的整体变化趋势呈抛物线,底部土压力增大趋势并不明显,说明在吹填淤泥的作用下,3.0 m厚度吹填淤泥(工况1)时不同土层之间的相互影响使得被动土压力发育并不完全,比理论值小,其大小位于主动土压力和静止土压力之间.

由图4(c)可以推断,当吹填淤泥厚度达到6.0 m(工况2)时,由于淤泥对桶型结构的侧向和竖向压力,与波浪荷载相互抵消,桶式基础底部被动土压力发育不充分,土压力在静止土压力与主动土压力之间,整体土压力分布趋势呈抛物线分布.工况2中桶壁底部的土压力变化十分明显,其值在静止土压力和主动土压力之间,说明吹填淤泥厚度越大,其被动区土压力发育越不充分.

由图4(d)可以看出,吹填淤泥厚度为9.0 m(工况3)时土压力分布规律与工况2基本一致,其值接近主动土压力.由于吹填淤泥侧压力和波浪荷载的波压力相互作用,使得工况3的土压力略小于工况2的土压力.另外,工况3下桶壁底部土压力变化十分明显,远小于被动土压力值,说明其桶壁底部与土相互作用并不明显,被动土压力发育不充分.

3.2 土压力简化计算

由上述分析可知,在吹填淤泥荷载作用下,桶式基础驳岸结构竖向土压力分布与无吹填土相比明显不同.当没有吹填淤泥时,由于仅有波浪荷载,桶式基础驳岸结构可认为朝波浪荷载方向发生转动,此时迎浪侧中心点处下部筒壁土压力为主动土压力,背浪侧中心点处为被动土压力.当基础结构进行吹填淤泥时,随着淤泥厚度的不断增加,淤泥土对桶式基础驳岸结构的挤压力也就愈大,直接结果是背浪侧下部桶壁被动土压力相对于Rankine被动土压力要小.

因此,在计算桶式基础驳岸结构抗倾覆、抗滑稳定性计算中,假设桶式基础驳岸结构及其桶内土体运动是基本一致的,可看做是一个整体.本工作中,波浪荷载的波压力要大于吹填淤泥的土压力,桶体结构向背浪侧移动.将桶外软土地基划分成主动土压力区和被动土压力区,波浪侧为主动土压力区,吹填淤泥处为被动土压力区.基础桶体土压力简化计算模型如图5所示.

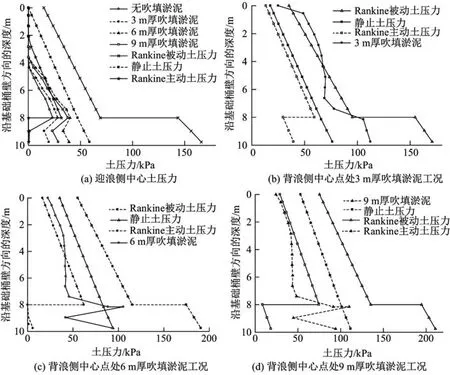
图4 不同吹填淤泥工况下土压力沿基础桶壁的分布Fig.4 Vertical distribution of soil pressure along the wall of bucket-based in different meters thick of silt

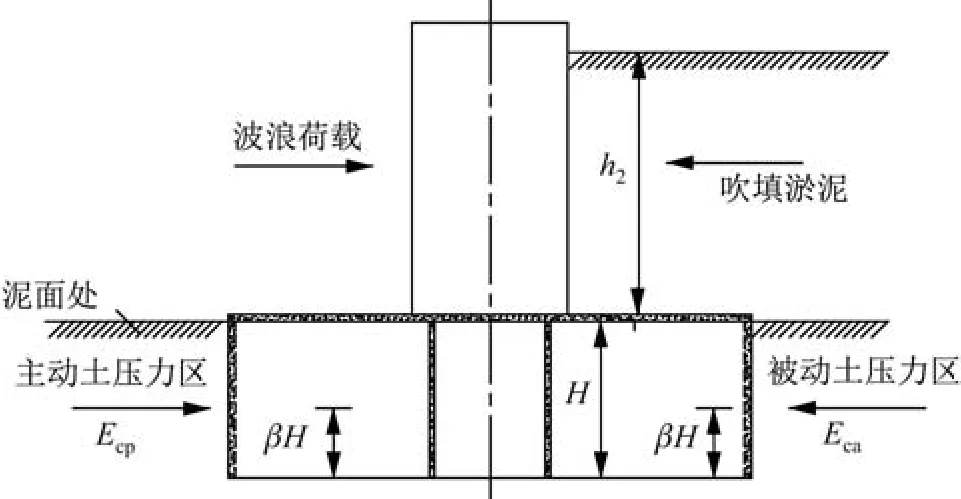
图5 桶式基础结构土压力简化计算模型Fig.5 Simplified computation model of soil pressure for bucket-based structure

为了简化计算,用平直墙面乘以一折减值代替拱形墙面[16],将数值模拟的结果与传统土压力公式的计算结果进行对比,主、被动土压力合力可取传统土压力计算公式的合力乘以一折减值.如果ka为主动土压力修正系数,kp为被动土压力修正系数,则有

式中:Esa,Esp分别为假设平直墙面的主动土压力合力、被动土压力合力;Eca,Ecp分别为Rankine主动土压力合力、Rankine被动土压力合力.合力作用点到基础桶底的高度为

表3是采用不同方法计算的3 m厚吹填淤泥工况下土压力合力及合力作用点位置.根据表3可以看出,简化计算结果和有限元方法计算的结果比较相近,其值均小于Rankine土压力公式得到的结果.这是由于传统的Rankine土压力公式是建立在平直墙面上的挡土墙理论,而桶式基础外壁是连续的光滑曲面,因此土压力分布规律和大小必然存在差异.简化计算方法比有限元方法更加简洁,同时计算结果比传统Rankine土压力理论更精确.根据数值模拟的结果和相应的规范要求,kp取0.6,ka取0.8,β取0.35.

4 位移分析

吹填淤泥下桶式基础驳岸结构的变位分析是稳定性分析的重要内容.本工作中选取迎浪侧中心点处、基础结构中心点和背浪侧中心点处的位移进行分析,变位分析节点如图6所示.

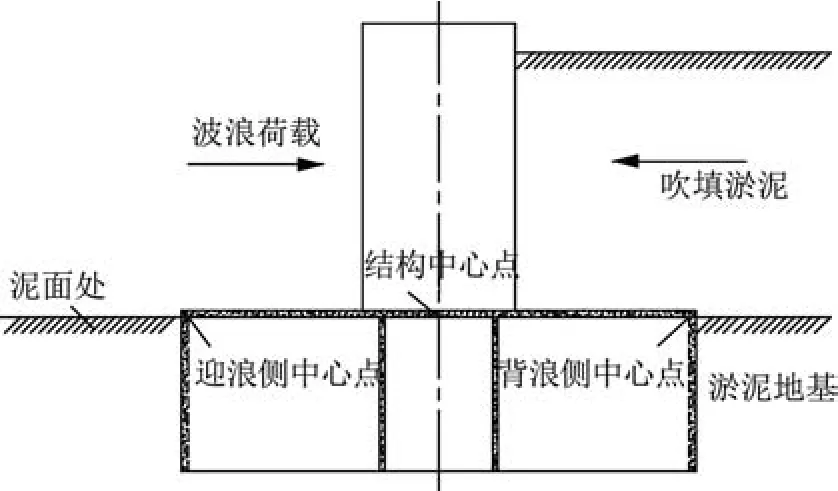
图6桶式基础结构变位分析节点示意图Fig.6 Diagram of displacement analysis for bucket-based structure

图7 为桶式基础结构在吹填淤泥过程中的位移.从图7(a)中可以看出:在吹填淤泥厚度为1.0∼3.0 m时,由于淤泥重力作用在基础桶体背浪侧,使得结构绕某点向海岸侧转动加大,迎浪侧中心点处竖向位移增大;当淤泥厚度持续增加时,竖向位移不断减小.

从图7(b)可以看出,随着吹填淤泥厚度的增加,基础桶体中心点的竖向位移向重力方向不断增大,总体呈线性增加的趋势.背浪侧中心点处的竖向位移向重力方向不断增加,总体呈抛物线趋势(见图7(c)).通过数值模拟可以算出,在1.0∼9.0 m厚吹填淤泥下,桶式基础驳岸结构的转动明显增加,最大转角是无吹填淤泥时的1.24倍,最大沉降则为1.16倍.另外,背浪侧中心点处的沉降率呈单调递减的趋势,没有明显的拐点,说明吹填淤泥过程中桶式基础结构并不会突然失稳破坏,其稳定性在可控范围内.

由图7(d)可以看出,桶式结果中心点处的水平位移为8.0∼9.0 cm,曲线呈先增大后减小的分布规律.桶式基础结构在吹填淤泥作用下整体向海岸侧移动,吹填淤泥厚度为6∼9 m时水平位移回落.

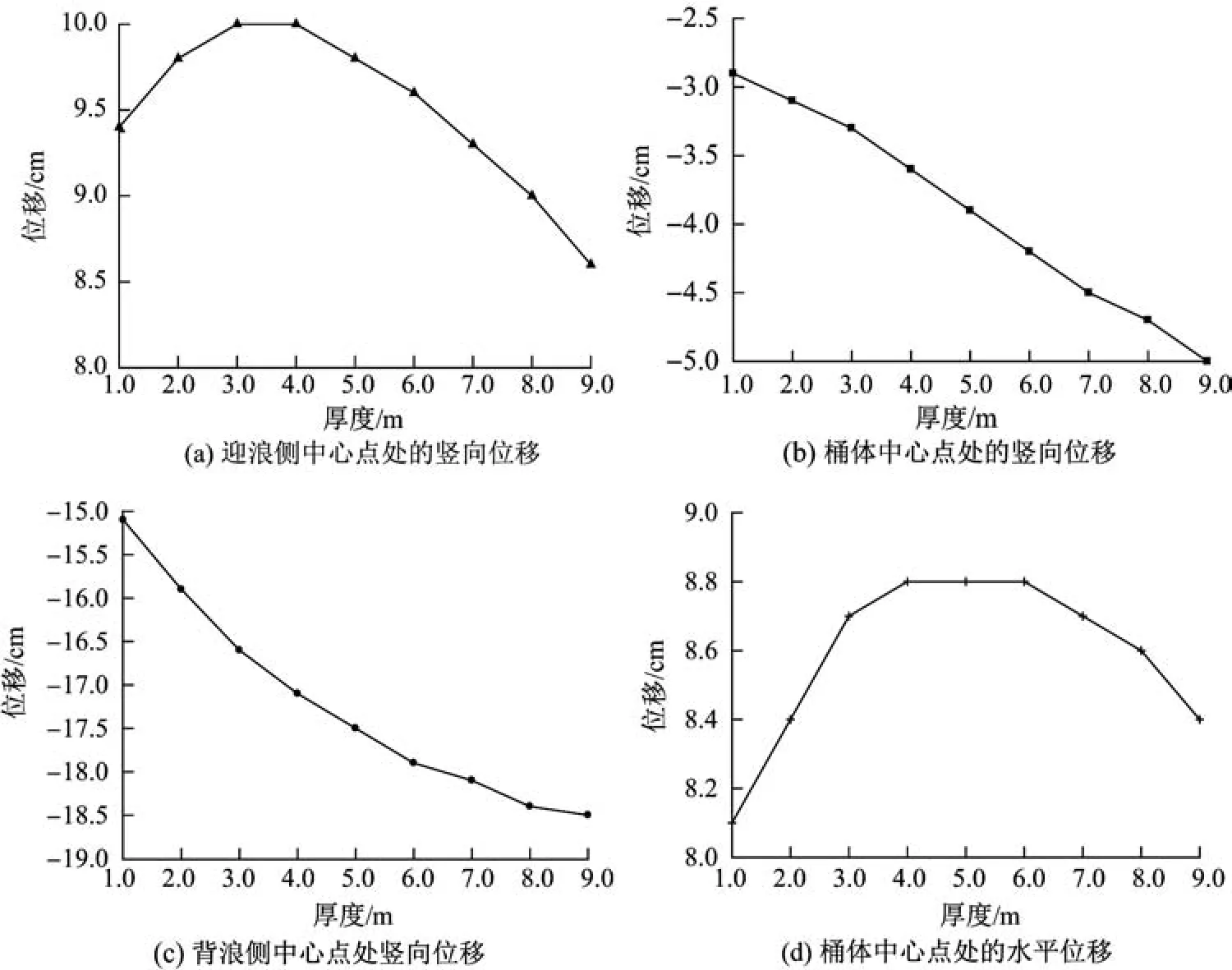
图7 桶式基础结构在吹填淤泥过程中的位移Fig.7 Displacement of the bucket-based structure with different deep thick silt

5结论

(1)通过数值模拟与传统Rankine土压力公式计算对比分析发现,土压力分布趋势与Rankine土压力理论计算结果大致相同.在淤泥层(0∼8.0 m)中,数值模拟的土压力增加速率要大于传统Rankine土压力理论,但是桶体同一深度处土压力数值模拟的结果偏小;在粉质黏土层(8.0∼9.6 m)中,由于桶体底部与土体扰动,使得此处的土压力变化较大,数值模拟的被动土压力要远小于郎肯被动土压力.随填淤泥厚度的增加,基础桶体迎浪侧的主动土压力增大,背浪侧的被动土压力减小.

(2)桶式基础结构与经典挡土墙存在一定差异,其土压力没有相应的计算公式和规范可供参考,简化计算方法和数值模拟方法在结果上比较接近,数值上都小于Rankine土压力理论.相较于有限元方法,简化计算方法速度大为提高,简化计算方法主动土压力与传统Rankine土压力理论值的误差约为25%,被动土压力与传统Rankine土压力理论值误差值约为40%.简化计算方法的精确度要高于Rankine土压力公式,可为工程的设计和施工提供一定的参考依据.

(3)桶体结构在波浪荷载作用下,整体向海岸侧移动,当海岸侧吹填淤泥时,水平位移减小,但是靠海岸侧桶体的沉降随吹填淤泥厚度增加而增大,且沉降速率比水平位移速率变化快.当吹填淤泥的厚度达到工程最大厚度9.0 m时,结构水平位移为8.4 cm,结构最大沉降为18.5 cm,转角为0.42◦.由于这3个值均在规范的允许范围之内,因此结构不会出现失稳破坏.