带有三角函数的二维分数阶离散系统的混沌现象

刘明明, 夏铁成,王金波

(1.上海大学理学院,上海200444;2.中国电子科技集团公司第三十研究所国家保密通讯重点实验室,成都610041)

分数阶微积分作为数学建模的一种可靠工具,在过去几十年中得到了广泛的应用,并取得了丰硕的成果.离散分数阶微积分是分数阶微积分在时间尺度下的理论发展[1-3],被用来描述离散时间的动力学行为,已取得的成果主要有Taylor级数[4]、分数阶差分定义及其性质[5-6]、Laplace变换[7]等.然而,目前对动力学行为方面的研究较少.本工作在一个带有三角函数的二维离散混沌系统的基础上,利用分数阶差分构造了一个新的混沌系统,并刻画了其混沌现象,以更加深入地理解离散动力学行为.

1 带有三角函数的二维离散混沌系统

考虑一个具有如下形式的离散混沌系统[8]:

利用Jacobian矩阵法得到系统(1)的2个均大于0的Lyapunov指数:λ1=1.474 10,λ2=0.820 19.所以,系统(1)的运动是混沌的,而且下面的数值模拟也说明了这一点.

取n=100,图1(a)和(b)为系统(1)在初始值为(0,0)时的解;当初始值的x坐标依步长1.6从−8到8,y坐标依步长0.1从−0.5到0.5时,可得到系统(1)的相位图,如图1(c)所示.

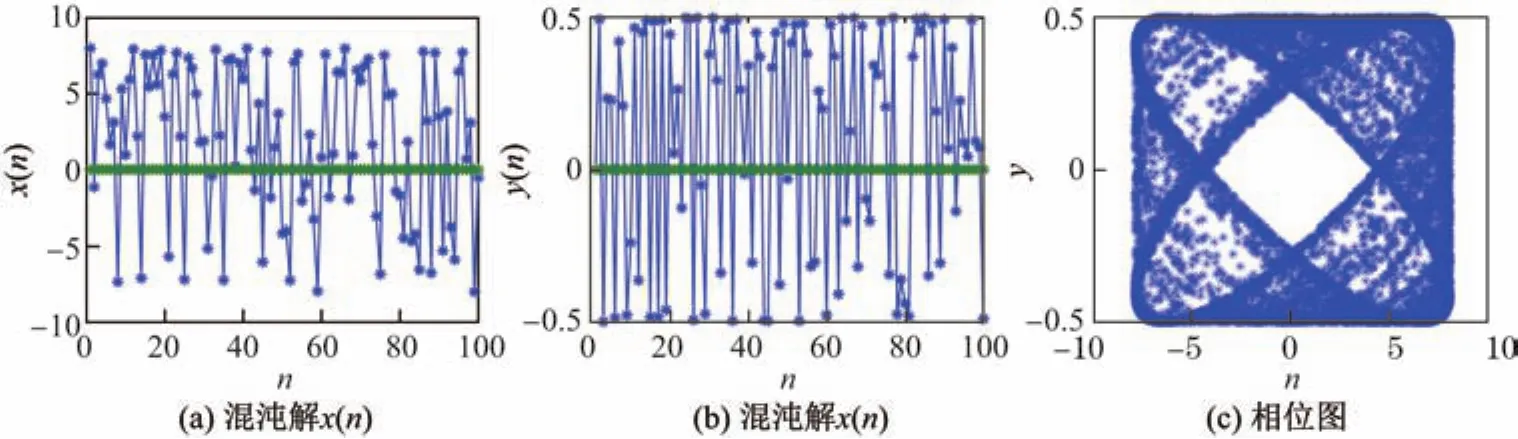
图1 系统(1)中的混沌Fig.1 Chaos in system(1)

2 离散分数阶微积分

在推广之前,首先介绍与离散分数阶微积分相关的概念[1,5,9].

考虑阶乘多项式

这里Γ指Gamma函数,并且如果对于某些j有t+1−j=0,则约定值为零.对n进行扩展,有定义

迭代地定义算子∆j= ∆(∆j−1),这里j是非负整数,∆0表示恒等算子并且∆1f(t)=∆f(t)=f(t+1)−f(t).令Na表示离散的时间尺度,Na={a,a+1,···},其中a∈R固定.考虑具有如下形式的初值问题

这里σ(s)=s+1.注意到,当s=t− (n− 1),···,t−1时,=0,有

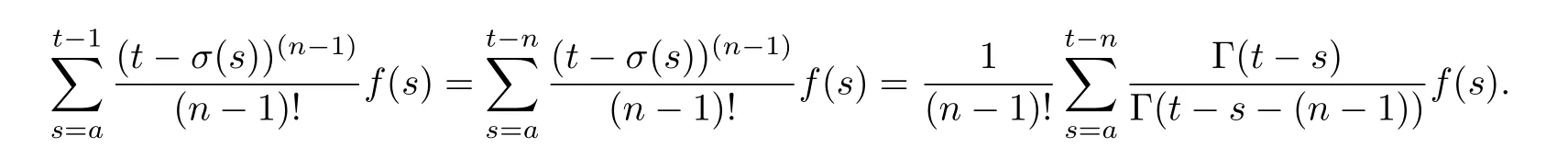
于是,有如下定义.

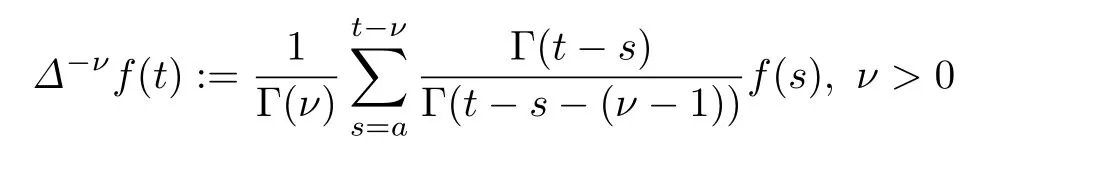
定义1 设ν>0且σ(s)=s+1,那么被称作f的ν阶分数阶和.注意到,∆−ν把定义在Na上的函数映射到了Na+ν上.

利用定义1可以定义函数f的ν阶Caputo分数阶差分如下.

定义2令ν>0,ν/∈N,定义

为函数f的ν阶Caputo分数阶差分,其中n=[ν]+1.

如果ν=n∈N∗,那么

同样地,要注意C把定义在Na上的函数映射到了Na+(n−ν)上.

引理1[10]对于Caputo分数阶差分方程

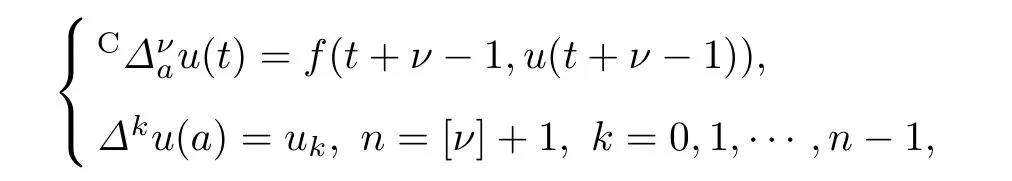
可以获得其等价方程

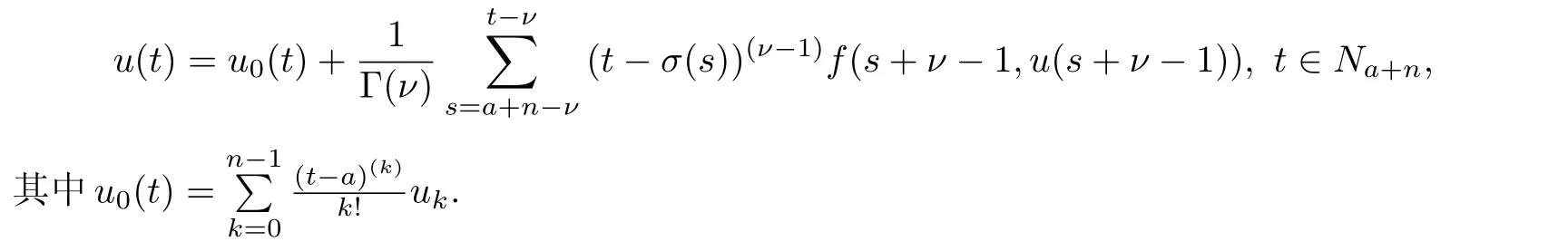
3 分数阶的相应离散混沌系统

对于系统(1),第一个方程可改写为

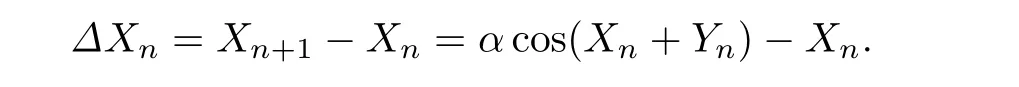
于是,扩展后的ν(0<ν<1)阶Caputo分数阶差分方程可设为

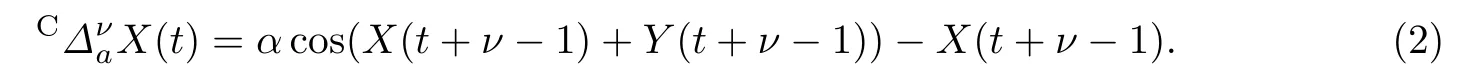
由引理3,可得方程(2)的等价方程

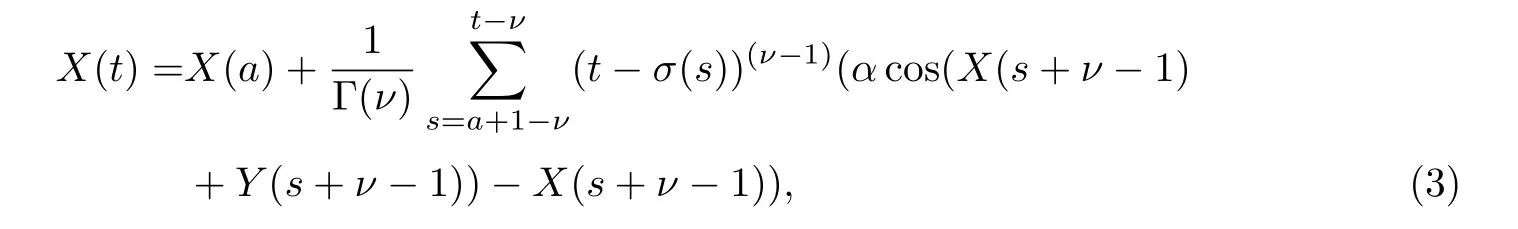
这里t∈ Na+1.记j=s−a+ν,t=n+a,n=1,2,···,另记x(j)=X(a+j),y(j)=Y(a+j),∀j ∈ {0,1,···,n}.则方程(3)可改写成

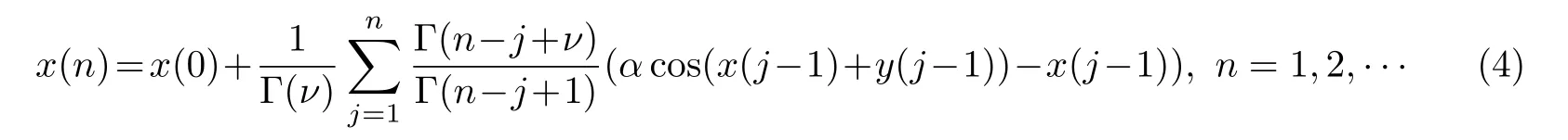
所以,系统(1)扩展后的形式为

4 分数阶离散系统的混沌现象

根据式(4)很容易发现,x(n)依赖其过去的信息x(0),x(1),···,x(n−1),将该现象称为系统的离散记忆效应.当ν=1时,系统(5)正是系统(1).当ν取不同值时,系统(5)对应不同的混沌现象.

首先考虑x关于参数α的分岔现象.取n=100,初始值为(0,0),α依步长0.01从0到1.00,β=0.01固定,则x关于参数α的分岔图如图2所示.

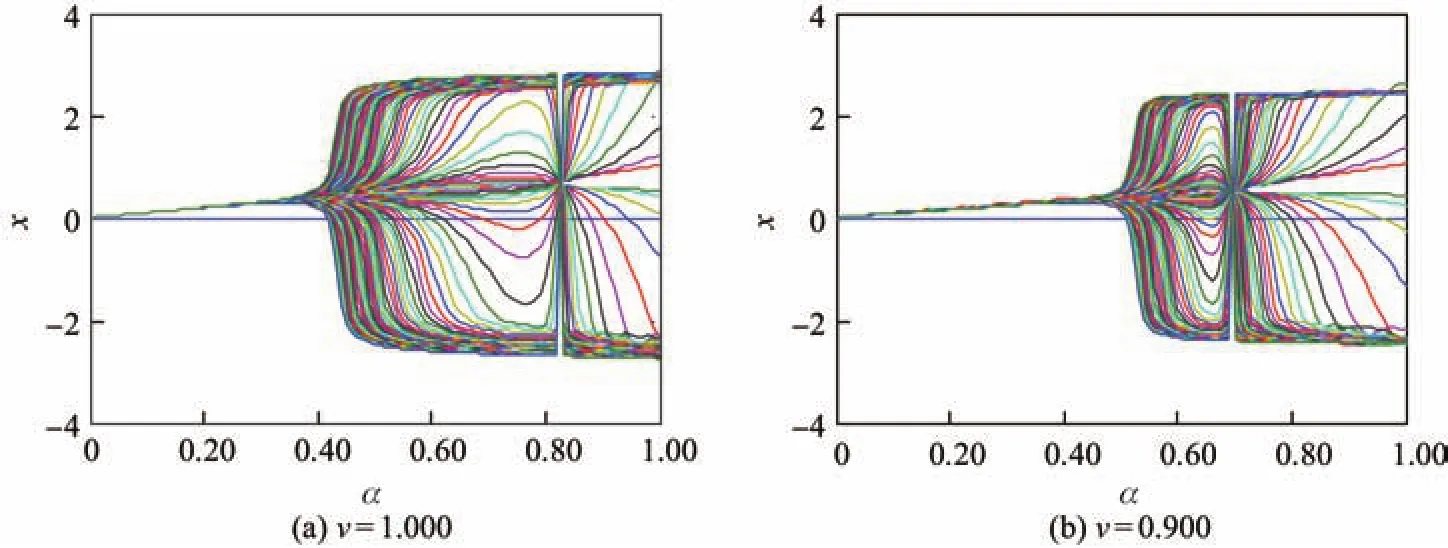
图2 x关于参数α的分岔图Fig.2 Bifurcation diagrams of x concerning α

类似地,仍取n=100,考虑系统(5)在初始值为(0,0)时的解,以及当初始值的x坐标依步长1.6从−8.0到8.0,y坐标依步长0.1从−0.5到0.5时,系统(5)的相位图.图3∼5分别刻画了ν=0.999,0.900以及0.850时系统(5)的混沌现象.

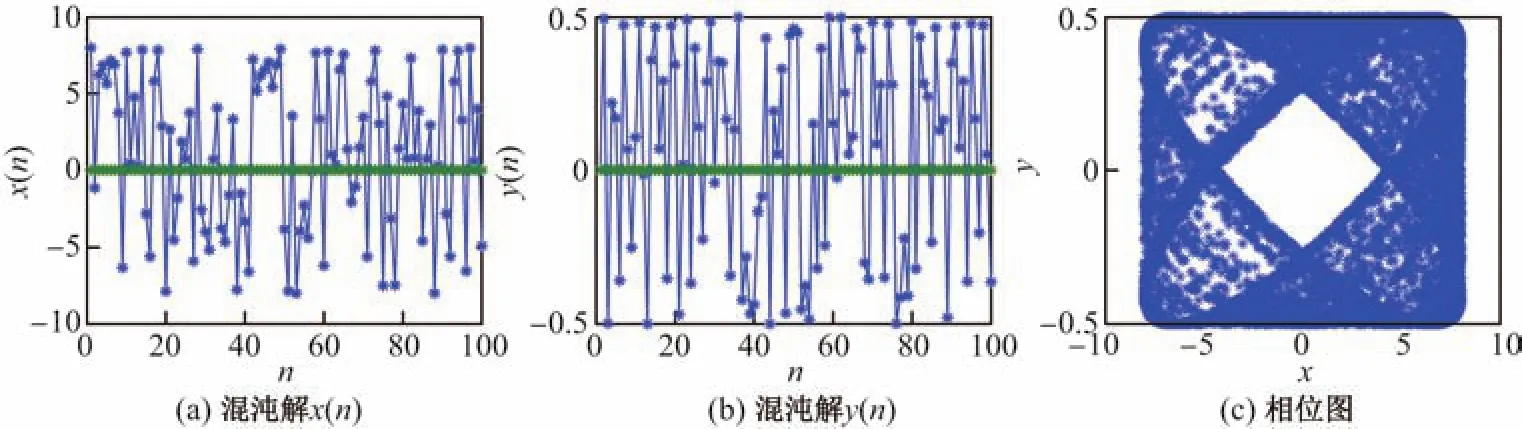
图 3 ν=0.999时系统(5)中的混沌Fig.3 Chaos in system(5)when ν=0.999

图 4 ν=0.900时系统(5)中的混沌Fig.4 Chaos in system(5)when ν=0.900

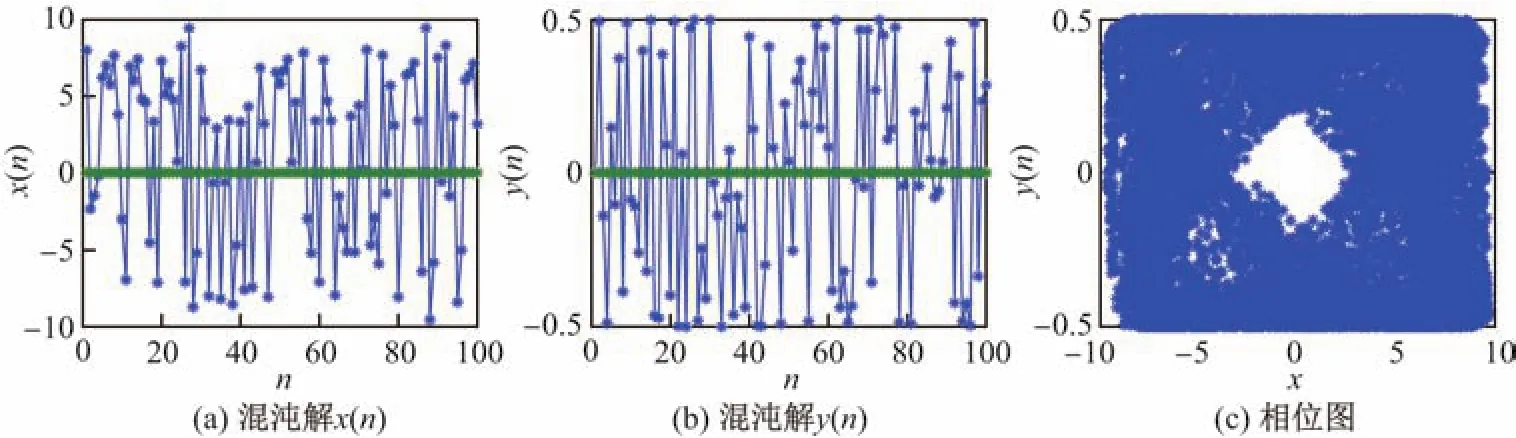
图 5 ν=0.850时系统(5)中的混沌Fig.5 Chaos in system(5)when ν=0.850

5 结束语

分数阶差分是生成分数阶离散映射的一个有效工具,本工作就是利用分数阶差分,在一个离散混沌系统的基础上,生成了一个分数阶的离散混沌系统.比较原系统及新系统在不同分数阶下的相位图可以直观地看到,0<ν<1的系统是原系统的扩展.此外,值得一提的是,分数阶的离散混沌系统在图像信息隐藏方面具有很好的应用.