非共振耗散腔耦合系统的发射光谱

张 杨，吕树臣

(哈尔滨师范大学 光电带隙材料教育部重点实验室，黑龙江 哈尔滨 150025)

1 引 言

腔量子电动力学(Cavity quantum electrodynamics)主要研究受限空间中的电磁场与物质(主要有原子、离子以及量子点等)间相互作用的动力学过程[1]，并且为研究各种量子现象提供了一种自然的环境[2]。在腔量子电动力学中，腔内的原子系统可以作为存储量子位，而光子可以在整个系统中分布信息[2]。因此，腔量子电动力学的研究对于量子通信[3]、量子信息处理[4]、量子计算[5]、量子纠缠[6]等领域有重要意义。在研究单个理想二能级原子与单模腔场相互作用的Jaynes-Cummings(简称J-C)模型[7]建立以后，人们对原子和腔场相互作用过程的本质进行了很多研究，并且发现许多量子现象，如辐射光场的压缩效应[8]、光场的真空拉比分裂[9]、辐射光谱的坍缩和复起[10]、J-C模型中的非线性[11]、光子的反群聚和亚泊松分布[12]等。随着研究的深入，模型推广到了两个二能级原子与单模腔场相互作用的Tavis-Cummings(简称T-C)模型[13]。

由于腔场谱和原子发射谱是获取原子和腔场相互作用信息的重要手段[14]，并被实验所证实[15-16]。因此，发射光谱的研究一直备受重视，人们研究了单个二能级原子与高品质因子单模腔场相互作用的发射光谱[17]、单个二能级原子与单模腔场双光子发射光谱[18]、两个二能级原子与单模腔场在强耦合机制下相互作用的透射谱[19]以及两个二能级原子与单模光场在偶极子相互作用影响下的发射光谱[20]。近年来，双原子与双单模腔耦合系统模型也受到了人们的广泛关注，Zhang 等[21]讨论了双原子与双单模腔系统的量子态转移，Wang等[22]研究了驱动情况下双原子与双单模腔的光子分布，Ferretti等[23]研究了双原子与双单模腔在相干驱动和耗散下的光子相关性。

随着实验技术的发展，实验上能够实现量子点与半导体腔的耦合[24]，也能实现量子点与光子晶体腔的耦合[25]，实验上能观测到量子点与腔耦合的Mollow三重峰[26-27]，并对解释中峰的出现产生了极大的兴趣，然而，目前关于中峰出现的解释说法不一[28]。本文目的之一就是根据我们的研究结果对中峰的出现给出解释。

到目前为止，有关双原子与双单模腔场相互作用系统发射光谱的相关报道很少。因此，本文将研究双原子与双单模腔场相互作用系统的发射光谱，着重讨论腔场与原子失谐、原子与腔场失谐、腔场衰减率以及原子的失相对发射光谱的影响。

2 腔耦合系统模型

本文在以往模型研究的基础上，即两个单模腔彼此相互耦合，每一个腔中都有一个二能级原子(或量子点)[29-30]，考虑了腔1由于光子渗漏造成的腔场衰减，腔2受到非相干泵浦及两个原子的失相，研究模型如图1所示。每个腔中原子与该腔场在偶极作用近似下，其耦合强度为Ωi(i=1,2)，两个单模腔场间通过偶极-偶极相互作用，其光子隧穿强度为J。这里不考虑两个原子间的相互作用，以及原子与相邻腔场间的相互作用。

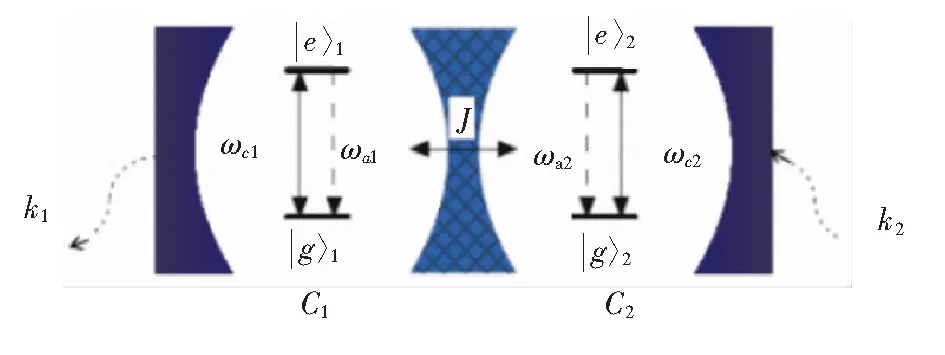
图1 二能级双原子与双单模腔耦合系统模型

Fig.1 Two double-level atoms coupled with two single-mode cavity system

该体系的Hamiltonian在旋波近似(RWA)和电偶极近似下可表示为(ћ=1)：

H=H0+H1,

(1)

其中

(2)

(3)

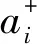
考虑到腔衰减、纯失相、非相干泵浦等因素的影响，这种耦合原子-腔系统的演化在玻恩-马尔可夫近似下可以用量子耗散主方程来描述，此时耦合体系的量子主方程可写为[28]：

(4)

其中，κ1为腔场1的衰减率，κ2为腔场2的非相干泵浦率，γ*为原子的失相。

对本文考虑的模型，第二个腔引进非相干泵浦，通过两个腔的耦合，使得这个非相干泵浦去平衡第一个腔的衰减，从而使整个系统能建立起一种稳态，这样系统的初始条件不需要人为设定。由公式(4)，利用单光子关联近似[31]〈σza〉=-〈a〉及Bose统计，我们得到如下方程组：

(5)

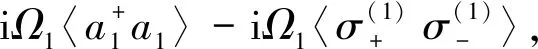
(6)

(7)

(8)

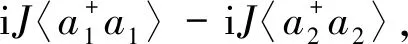
(9)

(10)

(11)

(12)

(13)

(14)

令方程组(5)～(14)的时间导数为零，可得到平均值的稳态解，如

(15)

(16)

(17)

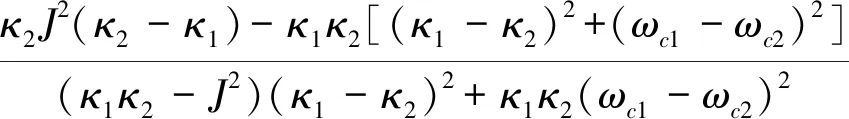
(18)

(19)

(20)

根据Wiener-Khintchine定理，该系统的发射光谱可按下式计算：

(21)

(22)

3 耦合系统的发射光谱

下面分别讨论腔场与原子失谐Δca=ωc-ωa、原子与腔场失谐Δac=ωa-ωc、腔场衰减率κ1以及原子失相γ*对该体系发射光谱的影响，并将原子发射谱和腔场谱进行了对比分析。取定腔场的固有频率ω0=1014Hz，原子的跃迁频率和腔场的跃迁频率均与固有频率有相同的数量级。腔场的衰减率、腔场的非相干泵浦率、失相分别为κ1=κ2=γ*≈109Hz。原子和腔场间耦合强度、两腔场间耦合强度分别取为Ω1=Ω2=J≈1010Hz。在本文研究过程中取定ωci/Ω1=ωai/Ω1=10 000(i=1,2),J/Ω1=1.8,Ω1/Ω1=1，κ1/Ω1=0.5,κ2/Ω1=0.1,以及γ*/Ω1=0.1。

3.1 腔场与原子失谐影响下的谱结构

图2给出了耦合系统的腔场谱及原子发射光谱随腔场与原子失谐Δca/Ω1=(ωc1-ωa1)/Ω1的变化关系。保持其他参量不变，只改变ωc1，使Δca/Ω1=-2,-1,0,1,2。结果表明：腔场谱谱线有3个发射峰，如图2(a)所示，原子发射谱谱线有两个发射峰，如图2(b)所示。从图2(a)可以看出腔场谱当且仅当Δca=0，即共振时，谱线表现为对称性，而其余失谐情况均为非对称峰，并且随着失谐的增大，两边峰向低频段漂移，中峰的位置固定不变(位于ω=ω0处)。

共振情况下，不仅腔场谱的谱线对称，原子发射谱的谱线也对称，且腔场谱的峰位比原子发射谱的峰位偏移中心位置更多一些。失谐情况下，腔场谱和原子发射谱位于高频段峰位差变小，位于低频段腔场谱和原子发射谱峰位差变大。

在腔场谱中，如图2(a)所示,位于高频段边峰的光谱强度随着腔场与原子正失谐的增大而增大；随着腔场与原子负失谐的增大而逐渐减小；位于低频段的边峰光谱强度的变化刚好相反，而失谐的变化对中间峰位的光谱强度几乎无影响。在原子发射谱中，如图2(b)所示，位于高频段的发射强度随着腔场与原子失谐的增大在逐渐增大；位于低频段的发射强度随着腔场与原子失谐的增大而逐渐减小。对于同一失谐影响下的两个边峰，光谱强度变化规律相似，即其中任一边峰在腔场谱中光谱强度大(小)，在原子发射谱中的光谱强度也大(小)。

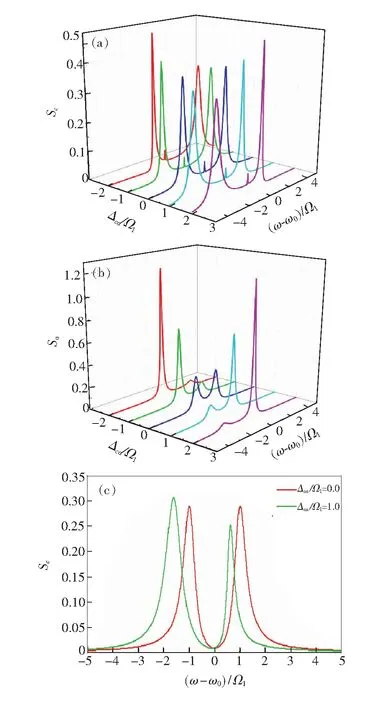
图2 腔场与原子失谐影响下，(a)腔场谱的变化关系；(b)原子发射谱的变化关系；(c)两腔场间耦合强度为零时腔场谱的变化关系。

Fig.2 Under the influence of the detuning between the cavity field and atom: (a) change of cavity field spectra; (b) change of atomic emission spectra; (c) change of cavity field spectrum when the coupling strength between two cavity fields is zero.

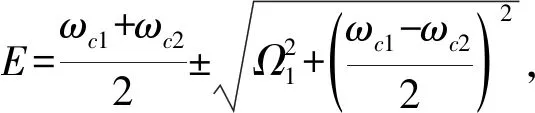
在讨论单腔模与二能级单原子耦合系统中，无论在理论还是实验上，都发现了Mollow三重峰的存在[27,32]。一个令人特别感兴趣且迷惑的现象是解释中峰的出现，在以往的报道中，Mollow三重峰的出现要么与外加泵浦场相关[27]，要么与声子耦合相关[33-34]。从我们的研究结果可以得出这样的结论：只要单腔模与二能级单原子耦合系统受到外界相干场的作用，理论上就应出现Mollow三重峰，例如在本文所研究的系统中，由于腔间耦合的存在(J≠0)，由方程(19)和(21)不难看出腔1发射谱Mollow三重峰必然存在(当然不排除有两个峰重叠的情况)。

3.2 原子与腔场失谐影响下的谱结构

图3阐述了耦合系统的腔场谱及原子发射光谱随原子与腔场失谐Δac/Ω1=(ωa1-ωc1)Ω1的变化关系。在保持其他参量不变的情况下，只改变ωa1，使Δac/Ω1=-2,-1,0,1,2。由图3(a)不难发现，在失谐的情况下，随着Δac的增加，腔场谱中峰的强度明显增大，且中峰峰位明显偏离ω=ω0的位置，从高频向低频移动。特别是，中峰的强度关于Δac=0呈对称性增长。

在腔场谱中，如图3(a)所示，高频段的光谱强度随着原子与腔场正失谐的增大而增大；随着原子与腔场负失谐的增大而逐渐减小；低频段的边峰光谱强度的变化刚好相反。对原子发射谱而言，如图3(b)所示，位于高频段的光谱强度随着Δac的增大而减小；位于低频段的光谱强度随着Δac的增大而增大。图2(b)和图3(b)均表明当原子与腔场负失谐时，低频侧发射谱强度弱于高频侧发射谱强度，当原子与腔场正失谐时，低频侧发射谱强度大于高频侧发射谱强度。

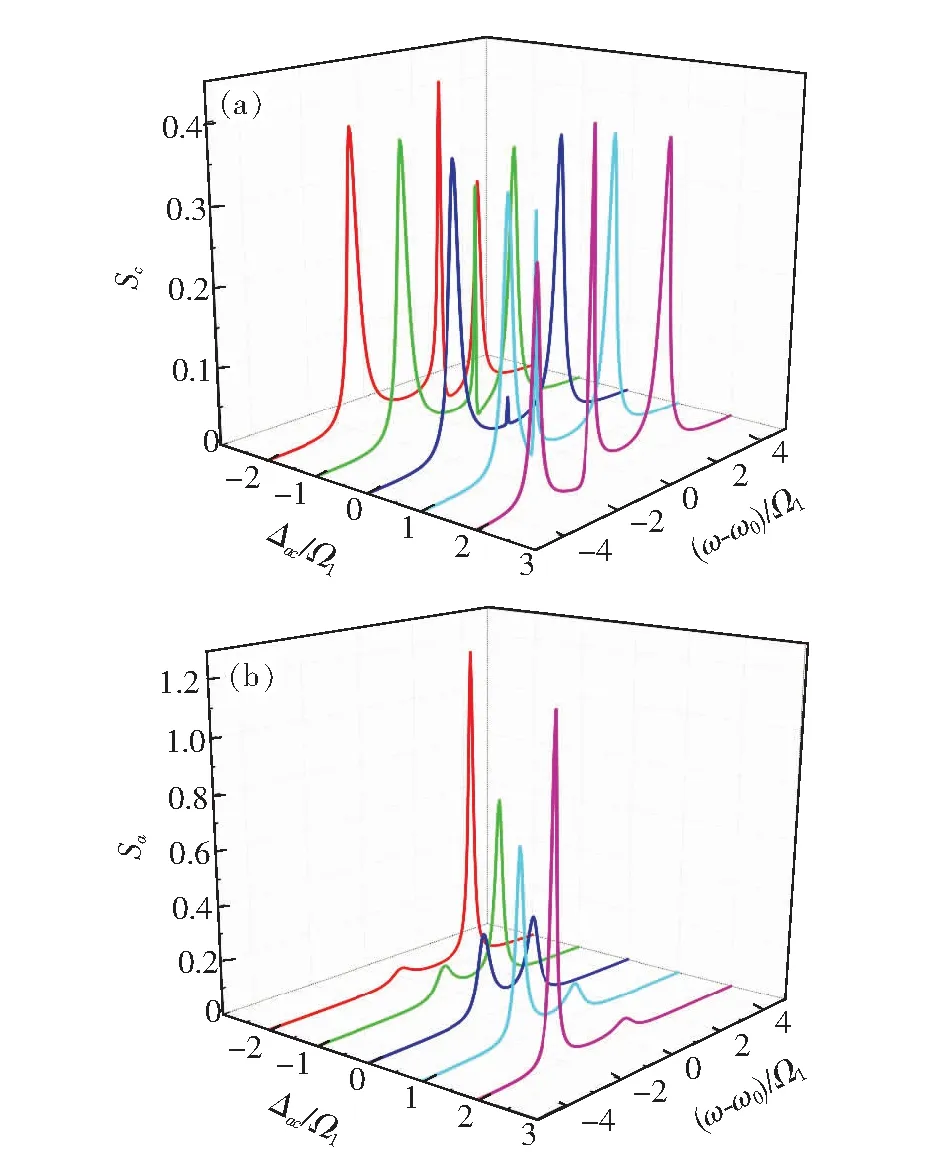
图3 原子与腔场失谐影响下，(a)腔场谱的变化关系；(b)原子发射谱的变化关系。

Fig.3 Under the influence of the detuning between the atom and the cavity field: (a) change of cavity field spectra; (b) change of atomic emission spectra.

3.3 腔场衰减率影响下的谱结构

图4为共振情况时，耦合系统的腔场谱及原子发射光谱随腔场衰减率κ1的变化关系。保持其他参量不变，κ1/Ω1=0.5，0.6，0.7，0.8。从图4(a)可以看出，随着腔场衰减率的增大，腔场谱3个峰的峰位均无变化，两个边峰的强度均逐渐降低，且降低的幅度也在逐渐减小，两边峰谱线的线宽变得宽化。对应于同一腔场衰减率，腔场谱两边峰的强度相同，如图4(a)所示。

对于原子发射谱来说，随着腔场衰减率的增加，两个峰的强度也在减小，两个峰的峰位均有向内微弱的移动，谱线的线宽均向内宽化；对应于同一腔场衰减率，原子发射谱两边峰的强度也是相同的，如图4(b)所示。 在本文所研究的模型中，虽然我们未考虑原子的自发辐射(即原子发射的衰减率)对原子发射谱带来的影响，但从方程(20)可以推断腔场衰减率通过腔场与原子的耦合作用，间接影响到原子发射谱的发射强度，这一推断为图4(b)所证实。

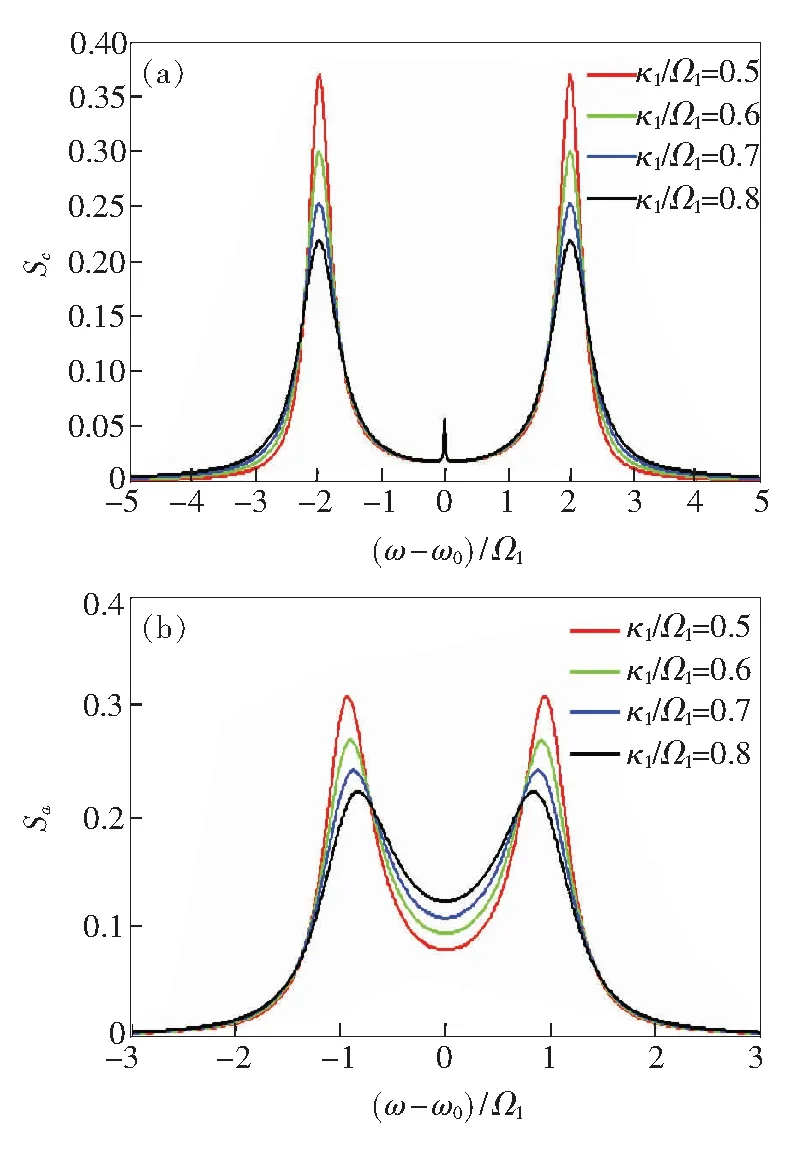
图4 共振时，腔场衰减率影响下，(a)腔场谱的变化关系；(b)原子发射谱的变化关系。

Fig.4 Under the influence of cavity decay rate in the case of resonance: (a) change of cavity field spectra; (b) change of atomic emission spectra.

图5为失谐情况时，耦合系统的腔场谱及原子发射光谱随腔场衰减率κ1的变化关系。保持其他参量不变的情况下，取定ωa1/Ω1=9 998，κ1/Ω1=0.5，0.6，0.7，0.8。从图5(a)可以看出，对于腔场谱来说，失谐时，对应于同一腔场衰减率，中峰光谱强度最大，低频段边峰的光谱强度大于高频段边峰的光谱强度。随着腔场衰减率的增大，3个峰的强度均逐渐降低，且降低的幅度均逐渐减小，中峰衰减的幅度最大，其次是低频段边峰，最后是高频段边峰；中峰和低频段边峰的峰位均无明显变化，而高频段边峰向低频侧有微弱的移动。此外，3个峰谱线的线宽变得宽化，如图5(a)所示。

对于原子发射谱来说，失谐时，对应于同一腔场衰减率，高频段边峰的光谱强度大于低频段边峰的光谱强度。随着腔场衰减率的增加，两个峰的强度均在减少，高频段边峰衰减的幅度大于低频段边峰衰减的幅度；两个峰的峰位无明显变化，谱线的线宽变得宽化，如图5(b)所示。随着κ1的增大，对于腔场谱来说衰减的幅度大于原子发射谱，说明作用在腔场上的衰减率对腔场谱的影响更大一些，这是因为腔场的衰减率通过原子和腔场耦合间接地影响原子发射谱。

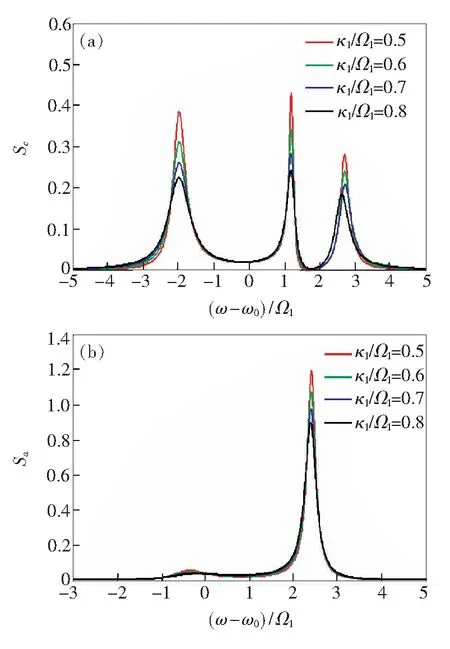
图5 失谐时，腔场衰减率影响下，(a)腔场谱的变化关系；(b)原子发射谱的变化关系。

Fig.5 Under the influence of cavity decay rate in the case of detuning: (a) change of cavity field spectrua; (b) change of atomic emission spectra.

3.4 原子失相影响下的谱结构

图6为共振情况时，耦合系统的腔场谱及原子发射光谱随原子的失相γ*的变化关系。保持其他参量不变，γ*/Ω1=0.1，0.2，0.3,0.4。随着γ*的增大，边峰均逐渐降低，而且降低的幅度逐渐减小，对于腔场谱来说衰减的幅度小于原子发射谱，说明作用在原子上的失相对原子发射谱的影响更大一些，这是因为原子的失相通过原子和腔场耦合间接地影响腔场谱。对应于同一失相下，腔场谱中边峰的强度相同，原子发射谱两个峰的强度也相同。

在腔场谱中，如图6(a)所示，随着失相的增大中峰的强度逐渐减小，但减小的幅度非常小。随着失相的增加，谱线的线宽向内宽化。在原子发射谱中，如图6(b)所示，随着失相的增大，两个峰的位置均有向外微弱的移动，谱线线宽均向外宽化。原子的失相导致发射光谱强度降低和谱线宽化，这与文献[35]考虑失相的单模腔与单原子耦合系统得到的结论是一致的。

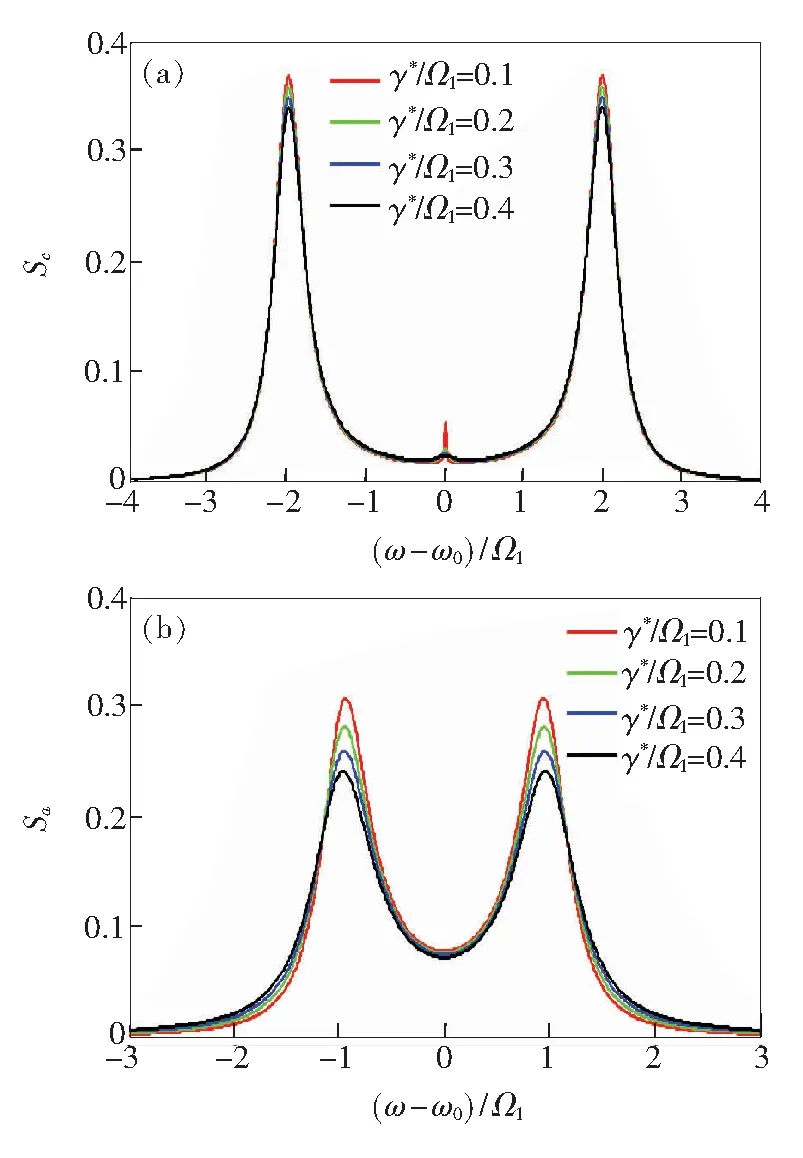
图6 共振时，原子失相影响下，(a)腔场谱的变化关系；(b)原子发射谱的变化关系。

Fig.6 Under the influence of atom dephasing in the case of resonance: (a) change of cavity field spectra; (b) change of atomic emission spectra.

图7为失谐情况时，耦合系统的腔场谱及原子发射光谱随原子的失相γ*的变化关系。保持其他参量不变的情况下，取定ωa1/Ω1=9 998，γ*/Ω1=0.1，0.2，0.3,0.4。从图7(a)可以看出，对于腔场谱来说，失谐时，对应于同一原子失相，中峰的光谱强度最大，低频段边峰的光谱强度大于高频段边峰的光谱强度。随着腔场衰减率的增大，3个峰的强度均逐渐降低，且降低的幅度均逐渐减小，中峰衰减的幅度最大，其次是低频段边峰，最后是高频段边峰；3个峰的峰位均无明显变化。此外，3个峰谱线的线宽变得宽化。

对于原子发射谱来说，失谐时，对应于同一腔场衰减率，高频段边峰的光谱强度大于低频段边峰的光谱强度。随着腔场衰减率的增加，高频段边峰衰减的幅度明显；而两个峰的峰位无明显变化，谱线的线宽变得宽化，如图7(b)所示。随着γ*的增大，对于腔场谱来说衰减的幅度小于原子发射谱，说明作用在原子上的失相对原子发射谱的影响更大一些，对腔场谱的影响小一些，这是因为原子的失相通过原子和腔场耦合间接地影响腔场谱。

图7 失谐时，原子失相影响下，(a)腔场谱的变化关系；(b)原子发射谱的变化关系。

Fig.7 Under the influence of atom dephasing in the case of detuning: (a) change of cavity field spectra; (b) change of atomic emission spectra.

4 结 论

本文研究了二能级双原子与双单模腔耦合系统的发射光谱。我们发现腔场与原子失谐和原子与腔场失谐对发射谱有着不同的影响，腔场与原子失谐的增大可使边峰向低频段漂移，并改变其光谱强度；原子与腔场失谐的增大可使光谱整体向低频段漂移，并改变其光谱强度。随着腔场衰减率的增大或失相的增大，耦合系统边峰的强度减小，并且宽化。本文的研究结果可以例证：单腔模与二能级单原子耦合系统受到外界相干场的作用，理论上就应出现Mollow三重峰。