基于Hoek-Brown大坝非饱和岩质边坡安全稳定系数推导

王 楠

（国网湖北省电力有限公司电力科学研究院，武汉 430077）

1 概述

边坡在降雨条件下失稳的例子屡见不鲜[1-2]，降雨会导致边坡的下滑力增加，加剧边坡失稳[3-4]；边坡内部地下水位升高，岩体的有效应力、岩体的强度参数因而减小[5-6]，从而导致边坡失稳现象的发生。边坡失稳的危害主要体现在： 对边坡所在地区的建筑物造成破坏； 对灾区周围的剧名的生命财产安全造成威胁[7]。因此，对边坡稳定性的研究显得十分必要和迫切。

针对土质边坡的研究较多，但对于岩质边坡在降雨条件下的稳定性分析相对较少，Hoek E.和Brown E.T在1980年[8-9]结合岩石性状方面的理论研究和实践经验，本文基于Griffith的脆性断裂理论，提出了岩石强度准则：Hoek-Brown强度准则，可以综合考虑岩体的各方面特性[10]，因此，本文推导了一种基于Hoek-Brown准则。

2 计算理论

考虑岩体非饱和特性的极限平衡安全系数，结合一典型边坡在降雨条件下的边坡渗透稳定性规律，为降雨条件下的岩质边坡稳定性规律提供参考。

2.1 渗流基本方程

非饱和渗流的控制方程写成张量的形式为：

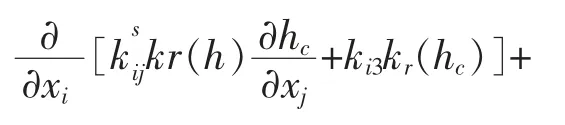
式中 xi，xj为位置标识；t为时间变量；kr为相对透水率（m/d）；kij为饱和渗透张量（m/d）；hc为压力水头（m）；Q为总流量（m3）；C（hc）为容水度（m3/m3）；θ为压力水头函数；n为孔隙率；Ss为单位贮水量。

2.2 基于Hoek-Brown准则强度参数推导

Hoek-Broown准则的主应力[8-9]可表示为：

式中σ1和σ3为大小主应力（MPa）；σc为材料强度（MPa）；mb为岩体特性参数，为岩体性状参数；GSI为地质指标；D为岩体损伤因子参数。s可表达为：；α可写成以下形式：α=0.5+（e-GSI/15-e-20/3）

运用Mohr-Coulomb准则表达Hoek-Brown准则。

φ为内摩擦角度（°）；σ1=kσ3+b，k为斜率，k=1+b为主应力轴交点纵坐标，

Mohr-Coulomb准则下的c，φ值可写为：

2.3 考虑非饱和Hoek-Brown抗剪强度推导

非饱和抗剪强度[11]，可写为：

式中 τf为岩体抗剪强度 （MPa）；c，φ为有效强度参数；σ为法应力（kN）；ua为气压力（MPa）；uw为水压力（MPa）；φb为负孔压参数。

基于Hoek-Brown推导非饱和强度，其公式可写为：

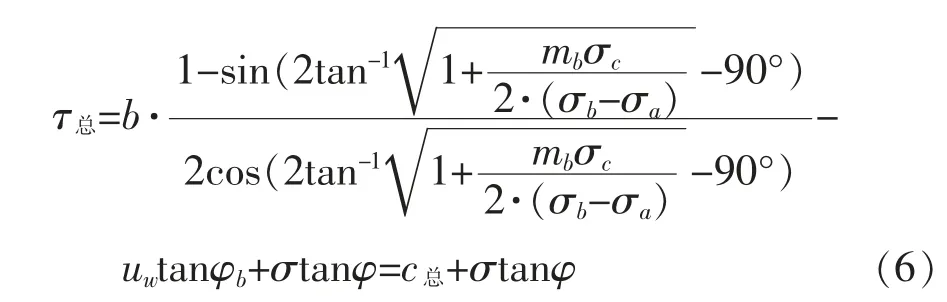
式中 τ总为抗剪强度（MPa）；c总为黏聚力。强度参数均考虑了非饱和特性及Hoek-Brown准则。

2.4 基于Hoek-Brown准则非饱和安全系数

安全系数公式可表示为：

式中 FS为安全稳定系数；c总为黏聚力；β是底边长（m）；W为土条重；α为倾斜角（°）；φ为内摩擦角（°）；mα为岩体状态参数：

3 计算模型

3.1 计算模型及边界条件

本文选取边坡计算模型如图1，坡度45°，如图1（a）3个监测面（上部、中部及下部监测面）来实时监测在降雨下的边坡内部孔隙水压力。以图1（a）初始地下水位线计算渗流场作为初始条件，边界条件设置如下：

（1）ah，gf为零流量边界。

（2）bcde为降雨边界，当降雨强度大于岩体的渗透系数时，入渗强度等于岩体的渗透系数，当降雨强度小于岩体的渗透系数时，入渗强度等于降雨强度。

（3）ab，ef，hg视为不透水的零流量边界。

模型网格如图1（b），共剖分3831个单元，3907个节点。

图1 计算模型

3.2 计算参数

饱和渗透系数取ksat=0.1m/d，重度γ=26kN/m3，边坡土的土水特征曲线如图2，岩体的基础Hoek-Brown参数为σc=170kPa，mi=14，GSI=65，D=0.6，降雨类型选取典型的平均型降雨，降雨总量1000mm，降雨时长10d，同时考虑停雨5d的情况。

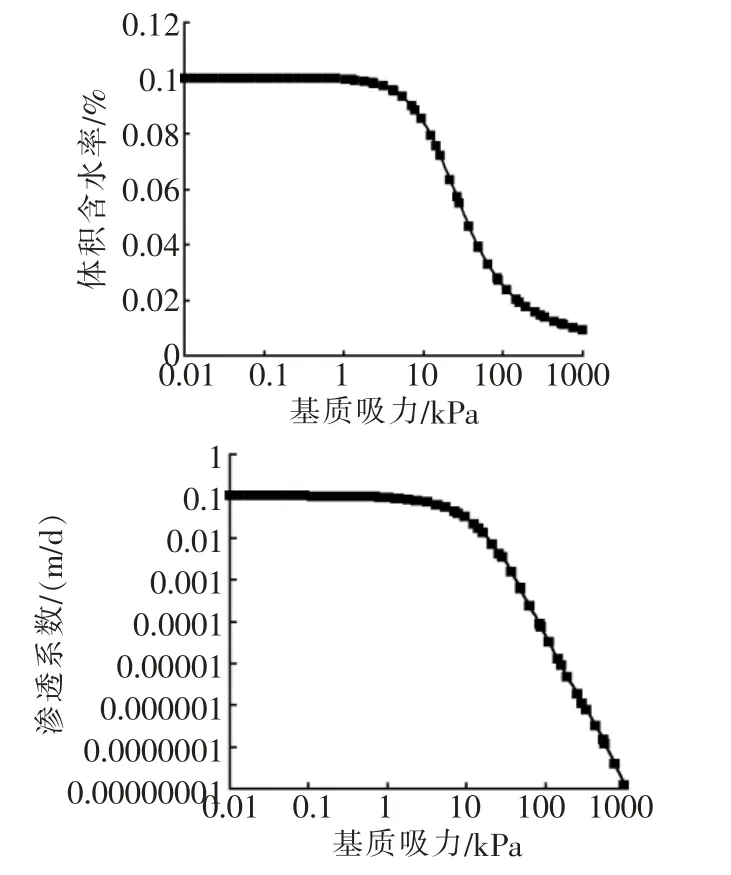
图2 土水特征曲线

4 计算结果

4.1 孔压变化分析

平均型降雨条件下的边坡上部监测面，中部监测面及下部监测面的孔压变化规律如图3。

由图3发现以下规律：

（1）上部监测面孔压在降雨时深度为6m以上的岩体中的孔压变化较大，而在6m以下即深层的孔压变化并不大，在停雨后表层孔压迅速降低，深层孔压继续增大。

图3 平均降雨孔压变化

（2）中部监测面孔压在降雨时深度为2m以上的岩体中孔压变化较大，而在深度为2m以下的孔压随降雨的增大而逐渐增大，当停雨后岩体表层的孔压略有下降，而岩体深层的孔压则略有上升。

（3）下部监测面孔压随深度呈现线性增大的规律，在降雨过程中孔压整体上呈现整体增大的趋势，而在停雨后则呈现整体略微减小的规律。

4.2 体积含水率变化

平均型降雨条件下的边坡上部、中部及下部监测面的体积含水率变化规律如图4。

图4 平均型降雨体积含水率变化

由图4可见，平均型降雨条件下不同监测面的体积含水率变化规律如下。

（1）上部监测面体积含水率在深度12m以上的部分体积含水率变化较大，总体规律呈现在降雨过程中体积含水率由浅部首先升高，而后逐渐向深部发展，而在降雨结束后则慢慢降低，在深度12m以下的部分体积含水率则不变（基本处于饱和状态）。

（2）中部监测面体积含水率在深度为8m以上的部分体积含水率随降雨的过程变化较大，在降雨过程中岩体表层的体积含水率迅速增大，在停雨后体积含水率则慢慢减小，而在深度为8m以下的部分体积含水率保持为饱和状态不变。

（3）下部监测面体积含水率变化与上部与中部监测面的规律略有不同，在深度为5m以上体积含水率变化较大，且随降雨呈现整体的体积含水率的上升，降雨结束后则整体达到饱和，而在停雨后则几乎保持不变，与上部监测点与中部监测点的规律差异较大，究其原因，是因为边坡下部受到上部与中部地下水的排泄所造成。

4.3 安全系数变化规律

平均型降雨条件下的边坡安全系数变化规律如图5。

图5 安全系数变化

由图5可见，安全系数在降雨时逐渐减小，减小的规律呈现“先加速，后缓慢，再加速，最后稳定回升”的规律。

5 结语

（1）不同监测面孔压变化较大的深度分别是上部监测面6m，中部监测面2m，下部监测面0m，降雨开始时刻表层孔压迅速增大，而结束时缓慢减小。

（2）不同监测面的体积含水率变化较大的深度分别为上部监测面12m，中部监测面8m，下部监测面5m，上部监测面与中部监测面在降雨时刻表层体积含水率迅速增大，在体积含水率结束后体积含水率则缓慢减小，下部监测面在降雨时刻体积含水率整体增大，而降雨结束后保持不变。

（3）安全系数变化呈现“先加速，后缓慢，再加速，最后稳定回升”的规律。