广义的戈登—舍费尔最优收获策略随机变化环境中的模型
杨小平,唐三一
(1. 陕西交通职业技术学院 基础部,陕西 西安 710018; 2. 陕西师范大学 数学与信息科学学院,陕西 西安 710062)
在估计种群的大小及其对捕捞的反应,预测未来的成功以及选择适当的战略以维持稳定的可持续量和保持健康的种群是管理渔业最具挑战性和最重要的问题,这些问题在很大程度上都是与系统的静态行为有关,从某种意义上说,人口涉及到平均产量(或平均收入)的估计,他是开发水平的函数[1],此外,由于自然种群对其物理生物环境的随机扰动有波动的倾向,管理问题变得复杂。一些研究人员已经调查了在随机波动的环境中收获种群的情况[2-4]。已经观察到,人口对这种随机扰动的敏感性取决于其重要比率(生育率、死亡率和补充率),因此,一般来说,收获是改变的。如果不小心收获超过了最大可持续产量(MSY),这些影响就会变得非常严重。高的努力可能导致低平均产量和高方差。Schaefer[5]基于罗蒂斯克定律和Reed[6]和Goh[7]的鱼类收获动态开放存取模型也考虑了在无限时间范围内收获种群的罗蒂斯克增长率。本文提出并研究了一种随机修正的罗蒂斯克模型。该模型适用于水库产生的倍增波动情况下的鱼类捕捞,我们的模型包括戈登—舍费尔模型和佩拉—汤姆林森模型[8]。
1 模 型
让n(t)表示在时间t的库存大小;处理n(t)是一个连续变量(考虑到库存的大小是合理的),用于鱼类收获的戈登—舍费尔模型有微分方程描述:

(1-1)
=f(n)-h(t)
(1-2)
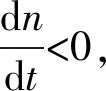

(2)
其中V(t)是一个白噪声过程,表示随机微分方程SDE式(2)[9-10]可以写成:

(3)
其中W(t)是一个维纳过程,其形式导数是过程V(t)。
2 模型的确定性分析
Holt[11]之后,我们的标准化状态变量n(t)化为φ(t),未利用的平均值的一部分,此外,还强加了霍尔特的约束:①未开发库存水平的1/2用于征聘,是为未开发库存水平的3/4;②自然死亡率系数是统一的,我们发现我们的随机微分方程式(3)化简为:
dφ=[rφ(1-φα-1)-Eφ]dt+σφdW
(4)
r是内在增长率,这是关于α的函数:

(5)
可持续产量是:
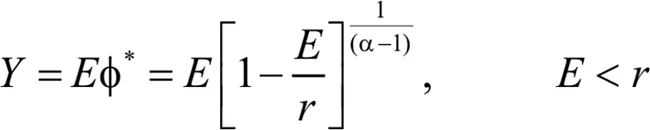
(6)
其中φ*是式(1-1)非零平衡解和发生在E=E*=r(1-1/α)上的MSY是由:
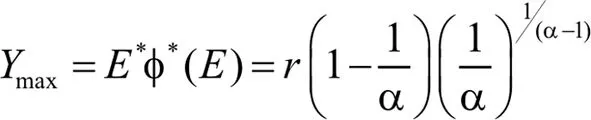
(7)
更进一步的可以看出MSY,Ymax是渐进稳定的,因为每当有小的扰动,随着时间的推移,Ymax就会恢复。

(8)
因为由一点代数计算就能得到:

(9)
在α>1,r>0,Y的渐进稳定性由式(9)得到。
2.1 可持续的产量与努力
α的各种值的计算表明,对于α=2,Ymax=0.25是在努力水平E*=0.50达到的,当α超过2并且逐渐增加时,产量与努力曲线的峰值的位置向左移动,而当α减少到2以下时,产量与努力曲线的峰值向前移动。
正如我们在介绍中提到的α=2、3、4时,我们的模型可以减少,模型分别由舍费尔和佩尔—汤姆林森(m=2,3)建立,特别地,Lett和Doubleday[12]研究表明:反向峰值佩尔—汤姆林森曲线比罗辑分析更能描述圣劳伦斯鳕鱼湾的大量数据。这一发现至少在一定程度上表明,我们的模型实际上是一个扩展。
值得注意的是,当α向α=2的右边移动,所需的努力水平E*降低,而最大可持续产量Ymax增加,因此相对于α>2与α≤2相比较,该物种的收获更有利可图(见表1)。r=r(α)的值,使可持续产量φ*(E*)最大化的努力水平E*,当E=E*时φ的平衡值和最大持续产量Ymax=Y(E*,φ*(E*))显示不同的α值。

表1 α取不同值时φ的平衡值及最大可持续产量对比
2.2 收获库存的特征回归时间TR
到目前为止,我们已经研究了库存φ和可持续产量Y的依赖性,在收获状态下,在稳定状态下。在这一节中,我们将研究动态方面,解决的基本问题是,当受到均衡价值的影响时,开发会如何影响库存趋于恢复的速度,对于一个微分方程组描述的模型,他的特征时间TR由其Hession矩阵的主特征值的实部的幅度(绝对值)的倒数给出,如果所有特征值位于复平面图的左半部分。因此,原始种群的特征时间为TR(0),收获种群的特征时间为TR(E),结果是:

(10)
和

(11)
其中的r(α),任意的α是由式(5)给出的。
因此,

(12)
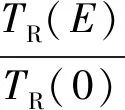
2.3 时间平稳收获策略的随机分析
在本节中,我们将对随机微分方程式(4)描述的收获模型进行随机分析,但需满足以下条件:①时间视界是无限的,没有任何折现因子;②环境中普通存在的波动是倍增的,是由白噪声过程产生的;③我们的吸引力和直观的收获政策是对于某些临界规模的nc(根据经验确定)在n(t)>nc的情况下进行收获,当n(t) 正如Abakuks和Prajneshu[13]以及Shah[14]所展示那样,我们的模型甚至可以证明时间平稳的政策导致了最大的长期效益。 保持这些建议,继续规范化鱼群φ(t)=n(t)/K,我们的模型式(4)化简为: dφ=[rφ{1-φα-1}-EφH{φ(t)-φc}]dt+σφdW(t) (13) 其中H(x)是赫维赛德函数,定义为: (14) 将给出漂移和扩散项: (15) 和S(φ,t)=σ2φ2 (16) 对应于随机微分方程式(13)的相关的福克——普朗克方程为: (17) 在稳定状态下减少到: (18-1) (18-2) 积分(18-1)和(18-2),我们得到: (19) 其中A和B是积分常数,并由连续性条件确定。 (20) 和归一化条件: (21) 我们得到: (22) 其中γ(v,u)和Γ(v,u)是不完全伽马函数。 给定临界尺寸φc的长期收益由: (23) 最后,将B的值代入式(23)并化简,我们发现: (24) 对于给定的φc,另一个感兴趣的数量在长期的时间比例T(φc)是用于收获: (25) 我们提出并研究了戈登—舍费尔模型咋随机波动环境下鱼群收获的推广,从而产生了乘性噪声,我们的模型包括梅等人讨论的3个重要模型。我们用一般的 作为泛化指标,生长速率曲线因物种而异。结果表明: 对于生长速率曲线发展较快的物种来说是一个更好的选择; 值给出了增长缓慢的曲线我们研究了与鱼类捕捞有关的若干因素的依赖性。如最大可持续产量、特征回归时间、长期平均产量、长期时间比例等,这有助于渔业管理。

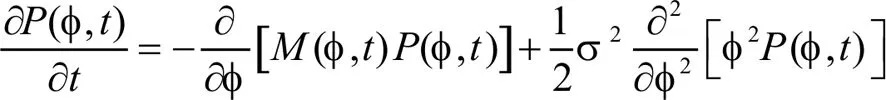
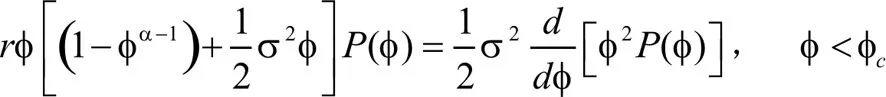
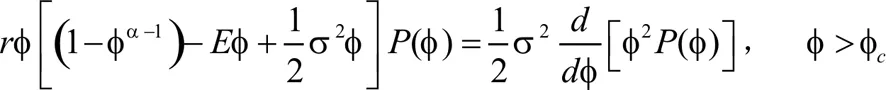






3 结 语

