NEAR模型的外墙面裂缝连接算法

吴生宇,李明心,林靖宇

(广西大学 电气工程学院,南宁 530004)

1 引 言

随着高层乃至超高层建筑物的建成[1],随之而来的高层建筑物养护和安全保障等问题也变得越来越重要.在实际的工程中,建筑物外墙面检测也是在慢慢的从人工到半自动化发展的,从最开始的使用固定吊绳近距离检测到远距离固定位置红外技术检测.为了方便快捷的检测需求,不断地提出新的方法思路并在实际应用和实践中加以改善.高层建筑物外墙面检测目前通用的方法还是通过人工观察的方式来完成,其效率低,速度慢,存在很大的问题,很难适应高层建筑安全保障现代化的发展需求.因此,高层建筑物外墙面检测技术要求从人工检测向智能自动化检测方向发展.

目前基于图像的裂缝自动检测算法,大多应用在检测路面裂缝及其桥梁裂缝方面,而应用在墙面检测方面较少.国内外许多相关领域的学者进行了大量研究,提出了多种裂缝检测算法和理论.关于裂缝的检测算法大致分为4类:1)基于几何分析的方法[2];2)基于分块分析的方法[3];3)基于灰度统计的方法[4];4)基于边缘检测的方法[5];这些算法对裂缝检测时取得了较好的效果,但是在用这些算法检测裂缝时,由于部分裂缝过窄或被灰尘填充或在预处理过程中产生的裂缝断裂,导致检测出的裂缝目标不连续,而这些方法没有对裂缝进行连接,或者只是直接对相邻裂缝的邻近端点连接,如K-D树[6]连接算法,连接效果不佳,并未表达出真实裂缝的完整骨架结构,严重影响后续的裂缝参数测量和评估.

建筑物表面图像的获取是进行建筑物外墙裂缝危害检测的第一步,是后续所有工作的基础.建筑物越大,获取完整的表面图像需要花费越多的时间,而且越高的建筑物,对于建筑物表面图像的获取越不容易.爬行机器人[7]、无人机[8]等几种是目前较新的图像获取技术,这些技术解决了传统建筑物外墙图像获取的效率低、危险性大等问题.J.P.Zavala De Paz等人[9]设计了一款带有传感装置的攀爬机器人,将立体摄像机安装在一个六足机器人的胸部来获取图像信息,将获得的图像通过对光照模式的估计和去除,对图像进行改进,然后基于灰度统计的方法采用Otsu方法进行阈值处理,最后利用形态学运算提取裂缝信息;Jitesh J.Dhule等人[10]通过控制无人机的飞行、起飞和垂直降落来捕捉建筑物外墙的图像,然后基于边缘检测的方法采用Sobel算子识别建筑物垂直墙裂缝的边缘来获得裂缝的信息.

2 裂缝连接算法

本文提出一种基于NEAR模型的大型建筑物外墙裂缝连接算法,该算法首先对获取的墙面图像进行裂缝提取;然后用基于NEAR模型来表达提取后裂缝之间的连续性,最后采用二次贝塞尔插值完成裂缝连接,流程图如图1所示.

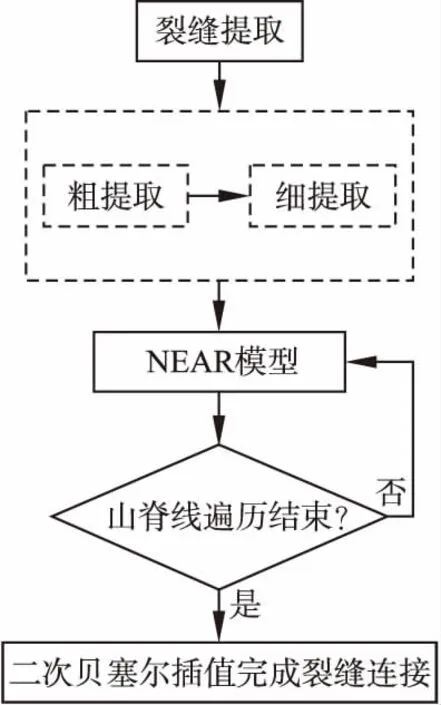
图1 裂缝连接流程图Fig.1 Crack connect diagram

2.1 裂缝提取

裂缝的提取包括粗提取和细提取两部分.首先将获取到的大型建筑物外墙面图像经过灰度转换、灰度线性变换增强[11]、双边滤波去噪[12]等预处理,然后结合OpenCV来实现裂缝的粗提取,分割出前景和背景部分.在双边滤波去噪时,有时会存留下一些较大的噪声,所以本文设置了一个阈值 H 来对裂缝粗提取后的所有连通域进行筛选,将面积小于阈值的连通域剔除掉,得到粗提取的墙面裂缝二值化图像,H根据具体情况而定,由实验得到的经验值,H取为10～15较合适.

采用连通域几何参数筛选法实现裂缝的细提取.裂缝一般被认为是一个具有一定长度走向的细长目标,具有连续、长宽比例悬殊、走向呈放射状等特点,根据这些限制条件将裂缝标识出来的方法我们称为连通域几何参数筛选法[13].裂缝具体识别指标有如下四个:

1)连通域的面积:指二值化后连通域中的像素个数;

2)连通域的最小外接矩形长宽比:表示该连通域的伸展情况,目标最小外接矩形的长与宽的比值;

3)连通域的矩形度:表示连通域的外观接近矩形的程度,目标面积和最小外接矩形面积之间的比值;

4)连通域的圆形度:表示连通域的外观接近圆形的程度,目标面积和最小外接圆面积之间的比值.

2.2 NEAR模型

获取的裂缝图像中,连续裂缝由于过窄或被灰尘填充或在预处理过程中产生断裂,就有可能造成最后检测的裂缝目标不连续、不完整,严重影响对于裂缝参数的评定.为了能够更加准确的获得裂缝的完整性,更加准确的评价墙面破损程度,本文提出了一种基于NEAR模型的裂缝连接算法对断裂的裂缝进行连接.

本文的NEAR模型是根据裂缝经过细化后的走向特征类似于山脊线而提出的.首先定义裂缝:S=(L,δ(L)),其中,L是裂缝的山脊线特征,δ(L)是裂缝的宽度信息.

NEAR模型的定义及根据NEAR模型判断相邻裂缝是否属于同一裂缝,算法如下:

1)对细提取后的连通域进行山脊线提取[14],得到山脊线集合L={L1,L2,…,Ln},并根据ε=f(δ(L))得到相应邻域半径εi,i=1,2,…,n.其中,f(·)根据具体情况选取,可为线性函数、平方根函数等等.由此可得山脊线的邻域表示,如公式(1).

U={Uε1(L1),Uε2,(L2),…,Uεn(Ln)}

(1)

2)邻域调整,整合裂缝,即将属于同一条裂缝的山脊线归为一类.山脊线邻域评价模型见公式(2):

(2)

算法过程图如图2(a)-图2(h)所示.

图2 NEAR模型算法过程Fig.2 Rideline neighborhood evaluation model algorithm process

2.3 裂缝连接

经过NEAR模型判断之后,可以得到属于同一裂缝的山脊线和对应的邻域,接下来将属于同一裂缝的所有山脊线进行连接,其中裂缝连接方法目前大多数是直线连接,而本文采用的是形如裂缝走势的曲线连接,曲线连接的拟合度会比直线连接的拟合度高,更符合裂缝的骨架结构.实现本文曲线绘制的方法采用的是二次贝塞尔插值方法.即山脊线与山脊线的连接采用二次贝塞尔插值方法,二次方贝塞尔曲线公式见公式(3),绘制原理过程图如图3(a)-图3(d)所示:

B(t)=(1-t)2Pi+2t(1-t)Pk+t2Pj,t∈[0,1]

(3)

其中B(t)表示要绘制的曲线,Pi表示起始点坐标,Pk表示控制点坐标,Pj为终点坐标.

图3 二次贝塞尔曲线绘制原理过程Fig.3 Quadratic Bezier curve drawing principle process

山脊线与山脊线的连接具体步骤如下:

1)以确定的山脊线的各区间的像素点作圆,圆心为山脊线上的像素点坐标,直径为该像素点对应的山脊线区间的裂缝宽度.

2)找出Li、Lj两条相邻山脊线的邻域半径圆交集的最短距离的像素点pi、pj和该像素点对应的相邻m(m一般取为2,3,5)个像素距离的像素点pi±m、pj±m,见图3(a)、图3(b).

3)经过点pi、pi±m和点pj、pj±m各自作一条直线,两条直线的交点为pk,见图3(b).

4)将pi、pj、pk三点代入二次贝塞尔曲线公式,绘制山脊线的连接线,如图3(c)、图3(d),得到连接线pi～pj.

5)取pi所在区间的邻域半径与pj所在区间的邻域半径的均值作为连接线的邻域半径.

当裂缝二值化之后断开较大,连接会无效.因为当裂缝二值化之后断开较大,如超过选取的邻域半径函数所得到的邻域半径时,则认定此时断开的距离已经足够远,可认为两条相邻的裂缝是独立的个体.

3 山脊线邻域半径的确定

在建立NEAR模型以及完成裂缝连接的过程中都用到邻域半径,本文中确定邻域半径的方法如下:

首先,通过间隔取点的方式对山脊线进行一定的平滑,以消除曲线的局部形状对整体山脊线走势判定的影响.在本文的实验中,取间隔点数N一般取为5至8之间,距离太小影响效率,距离太大误差增大.

若山脊线上的上一个按方向分割的曲线段的终点为Vi,则其同时为新一段的起点.按如公式(4)计算:

(4)

对曲线分割的区间及方向示意图如图4所示

图4 按右上角标识的四个方向对曲线进行分割Fig.4 Split the curve in the four directions identified in the upper right corner

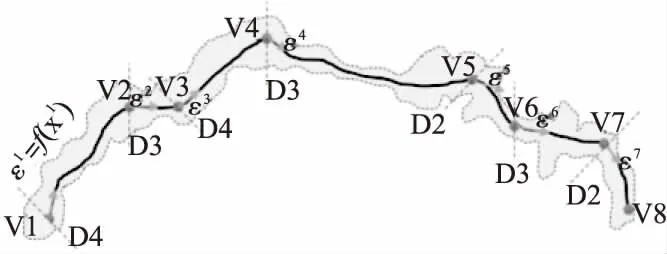
图5 按垂直于标识方向的方向扫描裂缝Fig.5 Scan the crack in a direction perpendicular to the direction of the mark

按垂直于标识方向的方向扫描裂缝,根据一定的映射关系f(·)求得裂缝在每一段上的邻域半径εi.其中,εi为第i段上沿山脊线上的像素点扫描截得的裂缝宽度集合.

4 实验结果及分析

本文采用如图6所示的无人机信息采集系统来获取大型建筑物外墙面图像,利用无人机搭载高倍可变焦相机围绕大型建筑物外墙拍照进行图像采集,通过无人机上搭载的测距传感器来确定无人机离墙面的距离d,保证拍照时成像尺度大致相同.每到一个航点时,当测距传感器测出无人机离墙面的距离为d时,相机自动拍照采集图像.

图6 无人机信息采集系统示意图Fig.6 Diagram of UAV information collection system

本文裂缝连接算法程序基于Visual Studio 2013开发,运行环境为Windows 10,运行内存为8GB.将300张外墙面图像用于本文算法的测试,并与K-D树连接算法进行实验对比.图7中列出了斜裂缝、纵裂缝、横裂缝6组实验结果图.

为了有效评估裂缝连接的效果,本文采用基于缓冲的Hausdorff距离的分值测量方法[15].Hausdorff距离是描述2组点集之间相似程度的一种量度,它是2个点集之间距离的一种定义形式:假设有2组集合A={a1,a2,…,ai},B={b1,b2,…,bi},则这2个点集合之间的Hausdorff距离定义为:

H(A,B)=max(h(A,B),h(B,A))

(5)

其中:

(6)

(7)

其中ma,mb分别为A,B,集合中点的个数.双向Hausdorff距离H(A,B)是单向距离h(A,B)和h(B,A)两者中的较大者,它度量了2个点集间的最大不匹配程度.将经过裂缝连接后的墙面裂缝看做一个点集,两裂缝之间的Hausdorff距离是通过裂缝像素点在图像中的坐标进行计算.

在本文中H(A,B)为人工裂缝分割图像和其他算法裂缝分割图像之间的距离,本文将人工分割的裂缝当作裂缝连接效果得分的基准图像,即将人工分割的裂缝作为一个标准,把通过K-D树连接算法和本文算法连接好的图像区域分别与手工分割的裂缝图像进行Hausdorff距离计算.人工分割的裂缝与真实裂缝图像存在微小的偏差,可忽略不计.A和B分别对应人工裂缝分割图像和其他算法裂缝分割图像中裂缝位置的集合,Score表示匹配的相似程度,总分值为100.Score越大表示两幅图像越相似,其分值计算如下:

Score=(1-H(A,B)))×100

(8)

在所有采集的外墙面图像中随机选出含有裂缝的300张图像用作算法测试实验的数据样本,其中斜裂缝图像100张,纵裂缝图像100张,横裂缝图像100张.将300张含有裂缝的外墙面图像用于本文算法和K-D树连接算法的实验对比.

本文中把人工分割的裂缝图像作为基准图像,将通过K-D树连接算法和本文算法连接好的图像区域分别与人工分割的裂缝图像进行Hausdorff距离计算,得到100组斜裂缝分值、100组纵裂缝分值、100组横裂缝分值,然后分别求出三组得分数据的平均值.表1和图8给出了本文算法和K-D树连接算法的性能平均得分比较, 经分析, 由于K-D树算法采用了最近邻原则进行裂缝连接,所以有时候会造成裂缝的误连接,将两个独立的裂缝连接在了一起,如图7(e)中的4、5图,而本文采用了NEAR模型对这种情况进行了限制,再加上本文算法在裂缝断裂处的连接环节采用的是二次贝塞尔插值,该方法更符合裂缝的走势,对于裂缝的连接拟合度会更大,而K-D树连接算法采用的是直线连接方法,与裂缝的骨架拟合度小.结果表明,本文的裂缝连接效果优于K-D树连接算法.

图7 6组实验结果图Fig.7 Six sets of experimental results

表1 两种算法连接效果得分对比
Table 1 Comparison of the scores of the two algorithms

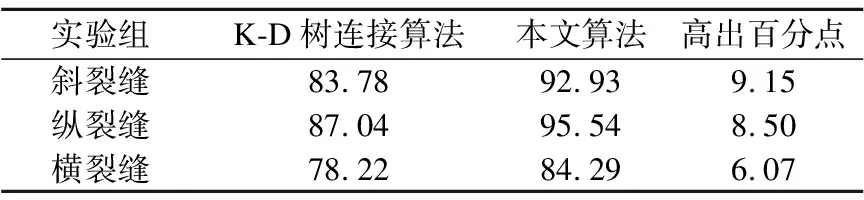
实验组K-D树连接算法本文算法高出百分点斜裂缝83.7892.939.15纵裂缝87.0495.548.50横裂缝78.2284.296.07

图8 连接效果得分对比Fig.8 Comparison of connection effect scores

5 总 结

本文针对大型建筑物外墙面图像检测时出现的目标不连续问题,提出一种基于NEAR模型的大型建筑物外墙裂缝连接算法.根据裂缝的走势特征类似于山脊线,首先提取裂缝的山脊线及其宽度信息来定义裂缝和山脊线邻域评价模型.利用NEAR模型来判断相邻的裂缝是否属于同一裂缝,将属于同一裂缝的两条山脊线重新连接整合形成一条山脊线,采用二次贝塞尔插值完成裂缝连接.对于山脊线邻域半径以及裂缝连接处宽度的确定是通过间隔取点的方式对山脊线进行一定的平滑,以消除曲线的局部形状对整体山脊线走势判定的影响,实验结果表明,通过本文实现的连接方法,可以使连接区域更接近实际裂缝.