铁路危险品运输系统单因素耦合风险折叠突变及控制机理研究*
黄文成,帅 斌,徐逸飞
(西南交通大学 交通运输与物流学院,四川 成都 611756)
0 引言
铁路危险品运输生产对安全要求极高,对铁路危险品运输系统风险进行分析具有重要意义。国内外学者在风险分析方面的研究主要采用静态的事件数、事故树、管理监督和风险树、软件-硬件-环境-生命件模型以及事故原因贡献因素模型[1-7]。上述模型均以分析事故原因为基础,属于系统安全静态分析方法;动态分析方法目前一般有马尔可夫链、有限状态机、Petri网、动态贝叶斯网络等[4-7],或从运输风险的影响因素出发,分析风险要素来源及其之间的互动组合关系(或耦合关系)来建立相应的分析模型[1-3]。
铁路危险品运输系统可看作是由人(如铁路相关运输人员)、机(如铁路运输机车车辆)、物(如所装载的危险品)、环(如运输铁路网络、周边环境等)、管(如铁路危险品运输管理系统)等5个子系统构成的具有不确定性特点的复杂系统[1-2]。各子系统存在引发安全事故的风险因素,系统安全取决于运输相关人员、机车车辆、铁路路网、周边环境、管理等各要素与环节之间的耦合协调工作,子系统中任何微小的风险能量变化都可能打破子系统原有的有序性、平衡性并造成该子系统崩溃,风险能量进一步传递、扩散后可能导致整个铁路危险品运输系统的局部或整体崩溃,从而引发火灾、爆炸、泄露等事故[1-4]。近年来,基于类比电场和磁场性质的方法,众多学者也尝试过采用风险场来分析铁路危险品运输系统耦合风险。如Wang等基于尖点突变模型[8-9],从数学层面上首次证明了铁路运输系统在受到风险因素干扰后,将形成一种类似于电场的效应,称为风险场(risk field);王喆和蔡梦贤[10]建立了铁路危险货物运输环境风险场强模型,并以此研究风险的变化情况,作者认为风险场的影响范围即为可能产生事故的风险波及范围,控制财产和人员处于风险场范围外即可较大程度上控制风险带来的影响。分析上述内容可知:铁路危险品运输系统安全状态的变化属于连续、动态过程,事故则可以理解为这一连续动态变化过程中突然出现的突变,即系统耦合风险突变为事故的过程。
为了保证铁路危险品运输系统的安全运行,有必要对耦合风险突变为事故的过程进行分析,并基于分析结果研究风险的控制机理。黄文成等[1]在利用N-K模型研究铁路危险品运输系统行车耦合风险的形成机理时,认为存在3类风险耦合形式:单因素、双因素和多因素风险耦合。篇幅限制,本文拟采用折叠突变[6-8]对单因素耦合风险进行分析;基于分析结果,建立单因素耦合风险形成突变的杜芬震荡模型,探索铁路危险品运输系统单因素耦合风险的控制机理,旨在为我国铁路危险品运输的安全事故预防控制和安全生产提供一定理论支撑。
1 铁路危险品运输系统单因素耦合风险折叠突变建模
突变理论由法国数学家雷内·托姆在1972年创立[8],用以刻画系统从一种稳定状态跃迁到另一种稳定状态的非连续变化现象。铁路危险品运输系统由安全状态突变为事故的过程具有多种状态,系统状态变化具有突跳性,因此采用突变理论建模是合适的[7]。铁路危险品运输系统在任意时刻的风险状态都可由给定n(n取值有限)个变量(x1,x2,…,xi,…,xn)确定[8],称xi为系统内部风险状态变量;同时铁路危险品运输系统受m(m一般不大于5)个独立变量(u1,u2,…,uj,…,um)控制[8],称uj为系统外部控制变量,本文认为人、机、物、环、管5个子系统的风险因素为5类独立控制变量,独立控制变量uj的值决定xi的值。铁路危险品运输系统安全状态可写成一组非线性方程组:
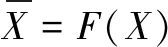
(1)
式中:X=(x1,x2,…,xi,…,xn)T是铁路危险品运输系统的内部风险状态变量;F=(f1,f2,…,fi,…,fn)是铁路危险品运输系统内部风险状态变量对于时间的变化率函数。对铁路危险品运输系统势函数进行奇异性分析,得到平衡曲面M和奇点集S[8]:
M:DxF(X)=0
(2)
S:detDxF(X)=0
(3)
非线性方程组可用泰勒级数展开式近似表达,消去泰勒展开式的幂级数次高项,可将非线性系统转化为突变势函数的势函数形式。对式(1)进行泰勒展开,并将其保留至二次项:
F(t)=a0+a1x+a2x2
(4)
令t=x-a1/2a2,则可得式(5),其势函数如式(6)所示,经过整理可得式(7):
F(x)=a2x2+a0-a12/4a2
(5)
(6)
V(x)=x3+(3a0/a2-3a12/4a22)x
(7)
令3a0/a2-3a12/4a22=u,则可以得到折叠突变关于状态变量x和控制变量u的标准势函数为V(x)。折叠突变的相空间是二维的,其平衡曲面M和奇点集S分别如下:
V(x)=x3+ux
(8)
3x2+u=0
(9)
6x=0
(10)
奇点集属于平衡曲面的一个子集,折叠突变的奇点集是一个点(0,0)。分岔集B是奇点集S在控制空间即直线x=0上的投影,也是一个点u=0。具体如图1所示。
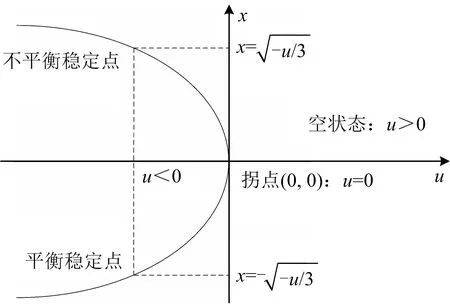
图1 折叠突变曲线、风险状态及平衡点Fig.1 Curve, risk state and equilibrium point of folding catastrophe
分岔集u=0把控制空间分成正u轴和负u轴:若u>0,则方程(9)无实数解,从而V(x)没有临界点,系统不能保持稳定;若u<0,则V(x)存在1个极大值点和1个极小值点,即1个不稳定平衡点和1个稳定平衡点;当u=0时,2个平衡点合并为1个拐点。铁路危险品运输系统的风险状态由稳定平衡点,经由拐点发生突变后,进入不稳定平衡点,系统将进入风险状态。为了进一步讨论5种单因素耦合风险折叠突变对系统状态产生的变化,可用第i种单因素(人、机、物、环、管)在第j年发生的铁路危险品运输事故概率刻画控制变量uij,则第i种单因素耦合风险在第j年的系统折叠突变平衡曲面Mij为:
(11)
式中:aij为小于0的常数;nij为第i种单因素耦合风险在第j年造成的事故数(单位:件)。基于上式还可得到第i种单因素耦合风险的系统折叠突变平衡曲面Mi:
(12)
2 单因素耦合风险杜芬震荡建模及风险控制机理
分析上述折叠突变平衡曲面可知:突变流形投影在平面上的分岔集B可确定铁路危险品运输系统的风险状态发生突变的临界值[8],因此可采用分岔分析法,找出折叠突变的分岔点,只需将分岔集B加以控制,即可控制铁路危险品运输系统风险突变的发生。引入含有立方项的杜芬震荡系统[8],分析单因素耦合风险分叉导致的折叠突变过程,研究风险突变的控制机理。
(13)

k2φ2+(2φε-3aφ3/4)2=F2
(14)
(k-c)2φ2+(2φε-3aφ3/4)2=F2
(15)
此外,还可研究基于系统外部影响振幅调节的线性反馈突变控制法:引入幅值反馈控制器σ=ρ·f·coswt,其中ρ为小参数,f为外部影响因素幅值调节系数,将σ代入式(13),同样采用多尺度法[8],得到含幅值控制系数f的分叉响应方程(证明过程略):
k2φ2+(2φε-3aφ3/4)2=(F+f)2
(16)
当铁路危险品运输系统中分叉响应方程的参数k,a,F确定后,可通过控制系统内部风险防御阻尼系数c或外部影响幅值调节系数f,研究协调参数ε与振荡幅值φ的关系,从内部阻尼控制、外部影响控制2方面研究铁路危险品运输系统风险的控制机理。
3 数据及仿真结果分析
按照引发事故的原因收集1985—2016年中国发生的铁路危险品运输安全事故件数,并计算相应的事故发生概率(1985—2008年数据来自文献[1]~[2],2008年以后由网上搜集),具体见表1。算例中aij取值为-1;则1985—2016年每年我国铁路危险品运输系统单因素耦合风险折叠突变结果如图2所示,其中(a)~(e)分别表示人、机、物、环、管,具体见式(11),(f)是我国铁路危险品运输系统单因素耦合风险人、机、物、环、管折叠突变的总体情况,具体见式(12)。
分析表1及图2,可以得出如下结论:1)人的单因素耦合风险突变对于铁路危险品运输系统的影响最大,是最有可能因为单因素突变导致事故的,其次是管、机、物。相比之下,环的单因素耦合风险突变对于铁路危险品运输系统的影响最小;2)铁路危险品运输系统风险状态突变具有多模态性,满足折叠突变的系统势函数具有1个极小值和极大值,从而使铁路危险品运输系统出现2种不同的状态;仿真结果可以看出,系统存在1个不稳定的平衡位置如拐点(0,0),此平衡位置在数学上不可微,具体描述为铁路危险品运输系统在此点具有不可达性;单一外部风险控制变量穿越分岔集B时的微小变化将导致铁路危险品运输系统风险状态从一个局部极大值临界点跳跃到另一个局部极小值临界点,这一现象可描述成折叠突变具有突跳性;铁路危险品运输系统的风险状态还具备发散性,指的是单一外部风险控制变量数值的有限变化会导致系统内部风险状态变量平衡位置数值的有限变化;此外铁路危险品运输系统内部风险状态还具有滞后性,可描述为第1个风险状态局部极小值跃向第2个局部极小值时的单一外部风险控制参数位置与由第2个局部极小值跃向第1个局部极小值时的单一外部风险控制参数的位置是不同的。

表1 1985—2016年我国发生铁路危险品运输事故数及概率Table 1 Number and probability of railway dangerous goods transportation accidents in china from 1985 to 2016 件

图2 1985—2016年我国铁路危险品运输系统单因素耦合风险折叠突变结果Fig.2 Single-factor coupled risk fold catastrophe of dangerous goods transportation system in china from 1985 to 2016
以协调参数ε为横坐标,振荡幅值φ为纵坐标,对方程(14)进行仿真研究,结果如图3所示。其中(a)为铁路危险品运输系统单因素耦合风险受到人为外力幅值F变化后的风险震荡仿真结果(F分别取值0.111 29,0.081 29和0.051 29;a=0.04和k=-0.0583),(b)为铁路危险品运输系统自带的内部风险防御阻尼k变化后的单因素耦合风险震荡仿真结果(k分别为0.03,0.05,0.07;a=-0.058 3,F=0.111 29)。结果显示:1)当外力幅值F=0.111 29时,ε∈(-∞,-0.198)∪(-0.077,+∞)时,1个ε仅对应着1个振荡幅值φ,此时系统是稳定的;当ε∈[-0.198,-0.077]时,1个ε就对应着2个振荡幅值φ,振幅出现了跳跃现象,在这个区间内铁路危险品运输系统将发生单因素耦合风险的折叠突变,系统变得不稳定;2)随着F取值的不断减小,不稳定的区间在不断减小,当F<0.05129后,系统将不再产生折叠突变;3)当k=0.03时,ε∈(-∞,-0.355)∪(-0.077,+∞),1个ε仅对应着1个振荡幅值φ,此时系统是稳定的;当ε∈[-0.355,-0.077]时,1个ε就对应着2个振荡幅值φ,振幅出现了跳跃现象,在这个区间内铁路危险品运输系统将发生单因素耦合风险的折叠突变,系统变得不稳定;4)随着k值的增大,不稳定区间在逐渐变小,当k>0.07后,系统将不再产生折叠突变。
基于图3结果,研究含内部风险防御阻尼控制系数c(式15)和外部影响因素幅值调节系数f的分叉响应方程(式16),仿真结果如图4所示。其中k=0.03,a=-0.058 3,F=0.111 29。图4(a)表示c=0和c=0.06时的铁路危险品运输系统单因素耦合风险的杜芬震荡情况;图4(b)表示f=0和f=-0.09,c=0.06时的铁路危险品运输系统单因素耦合风险的杜芬震荡情况。结果显示,随着内部风险防御阻尼不断增强(c数值变大),亦或系统或子系统受到的外部影响幅值得到控制(f数值变小),铁路危险品运输系统都将逐渐远离折叠突变,振幅不会再发生跳跃现象,系统将变得更加稳定、安全。即相关铁路危险品运输企业、部门等应该从2个方面采取措施,降低单因素耦合风险的折叠突变、保证运输安全:一是不断提高铁路危险品运输系统或子系统内部的防御体系,加强监督管理,加强系统抗风险能力;二是尽可能控制或消除外部风险影响因素,如人的不安全状态、物的不稳定状态、机的不良好状态、环的不可逆状态、管的不完善状态等,从根本上抑制铁路危险品运输状态发生变化,控制系统的单因素风险耦合折叠突变,从而保证运输安全。

图3 F和k取值不同时系统的杜芬震荡响应Fig.1 Duffing oscillation response of the system under different F and k

图4 c和f取值不同时系统的杜芬震荡响应Fig.4 Duffing oscillation response of the system under different c and f
4 结论
1)铁路危险品运输系统可受到人、机、物、环、管单因素耦合风险的影响。当耦合风险超过系统的安全阈值后,系统将突跳产生不可逆的安全事故。为分析这种突跳情况,建立了铁路危险品运输系统单因素耦合风险的折叠突变模型,采用1985—2016年中国发生的铁路危险品运输安全事故统计数据分析折叠突变,其中人的单因素耦合风险突变对于铁路危险品运输系统的影响最大,是最有可能因为单因素突变导致事故的,其次是管、机、物、环单因素耦合风险突变。
2)基于仿真结果分析了折叠突变的多模态性、不可达性、突跳性、发散性和滞后性。基于折叠突变模型,分别建立了含系统内部风险防御阻尼控制系数和外部影响因素幅值调节系数的杜芬分叉响应方程,研究铁路危险品运输系统单因素耦合风险的控制机理并对其进行仿真。结果显示:随着系统内部风险防御阻尼不断增强,或是外部影响幅值得到控制,铁路危险品运输系统都将逐渐远离折叠突变,振幅不会再发生跳跃现象,系统将变得更加稳定、安全。
3)相关铁路危险品运输企业、部门等应该不断提高铁路危险品运输系统或子系统内部的防御体系,加强监督管理,加强系统抗风险能力;同时尽可能控制或消除外部风险影响因素,从根本上抑制铁路危险品运输状态发生变化,控制系统的单因素风险耦合折叠突变,保证运输安全。另外还需要进一步基于突变原理,建立铁路危险品运输双因素耦合风险的尖点突变模型、三因素耦合风险的燕尾突变模型、四因素耦合风险的蝴蝶突变模型、五因素耦合风险印第安人茅屋突变模型,完善铁路危险品运输耦合风险突变成事故的机理,同时还需基于杜芬震荡模型分析各类模型的控制机理。

