基于有限元的局部突变位移载荷下埋地管道力学分析*

吴 锴, 张 宏

(1. 中国石油大学(北京) 安全与海洋工程学院，北京 102249;2. 中国石油大学(北京) 机械与储运工程学院，北京 102249)

0 引言

近年来我国地质灾害频发，地质灾害引起的地表位移对埋地管道结构的安全性构成重大威胁。埋地管道在敷设时不可避免的需要穿越多种类型的地区。其中以黄土湿陷、冻土融沉、盐渍土溶陷等为典型代表的局部突变型地质灾害是管道在穿越设计时面临的难题。随着我国油气资源需求量的不断增加，越来越多的油气管线投入生产建设，如何有效地保障穿越地质灾害段埋地管道结构的安全性受到广泛关注[1-5]。

地质灾害作用下埋地管道的安全设计一直以来都是工程关注的热点，Newmark等[6]最先提出断层位移作用下管道应力应变的计算方法，该方法基于三折线模型，假设管道只有拉伸刚度而无弯曲刚度，管道变形为直线同时管道的变形也只能由轴向变形吸收。他们认为侧向或垂向的运动均会导致管子产生一定的轴向应变。该方法已被多个国家的标准与规范采用。此后，Kennedy，Wang，Karamitros等[7-13]在解析方法上进行了不断的改进，得到了一系列断层位移作用下管道力学响应解析方法。Toshio等[14]进行了液化区埋地管线响应的相关试验研究，并建立数值分析模型，认为液化土壤中埋地管道轴向伸长率约为土体轴向应变的一半；王晓霖等[15]利用有限元模型分析了采空区管道变形规律及各点应力应变分布状态，并定量分析了埋深和敷设路线对管道轴向应力的影响；夏梦莹等[16-17]基于有限元模型分析了采空区管道应变规律，并对管道内压、埋深、管土摩擦系数等因素对管道应变的影响进行了定量分析；林均岐等[18-19]针对液化区土壤上浮问题，采用有限单元法分析了液化区长度、初始轴向力以及管材等参数对管道变形的影响。

虽然众多学者开展了多种类型地质灾害条件下管道应力应变响应，但尚未有针对局部突变型位移载荷的情况。因此，基于非线性通用有限元软件ABAQUS建立了埋地管道受局部突变位移载荷作用的有限元模型，考虑突变区域土壤性质与非突变区域土壤性质存在差异的情况，并在此基础上从管道轴心应变、弯曲应变的角度分析突变区域长度及突变位移量对管道受力的影响，研究结果可为工程中管道穿越地质灾害设计提供参考。

1 数值模型

1.1 管材模型与管土相互作用模型

选取西气东输二线使用的X80HD2管材作为研究对象[12]，管径1 219 mm，壁厚22 mm。管材最小屈服强度为530 MPa，最小抗拉强度为625 MPa，管材真实应力应变曲线如图1所示。采用ALA《Guideline for the Design of Buried Steel Pipeline》提出的非线性土弹簧描述管土之间的作用[20]。

图1 X80管材真实应力应变曲线Fig.1 True stress-strain curve for X80 pipe steel

1.2 有限元模型

对于局部突变型地质灾害来说，根据其载荷形式和结构形状的对称性，且为减小计算成本，提高计算效率，通过ABAQUS建立对称模型，对管道端部采用对称边界，采用土弹簧的形式来描述管土相互作用，模型如图2所示，根据式(1)取模型总长为非锚固段长度1 500 m，其中AB段采用壳单元来模拟，环向设置24个节点，轴向每0.4 m 1个单元，CB段是发生突变型位移管段，对该部分土壤节点施加位移载荷；其中DA段长度为1 000 m，每1 m 1个单元，从而消除远端边界的影响，DA段采用管单元来模拟，管单元较壳单元来说积分点较少，计算效率高，在处理本问题时由于远端管道变形较小所以采用管单元能大大缩小计算时间，提高计算效率，模型共包含62 049个节点，62 025个单元。

(1)

式中：La为管道一侧非锚固段长度，m；σs为管材屈服应力，Pa；A为管道截面面积，m2；Tu为轴向土弹簧极限抗力，N/m。

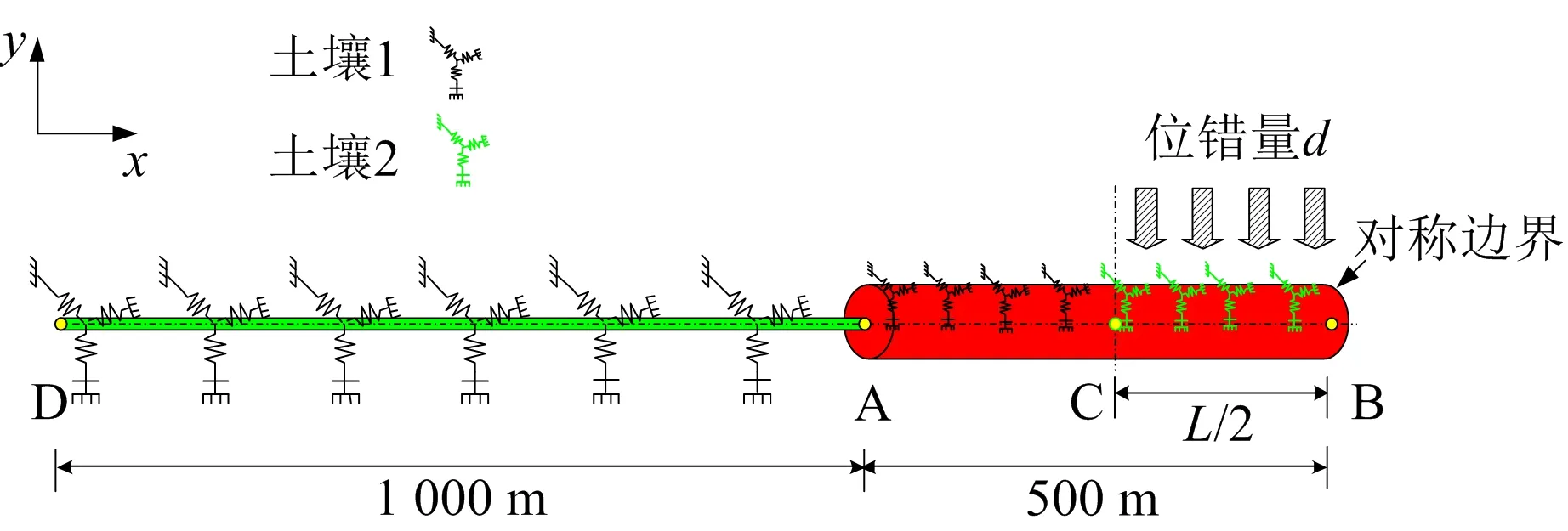
图2 有限元模型示意Fig. 2 Sketch of the finite element model

2 力学响应分析

2.1 局部突变位移载荷特征

黄土湿陷、冻土融沉等地质灾害发生位移部分的土壤通常与非突变区域土壤在性质上存在一定的差异。因此通过简化描述管土相互作用的土弹簧在突变区域与非突变区域是不同的。且这些地质灾害与倾角为90°的正断层在空间位移形式上存在一定的相似性，均是由土壤在垂直面内产生一定的位移，但与断层不同，这些地质灾害存在突变区域长度，如图3所示。突变区域长度与突变位移量作为局部突变型地质灾害中重要的工况参数，是影响管道受力状态重要的量。

图3 断层及其他突变载荷位移示意[3]Fig.3 Sketch of fault and other mutuation load displacement

2.2 突变区长度对管道受力状态影响

突变段长度L是影响管道受力状态的重要因素，其大小将决定管道在突变段的轴心应变、弯曲应变是否会发生耦合，从而在根本上导致结果的差异，本节从管道轴心应变、弯曲应变的角度出发，分析突变区长度L对管段受力状态的影响。

由于整个土壤与管道的位移发生在垂直面内，因此侧向土弹簧对管道变形影响不大，表1～2列出了各计算工况参数的取值。

表1 工况参数取值Table 1 Values of the case parameter

表2 土弹簧参数Table 2 Parameters of soil properties

图4给出了不同突变区位移δ下管道最大拉应变εtmax随突变区长度L的变化关系，可以发现，εtmax均随着L的增加先增加再保持不变，可以看出，在L大于80 m之后，所有计算工况下管道内最大拉应变值均不再发生明显变化，为进一步分析其原因，提取δ为3 m时，不同L下管道轴心应变及弯曲应变的分布，结果如图5、6所示。

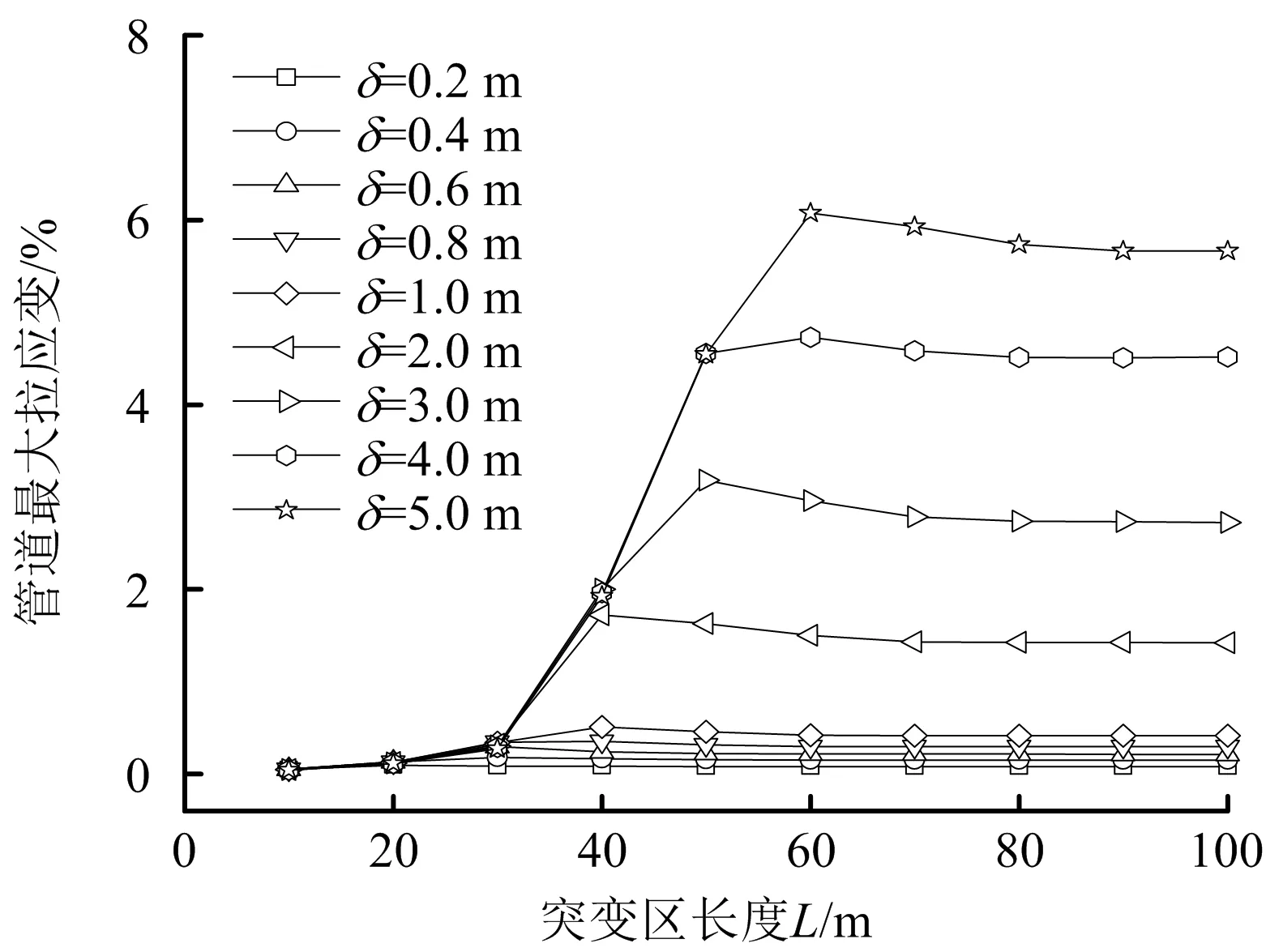
图4 管道最大拉应变随突变区长度变化Fig.4 The relationship between the maximum tensile strain of the pipeline and the length of mutated area

图5 不同突变区长度L下管道弯曲应变分布Fig.5 The distribution of the bending strain of the pipeline under different mutational length L

图6 不同突变区长度L下管道轴心应变分布Fig.6 The distribution of the axial strain of the pipeline under different mutational length L

综合图5，6可以发现，管道在受到该类型载荷形式的地质灾害作用下，主要产生弯曲变形，管道内弯曲应变较大，轴心应变相对于弯曲应变值较小，管道内最大应变主要以弯曲应变为主。对于轴心应变来说，L小于30 m时，管道内轴心应变几乎为0，而弯曲应变也较小，且可以发现，L从20 m增加到30 m时，管道弯曲应变有较为明显的增加。而当突变区长度增加至50 m时，管道内轴心应变及弯曲应变均明显增大，由于管道在突变区两侧均受弯，而此时对称边界处管道轴心应变及弯曲应变的值均较大，说明管道两侧变形导致的轴心应变、弯曲应变分别在突变区产生相互作用，继续增加L至70 m时，管道内轴心应变在对称边界处附近保持一定值不变，而对称边界区域附近依然存在着一定的弯曲应变，随着突变区长度超过80 m时，可以看出，对称边界区域弯曲应变已衰减为0，管道轴心应变依然保持不变，说明管道两端的变形在突变区域内不再产生叠加，所以管道最大拉应变也不再发生变化。图7给出了δ为3 m时，不同L对应的管道变形云图。

图7 不同突变区长度管道变形云图Fig.7 The deformation contours of pipeline under different mutational length

2.3 突变位移对管道受力状态影响

对于给定某一突变区长度L，当L小于Lcrit时，突变位移δ也是同样影响管道应力状态重要的因素，在本节采用数值模拟方法，从分析管道轴心应变、弯曲应变的角度出发，分析δ对管段受力状态的影响。

图8与图9给出了在不同L下管道内最大拉应变与压应变随δ的变化关系，可以看出，当L不同时，管道内最大拉应变随突变位移变化的规律各不相同，在L小于20 m时，随着δ的增加，管道内应变几乎保持不变，且该应变值均较小；当L大于20 m，随着δ的增加，管道内的应变均先增加并随后在位移达到某一值(δcrit)后保持不变，值得一提的是，不同L对应的δcrit各不相同。同时可以看出，在管道应变整体增加段，突变区长度对管道应变结果影响不大。

图8 管道最大拉应变随突变位移变化Fig.8 The relationship between the maximum tensile strain of pipe and displacement of the mutational area

图9 管道最大压应变随突变位移变化Fig.9 The relationship between the maximum compressive strain of pipe and length of the mutational area

图10 不同突变位移下管道轴心应变分布Fig.10 The distribution of axial strain of pipeline under different abrupt ground displacement

提取了突变区长度L为50 m时，不同突变位移δ下管道内轴心应变与弯曲应变的分布情况，结果如图10和图11所示，可以看出，随着突变位移的增加，管道内轴心应变与弯曲应变均随之增加，但当突变位移大于4 m时，管道内轴心应变与弯曲应变均不再发生变化。另外注意到管道的轴心应变与弯曲应变均在非突变区域段取最大值，且该位置离突变区域较近。提取该段土壤节点在垂向上的反力如图12所示，可以发现，在δ达到4 m时，此时50 m区域内垂向弹簧均进入塑性，对应的土壤节点反力均相同，即管道受到均布荷载作用，所以在位移超过4 m时，管段内轴心应变与弯曲应变不再变化。对应的管道变形云图如图13所示，从云图中同样可以看出，4 m和5 m突变位移下的管道变形几乎完全相同。

图11 不同突变位移下管道弯曲应变分布Fig.11 The distribution of bending strain of pipeline under different abrupt ground displacement

图12 不同突变位移下垂向土弹簧反力分布Fig.12 The distribution of reaction force of the veritcal soil spring under different abrupt ground displacement

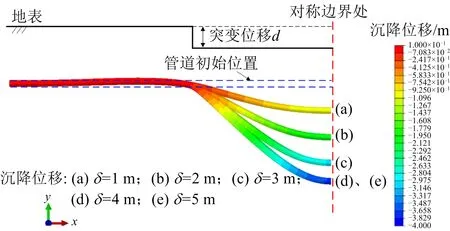
图13 不同突变位移下管道变形云图Fig.13 The deformation contours of pipeline under different abrupt ground displacement

3 结论

1)针对局部突变型地质灾害，管道内弯曲应变较轴心应变值较大，管道以受弯为主。同时突变型位移荷载作用下管道受力状态较为复杂，突变区长度L及突变位移值δ是影响管道应变重要的参数，在不同工况参数下根据L和δ的值，管道受力分为3种状态。

2)当突变区长度L大于临界突变区长度Lcrit时，管道弯曲应变在突变区域内不产生叠加，且突变区域内轴心应变值不再发生变化，此时该突变型位移荷载作用下的管道应变响应等同于2个垂直正断层，此为第一种受力状态。

3)当L小于Lcrit时，随着δ的增加，管道的应变不断增加，突变位移区域两端垂向土弹簧逐渐进入塑性阶段，并随着δ的增加不断向突变中心处扩展，有越来越多的垂向弹簧进入塑性，在应变增加段，L对管道设计应变的影响较小，即为第二种受力状态。

4)在第二种受力状态基础上，当继续增加δ至临界突变位移值δcrit时，在垂向上所有土弹簧均进入塑性，管道相当于受到均布荷载的作用，此时即使再增加δ，管道应力应变也不再发生变化，即为第三种受力状态。