磁致伸缩材料与石英音叉复合低阻尼谐振磁电效应*

李大威,卞雷祥*,卜雄洙,郭 涛,张 胜

(1.南京理工大学机械工程学院,南京 210094;2.陆军工程大学野战工程学院,南京 210094)

磁致伸缩/压电复合材料具有结构简单、制备难度小和磁电系数大等优点,在磁传感器、磁电换能器等领域具有广泛的应用前景[1-3]。在磁场作用下,磁致伸缩材料由于磁致伸缩效应发生磁致伸缩应力/应变,传递到压电材料后,由于压电效应产生电输出,当激励磁场频率接近磁致伸缩/压电复合材料或结构的谐振频率时,磁电效应能够得到显著增强。这种谐振状态下磁电效应得到显著增加的特性,在磁电传感器与换能器领域有着广泛的应用前景[4-9]。理论分析表明,谐振式磁电复合磁场传感器的磁电电压系数与复合材料的有效机械品质因数(Q值)成正比[4]。Dong等制备Terfenol-D/Pb(Zr,Ti)O3磁电复合材料,有效机械品质因数为49.9,谐振状态下的磁电电压系数比非谐振状态下的磁电电压系数大100倍[5]。为进一步提高品质因数,Xing等将具有高品质因数的弹性钢引入到Terfenol-D与PZT中间构成三相复合材料,谐振磁电电压系数为40 V/cm Oe,Q值增加到78,相比Terfenol-D/Pb(Zr,Ti)O3叠层复合方式,Q值并未得到显著增强[6]。Marauska等制备SiO2/Pt/AlN/FeCoSiB磁电复合材料的Q值为160,磁电电压系数为2 390 (V/m)/(A/m)[7]。Yarar等制备Si/SiO2/Pt/AlN/FeCoSiB谐振式磁电复合传感器的Q值为310,磁电电压系数为5 kV/cm Oe[8]。Jahns等制备AlN/Fe70.2Co7.8Si12B10/Si磁电复合材料的Q值为1 300,磁电电压系数为9 700 V/cm Oe[9]。进一步的,Kirchhof等又制备了两种类型的AlN/Fe70.2Co7.8Si12B10/Si复合悬臂梁结构,置于真空环境下Q值分别从1 400提高到5 800以及156提高到1 700[10]。

实际上,现有的磁致伸缩与压电材料叠层复合方式下,磁致伸缩层与压电层之间通过应变实现耦合,由于磁致伸缩材料本身具有高磁机阻尼,磁致伸缩/压电复合结构的有效Q值被限制。根据唯象理论,磁致伸缩效应是磁致伸缩材料在磁化过程中磁畴增大变形和旋转产生的,而磁畴运动势必带来能量耗散,因此很难找到一种同时具有高压磁系数、高Q值和磁弹性内耗对磁场没有依赖性的磁致伸缩材料[11-12]。幸运的是,有很多高Q值的压电材料如石英晶体、ZnO、AlN等[13-14]。U形石英音叉谐振器具有极高Q的值[15]。本文将U形音叉底端与磁致伸缩材料复合设计磁电复合结构,其中磁致伸缩材料的高磁机阻尼被隔离,其Q值主要取决于音叉谐振器自身,在谐振状态下磁电响应得到增强。

1 复合磁电敏感单元结构组成及原理

磁致伸缩材料与石英音叉复合的谐振磁电敏感单元由石英音叉、FeGa片与玻璃衬底三部分组成,如图1所示。

图1 FeGa与石英音叉复合结构

石英音叉由频率为32.768 kHz的商业晶振去掉封装后得到,石英音叉的两根叉指相互平行,由于两根叉指的振动方向相反,底部结合区域的应力应变和力矩相互抵消,实际形成应力/应变解耦区域。器件设计将解耦区域固定到磁致伸缩材料,对谐振器的Q值影响极小。石英音叉的具体尺寸参数参考图2和表1所示,其中Vd和G分别代表正电极和负电极。

图2 石英音叉结构尺寸

表1 石英音叉的尺寸参数

该器件的磁-机-电转换过程可看作一个受迫振动过程。在交变磁场作用下,磁致伸缩材料由于磁致伸缩效应而发生伸缩,磁致伸缩力传递到石英音叉迫使音叉振动,当交变磁场的频率与石英音叉的谐振频率一致时,石英音叉的振动幅度最大。由于磁致伸缩材料的压磁系数随偏置磁场的变化而发生变化,相应地,不同偏置磁场作用下,传递到石英音叉上的磁致伸缩力就有所不同,音叉的输出电流也会产生变化。

2 理论分析

交变磁场Hac=H0cos(ωdt)激励下,磁致伸缩材料产生的动态作用力Fac可表示为

Fac=F0cos(ωdt)

(1)

其中

F0=βAMdM(Hdc)H0

(2)

式中:dM(Hdc)是偏置磁场Hdc下磁致伸缩材料的压磁系数;H0是交变激励磁场的幅度;ωd为交变激励磁场的角频率;AM为磁致伸缩材料的横截面积;β(0<β<1)为力传递效率。

石英音叉的叉指可看作悬臂梁,简谐激励下,弯曲振动的挠度为w(y,t)=φ(y)φ(t),其中φ(y)为悬臂梁的横向位移沿长度方向的振型分布函数,本文中石英音叉工作在一阶振动模态,对应一阶振动模态的振型分布函数[16]

φ1(y)=cosh(γ1y)-cos(γ1y)-

(3)

式中:γ1L=1.875,L为悬臂梁长度。

φ(t)为悬臂梁在简谐激励下横向位移随时间t的变化函数

φ(t)=A0cos(ωdt+θ)

(4)

磁电敏感单元可看作受迫振动系统,在交变激励磁场作用下,音叉叉指的运动微分方程可表示为[17]

(5)

式中:m、ω1和Q分别是石英音叉叉指的等效质量、谐振频率和品质因数。将式(4)代入式(5)解得

(6)

(7)

假设沿叉指长度方向(Y轴)仅存在由叉指的弯曲产生的轴向应变S2,且其他方向的应力为零。则沿Y方向的应力T2

(8)

式中:E为杨氏模量,x(-H/2≤x≤H/2)为离中性轴的距离,电极厚度忽略不计。

假设沿x方向和沿z方向应力为零,石英的压电方程可表示为

(9a)

(9b)

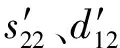
(cosφ1)2(sinφ1)2-2s14(cosφ1)3sinφ1

(10a)

(10b)

(10c)

式中:s11、s33、s55、s13和s14均为柔顺性系数;d11和d14为压电常数;ε11为介电常数;φ1为石英晶体沿X轴旋转的角度。本文采用的石英音叉为(xyt)2°切型,即φ1=2°。可解出

叉指上表面电极与下表面电极相通,具有相等的电势,则E1=0,代入式(9a)和式(9b)可以得到

(11)

对叉指上表面电极区域(-B/2≤z≤B/2,0≤y≤Le)以及下表面电极区域进行积分,得到总的电荷量[19-20]

(12)

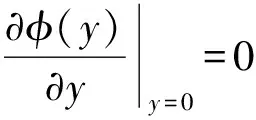
(13)

(14)

当交变激励频率ωd接近于谐振频率ω1(ωd≈ω1)时,石英音叉输出谐振磁电电流Ires

(15)

可以看到,石英音叉在谐振点处的谐振电流输出值与石英音叉本身Q值大小成正比。在谐振点处磁电敏感单元的磁电电流系数为

(16)

压磁系数dM(Hdc)是偏置磁场的函数,使得磁电电流系数αI也成为偏置磁场的函数。磁电电流系数对偏置磁场的灵敏度

(17)

3 器件制备与测试

石英音叉谐振器取自商用32.768 kHz晶振,去掉晶振封装外壳与底座之后,便得到器件制备所需的石英音叉谐振器。所用磁致伸缩材料为FeGa合金,尺寸为9.6 mm×1.4 mm×0.5 mm,沿长度方向磁化。磁电敏感单元的制备主要有3个过程:①采用环氧树脂胶将FeGa片的两端粘接到玻璃衬底上,两端的粘接区域约1.5 mm×1.4 mm;②采用环氧树脂胶将石英音叉底部粘接于FeGa片中部;③焊接石英音叉电极引线。

图3 实验测量系统

磁电效应测量系统如图3所示,主要由锁相放大器(Zurich,MFLI 5 MHz)、压控电流源(Stanford,CS580)、程控电流源(北京乐真电子科技有限公司,F2030)、亥姆霍兹线圈、螺线管线圈、I-V转换模块以及计算机组成。MFLI锁相放大器的内置信号源输出的交流电压信号给CS580压控电流源,输出所需幅度的交流电流激励螺线管线圈,产生交流激励磁场Hac。待测器件置于螺线管线圈中心,在交变磁场作用下产生电输出。磁电敏感单元可看作一个电流发生器,输出电流信号经过I-V转换模块转换成电压信号后输入到锁相放大器。亥姆霍兹线圈的磁场-电流转换系数为28 Oe/A,在程控电流源输出电流(0～10 A)过程中可输出0～280 Oe的偏置磁场Hdc。磁电敏感单元与I-V转换模块的连接方式如图4所示。

I-V转换模块的理论增益为106V/A,实验测量I-V转换模块在频率为33 kHz时的实际输出电压与输入电流曲线如图5所示。拟合后的线性方程为y=1.2x-0.014,其中y为输出电压,单位为mV,x为输入电流,单位为nA。I-V转换电路的实际增益约为1.2×106V/A。

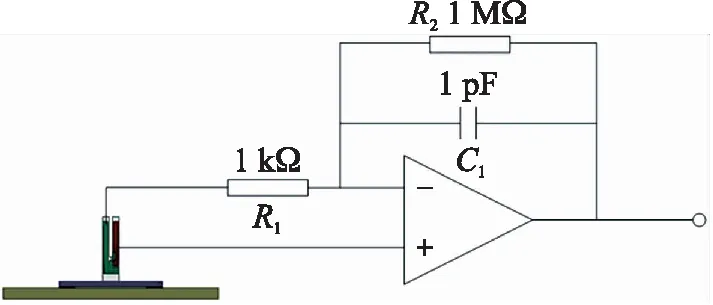
图4 磁电敏感单元与I-V转换模块连接方式

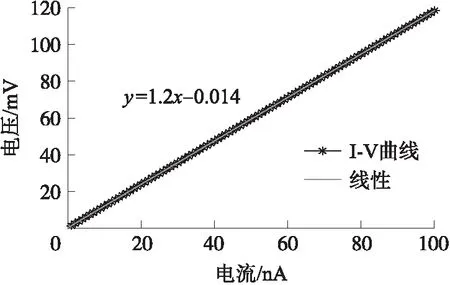
图5 I-V转换模块测量曲线

图6 不同偏置磁场作用下磁电电流输出随频率变化曲线

4 实验结果与讨论

设置MFLI锁相放大器的电压输出幅值为 100 mV,压控电流源的转换系数为50 mA/V,此时压控电流源输出幅值为5 mA的交流电流信号激励螺线管线圈,从而产生幅值为0.1 Oe的交变激励磁场。测得在不同偏置磁场下磁电敏感单元的磁电电流输出幅值及相位曲线如图6所示。可以看到,磁电电流曲线存在显著的谐振峰,即在音叉谐振频率下磁电电流输出达到最大值。在偏置磁场为2 80O e时,谐振状态相比于非谐振状态的磁电电流增量为93.8 nA。由式(15)可知,磁电电流输出峰值正比于磁电敏感单元的Q值。非谐振频率处也有较大的磁电电流输出(约17 nA),这可能是由于实验装置回路以及电极引线等存在寄生电容通过电磁感应产生的感应电流。

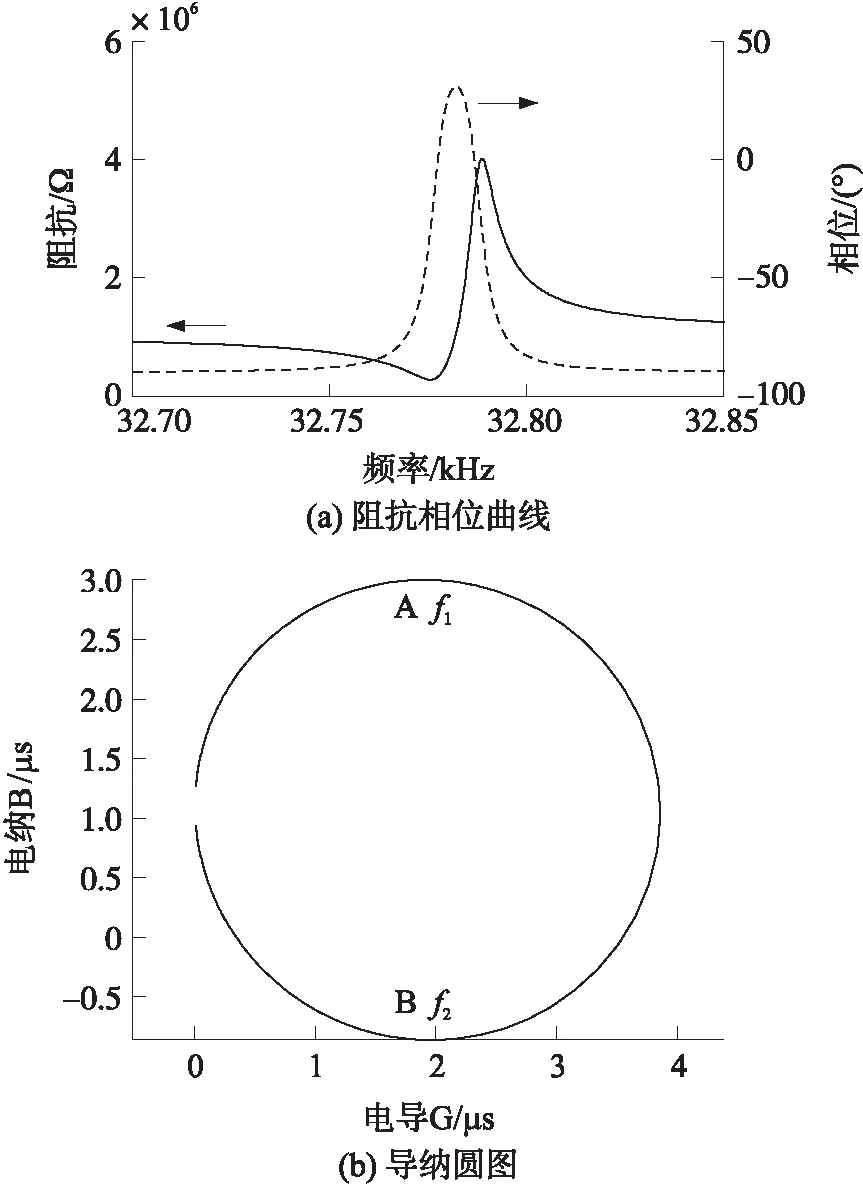
图7 Hdc=0 Oe时的阻抗相位曲线和导纳圆图

图8 不同偏置磁场下磁电敏感单元Q值曲线

可以看到,磁电敏感单元的Q值在5 034附近波动,Q值出现波动的原因可能是由于测量方法引起的误差。阻抗曲线和导纳圆测量采用线性扫频方式,扫频区间32.7 kHz～32.85 kHz,点数600点,即扫频间隔仅为0.25 Hz,而Q值5 034对应的3 dB带宽约为6 Hz,扫频间隔可能造成3 dB带宽计算产生的最大误差为±0.5 Hz,从而导致Q产生波动。

由图6和图8可以看到,磁电敏感单元的谐振频率和品质因数随偏置磁场的变化较小,这得益于石英音叉的解耦结构和磁电敏感单元的复合方式。在石英音叉解耦区域应力/应变方向相反,弯矩相互抵消,石英音叉的解耦区域固定在磁致伸缩材料上,磁电敏感单元在工作过程中的谐振频率与品质因数受到的影响极小。

图9为磁电敏感单元输出的磁电电流随交变激励磁场幅度变化曲线。测量时设置偏置磁场Hdc=140 Oe不变。

图9 磁电电流输出随交变激励磁场幅度变化曲线

由图9可见,磁电电流随交变激励磁场变化呈线性变化,这与式(16)是相符的。在频率为30 kHz、32 kHz、32.774 kHz、34 kHz、35 kHz时,磁电电流对交变激励磁场幅度的灵敏度分别为145.3 nA/Oe、166.2 nA/Oe、799.2 nA/Oe、196.4 nA/Oe、208.4 nA/Oe。当频率在谐振频率32.774 kHz附近时,磁电电流对磁场的灵敏度显著增强。

图10为不同固定频率交变磁场激励下,磁电敏感单元的磁电电流系数随偏置磁场变化曲线。偏置磁场从0 Oe增加到280 Oe,间隔为5 Oe。

图10 不同固定频率激励下磁电电流系数随偏置磁场变化曲线

由图10可见,磁电电流系数随偏置磁场变化明显,在偏置磁场为100 Oe～180 Oe范围内线性度较好,在此范围内比较了5个不同频率下磁电敏感单元对静态磁场的灵敏度,发现激励信号在谐振频率32.774 kHz时灵敏度最大,为5 (nA/Oe)/Oe。

5 总结

采用石英音叉谐振器与磁致伸缩材料复合设计了低阻尼谐振式磁电敏感单元,音叉谐振器特殊的结构特征使得磁致伸缩材料的磁机阻尼被隔离,从而复合结构可获得极高的Q值。制备FeGa/石英音叉复合磁电敏感单元样品测试表明:谐振磁电电流系数达到799.2 nA/Oe,空气中Q值达到5 034,谐振磁电电流系数对偏置磁场变化的灵敏度达到5 (nA/Oe)/Oe,可用于静态或准静态磁场测量。