薄壁球面构件普旋法兰起皱预测方法评价
杜陈阳, 孔庆帅, 赵亦希, 于忠奇
(上海交通大学 上海市复杂薄板结构数字化制造重点实验室, 上海 200240)
旋压成形是一种近净成形的加工技术,具有材料利用率高、产品精度高、产品性能好、所需成形力小、模具成本低、柔性化程度高等突出优点,在大型薄壁构件,尤其是航空航天薄壁构件的制造中具有重要地位[1-2].在大型薄壁曲面构件旋压成形方面,国外航天企业进行了大量的研究,并已经在火箭燃料贮箱箱底制造上得到成功应用.目前,我国正在攻克箱底构件的整体旋压成形技术,以进一步提高我国大型运载火箭的制造水平[3].
在箱底这类曲面薄壁零件旋压过程中,理论上半锥角由封头顶端的90° 变为外端的0°.由于剪旋过程中材料壁厚遵循半锥角的正弦规律,相应的材料厚度由初始厚度减为0,因此不可能采用一道次剪切旋压工艺完成成形.工程上采用剪切旋压和多道次普通旋压复合成形的工艺方式[4].而在普通旋压过程中,法兰周向承受压应力作用,而且一般情况下法兰边处于无约束的自由状态,容易产生起皱缺陷,导致构件旋压加工失败.法兰起皱是普旋成形过程中最常见的典型缺陷之一.为了更合理规划旋压道次和旋轮工艺轨迹,避免旋压过程起皱缺陷的发生,学者们对旋压过程起皱问题进行了大量的研究.

图1 旋压试验Fig.1 Spinning test
在起皱机制方面,Zhan 等[5]利用数值仿真方法研究了锥形件旋压法兰起皱过程中应力应变场的演变特征,并给出进给比与锥形件法兰起皱的内在关系.Xia 等[6]采用试验方法研究了圆筒形件普旋过程板厚和进给比等关键参数对法兰起皱的影响,并建立了相应的成形窗口.目前对于普旋过程旋压起皱产生机制已经有较深入认知,这些研究不仅为起皱判据的建立奠定了理论基础,而且为控制起皱缺陷提供了明确的工艺选择.合理的起皱判据对于旋压工艺数字化设计是十分必要的.Kleiner等[7]和Sebastiani等[8]研究了普旋成形的动态起皱过程,并将旋压力的突变作为旋压成形法兰起皱的判据.Wang等[9]基于Abaqus软件分析了低碳钢杯形件普通旋压中旋压力与起皱发生的关联,并指出:可以用旋压力振荡作为法兰起皱的判据.Liu等[10]基于LS-DYNA软件分析了无芯模多道次旋压成形过程,指出:法兰起皱会导致成形过程中应变能迅速增加,可以此来判定起皱发生时刻.Watson等[11]在研究杯形件普旋起皱时,将变形区弹性应变能的振荡作为法兰起皱发生的判据.Kong等[12]基于能量法和塑性屈曲理论建立了旋压法兰失稳数学模型,并结合数值仿真,提取准确应力应变场等信息,完成了大径厚比构件旋压起皱预测.此外,在薄板成形中,往往采用几何感官法来评价起皱是否产生以及波纹严重程度.目前,对于旋压法兰起皱发生的判定方法,可以总结为几何直观法、旋压力法、弹性应变能法和塑性屈曲法.在文献报道中,这些方法均具有一定的预测精度.
在大型薄壁曲面构件工艺设计时,采用传统的试错法进行工艺性评估,将带来试制周期和材料成本的增加,这时运用精确的数字化工艺评估是十分必要的.为此,选择合适的起皱评价方法在数字化工艺设计中是首要解决的问题.然而,对于薄壁曲面构件旋压法兰起皱预测而言,上述这些方法的评价可靠性缺少对比研究.本文以铝合金球面薄壁构件第一道次旋压为研究对象,通过数值仿真和试验方法,对比研究上述评价方法对法兰起皱预测的适用性,进而给出合理的建议,为大型曲面薄壁构件工艺规划提出合适质量评价手段.
1 球面构件第一道次普旋法兰起皱试验
曲面类零件第一道次旋压成形过程中,板坯由平面状态变为曲面状态,在整个多道次旋压成形过程中变形量最大,对构件后续成形成功与否起着至关重要的作用[13].为此,本文针对第一道次普旋过程,开展铝合金球面构件普旋法兰起皱试验.
铝合金球面构件普旋法兰起皱试验在Okay800数控旋压机上完成,如图1(a)所示.所用试验材料为直径200 mm、厚度1.8 mm的2024-O铝合金板,将其旋制成半径为70 mm的半球面构件,芯模、旋轮以及尾顶的具体尺寸如图1(b)所示.旋轮进给比选用1 mm/r,主轴转速为200 r/min,旋轮与芯模间隙保持为1.8 mm.
为了探究半球形构件第一道次普旋成形法兰起皱的极限成形角,旋轮从芯模的平台顶部开始进行贴模旋压成形.试验方案如图2(a)所示,从芯模顶部的30° 处开始,每5° 成形一次,直到旋压至55° 停止.图2(b)所示为板坯初始状态,图2(c)~(h)所示为法兰起皱过程.由图2可见:法兰在成形初始阶段基本保持平直;当成形至40° 时,法兰开始出现轻微翘曲变形;当成形至45° 时,法兰开始出现明显起皱波纹,之后随着成形角度的不断增大,法兰的起皱波纹逐渐加剧;当成形至55° 时,法兰起皱波纹与旋轮碰撞,产生干涉,机床振动明显,成形终止.
通过铝合金半球形件第一道次普旋成形法兰起皱试验,明显可以观察到法兰起皱现象的发展过程.以法兰能否保持平直状态为几何外观标准,判断法兰是否起皱.由图2可以确定:法兰起皱发生时刻在成形角为35° 至40° 之间,因此将其均值37.5° 作为法兰起皱发生时刻.

图2 法兰起皱试验结果Fig.2 Flange wrinkling test results
2 球面构件旋压数值建模
在上述起皱评价方法中,均需要从数值仿真中提取应力应变场和几何信息,因此建立上述试验过程的数值仿真模型.

板坯网格划分以三维八节点线性减缩积分六面体单元SC8R为主,同时,为了控制板料网格单元合理的纵横比,选用三维线性减缩积分楔形单元SC6R作为过渡单元进行网格划分;另外,为防止出现沙漏问题,选择增强的沙漏控制.仿真中,旋压运动方式与试验工况相符,旋轮运动轨迹通过控制参考点的坐标变换实现;根据旋压数值仿真文献[14-15],各接触对的摩擦系数分别假设为:板料与芯模0.2,板料与尾顶0.5, 板料与旋轮0.02.

图3 球面件旋压数值仿真模型Fig.3 Finite element model of spinning process

E/GPaυσs/MPaK/MPan71.30.3370.06308.62 0.234

图5 法兰边缘轴向波动Fig.5 Axial fluctuation of the flange edge
为了正确评价各种起皱评价方法的合理性,可靠的数值计算是必要的.将数值仿真结果与对应试验值进行对比,验证旋压仿真模型的可靠性.首先,采用Faro三维激光扫描测量臂对旋压件内外表面轮廓进行扫描,获得其内外表面的三维坐标点云.然后将点云导入逆向工程软件Geomagic Qualify中进行数据处理,最终得到试验件壁厚分布结果.将试验结果与仿真结果进行对照,如图4所示.试验件周向壁厚分布比较均匀,选择轴向已成形区的壁厚分布与仿真结果进行比较验证.结果表明,数值仿真厚度与试验测量壁厚最大偏差为 4.2%,这说明该数值仿真有较好的准确性.
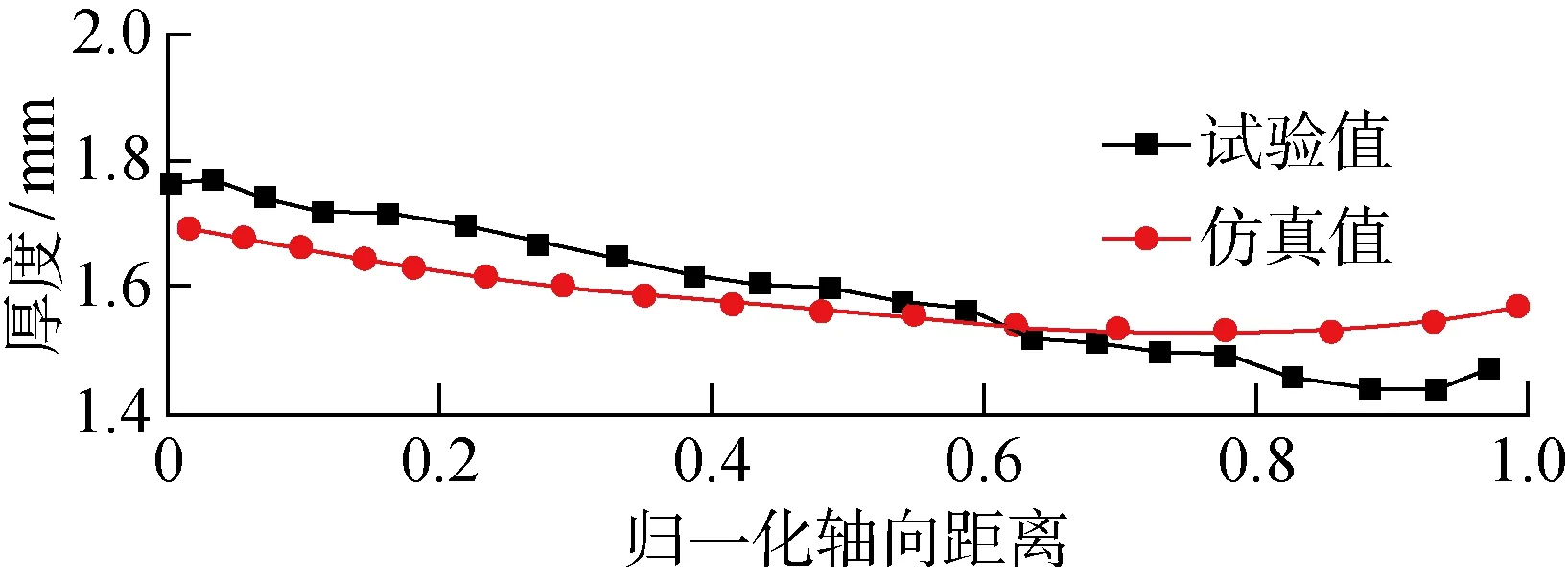
图4 仿真计算结果与试验结果的比较Fig.4 Comparison of the finite element results and the test results
3 预测方法对比分析
由现有文献可知,目前用于定量判断旋压法兰起皱的方法主要有4类:法兰几何波动、旋压力、弹性变形能和基于塑性失稳理论的预测模型.本节从半球形零件第一道次普旋仿真中提取所需的各类仿真数据,包括应力应变场和几何信息,计算各起皱方法的预测值,并和试验对比评价各起皱方法的适用性.
3.1 法兰几何波动法
法兰几何波动法是通过从旋压仿真中提取的旋压法兰边缘轴向波动的标准差来表征法兰的波动情况.图5(a)所示为法兰边缘轴向波动的标准差(e1)随成形角α的变化曲线.可以发现:在成形初期,即 25°~35° 范围内,由于旋轮对法兰存在弯曲效应,法兰边缘波动程度在小范围内振荡;当成形角度到达35° 附近时,法兰轴向波动程度开始加剧,表明法兰起皱波纹产生,这与法兰起皱试验结果很接近.因此,可以采用法兰边缘轴向波动的标准差来识别法兰起皱发生时刻.
为量化起皱发生时刻,对标准差曲线进行平滑处理,并进行一阶求导,如图5(b)所示,将标准差开始增加的时刻作为起皱发生时刻,确定其为32.8°.与前面试验结果相比,该方法超前预测了4.7°,误差达到12.5%.误差的原因可以归结为:试验起皱是通过感官来评价的,具有滞后性.从图5(a)上亦可以经验性判断起皱快速演变的时刻,因此几何直观法在科学与工程上都较为适用于起皱发生时刻的预测.
3.2 旋压力法
为了判断旋压力与法兰起皱发生时刻的关联,从数值仿真中提取了旋轮载荷的合力(F),如图6所示.可以看出:旋压力变化情况可以大致分为3个阶段,从旋压开始至成形角32° 附近,为旋压初始阶段,该阶段旋压力振荡相对不强,振荡现象主要是由于旋轮与板料的接触摩擦等导致;之后旋压力随成形过程不断增大,振荡逐渐加强,后期幅值也开始变大,该阶段处于起皱阶段,但无法获得普适性的量化分界点;最后,在成形角52° 附近时,旋压力曲线开始明显下滑,表明法兰波纹已经很明显,并与旋轮接触,法兰稳定性难以维持.

图6 旋轮旋压力变化Fig.6 Change of spinning force
旋压力变化的3个阶段界限不是很清晰,只能定性地判断起皱是否发生,难以用数学工具描述起皱时刻.相对而言,通过多项式拟合方法可以量化获取旋压力极值的时刻.
本研究发现:旋压力曲线峰值所对应的时刻与法兰出现严重起皱的时刻相接近.一般工程认为:贴模旋压过程法兰产生轻微皱纹,通过合理的后续法兰旋出成形是可以消除的;若皱纹无法消除,则认为法兰发生了严重起皱.因此,本文将第一道次贴模旋压发生的、且在第一道次旋出阶段无法碾平的起皱,在第一道次贴模阶段发生的时刻定义为严重起皱发生时刻.为了最大限度消除第一道次贴模旋压时法兰产生的皱纹,采用尽可能平直的旋轮轨迹,如图7(a)所示,对图2中不同成形角的工件继续进行第一道次法兰旋出试验.图7试验结果表明,40° 和45° 法兰旋出时法兰皱纹可以消除,而50° 时法兰皱纹不能消除,这与旋压力曲线的极值点是接近的.因此可以推测:旋压力法可以用于预测严重起皱时刻.

图7 法兰旋出试验Fig.7 Flange spinning-out test
3.3 弹性应变能法
在普旋成形过程中,旋轮给板坯施加的变形力导致了法兰弹性应变能增加和振荡[16].从数值仿真模型中,提取旋压成形过程中变形板料弹性应变能(Es)变化曲线,如图8所示.可以看出:变形板料的弹性应变能随着成形角度的增大而不断增大,但并没有出现明显的波动.因此,对于半球形件第一道次普旋贴模成形过程,并不能以变形板料弹性应变能的振荡来进行法兰起皱的判定.
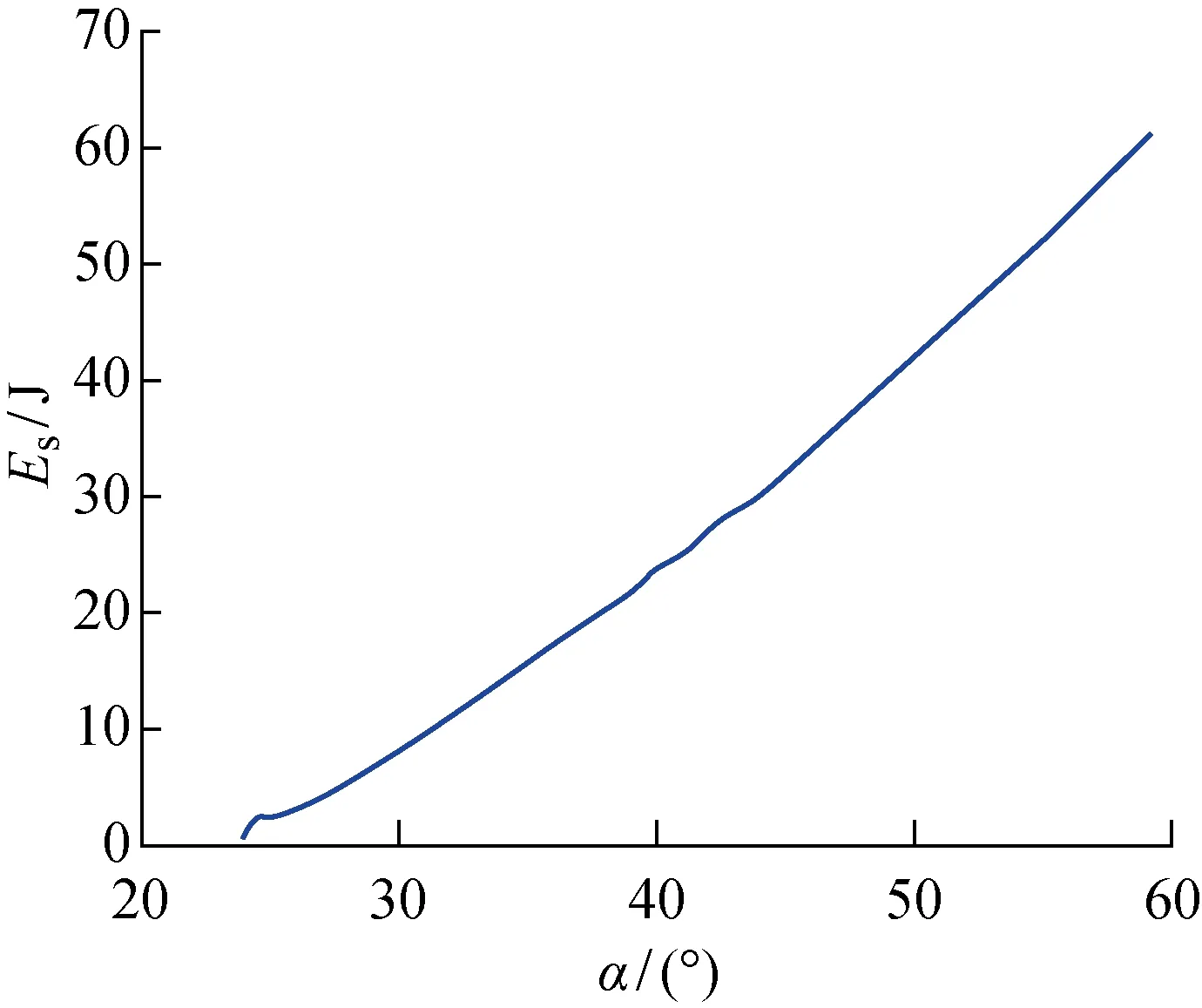
图8 变形板料弹性应变能变化Fig.8 Change of the elastic strain energy
3.4 基于塑性失稳理论的方法
基于能量法和塑性屈曲理论,Kong等[12]建立了旋压法兰平面环失稳数学模型,并利用旋压仿真模型提供更为准确的应力边界条件,实现普旋过程第一道次法兰起皱预测.具体方法为:从数值仿真中法兰应力环上提取最大周向压应力和最大径向应力,通过MATLAB计算出法兰失稳的临界周向压应力.对比同一时刻法兰应力环上最大变形周向压应力和临界周向压应力,若满足前者大于后者,则判断为法兰失稳,此时法兰区发生起皱现象.本研究基于这一预测模型,进行了半球形件旋压法兰起皱现象的评价,其预测结果如图9所示,其中σc为周向压应力.当成形角超过40.6° 时,最大周向压应力大于临界压应力,判断此时法兰产生起皱,滞后试验起皱时刻2.9°,误差为7.7%,与试验结果吻合较好.由于此方法是基于旋压法兰的塑性失稳建立的,该方法适用于预测法兰起皱产生的时刻,而无法预测严重起皱时刻.

图9 基于塑性失稳理论的预测结果Fig.9 Predicted results based on the plastic instability theory
3.5 讨论
与基于塑性失稳理论的方法相比,法兰边缘波动标准偏差和旋压力方法,对数值仿真建模形式和计算精度的要求更高,例如,对于大型薄壁构件旋压过程数值仿真,全模型计算耗时是相当长的,难以满足工程应用,一般采用较大单元尺寸、对称模型假设等途径来缩短计算耗时,这将引起仿真中法兰几何刚度增加,导致了旋压仿真中法兰皱纹形成的延迟,进而影响边缘波动标准差和旋压力这两种方法的评估精度.而对于基于塑性失稳理论的方法,仅需从仿真中提取某母线上的应力应变场和法兰径向几何边界,上述简化模型对这些物理量的影响相对较小,这样,基于塑性失稳理论的方法具有更高的评估精度.
综上所述,在数值仿真中,法兰几何波动和旋压力两种方法在起皱评估上具有便捷性,尤其是小型薄壁构件旋压起皱的评估;而对于采用上述简化仿真模型的大型构件旋压起皱评价而言,建议采用基于塑性失稳理论的方法.
4 结论
对比研究了法兰几何波动、旋压力、弹性应变能振荡和基于塑性失稳理论的起皱模型这4种方法对旋压法兰起皱发生时刻预测的适用性,得出了以下结论:与2024-O铝合金球面薄壁构件第一道次普旋试验对比显示,法兰几何波动和基于塑性失稳理论的起皱模型均可以预测旋压法兰起皱发生时刻,其中基于塑性失稳理论的起皱模型具有更小的预测误差;旋压力和弹性应变能振荡不能准确预测出法兰起皱发生时刻;旋压力法可以预测法兰严重起皱时刻.

