一种新型灵巧枪弹的气动特性研究

周磊， 李忠新， 杨海波， 蔡红明

(南京理工大学 机械工程学院, 江苏 南京 210094)

0 引言

现代战争对自动武器系统提出了更高的精度要求，枪弹射击精度直接影响着单兵的战斗力和生存能力，因此提高枪弹射击精度成为自动武器领域的重要方向之一[1]。由于材料、工艺等方面的限制，难以大幅度提高传统枪弹[2]的射击精度，特别在射击环境、自身因素等发生变化时，普通射手难以精确打击目标。近年来，随着集成电路和微机电系统(MEMS)技术的发展，研制可自动调节误差的灵巧枪弹成为提高枪弹射击精度的有效途径。

对于灵巧枪弹的设计与研发，国内外作了相当多的研究。Lawhorn等[3]发明了一种通过控制阀门开合提供控制力矩的灵巧枪弹，该枪弹速度降较大，且难以大规模生产。Barrett[4]研究了一种通过压电陶瓷材料偏转弹头提供控制力矩的身管发射式自适应枪弹，该枪弹设计新颖，但控制力矩偏小。Barrett等[5]设计了一种通过压电材料形变驱动尾翼变形的灵巧枪弹，该枪弹难以实现精确控制且控制力矩小。Jones等[6]设计了一种基于激光半主动制导和尾翼偏转控制的灵巧枪弹，并于2012年进行了实弹测试。

长期以来，对弹丸气动特性的研究通常有以下4种方法：工程估算[7]、风洞实验[8-9]、参数辨识[10-11]和数值仿真[12-16]。其中，工程估算是最为简单快捷的方法，而风洞实验是最为精确的方法，参数辨识则是基于理论与实验对数值结果进行预测的一种方法。进入21世纪以来，计算流体力学的快速发展使得数值仿真成为模拟和研究枪弹流场的主要手段，其不仅能有效缩短研究周期，还能保证一定的精度要求。吴志林等[17]设计了一种尾翼折叠式修正枪弹，并采用数值仿真方法研究了该枪弹的气动特性。高炳龙等[18]设计了一种可控枪弹的结构，并利用计算流体力学软件Fluent研究了该枪弹的气动特性。对于外形尺寸变化对灵巧枪弹的气动特性影响，国内外还鲜有相关文献发表。

本文考虑器件尺寸和气动特性的技术要求，设计了一种新型增程灵巧枪弹的气动外形。采用数值仿真和风洞实验方法分别得到枪弹各气动仿真参数和气动实验参数，验证了所用数值仿真方法的可行性，并结合该数值方法分析了收缩段长度、交界半径和弹底半径等弹尾外形尺寸变化对灵巧枪弹气动特性的影响规律。

1 灵巧枪弹总体方案

本文研究的是一种新型12.7 mm口径灵巧枪弹的气动特性，其实弹弹尾布置有执行机构，内部有制导系统、能源系统等部件。采用滑膛枪管发射，通过尾翼保持枪弹飞行稳定性，并通过尾舵控制枪弹飞行轨迹，弹丸出膛后弹托自动脱落。该灵巧枪弹采用激光半主动制导方式，在枪弹飞行过程中激光指示器持续照射目标，弹载激光导引头接受目标漫反射信号，弹载计算机判断弹目相对位置，计算并发送控制信号给舵机修正弹道，直至命中目标。该灵巧枪弹结构包括弹尖、截锥段、圆柱段、收缩段和扩张段、尾翼等部分，如图1所示。

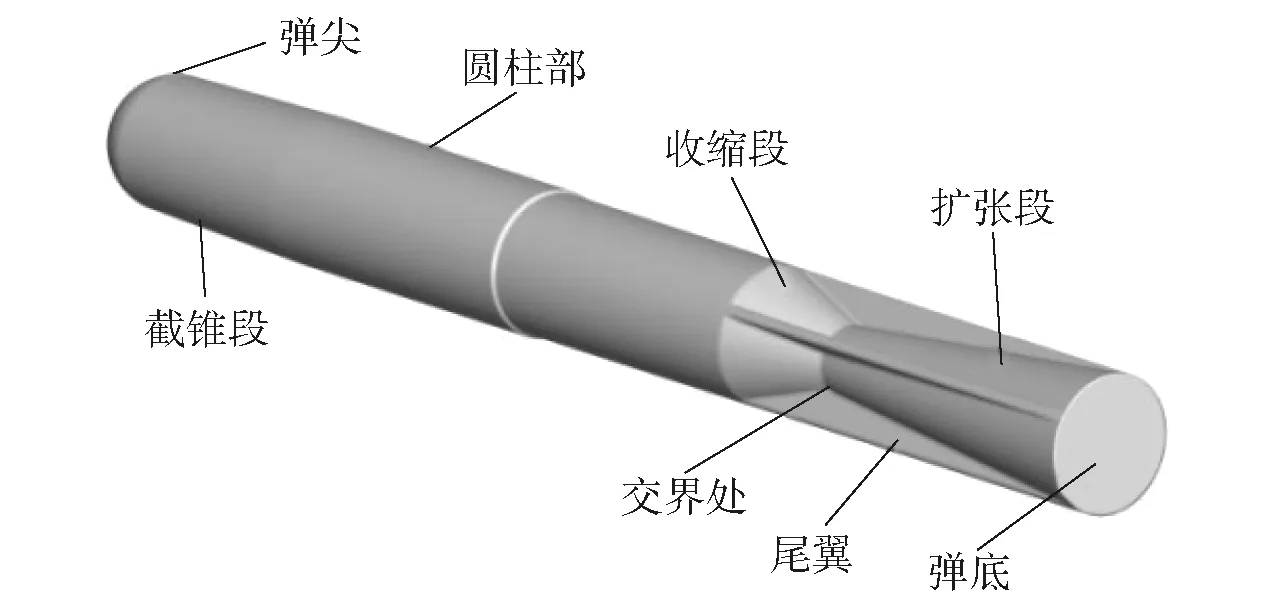
图1 灵巧枪弹三维图Fig.1 3D diagram of smart bullet

综合考虑灵巧枪弹内外弹道性能、终点效能、器件可靠性和人机功效，本文设计的灵巧枪弹总体参数如表1所示。

表1 灵巧枪弹总体参数Tab.1 General parameters of smart bullet

由于导引头尺寸限制，灵巧枪弹弹尖设计成半圆形。同时，为布置尾翼并保证灵巧枪弹飞行静稳定性，灵巧枪弹尾部设计成收缩-扩张段。取枪弹弹轴为x轴，方向由弹尖指向弹底，y轴取为竖直向上，z轴由右手定则得到，原点取弹尖顶部。灵巧枪弹各部分尺寸如图2所示。

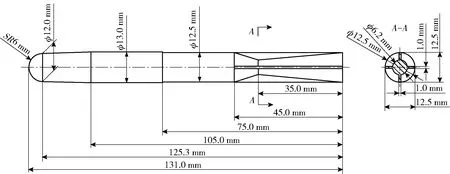
图2 灵巧枪弹二维图Fig.2 2D diagram of smart bullet

2 风洞实验

2.1 实验模型与设备

由于研究的灵巧枪弹尺寸较小、不利安装，本文按照4∶1的比例加工制作全金属灵巧枪弹刚性模型，模型全长524 mm，最大直径52 mm.

为验证数值计算的准确性，在FL-23型风洞中进行了样弹模型风洞实验研究。FL-23型风洞是一座直流暂冲式跨超声速风洞，该风洞实验段横截面尺寸为0.6 m×0.6 m，实验段长2.5 m，零攻角时模型在FL-23型风洞中的堵塞度约为0.59%. 风洞马赫数Ma范围为0.40～4.50，实验控制精度为±0.003，实验段核心流马赫数的均匀性等其他性能指标均满足GJB1179—1991高速风洞与低速风洞流场品质规范要求。采用六分量应变天平配合天平支杆测量模型上的气动力，实验模型采用尾支撑方式安装于风洞机构上，如图3所示。

图3 灵巧枪弹风洞实验示意图Fig.3 Schematic diagram of wind tunnel experiment

六分量应变天平型号为2N6-18A，静校结果如表2所示，其中Fx、Fy和Fz表示3个方向的分力，Mx、My和Mz表示3个方向的分力矩。灵巧枪弹风洞实验的Ma为0.5、0.7、0.9、1.0、1.2、1.5、1.8、2.0，实验迎角组合为-4°、-3°、-2°、-1°、0°、1°、2°、3°、4°. FL-23风洞使用PXI数据采集系统，总通道数为64，信号采样速率100 kS/s，分辨率16 Bit，用于采集风洞中天平输出的仪表信号，天平输出为电压信号。数据处理计算机对实验数据进行处理，实时提供实验数据。

2.2 实验结果

图4为灵巧枪弹静态气动阻力系数随攻角变化曲线。由图4可以看出，随着马赫数的增加，阻力系数先逐渐增大，在Ma=1.5时达到最大，之后阻力系数又逐渐小幅度降低。本文研究的灵巧枪弹阻力系数较大，这是综合考虑内部器件尺寸和静稳定性等技术要求的结果。

表2 六分量天平精校结果Tab.2 Accurate alignment of six-component balance

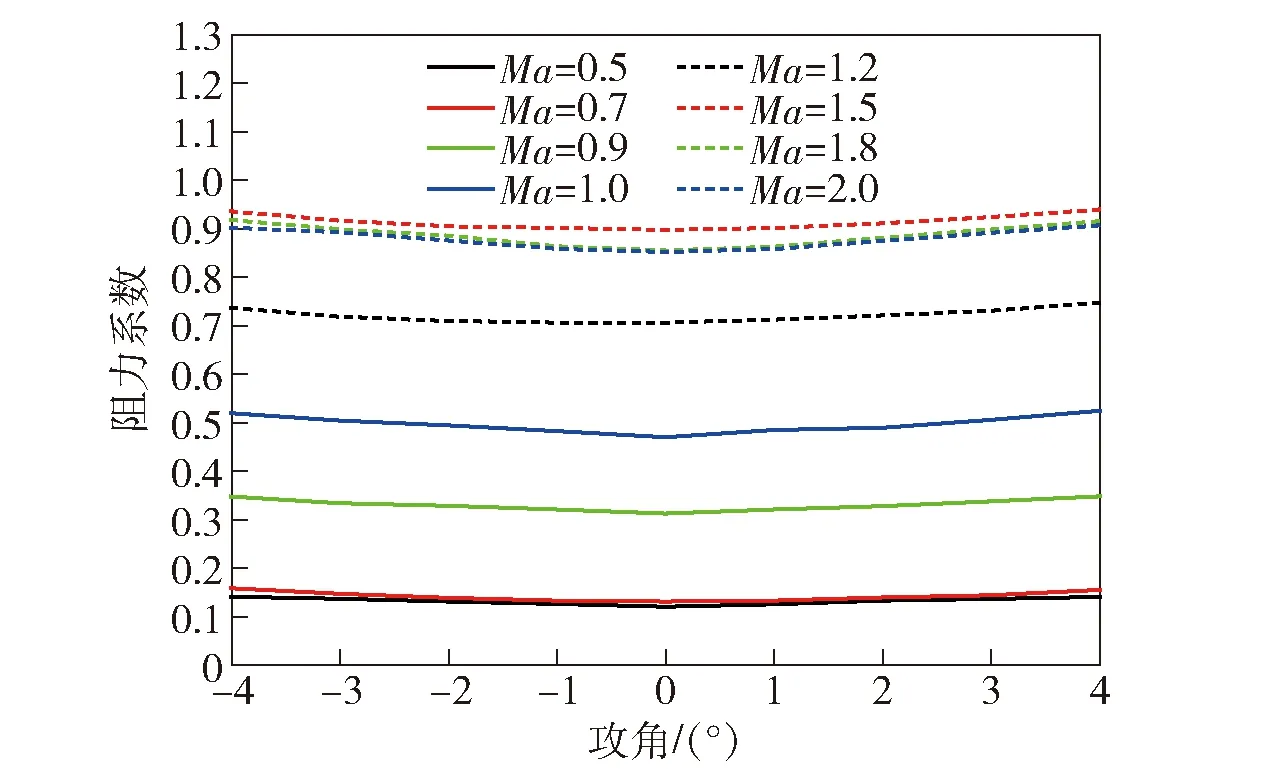
图4 灵巧枪弹阻力系数实验曲线Fig.4 Experimental drag coefficient vs. angle of attack

图5为灵巧枪弹静态气动升力系数随攻角变化曲线。由图5可以看出，随着攻角的增大，升力系数逐渐增大。在Ma=0.70时灵巧枪弹升力系数最低，在Ma=2.00时升力系数最高。总之，灵巧枪弹的升力系数与攻角近似呈线性关系，而与飞行马赫数相关性较低。

图5 灵巧枪弹升力系数实验曲线Fig.5 Experimental lift coefficient vs. angle of attack

图6为灵巧枪弹静态俯仰力矩系数随攻角变化曲线。由图6可以看出，随着攻角的增大，灵巧枪弹的俯仰力矩系数绝对值(正攻角时，静态俯仰力矩系数为负即静稳定)逐渐增大，在实验范围内，灵巧枪弹纵向静稳定。与升力系数类似，灵巧枪弹静态俯仰力矩系数与飞行马赫数相关性较低。

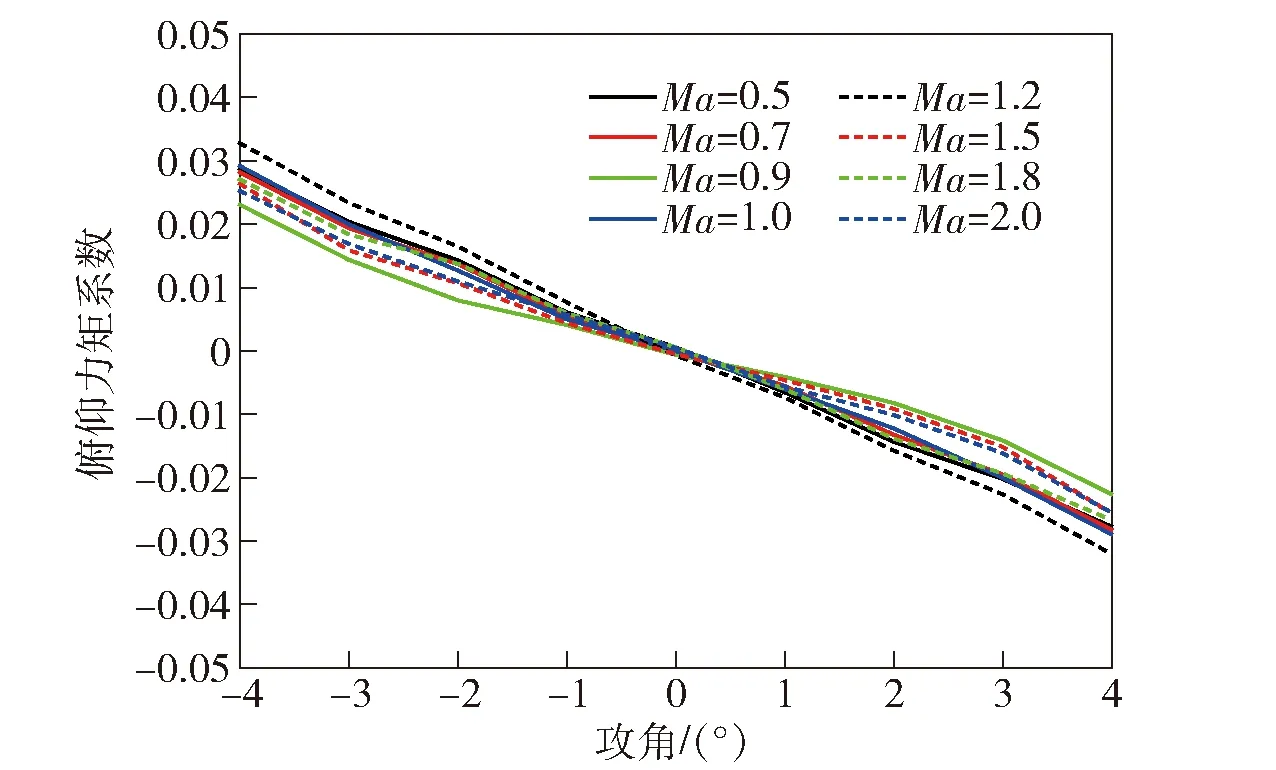
图6 灵巧枪弹俯仰力矩系数实验曲线Fig.6 Experimental pitch moment coefficient vs. angle of attack

3 数值模拟方法

3.1 控制方程和离散方法

相对于不守恒控制方程，守恒控制方程可以更好地保证流场物理参数的守恒。本文采用以下动量、质量和能量守恒雷诺平均纳维-斯托克斯(RANS)方程作为控制方程[19]：

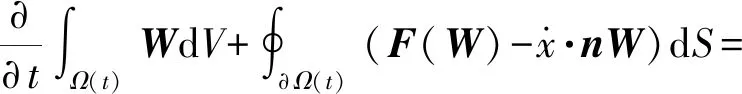
(1)

本文对流场控制方程和湍流模型分别离散求解，采用SIMPLEC格式求解压力-速度耦合方程，采用2阶迎风格式离散求解控制方程，采用3阶MUSCL格式离散求解湍流模型。

3.2 湍流模型

湍流模型对于准确模拟非定常复杂流动至关重要，本文采用Menter[20]提出的两方程剪切压力传输(SST)k-ω湍流模型封闭控制方程，k和ω分别为湍流动能和湍流比耗散率。该湍流模型考虑到了湍流剪切应力的传播，较标准k-ω模型有更好的模拟精度：

(2)

式中：下标i、j表示不同方向的分量；Γ、Γk和Γω为扩散率；u、ρ和p分别为速度、密度和压强；Gk和Gω为湍动能及比耗散率的增加项；Yk和Yω为湍动能及比耗散率的减少项；Dω为比耗散率扩散项；Si、Sk和Sω为速度、湍动能及比耗散率的源项。

4 灵巧枪弹气动特性研究

4.1 计算网格

图7为灵巧枪弹周围流场的计算网格示意图。对于本文设计的灵巧枪弹模型，其尾部外形布局相对复杂，使得其对周围流场的扰动机理较为繁复，尾部外形对枪弹气动特性的影响也较为重要。因此，对枪弹尾部进行适当网格加密。计算域取为圆柱流场，长为2 000 mm，半径为900 mm，枪弹表面划分有附面层，附面层第1层厚度d=6.3×10-7m，增长率为1.1，附面层数为20. 枪弹表面到压力远场边界网格增长率为1.1，网格数量约为620万。

图7 灵巧枪弹周围计算网格Fig.7 Computational grids around smart bullet

4.2 数值模拟方法验证

图8为灵巧枪弹基准弹形数值仿真结果和风洞实验结果对比图。从图8(a)可以看出，在不同马赫数下，阻力系数仿真结果均略大于风洞实验结果。在Ma=0.90时，计算误差较大，阻力系数最大误差率为16%；在其他马赫数下，阻力系数最大误差率为6.3%. 从图8(b)可以看出，在不同马赫数下，升力系数仿真结果整体略小于风洞实验结果，升力系数最大误差率为16.6%. 在小攻角下，计算误差相对较大，其原因可能与模型安装精度有关。总之，灵巧枪弹气动特性的数值仿真结果和风洞实验结果基本一致，证明了本文数值模拟方法的有效性。

图8 灵巧枪弹基准弹形仿真与实验结果对比Fig.8 Comparison of simulated and experimental results

4.3 收缩段长度对气动特性影响

本文以基准弹形为基础，保持枪弹总长、尾部总长不变，将收缩段分别增长5 mm、10 mm、20 mm和30 mm，得到4种新弹形，进而计算分析Ma=1.5下各弹形的气动参数变化及周围流场变化。表3为灵巧枪弹在不同收缩段长度下的气动参数计算结果。由表3可见，随着收缩段长度的增大，灵巧枪弹阻力系数先减小、后增大，升力系数先基本保持不变、后增大，俯仰力矩系数绝对值同样先基本保持不变、后增大。收缩段长度越大，对灵巧枪弹稳定性越有利，但由于扩张段需布置舵机和增程发动机，因此本文设计的灵巧枪弹收缩段长度较小，在舵机和增程发动机尺寸有突破的情况下，可将灵巧枪弹收缩段长度适当加长。

图9为Ma=1.5、α=0°时5种弹形收缩段和扩张段气动阻力变化曲线图。由图9可见：当收缩段长度小于一定值时，收缩段对气动阻力的影响占主导，其气动阻力随收缩段长度增加而减小；当收缩段大于一定值时，扩张段对气动阻力的影响占主导，其气动阻力随收缩段长度的增加而增大。

表3 灵巧枪弹在不同收缩段长度下的气动特性Tab.3 Aerodynamic characteristics for different lengths of contraction section

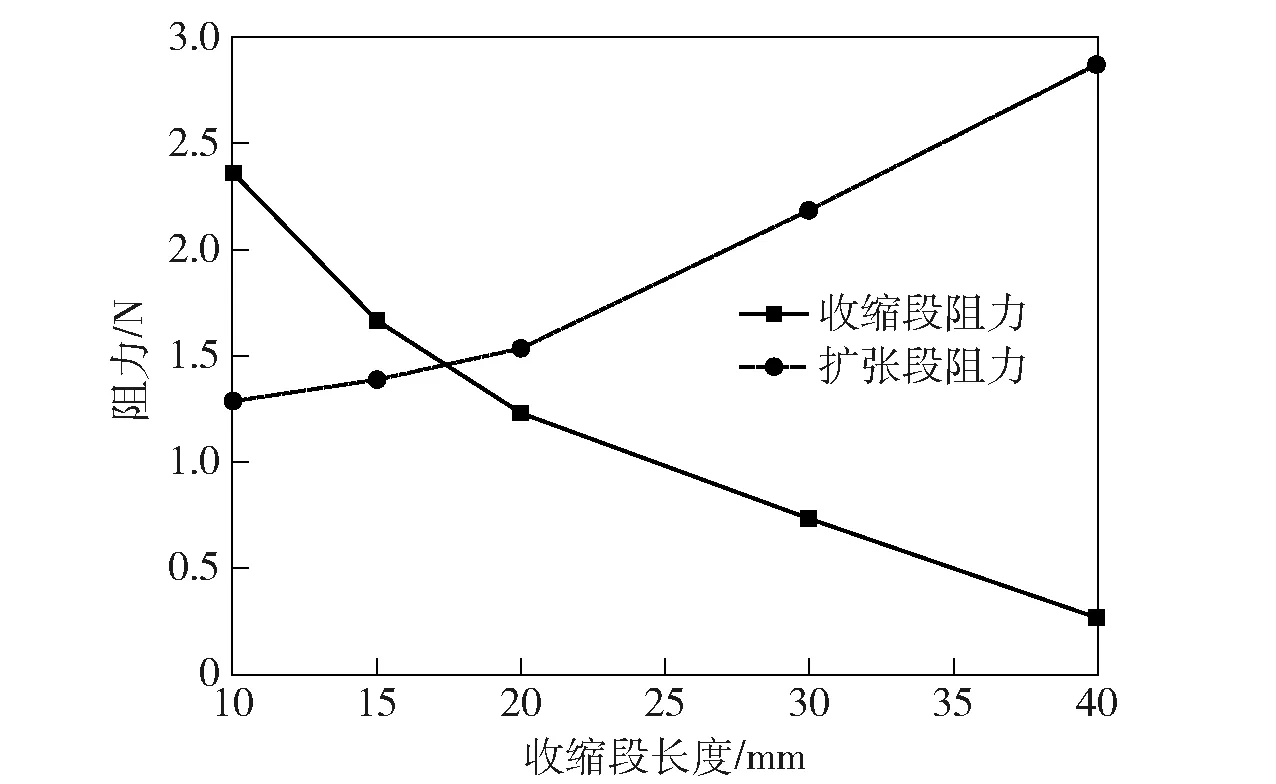
图9 收缩段和扩张段表面阻力变化曲线Fig.9 Surface drag curves of contraction and dilatation sections

图10 4种收缩段长度下灵巧枪弹表面压力分布Fig.10 Pressure distribution on bullet surface for different lengths of contraction section

图10为Ma=1.5、α=2°时4种不同弹形收缩-扩张段上下表面压力分布曲线图。为了避开尾翼，本文所取截面与纵平面存在小角度β(sinβ=0.2)。由图10可见：在灵巧枪弹收缩段前半部产生负升力，在收缩段后半部及扩张段产生正升力；随着收缩段长度的增加，由负升力变为正升力的转折点逐渐后移。由于弹尾收缩-扩张结构的存在，气流在弹尾收缩段表面发生流动分离，在扩张段表面发生再附，并在交界处产生涡流；随着收缩段长度的增加，流动分离被推迟，流动再附被提前，收缩-扩张段上下表面压力分布发生剧烈变化，上下表面压差明显增大。综上所述，灵巧枪弹升力特性随收缩段长度呈现复杂的变化规律。

4.4 交界半径对气动特性影响

本文以基准弹形为基础(交界半径ra为3.1 mm)，将收缩-扩张段交界半径分别减小0.5 mm、1.0 mm和增大0.5 mm，得到3种新弹形。表4为在4种交界半径下，灵巧枪弹的气动参数计算结果。由表4可知，随着交界半径的增大，灵巧枪弹阻力系数与升力系数减小，俯仰力矩系数绝对值减小，灵巧枪弹的纵向静稳定性减弱。

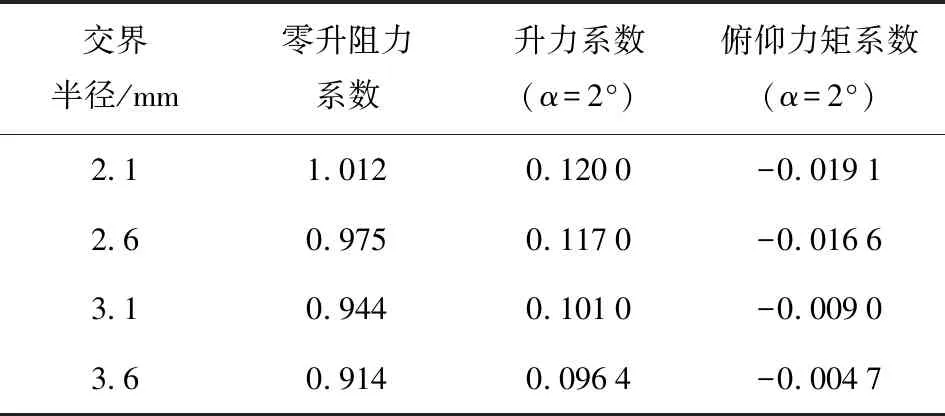
表4 灵巧枪弹在不同交界半径下的气动特性Tab.4 Aerodynamic characteristics for different radii of intersection

图11分别为Ma=1.50、α=2°时4种不同交界半径ra的灵巧枪弹收缩-扩张段截面压力云图与流线图。由图11可见，随着交界半径的增大，收缩段表面压强逐渐升高，扩张段表面压强逐渐减少，从而减少了灵巧枪弹的阻力。从图11中还可以发现，随着交界半径的增大，收缩-扩张段交界处的流动逐渐平缓，涡强度逐渐减小。这是因为交界半径的增加使得收缩段和扩张段坡度变缓，流动的分离及再附效应加强，交界处的涡逐渐沿轴向向内收拢，涡强度逐渐减小，耗散的能量减少，产生的气动阻力越小。

图11 4种不同交界半径下灵巧枪弹收缩-扩张段的截面压力云图和流线图Fig.11 Pressure contour and streamline of contraction and dilatation sections for different radii of intersection

图12为Ma=1.50、α=2°时4种不同交界半径的灵巧枪弹尾部上下表面压力分布曲线图。由图12可见，相比于收缩段长度的变化，交界半径变化对升力的影响较为直观。随着交界半径的增加，由负升力变为正升力的转折点逐渐后移，收缩-扩张段升力减小。交界半径的增大减少了水平舵面的面积，尾翼提供的升力减小。二者相加，总的升力逐渐减小，同时其纵静稳定性也逐渐减弱。

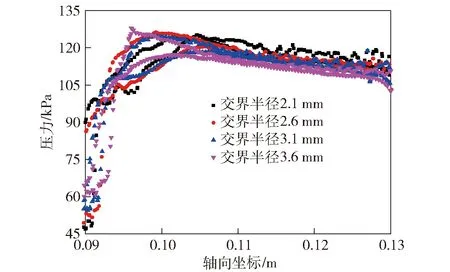
图12 4种不同交界半径下灵巧枪弹表面压力分布Fig.12 Pressure distribution on bullet surface for different radii of intersection

4.5 弹底半径对气动特性影响

本文以基准弹形为基础(弹底半径rb为6.25 mm)，将弹底半径分别减小0.60 mm、1.20 mm和1.80 mm，得到3种新弹形。表5为4种弹底半径下，灵巧枪弹的气动参数计算结果。由表5可知，随着弹底半径的减小，灵巧枪弹零升阻力系数减小，升力系数先略微增大后减小，俯仰力矩系数绝对值先略微增大后减小。

图13分别为Ma=1.5、α=2°时4种不同弹底半径rb的灵巧枪弹底面压力云图。由图13可见：随着弹底半径的减小，枪弹底面压强升高，枪弹阻力减小；在枪弹底面，中心位置为压强最高处，沿半径增大方向压强逐渐降低，当达到最低值时压强又逐渐回升；由于攻角的存在，枪弹底面上部压强低于下部压强。

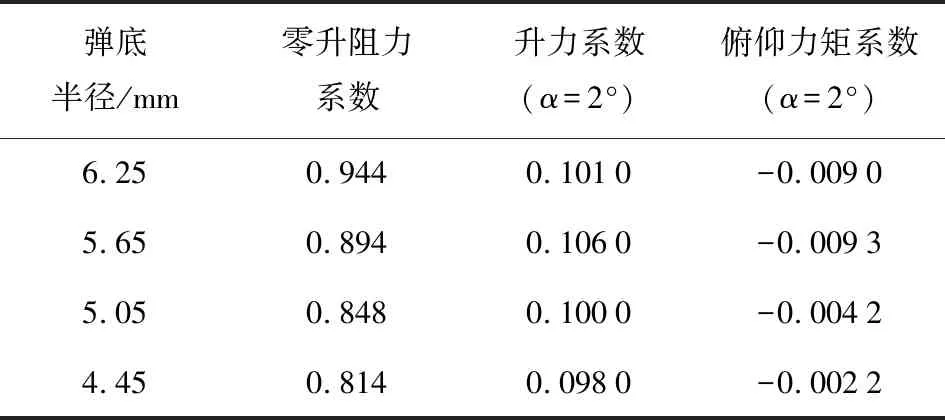
表5 灵巧枪弹在不同弹底半径下的气动特性Tab.5 Aerodynamic characteristics for different radii of bottom

图13 4种不同弹底半径下灵巧枪弹底面压力云图Fig.13 Pressure contour of bottom under different radii of bottom

图14分别为Ma=1.5、α=2°时4种不同弹底半径的灵巧枪弹尾端截面压力云图和流线图。由图14可见，由于攻角的存在，枪弹底面处产生非对称的底涡，并且上方的涡要强于下方的涡，但下方涡的面积要大于上方的涡。弹底涡越强，弹底表面压强就越低，与底面压力云图结论一致。随着弹底半径的减小，弹底涡的强度逐渐减弱，压强逐渐增加，因此阻力减小。同时，随着弹底半径的减小，扩张段上下表面压差减小，所提供的升力减小。但由于水平舵面积的增大，舵面提供的升力增大，全弹升力变化比较复杂。

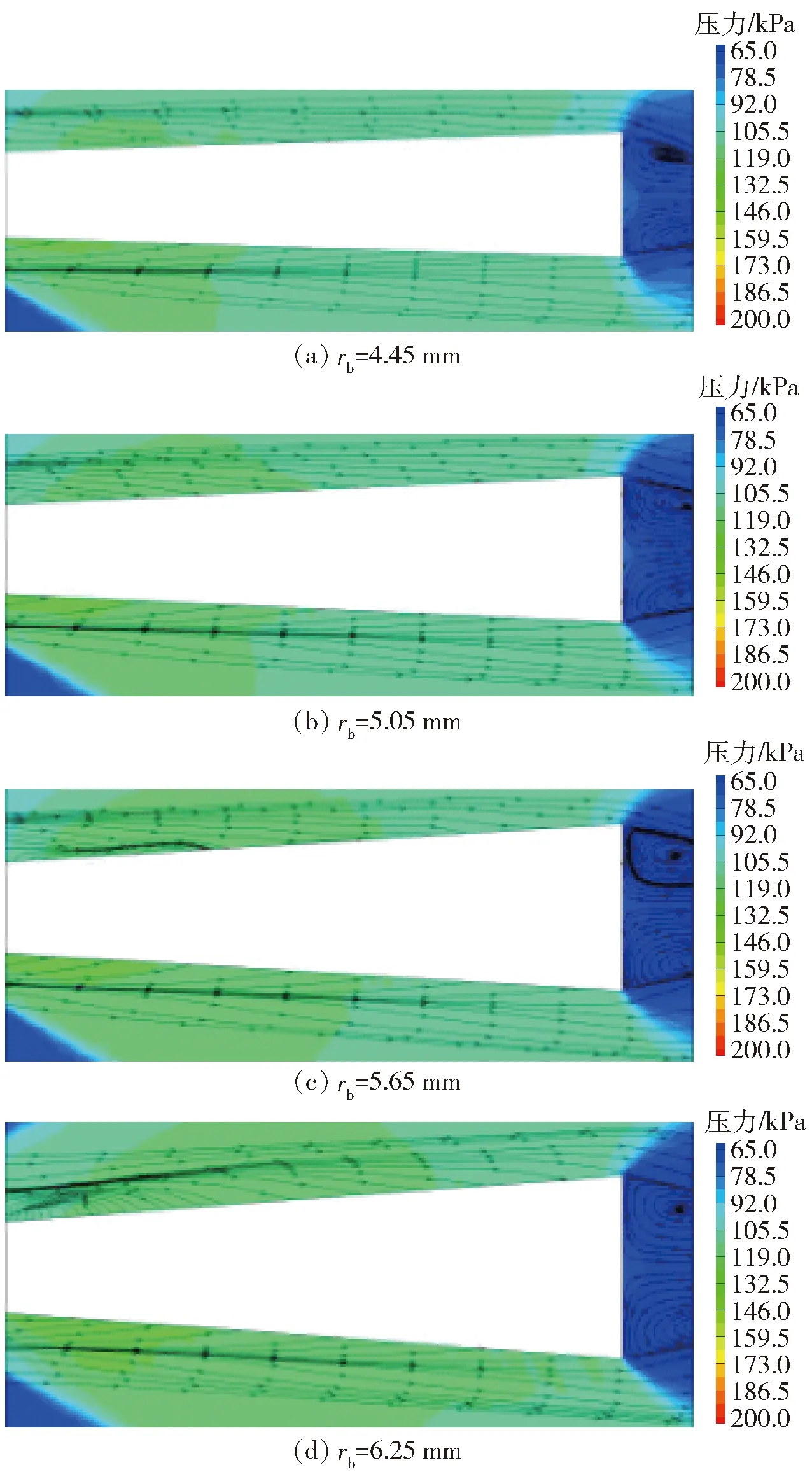
图14 4种不同弹底半径下灵巧枪弹尾部截面压力云图和流线图Fig.14 Pressure contour and streamline of bullet tail for different radii of the bottom

5 结论

本文考虑器件尺寸和气动特性的技术要求，设计了一种新型增程灵巧枪弹的气动外形。采用数值仿真和风洞实验的方法研究了灵巧枪弹的气动特性，并分析了弹尾外形尺寸变化对灵巧枪弹气动特性的影响规律。得到了以下结论：

1) 数值仿真结果和风洞实验结果基本一致，证明了数值仿真方法的可行性。随着马赫数的增加，阻力系数先逐渐增大，在Ma=1.5时达到最大，之后阻力系数逐渐小幅度降低。升力系数与攻角近似呈线性关系，而与飞行马赫数相关性较低。随着攻角的增大，灵巧枪弹的俯仰力矩系数绝对值逐渐增大，而与飞行马赫数相关性较低。

2) 随着收缩段长度的增加，收缩段和扩张段对气动性能起着相反的影响效果。收缩段处阻力和升力减小，而扩张段处阻力和升力增大。

3) 随着交界半径的增大，阻力、升力和俯仰力矩绝对值均明显减小。

4) 随着弹底半径的增大，阻力先增大后减小，升力和俯仰力矩绝对值先减小后增大。弹底半径的减小会增大水平舵的面积，因此弹底半径变化对升力影响较为复杂。