基于随动边界的火炮身管热力联合效应数值分析

于情波， 杨国来， 葛建立

(南京理工大学 机械工程学院, 江苏 南京 210094)

0 引言

现有火炮对大口径、大威力以及远射程的要求使身管处于更严峻的工作环境，身管胀膛、炸膛以及断裂等事故时有发生[1-2]。因此，用现代计算方法对射击环境下的身管动态响应进行研究，具有重要的意义。在实弹射击过程中，身管受载来自于炮架接触力、火药气体作用力、弹丸接触力以及后坐惯性力，其中火药气体作用力被认为是主要作用压力。传统设计理论考虑的身管受载边界条件过于简化，与实际身管动态响应具有较大差别。侯健等[3]指出传统上采用的弹性强度失效准则未能代表火炮身管失效的本质，并提出了一种允许小塑性变形发生在身管内膛公差范围内的强度设计方法，但该方法同样建立在静力作用下厚壁圆筒理论的基础上，并没有顾及身管材料的动态受载。谈乐斌等[4]指出了身管静强度设计理论的不足，并借助有限元仿真软件ANSYS建立了非线性厚壁圆筒有限元模型，采用分步加载的方式模拟时变受载过程，计算分析了材料动应力响应结果，但该计算模型被简化为轴对称平面应变问题，与实际载荷空间分布具有一定差异。实际射击过程中，火药燃气压力值与其作用区域具有时变特性，弹后身管受载区域根据弹丸实时运动位置而动态变化，曾志银等[5]运用有限元仿真软件ANSYS提供的APDL语言定义了身管径向动态受载的类型，计算得到了相应的动态应力结果。但该动态设计理论仅适用于身管特定横截面，并不能得到整个射击过程对应的身管整体刚度和强度(简称刚强度)变化规律。

上述文献计算身管动力学响应时，仅考虑了气体压力效应，而忽略了高温效应对材料力学响应的影响。射击过程中火药气体温度可以达到2 800 K，与身管内壁形成强烈的对流热交换,使得内壁升温可以达到1 000 K以上，Chung等[6]指出身管烧蚀磨损主要由火药气体热效应产生，并且多发连击后身管内膛累积残留热量会对弹药以及士兵带来严重的安全隐患。因此，探索实弹射击过程中身管瞬态热响应特性，对研究其材料动态响应规律以及宏微观烧蚀磨损机理具有重要意义。文献[7]采用有限差分方法对小口径火炮身管的温度分布特性进行了计算，并分析了单发及连发射击条件下温度场的分布及其变化规律。朱文芳等[8]研究了某火炮连续发射过程中的身管传热规律，并对不同射击工况下身管径向温度分布进行了计算分析。文献[9]针对大口径火炮身管温度响应以及水流冷却对身管温度分布的影响进行了计算分析。身管在空间域内形成的不均匀温度梯度引起的结构非均等热膨胀势必带来一定程度的热应力响应。文献[10-11]在温度响应分析的基础上，以非均布温度场为条件对身管进行了热力耦合分析，得到了瞬态热应力场分布规律。但现有的很多文献在研究身管温度场以及热应力场时，大多将其简化为不考虑轴向传递的径向一维热传导物理模型，与实际三维模型存在较大差别。实际射击过程中，高温气体与身管内壁之间的强对流换热边界条件随弹丸运动而动态变化，轴向不同位置横截面承受的热冲击过程存在较大差异。胡志刚等[12]在对某口径火炮身管温度及热应力场进行有限元数值分析时，通过数据表的形式控制随弹丸位置以及作用时间而动态变化的热对流边界，该方法需要大量的建模工作，并且不能准确表达随时间连续变化的边界情况。上述文献得到的计算结果表明，身管内壁局部区域分布的热应力甚至可以达到材料屈服极限，热载荷在身管刚强度响应方面同样具有不可忽视的作用。纵观现有文献，综合考虑身管内部压力载荷和热载荷联合作用，对身管结构刚强度进行分析的工作开展得较少。徐亚栋等[13]采用有限元分析方法计算分析了复合材料身管在压力载荷和热载荷联合作用下的刚强度结果，但该边界条件同样没有考虑随动过程。

本文综合考虑了火药气体热载荷以及压力载荷对身管动态应力响应的影响，借助有限元软件建立了身管三维瞬态热力耦合模型，通过子程序接口成功模拟了载荷边界随弹丸运动而变化的动态过程，由顺序热传导-热应力耦合分析方法得到了不同时刻对应的身管温度场以及温差应力的分布规律，并进一步分析了热冲击载荷以及压力载荷对身管强度的影响。

1 火药燃气热力联合效应数学模型

内弹道时期，身管弹后区域为火药燃气作用区域，身管结构力学响应主要取决于气体压力以及高温效应的影响。膛内气体压力垂直作用于身管内表面，同时高温效应与内壁之间以热对流的方式进行热量传递，在身管内部以热传导的方式进行热量传递，热场作用得到的非均匀温度分布导致各质点出现不同的热膨胀，进而产生一定的温差应力。图1为火药气体动态作用效能示意图，其中p(x,t)、T(x,t)分别为t时刻对应的压力载荷以及热冲击载荷，Δt为时间增量。弹后空间随弹丸轴向移动而逐渐扩张，冲击载荷作用边界随之而动态平移，即作用区域取决于弹丸膛内运动位置。另一方面，冲击载荷幅值是随时间变化的非定常值。

图1 火药气体作用边界随动过程示意图Fig.1 Follow-up process of gas loading boundary

1.1 身管径向受载力学模型

后坐惯性力、炮架接触力、弹丸碰撞力以及火药燃气压力等作用效能激励身管产生一定的弹性变形，将引起身管横向振动，并对身管强度具有直接影响。其中，火药气体的径向压力为身管强度校核的主要依据，火药燃气压力作用区域随弹丸运动位置而动态变化，同时其幅值随时间而变化。假定身管轴向方向为笛卡尔坐标系x轴，身管尾端面中心点为坐标原点，则身管在时域内的作用力可近似表述为

F=∑ξ(x-st)p(x,t)ds，

(1)

式中：x为身管内壁积分点轴向坐标；st为t时刻弹丸距膛底的距离；ξ(x-st)为作用于身管内壁的燃气压力随弹丸运动而变化的函数，

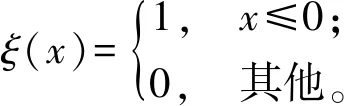
(2)

基于拉格朗日模型，假设得到的气体压力分布作为弹后空间身管内壁的载荷分布，弹后空间气体压力呈抛物线分布：

(3)

式中：φi为仅考虑弹丸旋转运动和摩擦功的次要功系数；ω为装药质量；m为弹丸质量。

在任意身管横截面，其应力响应取决于气体压力，由拉梅公式[14]可知，平面应变假设下身管任一质点应力分量可表示为

(4)

式中：τ、θ、z分别表示径向、周向和轴向分量；p(t)为t时刻压力；b为身管外径；a为身管内径；r为身管截面任意半径；ν为泊松比。

1.2 身管温度场物理模型

火炮发射过程伴随着复杂的热场变化过程，高温火药燃气与身管内壁的瞬态强制热对流造成身管温升。火炮射击过程中，内膛传热以传导、对流和辐射3种方式进行。文献[11]指出辐射换热量约为对流换热量的1%，因此本文忽略热辐射的影响。身管温度场物理模型可表示为：

1) 高温气体与内膛的强制对流热交换属于瞬态温度场，膛内三维传热微分方程为

(5)

式中：ρ为材料密度；cT为材料比热；T为温度；Q为热源强度；kx、ky、kz分别为x轴、y轴和z轴3个方向的热传导系数。

2) 边界条件。内弹道时期身管表面与火药燃气以及外部环境形成对流换热，以温度场第3类边界条件表达。

内边界条件为

(6)

外边界条件为

(7)

式中：nx、ny、nz分别为边界外法向的方向余弦；hi、ho分别为内、外热对流系数；Tg、T∞分别为火药燃气温度以及环境温度。

在利用有限元方法求解微分方程时，空间离散域内的温度可以由节点温度插值得到，即

(8)

式中：Ni为节点形函数；Ti为节点温度。

离散后的瞬态温度场有限元方程为

(9)

式中：KT为温度刚度矩阵；CT为瞬态变温矩阵；PT为节点热载荷向量。

稳态条件下温度沿径向的分布可以用对数定律进行表示：

(10)

身管内部不均匀的热分布通过材料热膨胀特性对身管结构动态响应造成一定的影响，产生一定的热应力，因此温度不均匀分布导致的厚壁圆筒热弹性应力可表示为

(11)

1.3 物理场边界条件的确定

依据经典内弹道零维模型，假定弹后内膛空间处于热力学平衡状态，物理参数在空间域均匀分布，仅随时间变化，热力学平衡方程为

ωψf/θi=ΔEi+Er，

(12)

式中：等式左边反映了火药燃烧所释放的总能量，ψ为火药已燃百分比，f为火药力，θi为热力指数；ΔEi为火药气体内能减少量；Er为火药气体的状态势能。

(13)

(14)

式中：φ为计及所有次要功的计算系数；v为弹丸轴向速度；S为身管横截面面积；p为平均压力；l0为药室容积缩径比；lt为弹丸位移；T1为火药燃烧当量温度，RiT1=f，Ri为单位质量火药的气体常数，将T1=f/Ri代入(13)式可得Tt的表达式为

(15)

进一步整理后可得

(16)

式中：Te为火药气体爆温，一般取值为2 800 K.

同样地，由(14)式可得平均压力的表达式为

(17)

借助经典内弹道理论，并采用龙格-库塔法对内弹道物理过程进行求解，火药燃烧的物理模型由其辅助方程进行表述：

(18)

(19)

式中：Z1为相对燃烧厚度；μ1、e1、ni为火药相关的燃烧参数；Δt为积分时间步长；χ、λ、μ为火药形状参数。

2 动力学模型建模

以某大口径滑膛炮身管为例，借助有限元分析软件Abaqus对其进行离散化建模，并施加对应的热力联合边界条件，对其动力学过程进行数值模拟。数值模型的建立基于如下基本假设：

1) 在给定的任意时刻，弹后任意截面火药气体参数相等，不考虑其三维空间分布不均匀性，未燃尽的火药颗粒同样均匀分布于弹后空间。

2) 弹丸与内壁的相互作用对身管力学特性具有一定的影响，但其作用是局部的，而且缺乏适当的工程计算方法求解其数值，为分析瞬时高温燃气对身管力学特性的影响，本文不考虑弹丸与身管之间的物理作用过程。

3) 首发射击时，身管内膛表面温度为初始室温。以弹带挤进膛线时刻为起始时刻，火药气体压力设定为30 MPa.

4) 内弹道时期，高能火药燃气主要由强制对流换热的方式将有效热能传递给身管，火药气体与身管内壁之间的热对流系数与二者之间的温度差相关。参阅文献[11]涉及的大口径火炮膛内对流换热系数计算方法，依据马蒙托夫经验公式，将该系数定义为与温差相关的时变参量。

2.1 实体离散建模

依据身管三维形貌以及实际结构尺寸，主要采用六面体热弹耦合减缩积分单元(C3D8RT)对其进行离散化建模，整个模型含有377 520个单元以及380 450个节点。身管采用炮钢材料PCrNi3MoVA，高温火药燃气以对流换热的方式加热身管，使得其物性参数发生变化。为计算方便，材料采用常物性假设，相关材料参数不随温度变化，对应的材料参数如表1所示。

表1 数值模型对应的材料参数Tab.1 Material parameter values for numerical model

身管应力、应变场取决于非均匀分布温度场，而应力、应变场不影响温度场，故采用顺序热弹耦合的热应力分析方法，首先通过传热分析计算身管内部温度场分布，进而通过结构分析得到热应力结果。整个动力学数值模型采用Abaqus/standard软件进行求解。

2.2 边界条件建模

2.2.1 热力边界条件

由经典内弹道方程求解得到火药气体温度、压力及弹丸位移时变曲线如图2所示。由温度时变曲线可知，开始时刻对应火药燃烧爆温(2 800 K)，之后随弹丸动能的增加而逐渐下降，内弹道结束时温度降至1 900 K. 内弹道时期弹丸膛内运动位移时程曲线见图2，弹丸膛内行程长为7 680 mm，约12.6 ms对应弹丸出炮口时间。

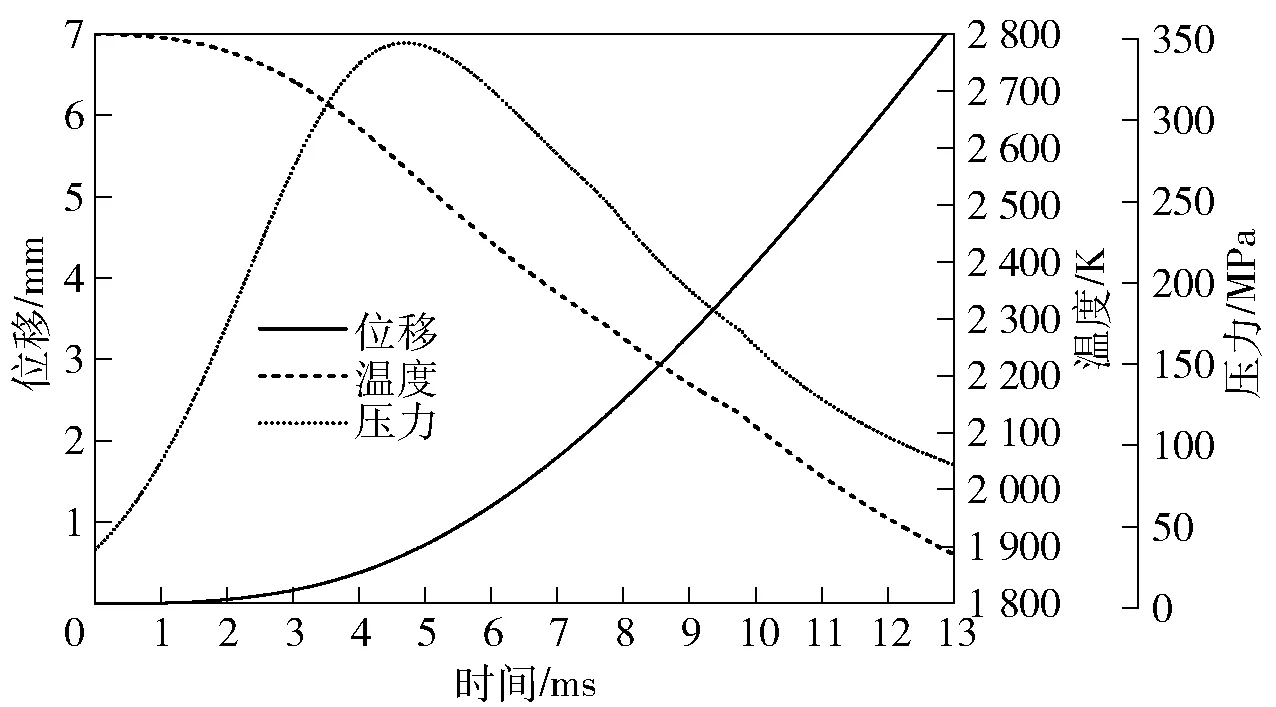
图2 动力学参量时程变化曲线Fig.2 Changing curves of dynamic parameters in the time domain

2.2.2 边界条件处理

计算得到的膛内平均压力曲线如图2所示，在4.8 ms时刻达到最大值348 MPa. 火药燃气在身管内为不稳定的湍流流动过程，通过强制对流换热过程，高温火药燃气穿过热边界层将热量传递给身管，该瞬态物理过程可以借助Abaqus软件中的接触边界film模块进行定义。弹丸运动位置控制热对流交换区域，并且热冲击载荷幅值随时间变化，用户可以根据自定义子程序(film子程序)实现该随动时变物理过程，基本思路为：

在每个载荷增量步，主程序调用子程序，同时主程序实时传递动力学系统物理参数至子程序，子程序被激活。用户在子程序体中自定义的功能模块针对每一个主程序选定的积分点做重复性命令，子程序在预知弹丸实时运动位置的前提下，对每一个积分点坐标进行监测，积分点坐标与弹丸位置对比，满足弹后位置条件下子程序对该积分点赋值为当前火药燃气温度，否则赋值为常温(295 K)[15]。子程序由主程序选定的积分点数量控制其计算次数，直至所有积分点完成赋值，该边界条件返回主程序等待下一个增量步。

身管内壁与火药气体之间的对流换热系数与二者温度差直接相关，内弹道时期动态的温度场变化历程使得热对流系数随之动态变化。在此将其定义为与温差相关的时变参量，同样由film子程序进行定义，在每个载荷增量步，程序体依据相应的物理规律并面向选定的所有积分点依次定义对应的热对流系数，由子程序自带的接口传入主程序。身管外壁与大气也主要考虑对流传热,大气温度设定为常温(295 K),对应的强制对流换热系数取值为常数26.57 W/(m2·K)。本文针对首发弹射击下的身管动力学响应进行分析，故身管整体初始温度设定为常温。

2.2.3 载荷边界条件

火药燃气密封于弹后空间，其压力效应作用于身管内壁，作用区域随弹丸膛内运动而动态变化。该载荷随动边界条件可以由载荷条件子程序实现，其实现方法与热对流温度边界定义方法类似，由子程序根据弹丸运动位置定义内壁受载区域。在每个载荷增量步，该方法面向主程序事先选定的积分点集合逐一定义其边界值，其实现流程示意图如图3所示。

图3 子程序实现载荷边界随动过程示意图Fig.3 Flow chart of subroutines for implementing the follow-up process of loading boundary

3 结果分析

为定性分析高温高压气体对身管性能的影响，建立局部空间柱坐标系(r,θ,z)，其中，坐标原点于身管尾端面中心，r轴为半径方向，θ轴为圆周方向，z轴沿身管轴线方向，指向炮口为正。

3.1 身管温度响应及热应力分析

高温气体被限制在膛底与弹底之间的膛内空间，即弹后身管内壁为形成强烈热对流交换的区域。通过数值仿真软件建立首发射击时虚拟热物理场变化过程，由数值模拟得到身管热分布以及对应的热应力分布云图。为清晰展示身管在可动边界条件下热场响应结果，取身管纵截面，并提取不同时刻温度分布图如图4所示。

图4 身管纵截面温度分布云纹图Fig.4 Temperature distribution in the longitudinal cross-section of barrel

图4直观再现了整个身管结构在首发射击时的温度演变过程，热对流边界区域随时间而动态变化，该区域由实时弹丸运动位置进行定义。高温气体与身管内壁之间通过强制热对流的方式传输热量，身管内壁率先升温，内部通过传热的方式进行能量传递。不同时刻对应不同的热对流区域，身管温度分布呈现不同的状态，靠近炮尾的身管部分率先接触高温气体，因此该部位的温度高于其他部位。随着时间的推移，对流热交换能量的累积使得身管各个部位均处于升温状态，身管温度轴向分布呈现越来越强的非均匀性，可以解释身管内壁烧蚀磨损的非均匀性。12.6 ms对应膛内运动结束时刻，身管温度达到最大值，此时药室内壁局部位置(85 mm，30°，21 mm)温度可达1 168 K(见图5)，明显高于靠近炮口部分。与文献[16]基于给定热冲击边界条件下进行身管某断面热传递过程分析时忽略了轴向温度梯度的影响不同，本文在其基础上，数值计算了可动边界条件下高温燃气与身管之间的热交换过程。实际火药气体与身管对流换热边界随时间而动态变化，轴向不同位置承受不同的瞬时热冲击载荷，对应的温度响应不同，任意时刻对应的身管温度响应存在明显的轴向温度梯度。

图5 12.6 ms时刻对应的身管温度分布图Fig.5 Temperature distribution at the time of 12.6 ms

为分析身管在三维空间内温度变化规律，沿轴向在身管内壁(r=85 mm)标记4个积分点，A点(z=620 mm)位于药室部，D点(z=6 505 mm)靠近炮口位置，B点(z=2 766 mm)、C点(z=5 006 mm)位于二者之间，图6记录了所选积分点在时域内的温度变化历程。

图6 轴向不同积分点温度变化曲线Fig.6 Changing curves of temperature at specific points

4个积分点对应不同的温升结果，A点位于药室部位，其温升先于其他积分点。身管内壁的温升过程是一个缓慢的物理演变过程，温升速率取决于对流热密度，热对流密度随着火药燃气与内壁温差的减小而逐渐减小，内壁温升速率趋于平缓。靠近炮口处身管内壁温升曲线具有一定延时，弹丸经过时开始对流热交换，温升曲线走势基本一致。轴向不同位置质点温升的延时性导致身管在轴向出现一定的温度梯度，势必带来一定的热应力。

火药气体对身管不同断面传递的热量一般取决于二者的温度差以及火药气体的作用时间，药室部承受整个内弹道时期热冲击作用，其温升较剧烈。选取A点所在药室部横截面为对象，得到不同时刻对应的温度分布图如图7所示，所选时刻与纵截面温度分析部分相同。

图7 药室部横截面温度分布图Fig.7 Temperature distribution in the cross-section of chamber

内弹道时期，药室内壁承受强烈的热冲击作用，计算结果显示，在给定的计算时间内，火药燃气温度一直高于身管温度，身管横截面一直处于升温状态。而在身管传导热阻的影响下，内弹道时期对应的极短时间内热量来不及向外传递，靠近内壁区域温度较高，并沿径向很快降至环境温度。由于热冲击载荷均匀分布假设以及结构对称简化，计算得到的横截面温度呈中心对称环状分布，从内到外温度值逐渐降低，沿径向存在一定的温度梯度。文献[17]在对无镀铬身管烧蚀的研究中发现，温度对身管内壁烧蚀的影响最大。由计算得到的温度分布可知，温度响应剧烈区域主要分布在距内壁Δr<15 mm范围内，其他区域温升不超过100 K，是造成炮膛内壁或涂层材料烧蚀破坏的直接根源。

图8记录了不同时刻A点所在药室部横截面不同径向位置对应的温度，结果显示径向温度分布存在较大差异，导致身管截面出现较大的温度梯度。随着身管不断升温，温度梯度逐渐增强，12.0 ms时，身管内壁(r=85 mm)温度达到1 160 K，并在距内壁18 mm(r=103 mm)处基本降至环境温度，该区域径向平均温度梯度为48.1 K/mm.

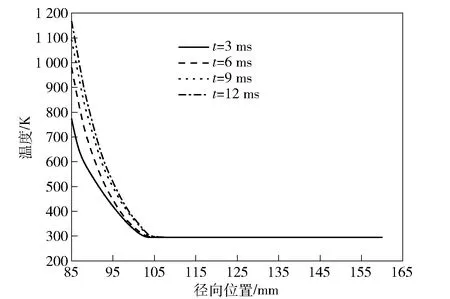
图8 不同时刻药室部径向温度分布Fig.8 Temperature distribution along radial direction

由计算得到的身管温度分布可知，不同时刻身管在三维空间内存在较明显的温度梯度，不同位置热膨胀的差异导致身管内部出现一定的温差应力。图9列出了不同时刻身管纵截面温差应力分布。由图9可见，不同时刻对应不同的应力状态，应力最大值均出现在药室部，其变化规律与温度分布变化规律相近。在内弹道结束时刻，轴向z=41 mm处身管内壁(r=85 mm)热应力最大值接近500 MPa，表明热冲击载荷在身管强度分析方面是不可忽视的因素。

图9 不同时刻身管温差应力分布图Fig.9 Thermal stress distribution at different times

选取与热分析部分相同的位置并提取其应力变化曲线，如图10所示。由图10可见，4个积分点对应的应力变化规律与温度变化规律相似，其应力值与温度梯度值直接相关。

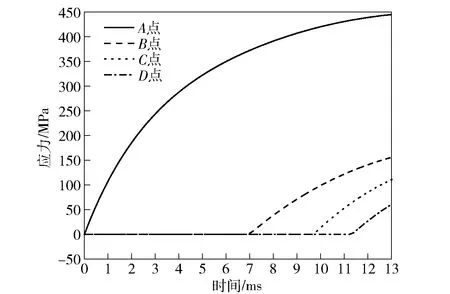
图10 轴向不同积分点温差应力时程曲线Fig.10 Thermal stress curves at specific points

选定A点对应的横截面，图11显示了首发弹射击时温差应力在该平面内的分布规律，对应时刻为12.6 ms，此时身管截面温度梯度达到最大值。应力呈环状分布，身管内壁表面温度梯度最明显，距内壁Δr<18 mm范围内，应力值高于360 MPa，身管内壁温差应力最大值接近447 MPa，并沿径向逐渐衰减。由得到的身管截面温度分布可知，首发射击时身管外壁的温度梯度可以忽略，但内壁质点体积膨胀产生的温差应力以应力波的形式传至外壁，使其应力值可以达到131 MPa.

图11 药室部横截面应力分布云纹图Fig.11 Stress distribution in the cross-section of chamber

身管局部质点热膨胀难以充分自由变形，沿径向受到身管壁厚的约束，沿周向以及轴向的变形受到相邻材料的约束。提取积分点A对应的应力分量变化曲线(见图12)，由计算结果可知，在热冲击载荷作用下，身管内壁主要表现为压应力，压应力对于抑制内膛裂纹扩展是有利的。随着药室部温度以及温度梯度的增加，各应力分量值均随之增加，在内弹道结束时刻达到最大值。由于内壁质点热膨胀沿径向较自由，只有一侧受到临近材料的约束，相比其余两个分量，径向应力分量变化幅值在数值上相差近一个数量级。另外，轴向应力分量数值高于周向应力，表明轴向温度梯度对身管热应力的影响不可忽视，现有的大部分文献在分析身管热应力时均将其简化为平面应变问题，对实际物理模型过度简化，计算结果与实际应力响应存在较大误差。

图12 热冲击作用下药室内壁应力分量时程曲线Fig.12 Stress component curves for chamber portion under thermal shock effect

3.2 气体压力激励下身管应力响应

气体压力作用于身管内壁的随动边界条件由子程序进行定义，得到的身管应力分布演变过程如图13所示，清晰地再现了气体压力作用效能。与热应力高响应区主要集中于身管内壁较薄区域不同，压力作用下身管横截面应力呈均匀渐变分布，且拥有较大幅值。不同时刻对应不同的压力值以及作用边界，其应力计算结果随之变化，临近压力最大值时刻的身管应力值高于其他时刻。由选定时刻对应的身管应力分布结果可知，前2个时刻对应的应力最大值位于药室部，后4个时刻对应的身管应力最大值位于载荷作用区域前端。

图13 压力作用下身管应力分布演变过程Fig.13 Barrel stress evolution process under gas pressure

身管不同截面对应不同的结构特征以及压力作用过程，图14显示了4个选定位置等效应力变化曲线。由图14可见，A点应力变化规律与气体压力相近，B、C、D3点应力曲线呈现明显的阶跃性，与相应的载荷作用突变特性相关，符合实际物理场变化规律。

图14 压力作用下单点应力时程曲线Fig.14 Stress curves at specific points under gas pressure

图15显示了A点对应的应力分量变化过程，与温差应力相比，压力作用下应力分量值由载荷值决定。由于身管近似为变截面厚壁圆筒结构，压力作用下质点不会出现轴向变形，故轴向应力分量值较小。由拉梅公式可知，身管内壁质点在径向表现为压应力，周向为拉应力，其数值变化曲线与压力曲线一致。

图15 药室部积分点应力分量变化曲线Fig.15 Stress component curves for chamber portion under gas pressure

3.3 热力联合作用下身管应力响应

基于可动边界条件建立的热力联合作用数值模型计算得到的身管应力分布图如图16所示。由图16可见，相比图13所示的应力结果，应力响应区前端所受载荷主要为气体压力冲击载荷，此时温差应力可忽略不计，对应的应力值基本一致。药室部温度响应剧烈，应力结果由热冲击载荷以及压力冲击载荷共同主导，应力演变过程明显不同，5.0 ms与7.0 ms时刻对应的药室部应力值明显小于图13对应的应力结果，而11.0 ms与12.6 ms时刻对应的应力值则大于图13对应的应力结果。与图13所示大约5.3 ms时刻之前身管应力最大值位于药室部不同，热力联合作用下应力最大值点在大约2.6 ms时刻后转移至应力区前端。

图16 热力联合作用下身管应力演变过程Fig.16 Barrel stress evolution process under the joint effect

身管内壁4个积分点的应力变化曲线如图17所示，A点位于药室部，考虑温度效应得到的应力变化规律与图14所示的结果不同，应力幅值明显变小。图14中A点等效应力与压力变化规律一致，最大值为692.8 MPa，在内弹道结束时刻随之降至182.1 MPa. 而热力联合作用下对应的最大值为520.6 MPa，应力曲线在9.8 ms以后呈现逐渐上升的趋势，并在12.6 ms时刻增至332.6 MPa.B、C、D3点对应的结果与A点基本一致，应力峰值出现在载荷开始作用时刻，此时压力激励占据主导位置，随着温差应力的逐渐增大，其应力幅值同样随之减小。由此可知，温度梯度产生的温差应力可在一定程度上改善身管的整体应力分布。

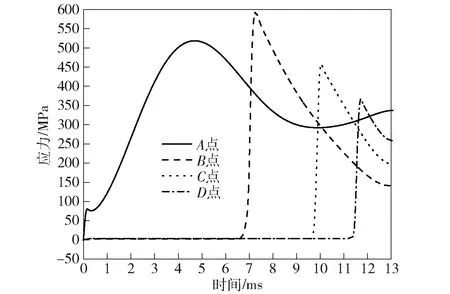
图17 热力联合作用下单点应力时程曲线Fig.17 Stress curves at specific points under the joint effect

为分析单点等效应力变化规律，提取A点应力分量如图18所示。径向压力激励下(见图15)，A点周向应力最大值可达到508 MPa，表现为拉应力。而温差应力周向分量则表现为压应力，鉴于单向应力的叠加关系，热力联合作用使得周向应力值减小，最大值降为208 MPa，并在7.5 ms时刻逐渐变为0 MPa，之后演变为数值递增的压应力，热力联合作用下得到的身管内壁周向拉应力以及压应力的交互作用与身管内表面疲劳微裂纹的产生直接相关。压力激励得到的A点轴向应力接近0 MPa，因此热力联合作用下得到的轴向应力结果与温差应力轴向分量基本一致。热冲击以及压力激励得到的A点应力径向分量均表现为压应力，压力激励下得到的应力径向分量最大值为258 MPa，相应的热力联合作用下得到的最大值为305 MPa.

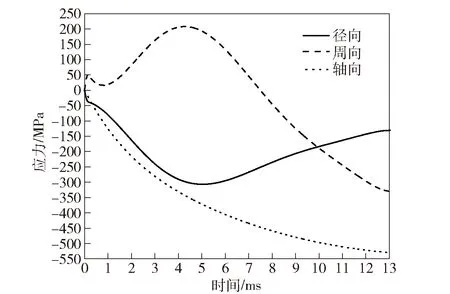
图18 热力联合作用下药室部应力分量曲线Fig.18 Stress component curves for chamber portion

等效应力是衡量身管工作可靠性的有效物理参量，依据von Mises屈服准则，图19为压力激励作用以及热力联合作用下不同时刻对应的身管等效应力最大值。由图19可见，计算结果曲线呈一定的抛物线型，幅值随载荷以及承载区域而动态变化。

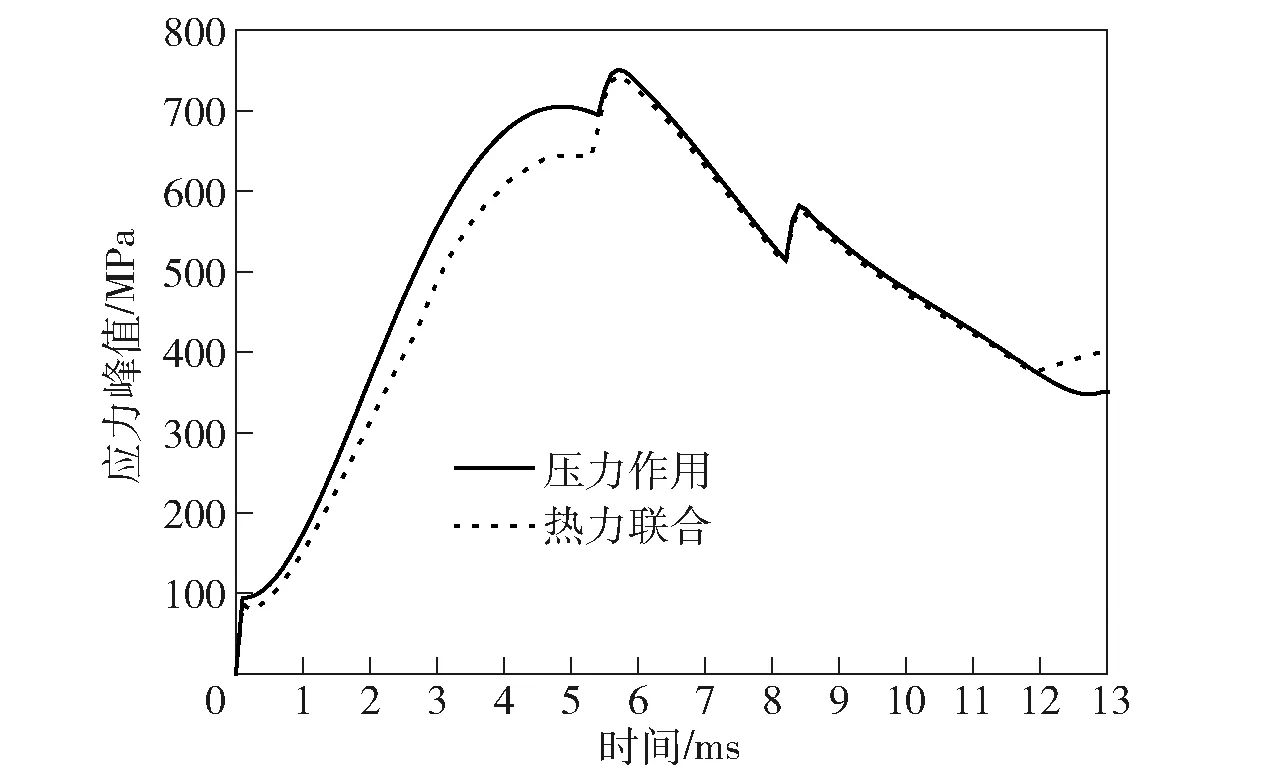
图19 应力峰值时程曲线Fig.19 Time history of maximum stress in barrel

压力激励作用下，5.3 ms时刻之前应力最大值曲线与图14中A点应力变化曲线基本一致，表明该时刻之前最大应力位于药室部，之后前移至直膛段。身管应力最大值曲线存在两个极大值点，分别对应身管结构突变位置。

热力联合作用下，5.3 ms时刻前应力峰值曲线的幅值明显小于同时段压力激励下得到的结果，并且该时段应力结果与A点应力变化过程并不一致，表明应力最大值并不完全位于药室段。温度膨胀导致身管内壁周向应力表现为拉应力，与压力作用对应的拉应力进行叠加，在一定程度上减小了周向应力数值，从而有效减弱了身管应力水平，当然这并不能表明身管处于更安全的状态，身管材料随着温度的升高表现为热软化特性，其屈服极限会随之下降，因此内膛的安全系数可能会随之降低。

纵观整个内弹道过程，5.3 ms时刻后，热力联合作用与压力作用得到的身管应力峰值以及对应的位置较一致，该时段身管动强度主要由压力激励控制。身管应力最大值(752 MPa)出现在约5.6 ms时刻，位于身管直膛段，此时该位置热效应可以忽略。

4 结论

本文通过有限元软件提供的子程序接口定义了火药燃气作用边界随弹丸运动而变化的动态过程，进而分析了首发弹射击条件下身管温度演变规律，并分析了气体热力效应对身管强度的影响。所得结论如下：

1) 身管轴向不同位置热冲击时差性带来一定的轴向温度梯度，并且温度响应剧烈区域主要分布在距内壁Δr<15 mm范围内，该区域径向温度梯度平均值可达48.1 K/mm.

2) 身管内部温度分布非均匀性造成的温差等效应力最大值接近500 MPa，表明火药燃气热效应在身管强度分析方面是不可忽视的因素。

3) 热力联合效应下，周向表现为压应力的温差应力与表现为拉应力的载荷应力相互叠加，使得内壁应力周向分量表现为拉应力与压应力的交互作用，高温响应区应力幅值得到一定减弱，并随温度响应呈现先下降后上升的趋势，分析结果可以为身管动强度设计理论提供一定的参考依据。