基于HyperFLOW平台的客机标模CHN-T1气动性能预测及可信度研究

王年华, 常兴华, 赵 钟, 马 戎, 张来平

(1. 中国空气动力研究与发展中心 空气动力学国家重点实验室, 绵阳 621000；2. 中国空气动力研究与发展中心 计算空气动力研究所, 绵阳 621000)

0 引 言

近年来，针对实际飞行器外形的CFD气动性能预测及可信度研究逐步得到重视。美国AIAA自2001年至2016年，共举办了6届阻力预测研讨会(Drag Prediction Workshop, DPW)[1-2]，主要针对DLR-F4、DLR-F6、NASA Common Research Model (CRM)等运输机客机标模研究CFD数值模拟方法、数学物理模型、不同求解器对实际外形的气动特性预测精度，通过不同结果之间的比较分析，评估当前CFD技术模拟运输机高速构型阻力预测的能力[3]，探索提高CFD预测精度的可能途径。类似的活动还有AIAA发起的高升力预测研讨会(High Lift Prediction Workshop, HiLift-PW)[4-5]，其目的和手段均与DPW类似，只是研究对象存在差异。

为评估CFD当前技术状态，促进国内CFD验证与确认工作及可信度研究的发展，中国空气动力研究与发展中心联合国内五家单位共同组织了第一届航空CFD可信度研讨会(AeCW-1)，主要针对中国空气动力研究与发展中心自主设计的CHN-T1客机标模的3种构型，设计了定升力系数网格收敛性研究和抖振特性研究等2个必选算例，以及雷诺数影响研究等1个可选算例。

本文基于作者所在课题组研发的HyperFLOW求解器，对客机标模CHN-T1[6]进行了气动性能预测及可信度研究。首先，采用NASA Turbulence Modeling Resources[7-9]中的NACA0012翼型低速湍流流动算例进行网格收敛性研究，验证了求解器对简单湍流问题的模拟能力和网格收敛性。其次，按照AeCW-1官方要求的必选算例，采用研讨会官方提供的非结构网格[10]，考察了复杂外形数值模拟的网格收敛性和气动特性的预测精度；同时也研究了模型尾撑、静气动弹性变形、湍流模型等对气动特性预测精度的影响。

1 数值方法与计算平台简介

本文所采用的流动控制方程为积分形式的控制方程：

式中:W为守恒变量，Fc为无黏通量矢量，Fv为黏性通量矢量。

方程采用格心型非结构二阶精度有限体积法进行离散。根据DPW的经验[2-3]，对于CRM标模，采用Quadratic Constitutive Relation(QCR)关系式对基于线性涡黏性模型的SA模型进行修正，可以更为准确地模拟翼身结合部的分离泡，从而得到更为精确的气动力和力矩，因此本文在模拟湍流流动时，除选用原始SA一方程湍流模型外，同时比较了SA-QCR2000模型[11-12]对流动模拟精度的影响。QCR关系式如下：

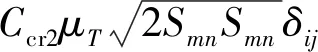
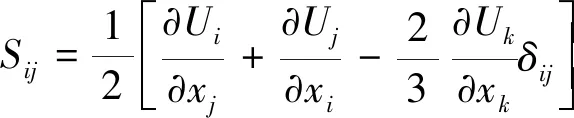
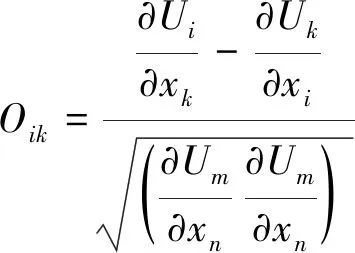
本文所采用的计算平台为作者团队自主开发的结构非结构混合解算器HyperFLOW[13-14]。该解算器的空间离散采用了二阶精度的格心型有限体积方法。集成了Roe、vanLeer、AUSM、Steger-Warming等通量计算格式以及Barth、Venkatakrishnan等多种限制器函数。湍流模拟方法有SA一方程湍流模型、SST两方程湍流模型以及DES方法等。时间离散格式有Runge-Kutta、隐式BLU-SGS等方法。为了适应大规模工程计算的需求，两种解算器均发展了基于网格分区的大规模并行计算技术。关于该软件的设计思想和研究进展，请参见文献[13,14]。其相对成熟的公开版本——“风雷(PHengLEI)”[15-16]已经在业内免费发布。

针对本文的标模算例，无黏通量采用Roe格式，梯度重构为节点型的高斯格林法GG-Node方法，由于本文所计算的算例属于亚跨声速，即便有激波出现，其强度也较弱，因此我们采用的迎风格式隐含合适的数值耗散能有效抑制激波处的非物理波动，所以本文所有算例均未采用限制器，黏性通量格式为法向导数法[17]，时间推进采用LU-SGS隐式格式，湍流模型考察一方程原始SA模型及引入QCR修正的SA-QCR2000模型[12-13]，CFL数在0～2000步内从1增大到10，采用128核并行计算。

2 湍流模型验证

为了更加严谨的对湍流模型及其实现过程进行验证与确认，DPW V和DPW VI组委会选择了NASA Turbulence Modeling Resources(TMR)[7-9]中的二维湍流平板、二维Bump、二维NACA0012翼型绕流等几个简单湍流算例进行网格收敛性研究，考核各种解算器湍流模拟的能力及模型实现过程的差异。其中在DPW VI中，二维NACA0012的网格收敛性研究成为必选算例之一[1]。在第2届High-Lift Prediction Workshop中，也选用了二维Bump算例作为可选算例对湍流模型进行验证[5]。

本节采用TMR中的二维NACA0012算例对湍流模拟进行网格收敛性研究，考核本文所采用的求解器对简单湍流问题的模拟能力和网格收敛性。

二维NACA0012翼型低速绕流计算条件为：Ma=0.15，Rec=6×106，c=1，AOA=10°，Tref=300 K，直接采用TMR提供的7套依次稀疏化的如图1所示的C型Family II结构网格(将其转换为非结构网格数据结构进行计算)，网格在尾缘处较密(Δs=1.25×10-5c)，对于尾缘流动旋涡、分离、剪切层的模拟会更加准确，网格远场距离物面大约为500c，最密的网格量为7169×2049，翼型表面布置4097个节点，物面法向第一层网格高度为1×10-7，y+≈0.03，法向增长率为1.02，最稀疏的网格量为113×33，物面布置65个节点，更多信息可参考TMR[9]。

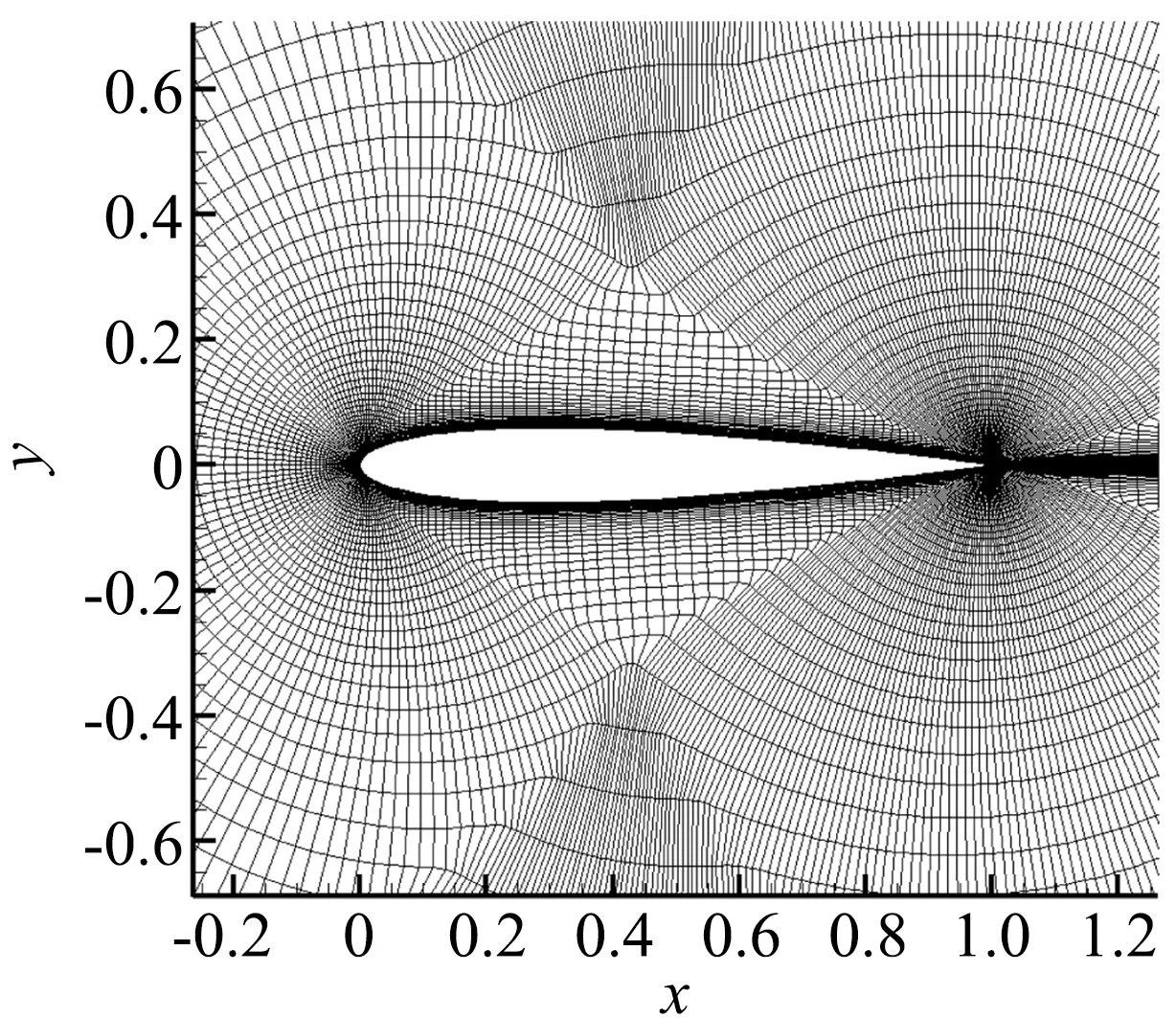
图1 2D NACA0012算例网格示意图Fig.1 Grid of the 2D NACA0012 case

图2给出了各向异性矩形网格上的网格收敛性测试结果，同时还给出了CFL3D、FUN3D和TAU采用SA湍流模型的计算结果[9]。本算例的湍流模型也为SA模型。结果显示：在最密网格上，气动力系数和力矩系数与其他求解器相仿，显示本文采用的湍流模型具有较好的可信度。

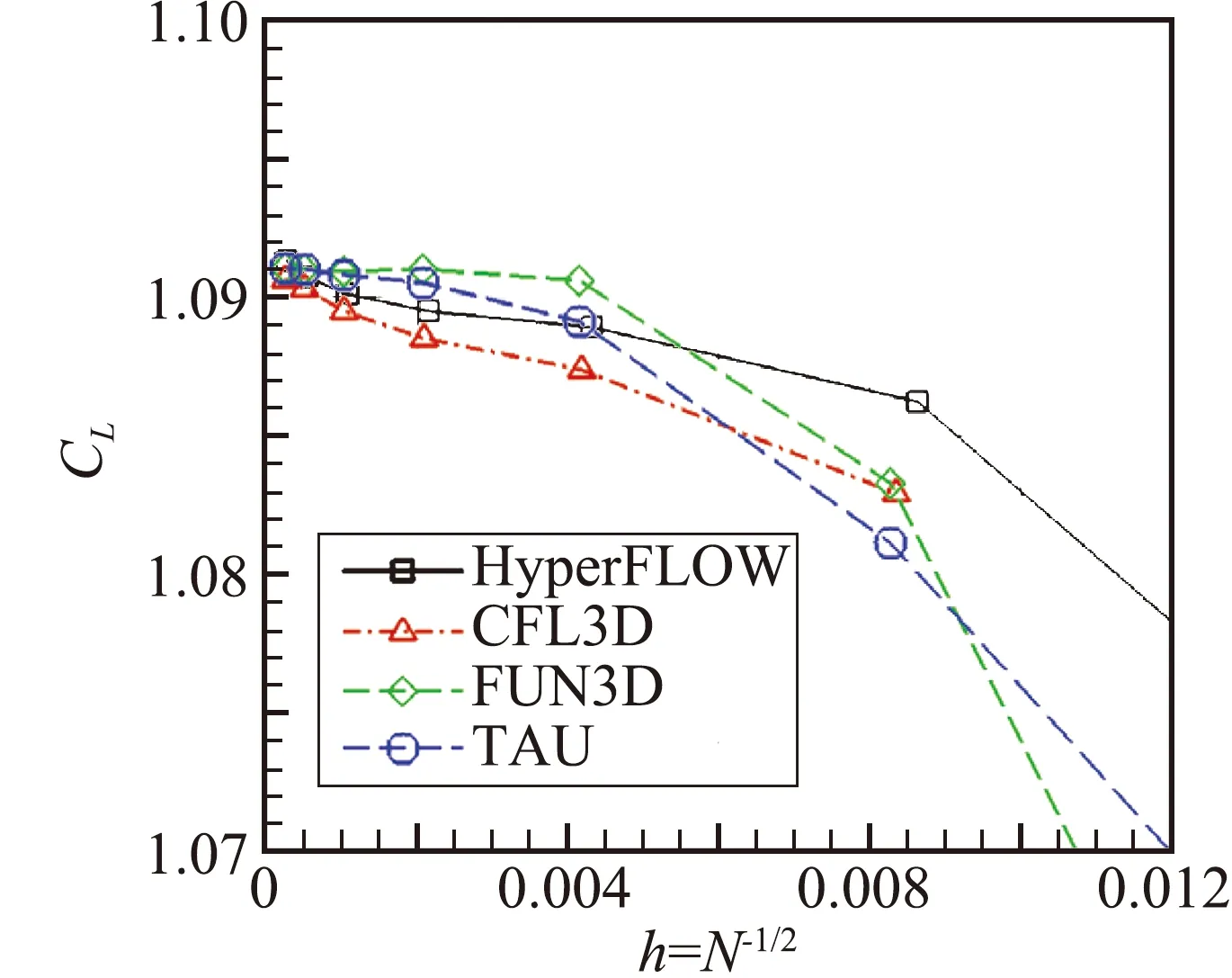
(a) Lift coefficient

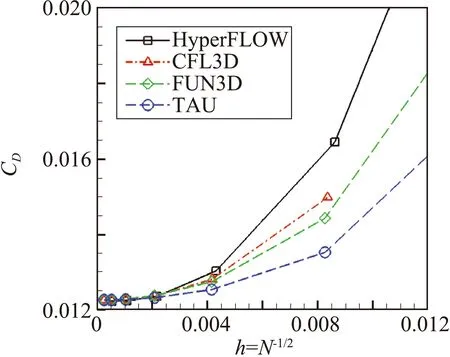
(b) Drag coefficient

(c) Moment coefficient

3 CHN-T1标模算例及网格

CHN-T1标模是中国空气动力研究与发展中心设计的典型高亚声速单通道客机标模。第一届航空CFD可信度研讨会(AeCW-1)选择该标模的3种构型作为CFD可信度确认的模型，关于该标模的气动外形设计可以参考文献[6]。

研讨会主要考虑3种构型：1) Config.1：Wing/Body/Tail，即翼身组合体+尾翼构型；2) Config.2：Wing/Body/Tail + Support，即在构型1的基础上增加尾撑；3) Config.3：Wing/Body/Tail + Support + static elastic deformation，即在构型2的基础上考虑静气动弹性变形。

在算例设置方面，AeCW-1主要包括2个必选算例和1个可选算例。本文主要选择其中2个必选算例，算例条件如下：

Case1(必选算例)：定升力系数网格收敛性研究，基于Config.1采用官方提供的基础网格或自行生成的网格，进行定升力系数的网格收敛性研究。计算状态为Ma=0.78，CL=0.5(±0.001)，Rec=3.3×106，T=300 K。

Case2(必选算例)：抖振特性研究，分别基于3种构型的中等网格(分别记为case2a，case2b和case2c)，进行气动力和力矩的预测。计算状态为：Ma=0.78，Rec=3.3×106，T=300 K。计算迎角取α=-2.0°，-1.0°，0°，1.0°，2.0°，3.0°，3.5°，3.75°，4.0°，4.25°，4.5°共计11个迎角状态。

本文采用的计算网格为研讨会官方提供的非结构网格[10]。Config.1包含粗、中、密3套网格，Config.2只有1套中等网格，而由于不同迎角变形不同，Config.3则共有11套中等网格(由作者根据Config.2的初始非结构网格生成静气动弹性变形后的网格，提供研讨会官方使用)，其网格量如表1所示。Config.3中等网格的网格量和Config.2中等网格基本相同，在此不再列出。

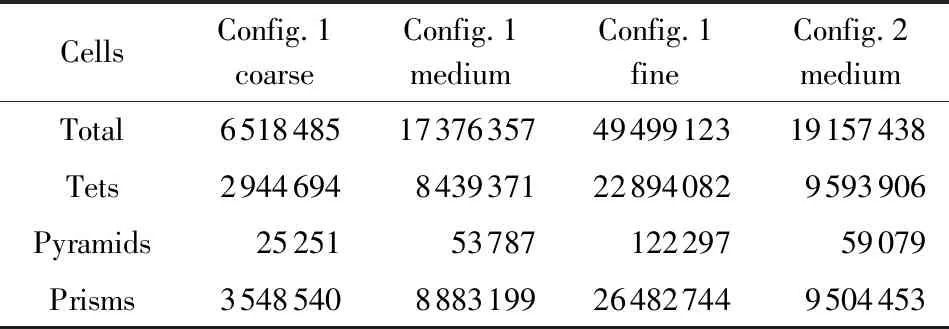
表1 CHN-T1标模非结构网格信息Table 1 Grid information of CHN-T1 model

物面采用三角形单元离散，空间采用四面体、三棱柱、金字塔混合单元离散。图3给出了Config.1和Config.2的物面和对称面网格。

4 数值计算结果与分析

4.1 定升力系数网格收敛性

定升力系数网格收敛性研究的目的在于验证：(1) 数值模拟所采用的网格具有较好的网格质量；(2) 所采用的求解器和求解模型具有良好的网格收敛性和可信度，即为后续进行case2的抖振特性研究确定网格和数值离散格式。

图4给出了case1的定升力系数CL=0.5(±0.001)时迎角、总阻力系数、理想阻力和力矩的网格收敛性曲线。结果显示，在网格加密时，HyperFLOW的计算结果随着网格尺度N-2/3的收敛过程接近线性，说明数值结果是近似2阶收敛的，具有较好的网格收敛性。

(a) Config.1

(b) Config.2

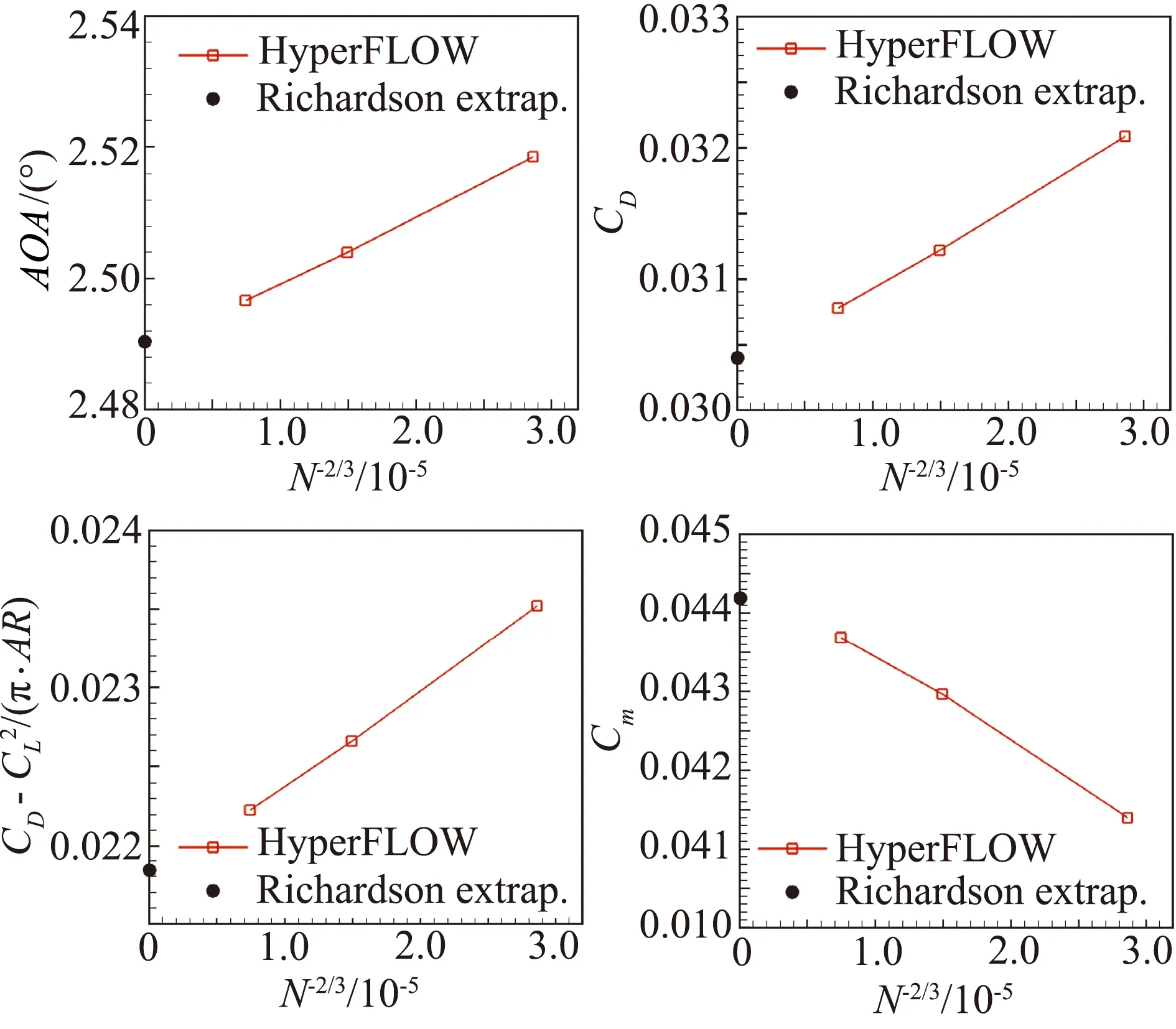
图4 case1定升力系数网格收敛性Fig.4 Grid convergence tests results of case1

表2给出了定升力系数网格收敛性研究中粗、中、密3套网格计算得到的升力系数、迎角、总阻力系数、摩阻系数和力矩系数计算值、Richardson外插值(表中标注为Extrap.)、TRIP软件采用104亿结构网格计算得到的结果[18](标注为Trip)以及实验值Exp.(根据试验数据插值得到)以便读者参考。由表中数据可见，Richardson外插结果跟104亿结构网格的计算结果比较接近，其中迎角差异在0.15°以内，阻力系数差异为4.8 counts，摩阻系数差异为0.1 counts，力矩系数差异为3×10-4。

表2 网格收敛性研究计算值与实验值Table 2 Numerical results of grid convergence study and experimental data

在此要说明的是，定升力系数网格收敛性研究采用的模型为无尾撑的刚性模型Config.1，而试验模型则是带尾撑的弹性模型Config.3，因此实验值和数值结果会存在一些差异，可比性不高，比如表2中力矩系数数值结果和试验结果的偏差就比较大，此处给出实验值仅仅作为参考，并不与计算值进行比较。

除定性研究网格收敛性之外，在三套网格上计算数值结果的观测精度阶(observed order of accuracy,p)和网格收敛性指数(Grid Convergence Index,GCI)[19-20]，利用观测精度阶和网格收敛性指数的对数值结果的网格收敛性进行定量评估。

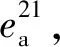
表3结果显示，迎角、总阻力系数、力矩系数的观测精度阶均能达到设计的二阶精度。此外，密网格数值结果和外插结果的阻力系数和力矩系数相对误差、GCI相对不确定度均在1.5%左右，显示出数值结果较小的不确定度。迎角的相对误差和GCI则小于0.5%，远小于阻力和力矩的不确定度，相对来说，阻力和力矩的不确定度及预测难度均要高于迎角。

表3 CHN-T1算例观测精度阶和GCITable 3 Observed order and GCI of CHN-T1 case1

4.2 模型尾撑及弹性变形的影响

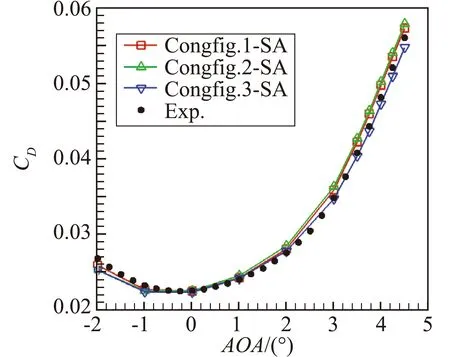
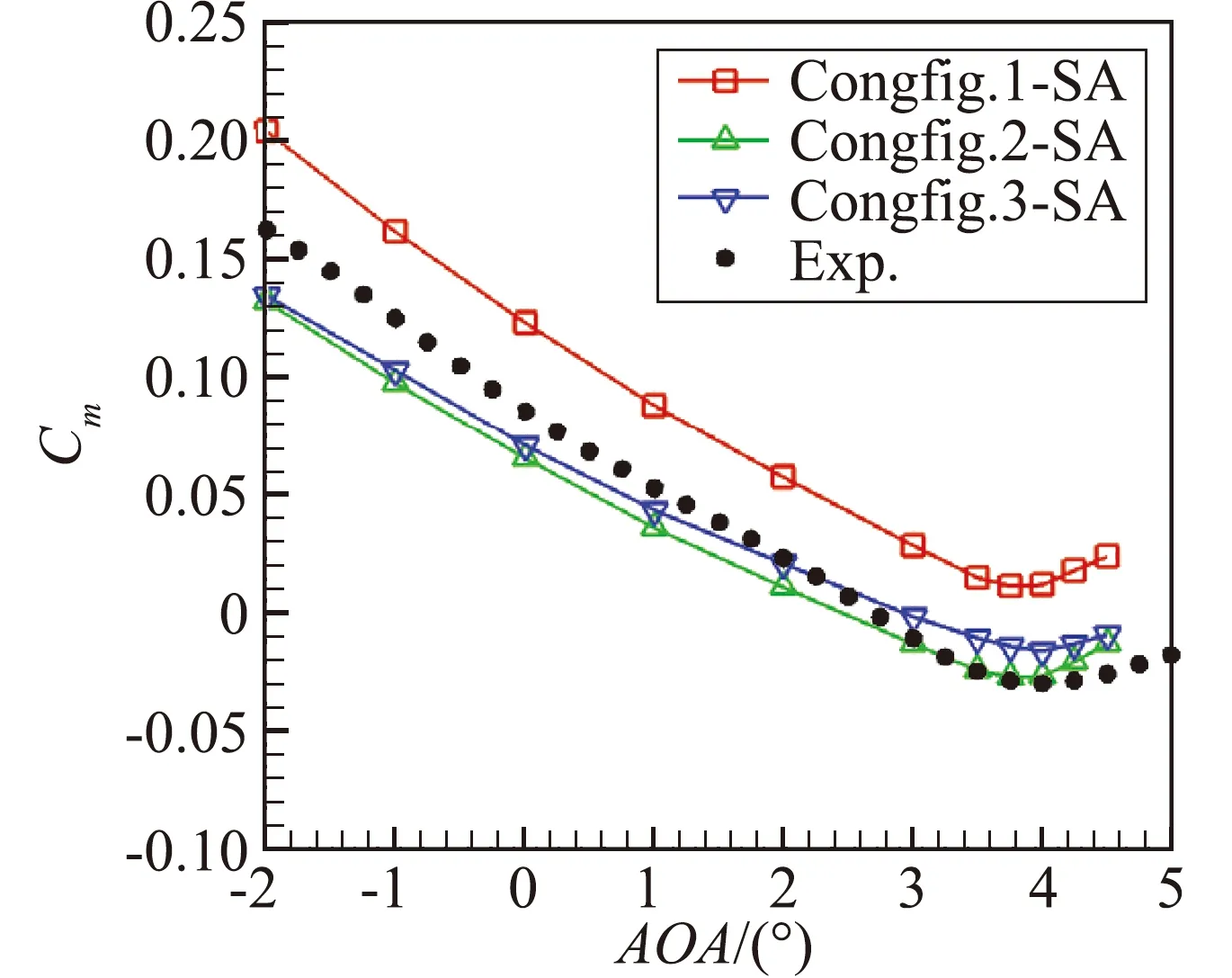
图5给出了Case2的三种构型中等网格的计算结果，并与实验值[21]进行了比较。结果显示，无尾撑构型(Config.1)的升力和阻力稍偏大，各个迎角力矩均为抬头力矩，且偏离实验值(Exp.)较远；当考虑模型尾撑(Config.2)时，升阻力仍然偏大，但是力矩明显比无尾撑构型更接近实验值，且在大迎角(大于2.75°)时力矩为低头力矩，说明尾撑对力矩的影响较大；在此基础上引入模型的静气动弹性变形(Config.3)，此时升阻力均与实验参考值吻合良好，力矩与Config.2相比存在细微差异，且在小迎角时更接近实验值，说明气动弹性对气动力和力矩的影响也不可忽略。文献[22]在CRM标模的气动数值模拟中也得到了类似的结论。

图6依次给出了AOA=3°时机翼η=0.17, 0.28, 0.41, 0.50, 0.65, 0.70, 0.85, 0.95, 0.98等9个站位和平尾η=0.28, 0.50, 0.95等3个站位的壁面压力分布。站位分布如图7所示。

由机翼各个站位的压力分布可见，Config.1与Config.2的差异极小，也即有无尾撑对机翼压力分布的影响极小；而Config.2和Config.3的差异十分明显，也即机翼的气动弹性变形对机翼压力分布有明显影响。

(a) Lift coefficient

(b) Drag coefficient

(c) Moment coefficient

图5 三种构型中等网格的气动力计算结果对比
Fig.5 Comparison of aerodynamic forces and moments of three configurations on medium grids

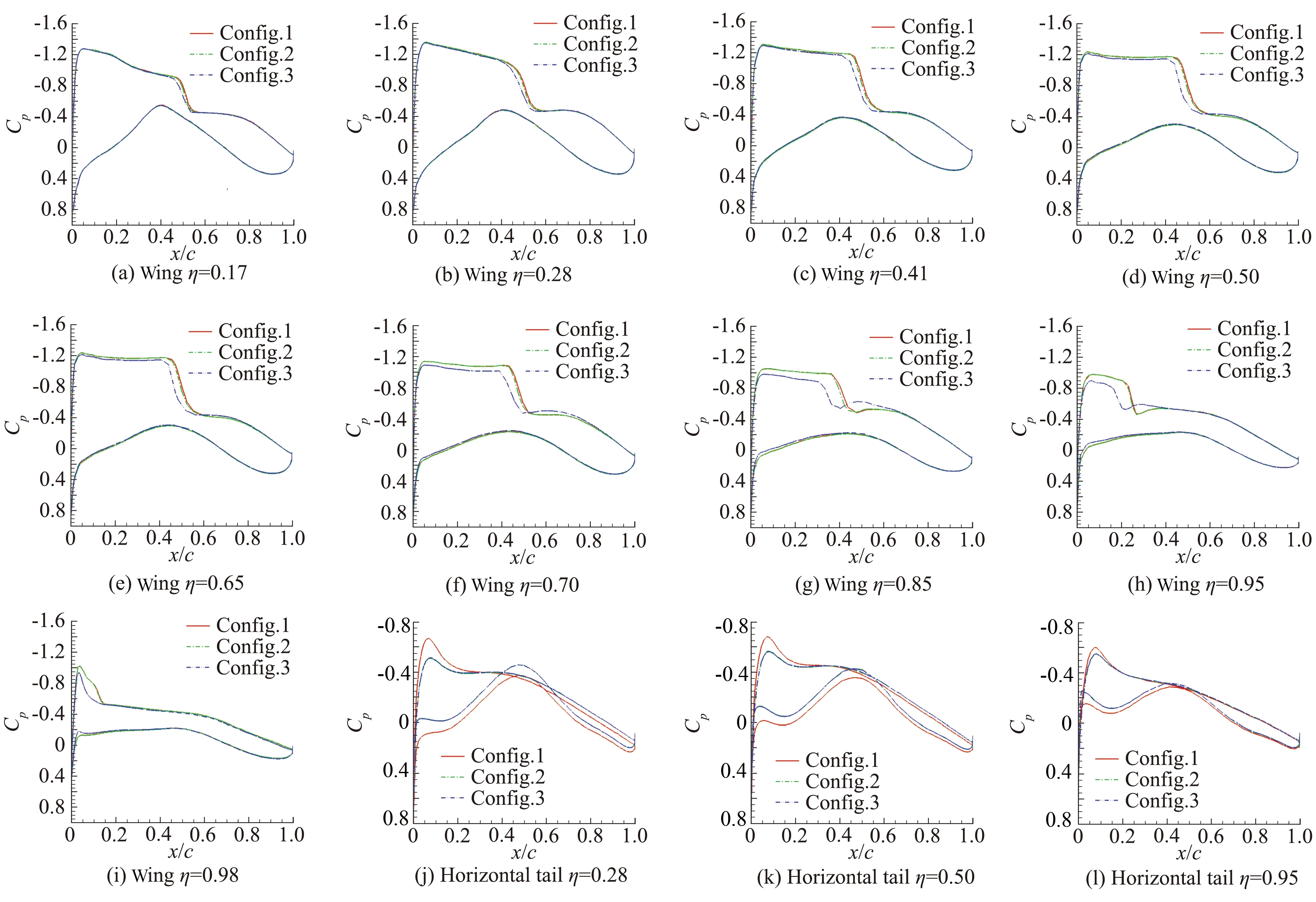
图6 三种构型机翼及平尾压力系数分布曲线Fig.6 Comparison of Cp distributions of wing and horizontal tail of three configurations

图7 机翼及平尾站位分布Fig.7 Stations on wing and horizontal tail wing

由平尾各个站位的压力分布可见，Config.2与Config.3的差异极小，即机翼弹性变形对平尾压力分布影响较小；而Config.1和Config.2的差异十分明显，也即尾撑对平尾压力分布影响显著，而且可以看到，Config.2平尾的压力分布曲线包络面积更小，也即平尾气动力更小，通常平尾提供负升力，也即Config.2会产生更小的负升力，因而导致了更小的抬头力矩和略微增大的整机升力系数(如图5(a)所示)。

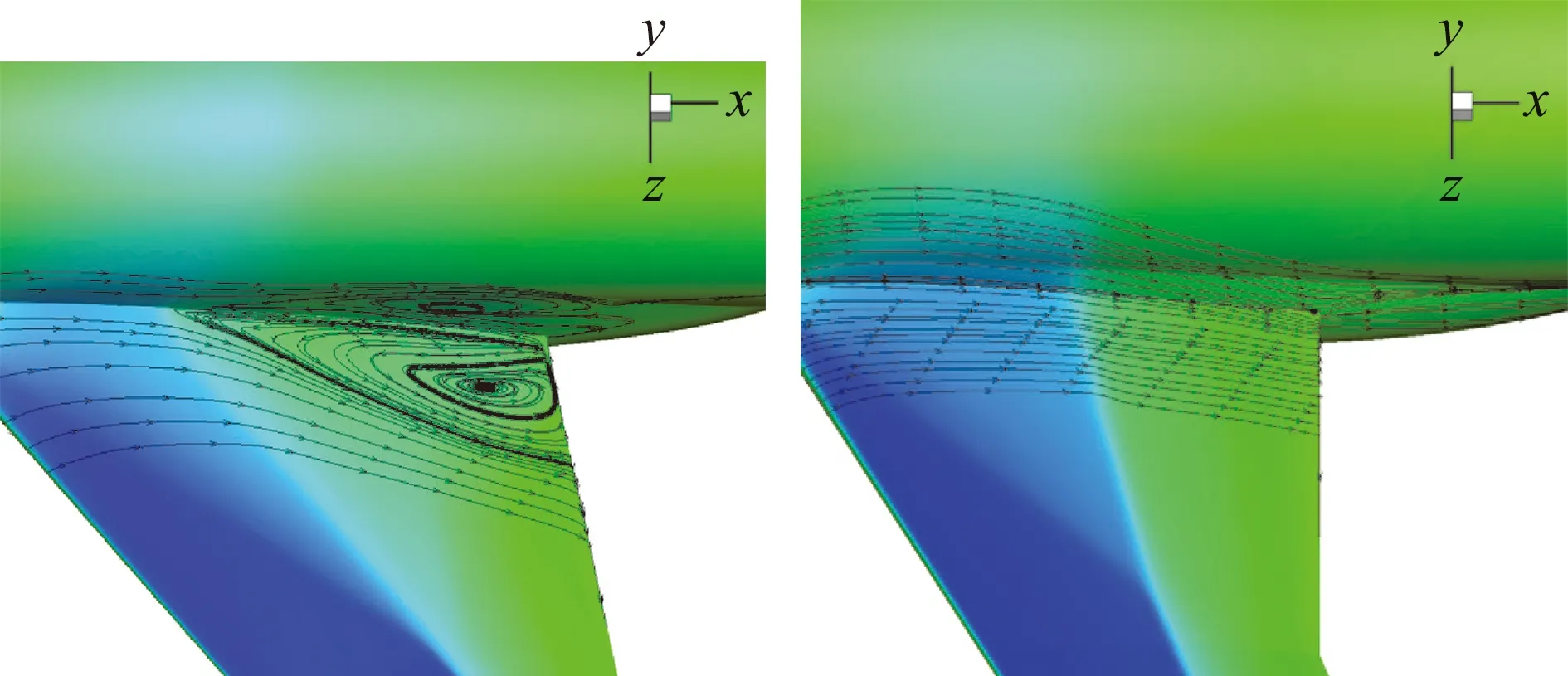
图8给出了机身后段和平尾附近的空间流线，由图可以看到Config.2在机身尾部存在顺时针流动分离涡，而Config.1并不存在这样的分离涡，由于分离涡的存在，导致离分离涡较近的平尾后缘流速加快，上下表面压力均减小；而对于离分离涡较远的平尾前缘，由于尾撑的阻塞作用，导致上翼面流速反而降低，因而压力系数增大，而前缘下翼面由于分离涡的诱导作用仍然较强，导致压力系数仍然呈减小趋势，这才形成了如图6(j)～图6(l)所示的压力分布曲线的趋势，整体来看，平尾气动力减小，这也解释了引入尾撑后，抬头力矩减小的原因。

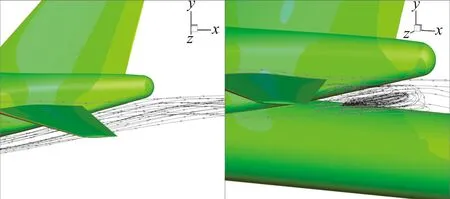
图8 AOA=3°尾部空间流线:Config.1(左), Config.2(右)Fig.8 Streamlines at AOA=3°, Config.1 (left), Config.2 (right)

综合来看，尾撑主要影响平尾的压力分布，而机翼静气动弹性变形主要影响机翼的压力分布，这两部分共同影响标模CFD气动预测精度。其中尾撑对平尾压力分布影响显著，这也体现到了气动力矩的预测精度上，考虑尾撑后，力矩预测精度显著提高；而机翼弹性变形对机翼压力分布也有明显影响，但是体现在积分的气动力上和力矩上并不显著。这主要是由于机翼梢部变形大，对压力分布的影响大，但是梢部面积小，因此在气动力积分中占据次要作用；其次，由于机翼与力矩参考点距离较近，因此气动力变化对力矩的影响也不显著。因此才形成了图5所示的气动特性变化规律。

4.3 湍流模型的影响

根据DPW V和DPW VI的经验[1-2]，在对NASA CRM标模进行数值模拟时，由于SA模型无法准确模拟翼身结合部的分离泡，导致在大迎角时(3°以上)，气动预测精度严重下降。采用Quadratic Constitutive Relation(QCR)对基于线性涡黏性模型的SA模型进行修正，可以得到准确的流动分离和气动预测结果。

由于CHN-T1标模算例与CRM标模算例一定程度上相似，但又存在一定差异，QCR修正对计算结果到底有何影响仍然有待研究，因此有必要在CHN-T1标模算例中考核SA模型和SA-QCR模型对流动模拟精度的影响。

图9给出了Case2b和Case2c分别采用SA模型和SA-QCR模型的气动力/力矩结果的对比。由图中曲线可以看到，SA模型和SA-QCR模型得到的升阻力系数比较接近，均与实验值吻合较好；但是力矩存在明显差别，主要体现在小迎角时SA-QCR模型计算得到力矩结果更加接近实验值，而在大迎角时SA模型的结果更接近实验值。

分析存在差异的原因，是由于SA-QCR模型计算得到的压力分布与SA模型存在一定差异。如图10所示，分别给出了采用SA模型和SA-QCR模型时，Config.3构型机翼(9个截面，分为3组)及平尾截面(3个截面)压力分布曲线。由图可见，两种湍流模型的压力分布在机翼激波位置附近，在平尾上均存在一定差异，导致两种模型计算得到的力矩存在差别。

(a) Lift coefficient

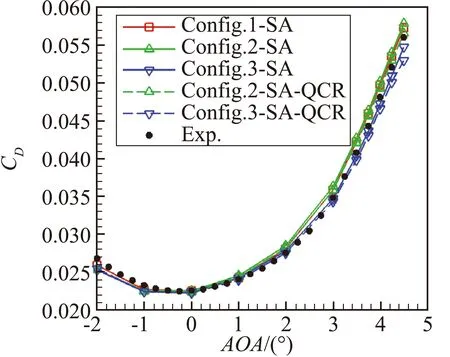
(b) Drag coefficient

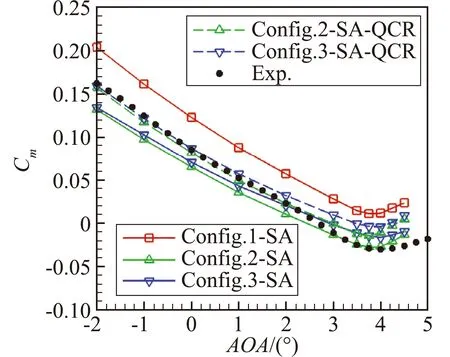
(c) Moment coefficient

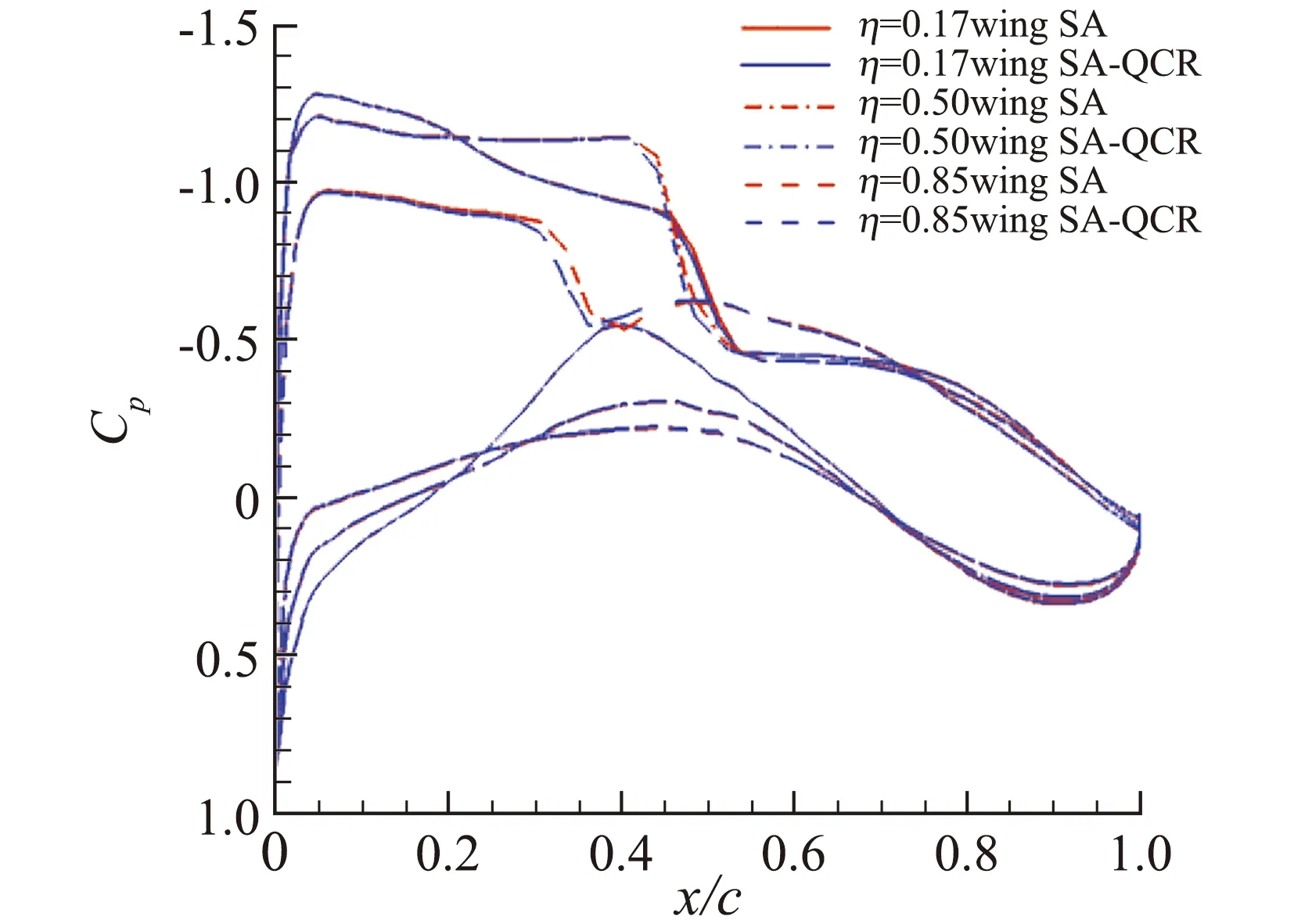
(a) Wing section group 1

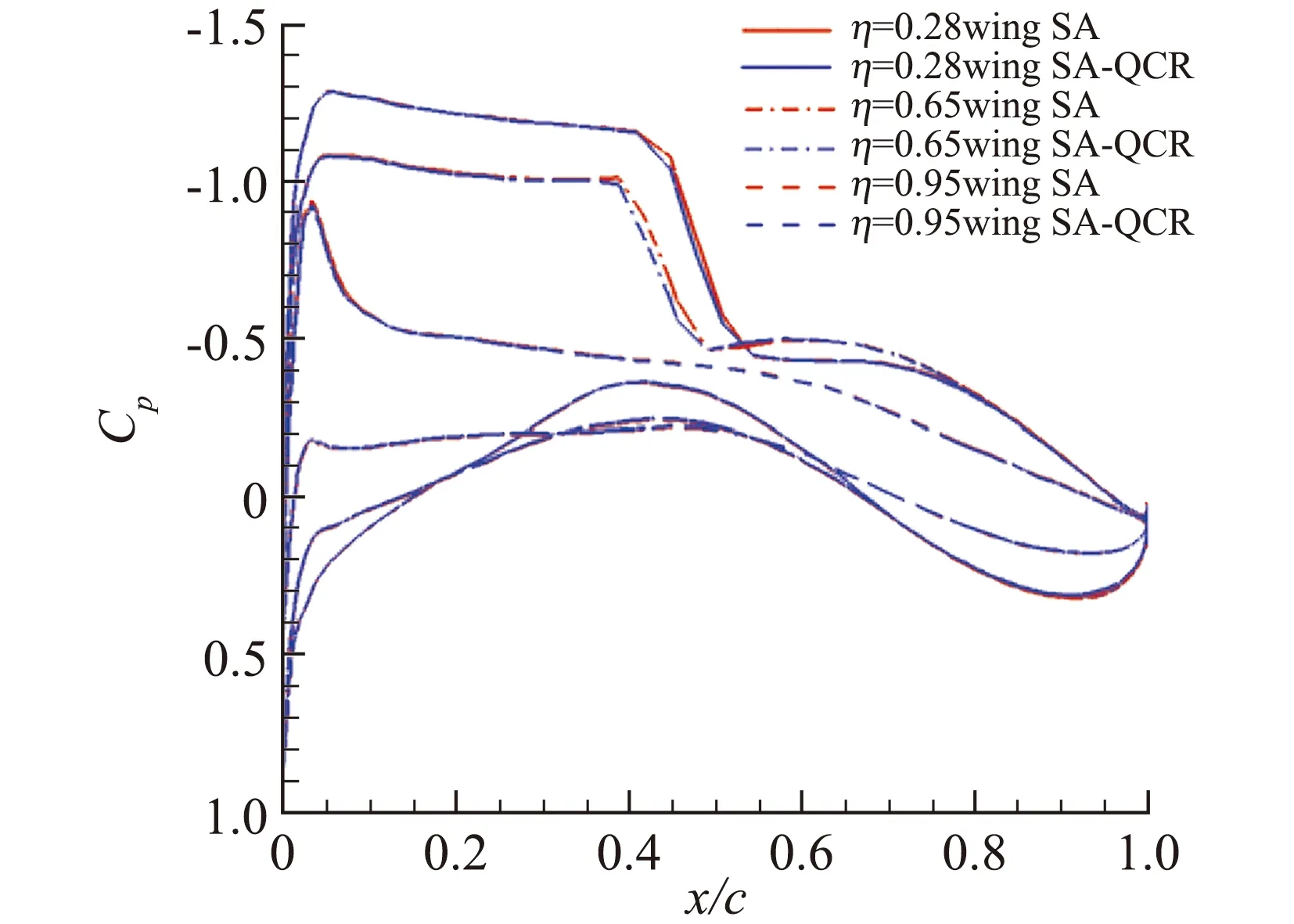
(b) Wing section group 2

(c) Wing section group 3

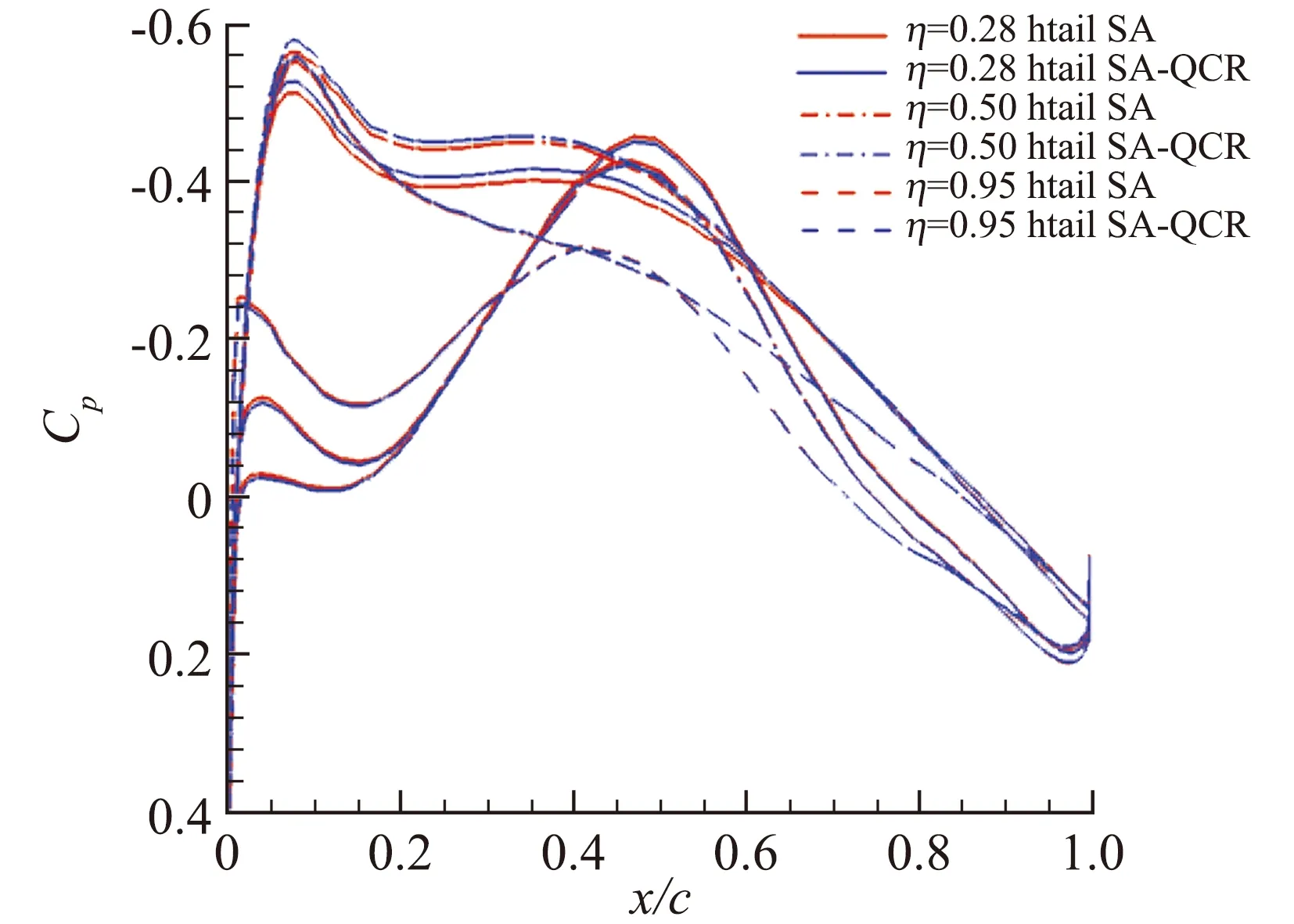
(d) Horizontal tail wing sections

综合来看，对于CHN-T1标模算例，是否考虑尾撑对气动预测精度的影响更大，而SA湍流模型是否采用QCR修正对气动预测精度的贡献不大。原因是在大迎角情况下，CHN-T1标模翼身结合处几乎不存在分离泡，因此无需使用针对拐角二次流动的QCR关系对基于Boussinesq假设的线性涡黏性模型进行修正，这与CRM标模的表现是不同的(如图11所示)。

另外，SA-QCR模型在小迎角时力矩系数实验值吻合较好，而SA模型在大迎角时力矩系数与实验值

(a) CRM(AOA=4.0°) (b) CHN-T1(AOA=4.0°)

吻合较好,其原因还有待研究。

5 结 论

根据国内第一届航空CFD可信度研讨会活动(AeCW-1)的安排，本文基于自主研发的CFD软件平台HyperFLOW对NACA0012翼型低速绕流、AeCW-1提供的客机标模CHN-T1进行了气动特性预测与可信度研究。主要结论如下：

(1) 观测精度阶和网格收敛性指数定量显示出HyperFLOW给出的数值结果具有较好的网格收敛性和可信度；

(2) 模型尾撑对力矩的预测精度影响较大，考虑尾撑影响能够得到更接近实验值的结果；

(3) 静气动弹性对气动力和力矩有一定影响，静气动弹性的引入可以一定程度提高气动力和力矩的预测精度，但是在本文中这一影响并不显著；

(4) 是否引入QCR关系式会对SA模型求解气动力矩的预测精度产生一定影响，但是并不能明显提高预测精度，这与CRM标模不同，因为大迎角时CHN-T1标模翼身结合部几乎不存在分离泡，因此无需采用QCR关系式对SA湍流模型进行修正；

(5) SA-QCR模型在小迎角时力矩系数与实验值吻合较好，而SA模型在大迎角时力矩系数与实验值吻合较好，原因还有待研究。