超低频波形信号源保护用电流互感器励磁特性试验方法

刘涛，梁仕斌

（1.云南电力技术有限责任公司，昆明 650217；2.云南电力试验研究院（集团）有限公司，昆明 650217）

0 前言

电流互感器作为电力系统的主设备之一，互感器性能不满足要求则可能引起保护装置的勿动或拒动，造成重大电网安全事故，进行互感器励磁特性试验是判断互感器性能的重要手段之一。如今随着电网的快速发展，大量新型的（比如TP类）保护用电流互感器拐点电压高达一两万伏，该电压远远超出电流互感器二次绕组匝间绝缘的耐受能力，传统的工频试验方法已经不能满足现场试验的需求，而超低频正弦波电源存在硬件设计困难、测试结果不理想的问题。超低频的方波、三角波等电源则设计简单，容易实现，因此研究基于超低频任意波形信号源进行励磁特性试验方法具有重大意义。

1 Lucas数学分析模型建立

高拐点的电流互感器用常规工频试验方法已经不能满足励磁特性试验要求，而我国相关规程也提出低频原理进行测试的方法，比如JB/T5356-2002《电流互感器试验导则》，但其中规定将二次绕组等效为线性电感，仅仅按频率关系折算，这种方法存在很大的误差，无论从理论分析和实测数据比对均证明了这一点。因此建立科学的非线性等效电路是十分重要的。

参考Lucas模型，建立如下图1所示的超低频法测试电流互感器励磁特性分析计算模型。电流互感器二次绕组漏抗非常小，小到可以忽略，励磁回路分解成涡流损耗支路、磁滞损耗等效支路和主电感支路，三条支路并联并与电流互感器二次绕组直阻串联形成整个回路。

图1 电流互感器等效数学模型

图中：Rtc为二次绕组直流电阻；U为二次绕组端电压；Utc为二次绕组励磁电势；励磁电流；IE为涡流损耗电流；IM为主电感电流；IH为磁滞损耗电流；RE为等效涡流损耗电阻；IM为主电感；RH为等效磁滞损耗电阻。

在该数学模型中对于任意频率、任意波形的信号均存在下列关系：

1）瞬时值

2）有效值

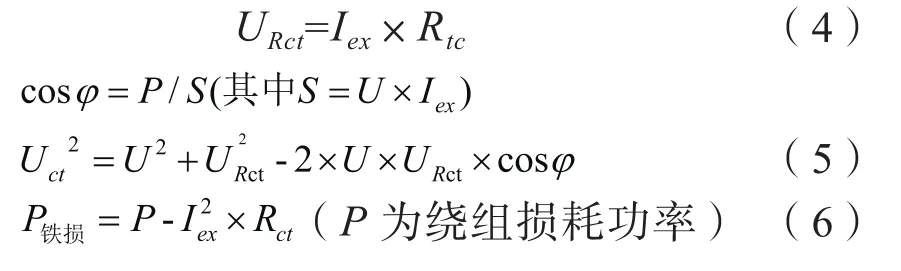
2 试验及计算方法

由公式（3）可知，任一时刻励磁电流是由主电感电流、涡流损耗电流和磁滞损耗电流相加，因此分别求出该时刻三个分量的值，即可得该时刻励磁电流瞬时值，将每个时刻的励磁电流瞬时值进行有效值计算即可得励磁电流有效值。考虑二次绕组直流电阻的影响及计算出励磁电流值可计算得出励磁电压值。下面分步阐述分析计算方法。

2.1 涡流损耗电流分离计算

在图1的模型中主电感电流iM和磁滞损耗电流iH不能单独分离出来，设其和电流为i0，i0反映在互感器的磁滞回线中（即i0－φ曲线），因此有

2.1.1 涡流损耗电流计算

等效涡流损耗电阻RE可以近似看成纯电阻且具有线性，当其两端励磁电势为utc时，涡流损耗电流在已知utc和RE时计算可得涡流损耗电流iE，测试计算RE是关键，其测试原理图如图2。

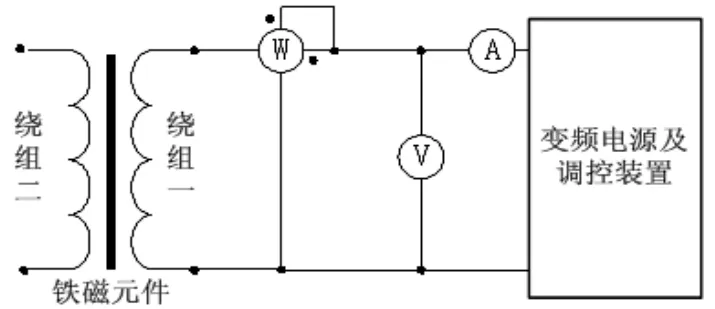
图2 涡流损耗等效电阻测试原理图

RE测量计算方法如下:

试验时按照图2接线，采用任意波形变频信号源，在两个不同频率下f1、f2测量互感器二次绕组损耗功率P1和P2、绕组端电压U1和U2和励磁电流Iex1和Iex2，并按（5）中所述计算绕组感应电势为Uct1和Uct2。根据公式列立两个独立方程式，式中f为试验时的信号源频率。

联合求解方程得到：

因此两端励磁电势为utc时涡流损耗电流瞬时值：

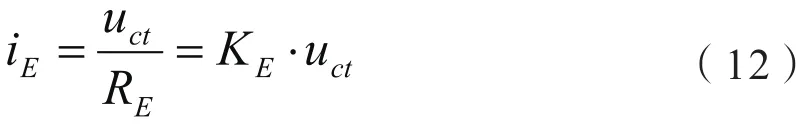
2.1.2 磁滞损耗电流i0的计算

电流互感器铁心磁滞损耗电流i0与该时刻的磁通量φ是一一对应关系，而与所施加励磁电源频率和波形无关，利用这个特性可用任意波形的周期性电源进行励磁，做出基本磁化曲线和极限磁滞回线，并利用渐近线压缩法求出任意电压对应的局部磁滞回线，在局部磁滞回线上可求得不同时刻磁滞损耗电流i0。

1）基本磁化曲线和极限磁滞回线的拟合：试验前对电流互感器进行退磁，并按照图3进行接线，选定信号源的输出电压及输出频率，使得在选定电压下互感器铁心进入深度饱和。

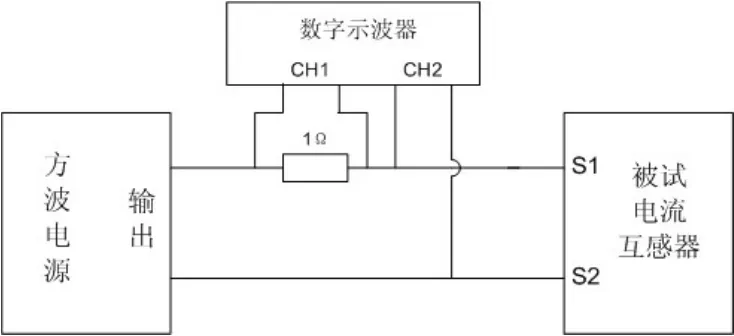
图3 磁滞损耗电流测试原理图

从合上信号源t=0时刻开始记录以i0为横坐标φ为纵坐标的曲线，基本磁化曲线是电压从0逐渐升高时每个局部磁滞回线的顶点，极限磁滞回线是铁心进入深度饱和以后最大的磁滞回线，典型曲线如图4。图4中oa段为基本磁化曲线，abcdefa闭合曲线为极限磁滞回线。

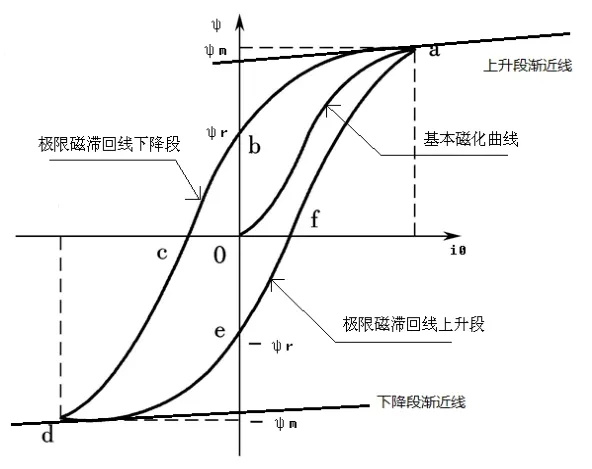
图4 基本磁化曲线和极限磁滞回线图

2）渐近线方程拟合：图4中defa段为极限磁滞回线上升段，极限磁滞回线上升段值最大2个点确定一条直线，即为上渐近线。数据代入方程φ=k1i0+b1，求解可得k1和b1。同理可以求的下渐近线方程为φ=k2i0-b2。理论上k1=k2；b1=b2。

3）局部磁滞回线的拟合：假设施加在互感器二次绕组上励磁电势为50Hz的交流电压Ua，则磁通瞬时值为利用测得基本磁化曲线，用插值法可计算出φ0所对应的i0，以点（φ0，i0）为顶点的局部磁化曲线可由极限磁滞回线defa段向上渐近线φ=k1i0+b1按比例压缩得到，压缩比例：

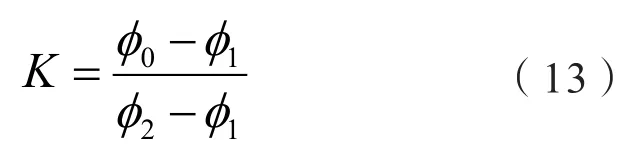
式中，φ1为电流为i0时上渐近线的磁通φ2为电流为i0时极限磁滞回线上升段对应的磁通。

当局部磁滞回线上电流为ix时，则其通过比例 K 压缩后磁通为φx=K(φ2x-φ1x)+φ1x，其中φ1x是电流为ix时上渐近线的磁通，φ2x是电流为ix时极限磁滞回线上升段对应的磁通。通过计算可以得到一组数据，即为局部磁化曲线的上升段。

同理其对称点（-i0，-φ）通过该点下降段的局部磁化曲线可由极限磁滞回线abcd通过比例压缩得到，计算得到上升段和下降段曲线相交部分即为局部磁化曲线。不同励磁电势对应不同的局部磁化曲线，典型曲线如图5。

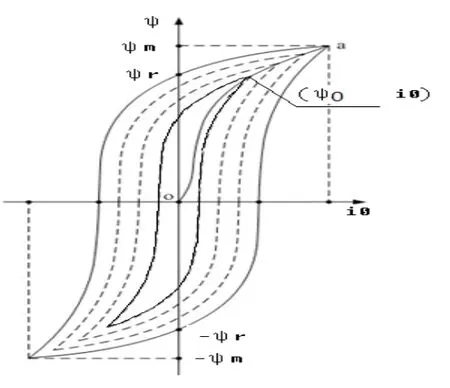
图5 不同励磁电势下的局部磁滞回线图

4）磁滞损耗电流i0的计算：假设施加在电流互感器二次绕组上励磁电势为50Hz的交流电压Ua，把一个周期分为n个相同的时间段，每个时间点的瞬时磁通用插值法按照③中方法求的每个时间点磁通对应的磁滞损耗电流i0(l)。

2.2 50Hz的交流励磁电势为下励磁电流计算

如前所假设50Hz交流励磁电势为Ua，其瞬时值为涡流损耗瞬时电流磁滞损耗瞬时值在2.1中已求出为i0(l)。由公式iex=iE+i0，可得每个时刻对应的励磁电流iex(l)=iE(l)+i0(l)，l=0,1,2,....,(n-1)n。

2.2.1 励磁电流有效值计算：

对前面计算出的离散励磁电流iex(l)按公式（14）进行有效值计算。

2.2.2 励磁电压有效值计算

综合上述可以得到励磁特性曲线上一点（Iex，U）按照此方法可得励磁特性曲线上任一点的电压和电流值。

3 分析计算方法的验证

为验证本试验分析方法的科学性和正确性，笔者对多台不同电压等级、不同型号、不同厂家的电流互感器进行超低频方波电源励磁特性测试数据与传统工频测试数据对比试验，试验对比数据及结果如下。

3.1 LRB-60型电流互感器比对数据

被试电流互感器型号为LRB-60，电流比300A/5A，额定二次负荷30 VA，准确度等级10P20，出厂编号771。本试验电源输出波形为交流方波、频率为设定为15 Hz为了更加直观比对两种方法的测试结果一致性，将两组数据绘制成励磁特性曲线放入同一坐标系进行比对，见图6。

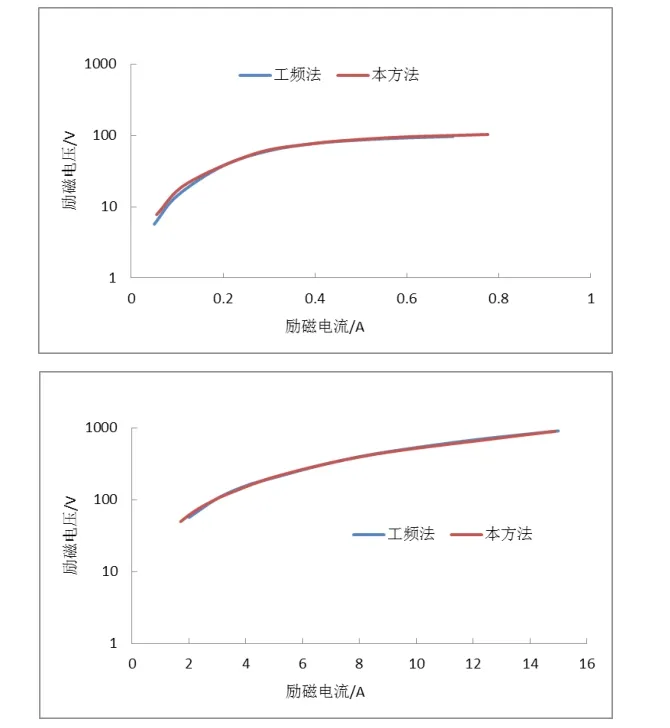
图6 本方法和工频法励磁特性曲线对比

3.2 电流互感器比对数据

被试电流互感器为某变电站51WDL断路器电流互感器，电流比为2 500 A/1 A,精确度等级为5P20。本试验电源输出波形为交流方波、频率为设定为5 Hz，数据比对见表2。将两组数据绘制成励磁特性曲线放入同一坐标系进行比，可以看出：基于超低频方波电源进行电流互感器励磁特性试验的试验、分析计算数据与工频条件下实测数据一致性良好。

4 结束语

所述方法将励磁特性试验中信号源扩展为任意周期性信号，通过涡流损耗电流和磁滞损耗电流的分离并且分别测量计算，考虑直流电阻影响，最终推算出电流互感器励磁特性曲线。不仅解决了传统工频试验方法电压高、设备容量大的问题，还为低频变频试验方法另辟蹊径，进一步的研究可将本文方法推广至电力系统中所有铁磁元件性能测试中。

由于本文中推导计算过程中使用了大量瞬时值数据，计算量非常大，适合编程进行数据处理。