Maple软件动画功能在高等数学教学中的应用示例
刘兴元
(邵阳学院 理学院,湖南 邵阳,422400)
旋转曲面[1]是二次曲面中的一个重要的内容,传统教学模式下的教学过程如下:
定义1 一条平面曲线C绕着该平面内的一定直线l旋转一周所形成的曲面,叫做旋转曲面,曲线C称为旋转曲面的母线,直线l叫做旋转曲面的轴。
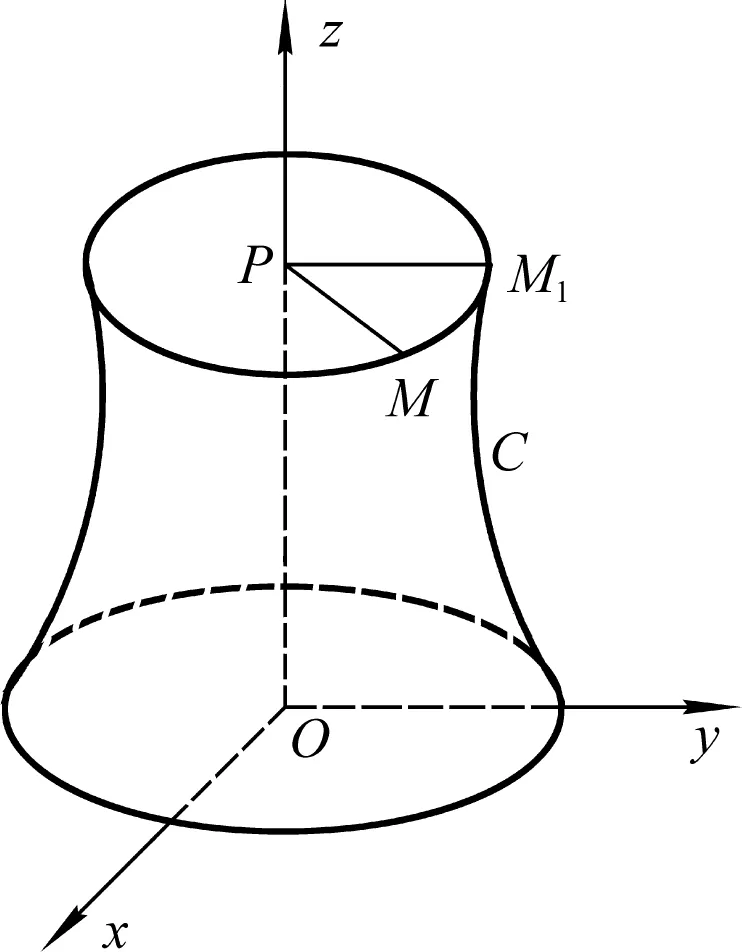
图1 旋转曲面示意图Fig.1 Schematic diagram of a rotating surface
为方便起见,仅考虑旋转轴l为坐标轴的情形。
设在yoz面上有一已知曲线C,它的方程为f(y,z)=0,将这曲线绕z轴旋转一周,就得一个以z轴为轴的旋转曲面,见图1。
在旋转曲面上任取一点M(x,y,z),设这一点是母线C上的点M1(0,y1,z1)绕z轴旋转而得到的,显然有
(1)
因为点M1在曲线C上,所以
f(y1,z1)=0
(2)
将(1)代入(2)得
(3)
(3)式即为yoz平面上的曲线f(y,z)=0绕z轴旋转而得到的旋转曲面的方程。
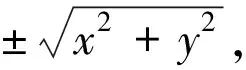
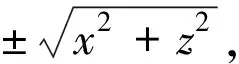
对于其他坐标面上的曲线,绕该坐标面内的任一坐标轴旋转所得到的旋转曲面方程可用类似的方法求得。
讲完上述内容及例题后,发现学生对所学的内容掌握不够,具体表现为不能熟练求得旋转曲面的方程,更不能较好地绘制旋转曲面的图形。究其原因是学生缺乏空间想象能力,对旋转曲面的定义和图形理解不够透彻。而Maple软件[2]具有强大的绘图功能,其辅助教学功能也有独到之处,可以利用其Animate命令制作动画,生动、形象展示旋转曲面的形成过程及旋转曲面的图像。文中利用Maple软件的动画功能和多媒体进行辅助教学,通过几年的教学实践,都能收到较好的教学效果。下面举例说明Maple软件的动画功能在旋转曲面教学中的独特作用。
1 Maple的动画命令在旋转曲面教学中的应用示例
例1 确定zox面上的直线z=x绕z轴旋转一周所得旋转曲面(圆锥面)方程,并用动画做出其图形。
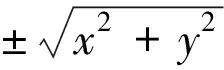
即
z2=x2+y2。
在Maple命令窗口中输入动画制作命令[4-6]
>restart:with(plots):f:=u→u:K:=180:
for i to K do ti:=3*i*Pi/K:
qumain[i]:=plot3d([u*sin(t),u*cos(t),f(u)],u=-2..2,t=0..ti)end do:
L:=display(seq(qumain[i],i=1..K),insequence=true):
x_axis:=plot3d([u,0,0],u=-2..2,v=0..1,axes=normal,labels=[x,y,z]):
y_axis:=plot3d([0,u,0],u=-2..2,v=0..1):
z_axis:=plot3d([0,0,u],u=-4..4,v=0..1):
xyz:=display(x_axis,y_axis,z_axis,thickness=3):
display(L,L,xyz,scaling=constrained,axes=normal,lightmodel=light2,orientation=[40,70],tickmarks=[2,2,4]);
运行上述命令后,在Maple工作窗口中出现动画基图,如图3所示.在Maple工作窗口中单击基图,在工作窗口的上方出现maple动画播放工具,如图2所示。

图2 maple动画播放工具Fig.2 Maple animation playback tool
在基图3中显示有符合学习习惯的空间直角坐标系和zox平面上的母线z=x,旋转轴为z轴,在Maple命令窗口中,选中图3,单击动画控制工具条中的“插放”按钮,可以观看旋转锥面的动画形成过程。若要降低旋转速度,可以将图2中旋转速度每秒10帧,通过其右侧的下调按钮减少数字值,比如调整为每秒5帧。也可选择“分帧播放”按钮(左起第四个),图4是其第72帧的形状,插放完毕即得旋转锥面的图形,见图5。

图3 圆锥面基图Fig.3 Base graph of a conical surface
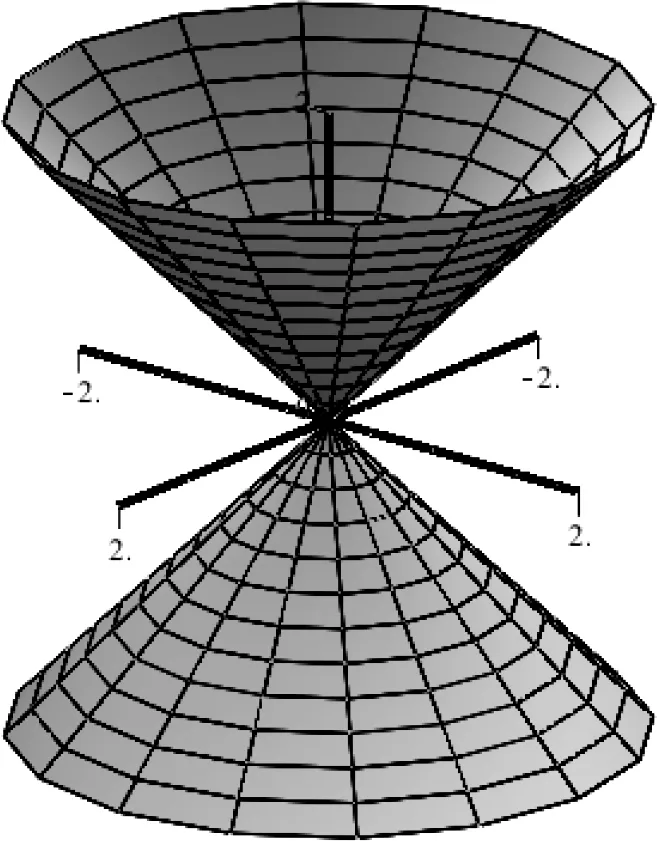
图5 旋转锥面图Fig.5 Rotational cone diagram
例2 求zox平面上的抛物线z=x2绕z轴旋转所得旋转抛物面的方程,并做其动画图形。
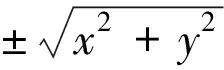
z=x2+y2。
在Maple命令窗口中输入动画制作命令
>restart:
with(plots):
x_axis:=plot3d([u,0,0],u=-2..2,v=0..1):
y_axis:=plot3d([0,u,0],u=-2..2,v=0..1):
z_axis:=plot3d([0,0,u],u=0..6,v=0..1):
xyz:=display(x_axis,y_axis,z_axis,thickness=3):
a1:=spacecurve([t,0,t^2],t=-2..2,color=red,thickness=4):
a2:=animate(plot3d,[[sqrt(s)*cos(t),sqrt(s)*sin(t),s],s=0..4,t=0..x],x=0..2*Pi,axes=normal,labels=[x,y,z]):
display(xyz,a1,a2);
运行上述命令即得动画基图(如图6)。
在基图6中有三条坐标轴和zox平面上的母线z=x2,旋转轴为z轴,在Maple窗口中,选中图6,然后点击动画控制工具条中的“分帧插放”按钮,图7是其第14帧的形状,图8是插放完毕所得旋转抛物面的图形。
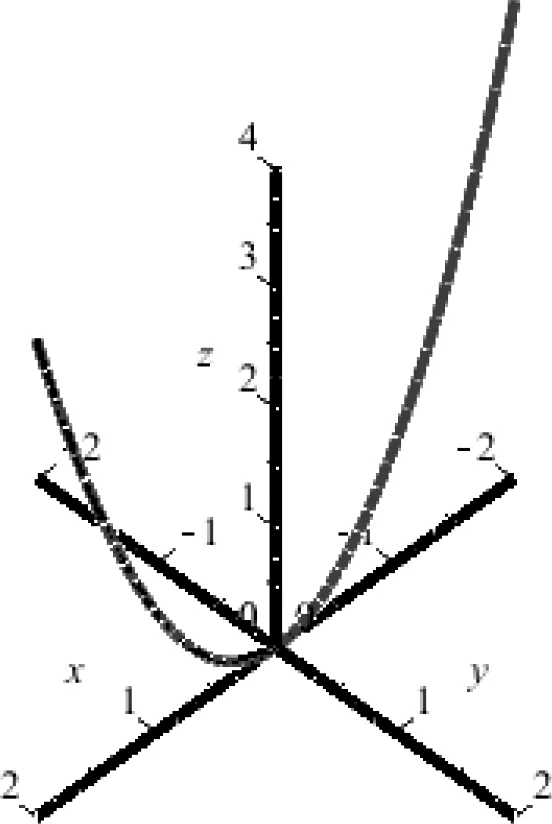
图6 旋转抛物面基图Fig.6 Base graph of a revolution paraboloid
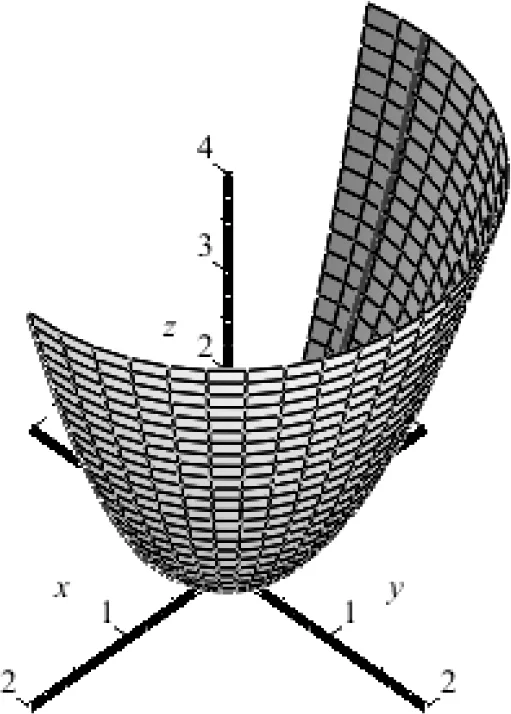
图7 旋转抛物面分帧显示图Fig.7 Framing display of a revolution paraboloid

图8 旋转抛物面Fig.8 Diagram of a revolution paraboloid
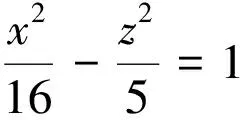
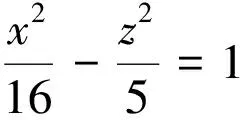
在Maple命令窗口中输入动画制作命令
>restart:with(plots):
x_axis:=plot3d([u,0,0],u=-10..10,v=0..0.01,thickness=3,axes=normal,labels=[x,y,z]):
y_axis:=plot3d([0,u,0],u=-6..6,v=0..0.01,thickness=3):
z_axis:=plot3d([0,0,u],u=-16..16,v=0..0.01,thickness=3):
xyz:=display(x_axis,y_axis,z_axis,thickness=3):
a1:=animate(plot3d,[[4*sqrt(1+(1/5)*s^2)*cos(t),4*sqrt(1+(1/5)*s^2)*sin(t),s],s=-6..6,t=0..y],y=0..2*Pi):
a2:=animate(plot3d,[[-4*sqrt(1+(1/5)*s^2)*cos(t),-4*sqrt(1+(1/5)*s^2)*sin(t),s],s=-6..6,t=0..y],y=0..2*Pi):
display(a1,a2,xyz);
运行上述命令即得动画基图(如图9)。
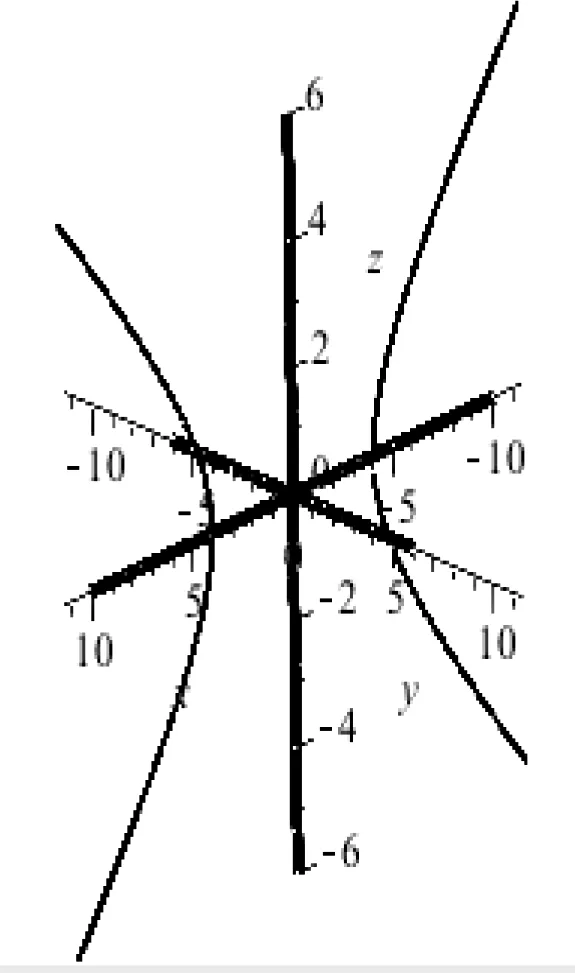
图9 旋转单叶双曲面基图Fig.9 Base graph of a hyperboloid of one sheet of revolution
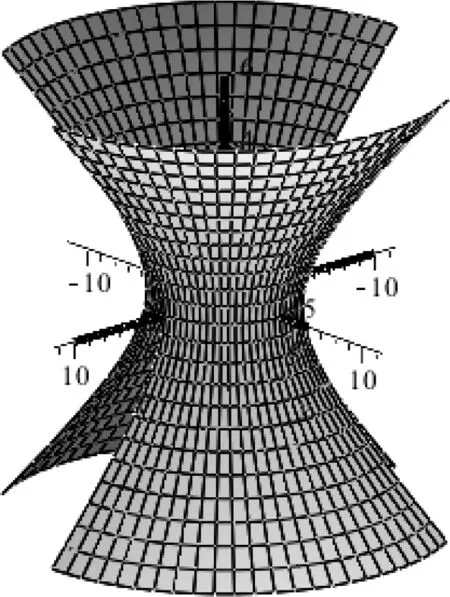
图10 旋转单叶双曲面基分帧显示图Fig.10 Framing display of a hyperboloid of one sheet of revolution
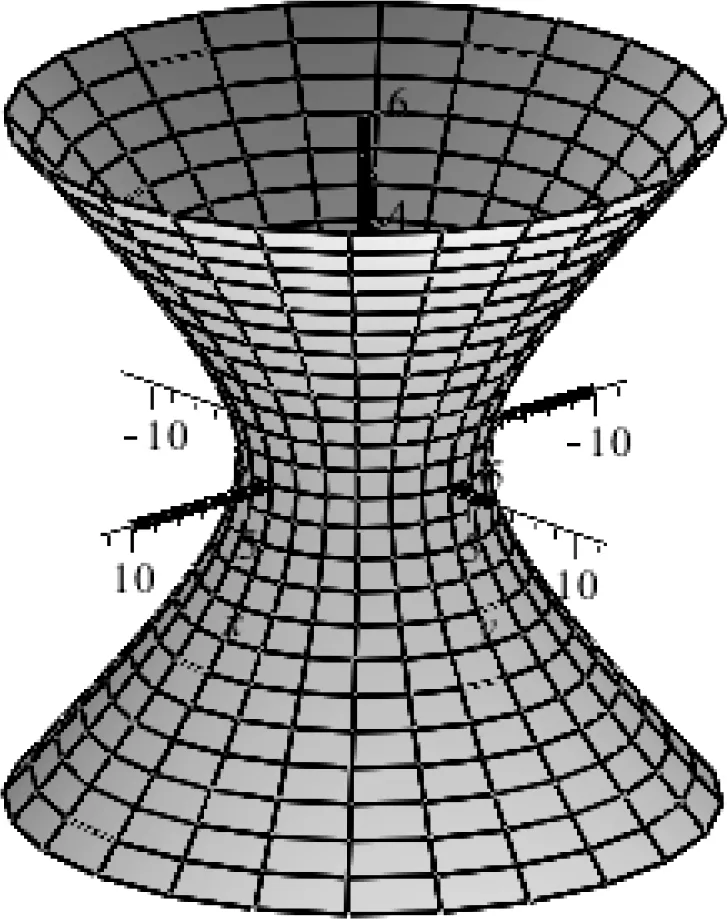
图11 旋转单叶双曲面Fig.11 Diagram of ahyperboloid of one sheet of revolution
例4 作zox平面上的双曲线z2-x2=1绕z轴旋转所得旋转双叶双曲面的动画图形。
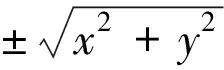
z2-x2-y2=1。
在Maple命令窗口中输入动画制作命令
>restart:with(plots):
x_axis:=plot3d([u,0,0],u=-4..4,v=0..0.01,thickness=3,axes=normal,labels=[x,y,z]):
y_axis:=plot3d([0,u,0],u=-3..3,v=0..0.01,thickness=3):
z_axis:=plot3d([0,0,u],u=-6..6,v=0..0.01,thickness=3):
xyz:=display(x_axis,y_axis,z_axis,thickness=3):
b1:=animate(plot3d,[[sqrt(s^2-1)*cos(t),sqrt(s^2-1)*sin(t),s],s=1..5,t=0..y],y=0..2*Pi):
b2:=animate(plot3d,[[-sqrt(s^2-1)*cos(t),-sqrt(s^2-1)*sin(t),s],s=1..5,t=0..y],y=0..2*Pi):
b3:=animate(plot3d,[[sqrt(s^2-1)*cos(t),sqrt(s^2-1)*sin(t),s],s=-1..-5,t=0..y],y=0..2*Pi):
b4:=animate(plot3d,[[-sqrt(s^2-1)*cos(t),-sqrt(s^2-1)*sin(t),s],s=-1..-5,t=0..y],y=0..2*Pi):
display(b1,b2,b3,b4,xyz);
运行上述命令即得动画基图(如图12)。
在基图12中有三条坐标轴和zox平面上的母线z2-x2=1,在Maple窗口中,选中图12,然后单击动画控制工具条中的“插放”按钮,可以观看旋转双叶双曲面的形成动画过程,插放完毕即得旋转双叶双曲面的图形,见图14,也可选择“分帧播放”按钮,图13是其第10帧的形状。
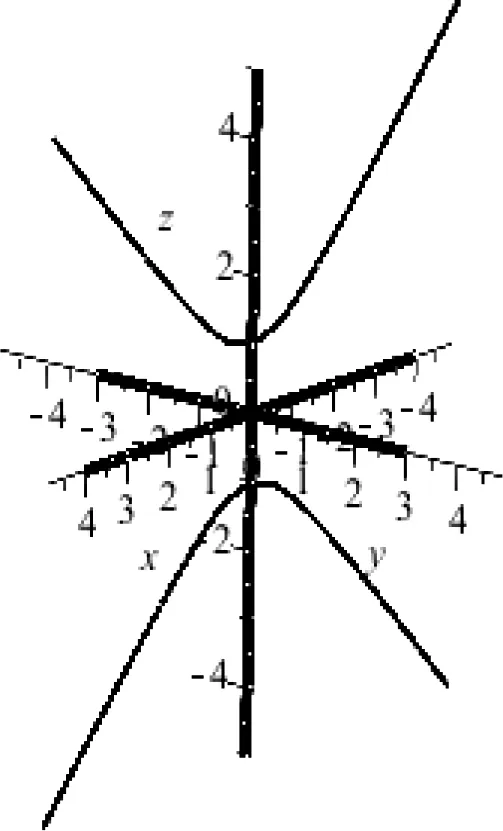
图12 旋转双叶双曲面基图Fig.12 Base graph of a hyperboloid of double sheets of revolution

图13 旋转双叶双曲面基图Fig.13 Framing display of a hyperboloid of double sheets of revolution
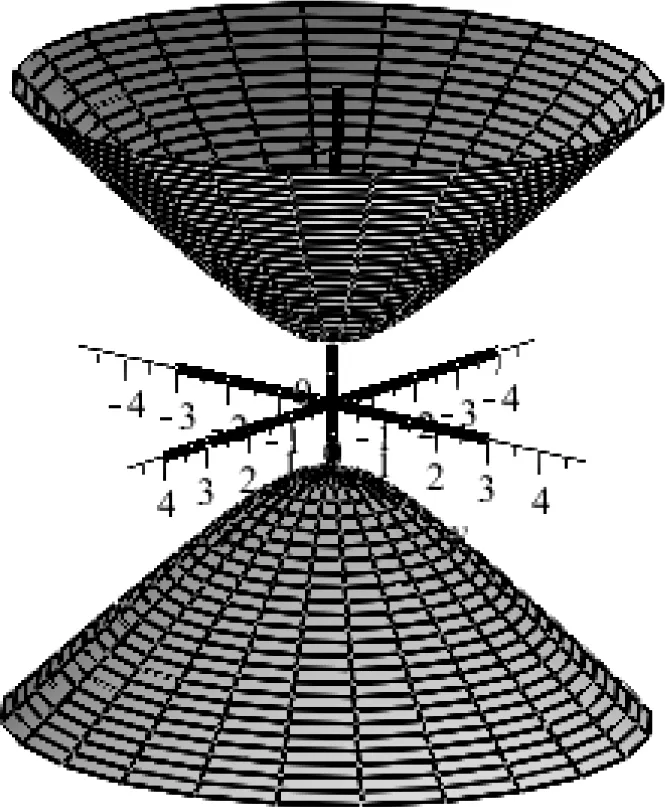
图14 旋转双叶双曲面Fig.14 Diagram of ahyperboloid of double sheets of revolution
例5 作zox平面上的曲线x=1+sinz(0≤z≤2π)绕z轴旋转所得旋转曲面的动画图形。
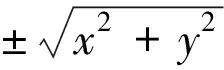
x2+y2=(1+sinz)2。
在Maple命令窗口中输入动画制作命令
>restart:
with(plots):
animate(plot3d,[[(sin(t)+1)*cos(s),(sin(t)+1)*sin(s),t],s=0..(1/1000)*2^Pi*i,t=0..2*Pi],i=1..1000,axes=normal,labels=[x,y,z]);
运行上述命令即得动画基图(如图15)。
在Maple窗口中,选中图15,然后单击动画控制工具条中的“插放”按钮,可以观看旋转曲面的形成动画过程。插放完毕即得旋转曲面的图形,见图17,也可选择“分帧播放”按钮,图16是其第14帧的形状。
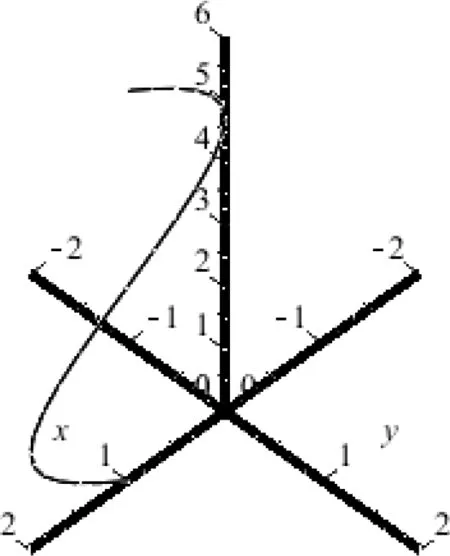
图15 旋转正弦曲面基图Fig.15 Base graph of a rotating sine surface
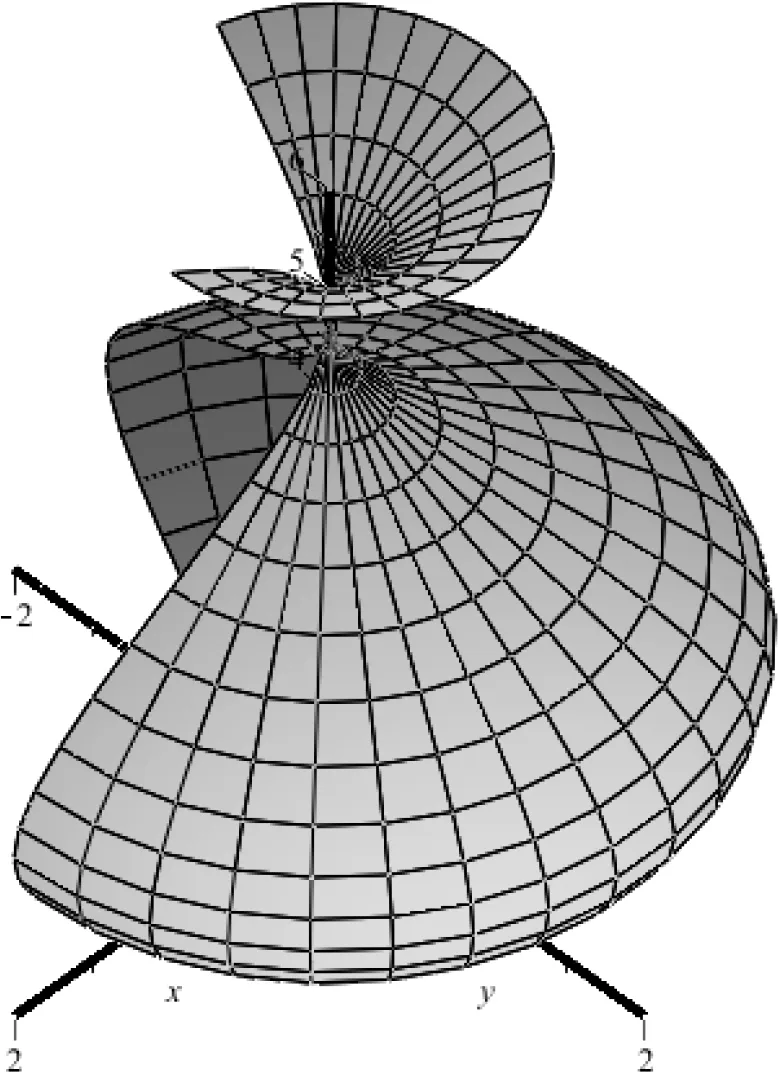
图16 旋转正弦曲面分帧图Fig.16 Framing display of a rotating sine surface
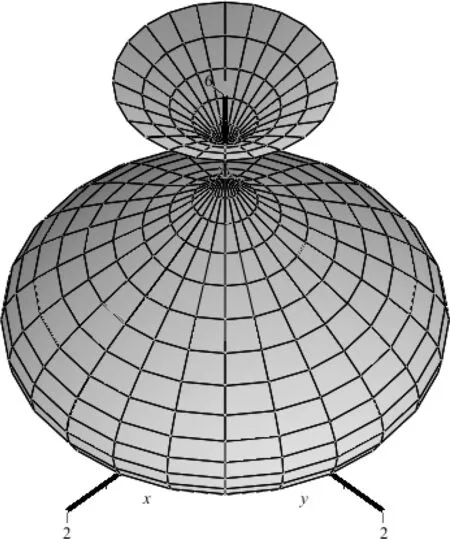
图17 旋转正弦曲面Fig.17 Diagram of a rotating sine surface
2 结语
文中通过5个例子,介绍了圆锥面,旋转抛物面,旋转单叶双曲面,旋转双叶双曲面等旋转曲面的动画制作命令,在多媒体教学中,可以切换到Maple平台,演示上述动画。也可以在Maple平台下将各旋转曲面的基图存贮为gif格式文件,并将此gif格式文件粘贴到PowerPoimt课件的幻灯片中,播放幻灯片就可以看到旋转曲面形成的旋转动画,然后再讲述旋转曲面定义并求各种旋转曲面的方程,将起到事半功倍的作用。

