全正矩阵的多水平预处理子
刘仲云,周孜
(长沙理工大学 数学与统计学院,湖南 长沙,410114)
文中考虑用CG型方法求解全正线性方程组
Ax=b
(1)
其中A=[ai,j]∈Rn×n(i,j=1,2,…,n)为全正矩阵。
全正矩阵是一类特殊的结构矩阵,目前已有一些相关的理论与算法的研究[1-6]。
全正线性方程组的解法可分为直接解法和迭代解法,直接法即通过Neville消元法将系数矩阵分解为一系列下双对角矩阵、对角矩阵和一系列上双对角矩阵的积,进而求解方程组[5]。关于这一类的方程组的迭代解法的研究不多,CARNICER等[3]在2010年提出了的Richardson迭代方法解全正矩阵线性方程组,该方法证明了对任何的全正矩阵,一个松弛的Richardson迭代法是收敛的。
一般来说,直接解法主要适用于小规模问题。对于大型问题,直接解法计算量太大且数值不稳定,而迭代解法数值稳定且易于并行计算。所以文中考虑用迭代解法求解全正线性方程组。众所周知,一个好的预处理子可以使CG型方法具有戏剧性的收敛性。
1 预备知识
首先给出几个定义及引理。
定义1.1[3]如果一个矩阵的任意阶子式都是非负的,那么该矩阵称为全正矩阵。


定义1.3[5]设A是m×n阶矩阵,而B是p×q阶矩阵,则A和B的Kronecker积A⊗B是一个(m·p)×(n·q)阶矩阵
引理 1.2[5]如果有λ(A)={λ1,…,λm},λ(B)={μ1,…,μm},则A,B矩阵的Kronecker积的特征值可以表示为
λ(A⊗B)={λiμii=1,2,…m;j=1,2,…,n}
另外,如果A,B都为全正矩阵,则A⊗B也为全正矩阵。
2 多水平预处理子
记{A(k)k=0,1,…l}是一个矩阵序列,Dk是k水平上所对应的行标的集合。
首先,定义
A(0)=A
将矩阵A(0)进行分块:
这里

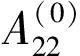

基于以上序列,构造一系列多水平预处理子{M(k)}。
首先,构造A(l)的预处理子
(3)
这里
是S(l)的近似矩阵。
则当k=l-1,l-2,…,0时,与此类似,直到k=0,
(4)
这里
易知,在每一个水平上构造的预处理矩阵[M(k)](k=0,1,2,…,l)是非奇异的。
3 数值实验
下面的数值实验例子是曲面拟合中两个经典的例子。因为系数矩阵不正定,所以通常用共轭梯度法求解下面的预处理线性方程组:
(M-1B)T(M-1B)x=(M-1B)TM-1b
(5)

(6)
对应于曲面拟合的配置矩阵为A=Bn⊗Bm。
例6 令Sn是由Said-Ball基Si(t)在区间[0,1]上生成全正矩阵,这里
(7)
当n是偶数的时候,
此处⎣k」表示小于或等于k的最大整数,「k⎤表示大于或等于k的最小整数。
则对应于曲面拟合的配置矩A=Sn⊗Sm。

表1 CG解例5时所用迭代次数
Tabel 1 The iterations for example 5by CG method

nP=IP=M(m,l)48442438(88,2)67654525(145,2)72945322(160,2)84179552(137,4)96195096(116,6)1 02489984(67,14)
表2 CG解例6时所用迭代次数
Tabel 2 The iterations for example 6by CG method

nP=IP=M(m,l)3261(3,4)169177(16,4)225162(15,3)441181(25,14)676191(44,14)729192(44,14)

由以上表格可以看出,经过预处理后的迭代步数远远小于没有进行预处理的迭代步数。
为了进一步说明其有效性,文中描绘出了例5当n=484,例6当n=169时,对应的预处理矩阵的谱分布图,如下图所示,可以看出加了预处理子矩阵的谱更加聚集,从而也说明该预处理子的有效性。

图1 例5中n=484预处理矩阵的谱分布图Fig.1 The spectral distribution of preconditioned matrix for example 5 when n=484

图2 例6中n=169预处理矩阵的谱分布图Fig.2 The spectral distribution of preconditioned matrix for example 6 when n=169

