基于半参数模型的水准网平差

雷前坤，张俊

(贵州大学矿业学院，贵州 贵阳 550025)

1 引 言

在水准测量中，受观测条件的影响，观测值中常常含有系统误差。当系统误差小于或至多等于偶然误差的量级时，通常不考虑系统误差对观测值的影响[1]。目前主要采用经典最小二乘对水准网进行平差处理，利用该方法进行水准网平差时只能顾及偶然误差对观测值平差结果的影响，而无法顾及系统误差的影响。当系统误差较大时，继续采用经典最小二乘进行平差，将得不到可靠的参数估值，甚至会产生错误结论[2]。半参数模型是统计学界在20世纪80年代提出的，并被引用到测量领域进行测量数据处理，在模型精化、系统误差分离和减弱方面得到了广泛应用[3]。文献[2～7]对半参数模型从多个方面进行了讨论，证明了半参数模型在某些测量数据处理方面相对于经典最小二乘具有更高的理论精度。本文尝试利用半参数模型来对水准网进行平差，并将平差结果与经典最小二乘的平差结果进行对比分析，得出有益结论。

2 半参数平差模型的原理及解算过程

2.1 半参数平差模型的原理

半参数平差模型可以表示为[2]：

L=BX+S+△

(1)

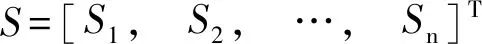
半参数平差模型中既含有参数分量，又含有非参数分量，参数分量用以表示参数与观测值之间确定的函数关系，而非参数分量则表示系统误差或模型误差与观测值之间不确定的函数关系。若系数矩阵B=0，则半参数平差模型变为非参数模型；若模型误差S=0，则半参数平差模型变为线性参数模型。因此，半参数平差模型是参数模型与非参数模型的混合模型[4，5]。

根据式(1)可以写出半参数平差模型的误差方程：

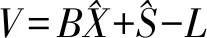
(2)

根据最小二乘原理有

(3)

式中，P为正定方阵，是观测值L的权阵；R是一个适当给定的正定矩阵，称为正规化矩阵，R的选择与具体问题有关；α是一个给定的纯量因子，称为平滑因子(或称平滑参数)，极小化过程中在S和V之间起到平滑的作用。

根据式(2)、式(3)通过构造拉格朗日函数解算可得半参数平差模型的法方程：

(4)

将法方程式(4)写成下列形式

(5)

(6)

令N=BTPB，由于N可逆，于是有

(7)

将式(7)代入式(6)经过整理得：

(8)

令M=P+αR-PBN-1BTP，则可得到

(9)

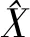
(10)

式中，H(α)=s+(I-s)B[BTP(I-s)B]-1BTP(I-s)，其中s=(P+αR)-1P。

从上述半参数平差模型的解算过程中不难看出，解算半参数平差模型的关键和核心是如何合理的构造正规化矩阵R和选择平滑因子α。正规化矩阵R的构造方法归纳起来主要有构造矩阵法、样条函数法和时间序列法等，平滑因子α的选择方法主要有广义交叉核实分值函数法、信噪比值法、L-曲线法等[7]。本文中正规化矩阵R采用时间序列法来构造，平滑因子α采用L-曲线法中的最小距离法来求解。

2.2 正规化矩阵R的构造

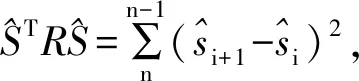
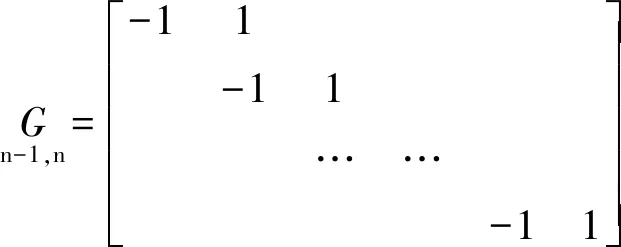
(11)

则可取：

R=GTG

(12)

2.3 平滑因子α的求解

NN(α)=VT(α)PV(α)

从上列两加权范数可以看出，当平滑因子α取不同的值时，可以得到不同的SN(α)和NN(α)，以SN(α)为横坐标，NN(α)为纵坐标画图，可以得到许多不同的点对(SN(α)，NN(α))。将这些点进行曲线拟合，可以得到一条形状像“L”的光滑曲线，称之为“L-曲线”。用该曲线来求解平滑因子α的方法叫作“L-曲线法”。用“L-曲线法”来求解平滑因子有两种方法，最短距离法和最大曲率法，即曲线上曲率最大的点所对应的α或曲线上到坐标原点最近的点所对应的α即为所要求的平滑因子的值，本文中采用最小距离法来求解平滑因子α。用最短距离法求解平滑因子α的步骤如下：

(1)通过黄金搜索法来确定平滑因子α的取值范围；

(2)在平滑因子α的取值范围内，每取一个α值，进行一次平差计算，求出一组(SN(α)，NN(α))，通过取不同的α值，分别进行一次平差计算，得到许多组(SN(α)，NN(α))，将这些点进行曲线拟合，则曲线上距离原点最近的点对应的α即确定为最终的平滑因子。

3 算例分析

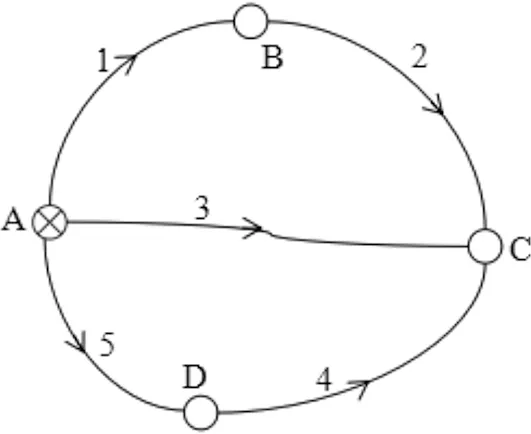
图1 水准网

水准路线观测值 表1

采用经典最小二乘和半参数模型对高差观测值进行平差。

(1)列误差方程

(2)计算各高差观测值的权

取10 km的观测高差为单位权观测，即按：

定权，得观测值的权阵为：

经典最小二乘平差的计算结果：

半参数平差模型的计算结果：

精度统计 表2

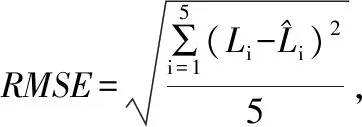
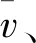
4 结 语

文中针对经典最小二乘平差无法顾及水准网中系统误差这一问题，采用半参数模型来对水准网进行平差并获得了优于经典最小二乘的平差结果。半参数模型中含有描述系统误差的非参数分量，在平差过程中顾及到了系统误差对观测值平差结果的影响，因此所得平差结果的精度要优于经典最小二乘平差。