基于SRTM的区域平面独立坐标系建立方法研究

范清彪，李江卫，孙伟，姚鹏，吴多

(武汉市测绘研究院，湖北 武汉 430022)

1 引 言

随着城市建设和社会经济的发展，人们对高精度地理信息数据的需求越来越迫切。由于传统技术的限制，以往使用的1954年北京坐标系及1980西安坐标系均为参心坐标系，无法满足现代测绘的需求。现代卫星大地测量技术的发展，使建立高精度大地坐标系成为可能，为此我国自主建立了适应现代空间技术发展、满足经济建设需求的新一代大地坐标系—2000国家大地坐标系(China Geodetic Coordinate System 2000，简写CGCS2000)[1]。

虽然我们处于三维空间中，但实际城市建设、规划管理和工程施工都习惯采用统一的平面坐标系及高程系统，因此通常需要按照一定的投影方式建立区域相对独立的平面直角坐标系。该平面坐标系应方便与国家统一大地坐标系建立联系，同时更好地满足实际应用需求。

根据《城市坐标系统建设规范》[2]，城市平面坐标系必须采用高斯投影，其定义包括参考椭球的选择、中央子午线的选择、投影面高程的选择和坐标系原点和定向的确定。为方便城市建设，城市平面坐标系的选择和定义应以投影长度变形值不大于 2.5 cm/km(相对误差小于1/40000)为原则，并根据地理位置和平均高程确定。为保证与国家大地坐标系的统一，城市平面坐标系的参考椭球及定向通常与国家大地坐标系保持一致。中央子午线确定后，城市平面坐标系的原点及定向也可相应确定。因此城市平面坐标系的建立关键在于确定中央子午线及投影面高程(即高程抵偿面)。

当城市地形起伏较小(如平原地区)，通常取该城市的中央经线作为投影中央子午线，取其平均高程面作为高程抵偿面。当一个地区东西跨度较大时(如超过 90 km)，通常选取双中央子午线或多投影高程面的投影方式[4]。但当一个地区地形起伏较大时，如丘陵、山地地区，即使东西跨度不大，难以选择一个确定的中央子午线及高程抵偿面，使得所有地区都满足投影长度变形值不大于 2.5 cm/km的要求。这时需要根据当地实际地形及开发利用情况确定最佳的平面坐标系建立方案。以往的选择方法大多基于该地区控制点成果进行计算分析[5]，而控制点一般数量有限、分布不一定均匀，无法客观反映真实的城市地形情况及建设发展需求。本文提出了一种基于高分辨率DEM数据，顾及城市建设发展需求，综合确定城市平面坐标系最佳中央子午线和高程抵偿面的方法，对于建立与CGCS2000相联系的区域平面独立坐标系具有一定的示范和借鉴作用。

2 投影长度变形分析

将地面实际测量长度投影到平面坐标系，需要经过高程归化改正和高斯投影变形计算两步，即：

(1)

(2)

式(1)为高程对长度投影变形的影响，式(2)是高斯投影对长度投影变形的影响。式中：ym为地面边两端点近似横坐标平均值，单位为m；Rm为参考椭球面在地面边中点的平均曲率半径，单位为km；Hm为归算边高出参考椭球面的平均高程。综合以上两式，经过高程归化和投影改化，忽略高阶项的影响，边长变为：

(3)

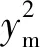
依据《城市坐标系统建设规范》，当高程归化和高斯投影的综合影响不超过 2.5 cm/km时，优先采用国家3°带高斯投影。而当长度综合变形值大于 2.5 cm/km时，城市坐标系可依次采用：具有高程抵偿面的3°带高斯投影；任意带高斯投影；具有高程抵偿面的任意带高斯投影。

3 基于高分辨率DEM数据的平面坐标系建立方法

为建立合适的区域平面独立坐标系，通常利用该区域范围内的控制点来进行投影变形计算分析，以确定中央子午线和高程抵偿面。但控制点分布稀疏，无法保证其分布能够代表该地区的地形特征，也不能与城市建设发展的需求相契合。本文利用高分辨率的DEM数据(SRTM数据)进行长度投影变形计算与分析。SRTM数据主要是由美国航空航天局(NASA)和国防部国家测绘局(NIMA)联合测量的，全称Shuttle Radar Topography Mission。SRTM数据有1″×1″(30 m)和3″×3″(90 m)两种空间分辨率。1″×1″SRTM数据在95%置信度的标称精度为 ±16 m，经与测高卫星比对研究[5]，在我国区域误差介于 -16.135 m～16.135 m之间占94.8%，整体精度优于 9 m，在平原盆地地区精度为 4 m～5 m，在高原、山地、丘陵地区精度为 8 m～12 m，而抵偿高程面通常以 10 m的整倍数进行选取，因此SRTM数据精度完全满足本文中实验要求。在实际应用中，如有更高精度DEM数据，可尽量采用。

因此本文基于1″×1″SRTM数据计算区域的每公里长度投影变形值，然后采用最优化条件准则，通过遍历搜索来确定区域最佳中央子午线和高程抵偿面。最优化条件可表示为：

(4)

其中△Si为第i个地形点对应的每公里长度投影变形，PH(i)为基于地形高程设定的权值，一般在丘陵、山地地区，城市建设主要在海拔较低的河谷地区，可设置较大权值，而高海拔地区设置较低权值；如当一个城市主要建设区在高程 100 m以下时：

(5)

Pw(i)为基于城市建设发展需求设定的权值，如根据城市规划重点建设区设置较高权值，而自然保护区等开发较少的地方设定较小权值。Pw(i)、PH(i)可以同时综合使用，也可以单独使用。投影分析时，可按照一定高程间隔(如 10 m)和中央子午线间隔(如5′)对高程抵偿面和中央子午线进行遍历搜索，以确定最优高斯平面投影方案。

4 实例应用

本文以武汉市及崇阳县为例，基于高分辨率SRTM数据，进行长度投影变形分析，给出相应平面独立坐标系的最优建议方案，采用的椭球与CGCS2000保持一致。

4.1 崇阳县投影变形分析

崇阳县经度范围为东经113°43′～114°21′，东西向跨度小于 70 km，但县域范围内地形起伏较大，海拔变化范围为几十米～1000 m，如1图所示，图中蓝色区域海拔为 0 m～100 m，绿色区域海拔为 100 m～200 m，黄色区域海拔为 200 m～1 000 m。国家统一3°带114°E中央子午线与整个县域中央经线非常接近。114°E中央子午线位于县城西侧，靠近主城区(图1中红色五角星位置)。为顾及与2000国家大地坐标系的衔接及使用的方便性，以114°E作为中央子午线，采用式(4)及式(5)作为最优化条件确定最佳高程抵偿面。根据卫星影像及DEM高程分布图显示，崇阳县主要建设区在海拔 100 m以下，因此这里仅根据PH设置权值，将 100 m作为设置权重的阈值，高程低于 100 m时，设为等权W0，高程超过 100 m时，设置为与高程值的平方成反比，计算时纳入了 30 m分辨率SRTM模型中高程点共 265 226个。图2为设置不同高程抵偿面Hp及W0值时，每公里长度投影变形加权平方和Sd的变化示意图。

由图2可以看到，当W0逐渐增大时，最优高程抵偿面值逐渐减小，当W0增大至一定程度时，最佳高程抵偿面为 -80 m(即将投影面抬高 80 m)，且基本不再变化。图3为分别采用 0 m、-60 m、-80 m和-100 m高程抵偿面时，每千米长度投影变形分布图。

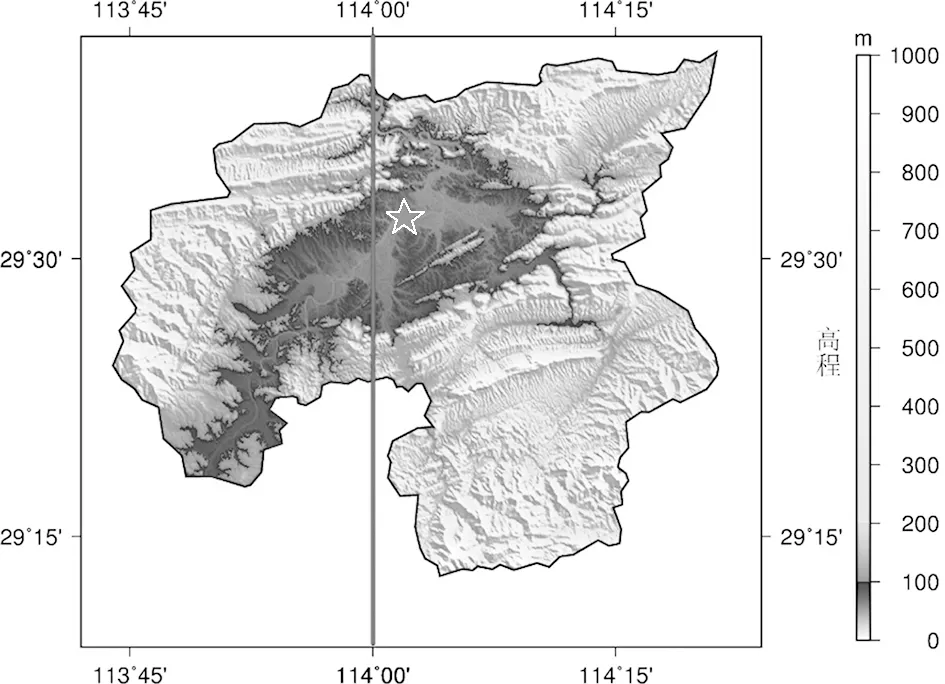
图1 崇阳县地形分布图，红色五角星为县城所在位置

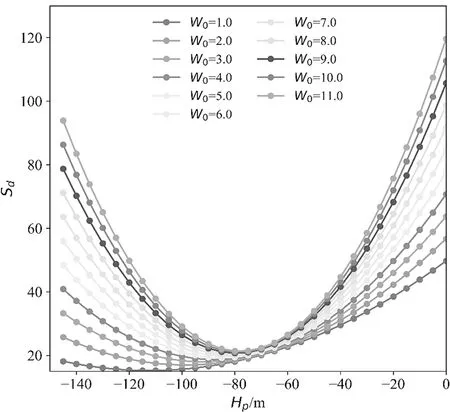
图2 设置不同高程抵偿面Hp及W0值时，每公里长度投影变形加权平方和Sd的变化示意图

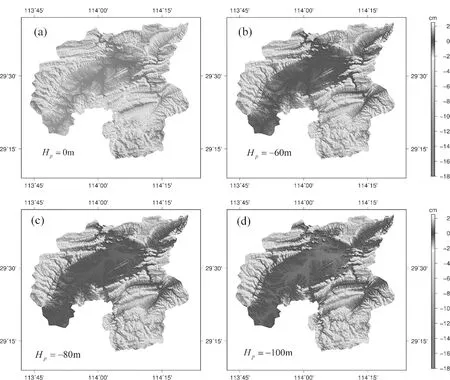
图3分别采用0m(a)、-60m(b)、-80m(c)和-100m(d)高程抵偿面时，崇阳县每公里长度投影变形分布图

由图3可以看到，高程抵偿面在-100 m～-60 m范围变化时，满足投影变形要求的区域面积变化并不大，主要差异在于满足投影变形要求的区域中，长度投影变形值的大小略有变化。当高程抵偿面为 -80 m时，满足投影变形要求的区域范围内平均投影变形最小，大部分地区接近于0。因此如采用具有高程抵偿面的方案，则最优高程抵偿面为 -80 m。如果从使用方便性上来考虑，由图3(a)(不施加高程抵偿)和图3(c)的比较来看，满足投影变形要求的区域面积差别并不是太大，且不施加高程抵偿面时大部分地区每公里长度投影变形也小于 5 cm，因此无高程抵偿面方案也较为实用。

4.2 武汉市投影变形分析

武汉市地理位置范围为东经113°41′～115°05′，北纬29°58′～31°22′，东西跨度最大横距为 134 km，南北最大纵距为 155 km，如图4所示。地形属残丘性河湖冲积平原，中间地平，南北丘陵、岗垄环抱，海拔 200 m以上的山地仅占全市面积的5%左右，中心城区海拔在 20 m左右。如采用国家统一3°带投影，取114°E(位于主城区西侧约 25 km)作为中央子午线，则东部较大部分地区每公里长度投影变形将超限[6]，且主城区内投影变形较大。

当使用式(4)和式(5)计算武汉市每公里长度投影变形值，仅根据PH设定权值，W0设为3，共采用高程点 1 161 959个，计算得到Sd的分布如图5所示，中央子午线的搜索间隔为5′，高程抵偿面的搜索间隔为 5 m。由图5可以看到，当中央子午线取为114°20′，高程抵偿面设为 0 m时，加权每公里长度投影变形残差平方和最小，这一结果与当前武汉2000坐标系所选用的高斯投影中央子午线和抵偿高程面是一致的。图6(a)中反映了当中央子午线取为114°20′，高程抵偿面设为 0 m时，武汉市地面点每公里长度投影变形分布图，可见每公里长度投影变形值最小处并不在中央子午线附近，而是分布其两侧，且与高程抵偿面选为平均高程面投影变形最小值位于中央子午线附近的方案相比，此方案投影变形较小的区域分布更广，这是由于高程归化影响与高斯投影变形的影响具有相互抵偿作用。因此虽然武汉市平均高程为 20 m左右，但高程抵偿面取 -20 m(即将投影面抬高 20 m，图6b)时，结果并不是最优。因此武汉市最优平面独立坐标系的建议方案为：中央子午线经度为114°20′，无高程抵偿。

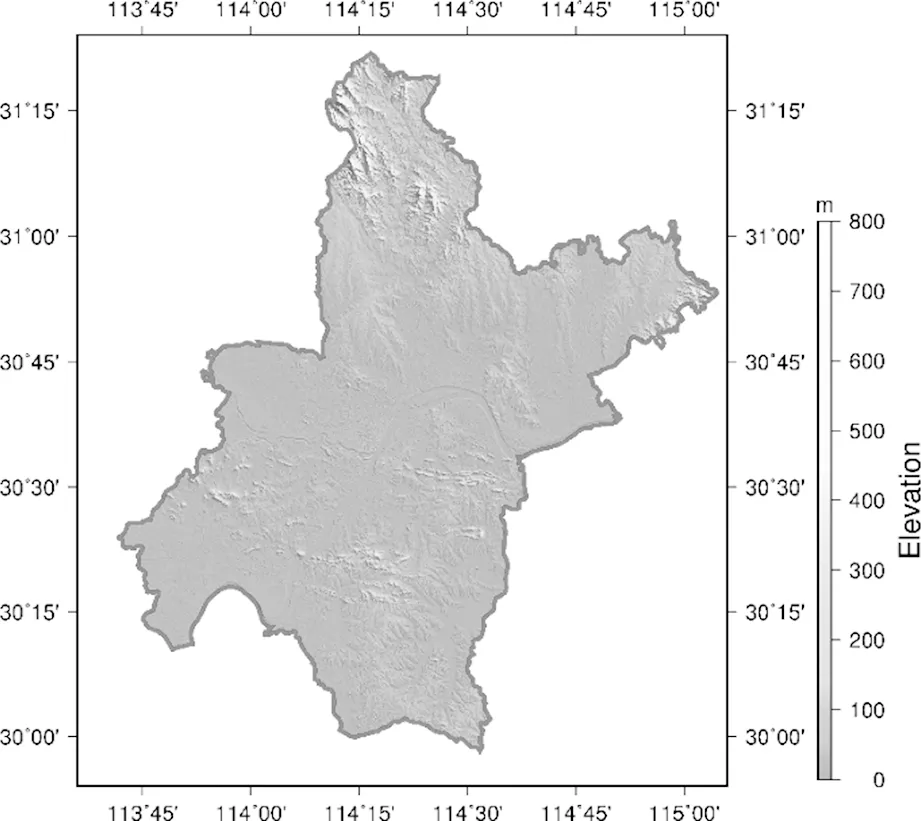
图4 武汉市地形分布图

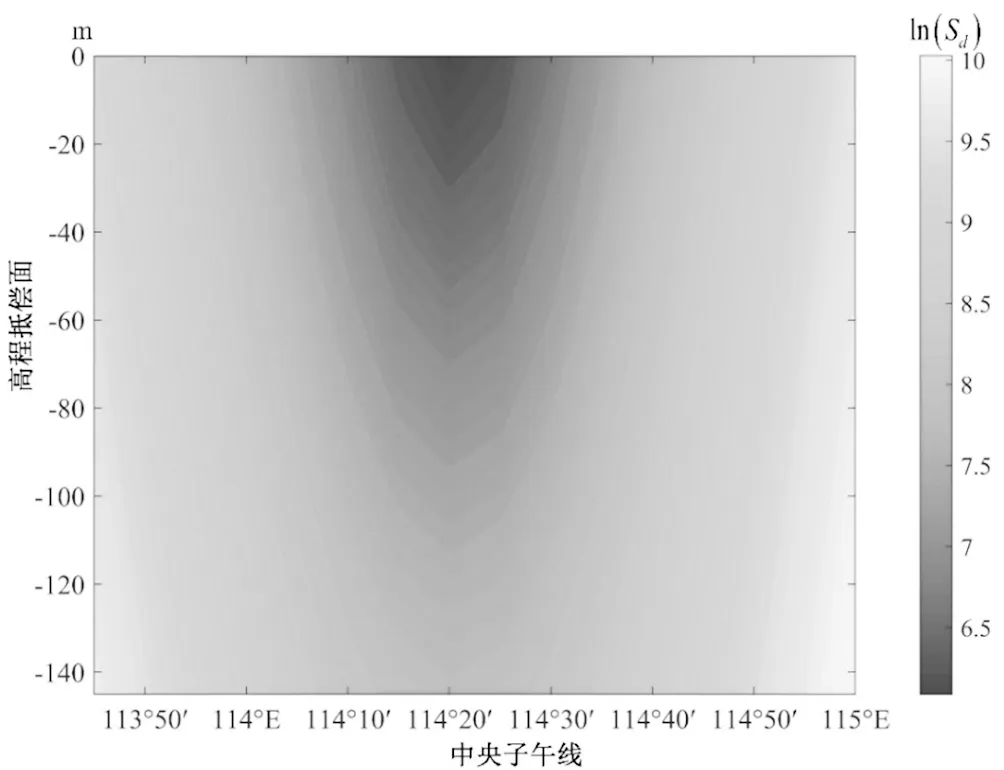
图5 采用不同中央子午线及高程抵偿面，基于SRTM数据计算得到的加权每公里长度投影变形之和Sd分布图

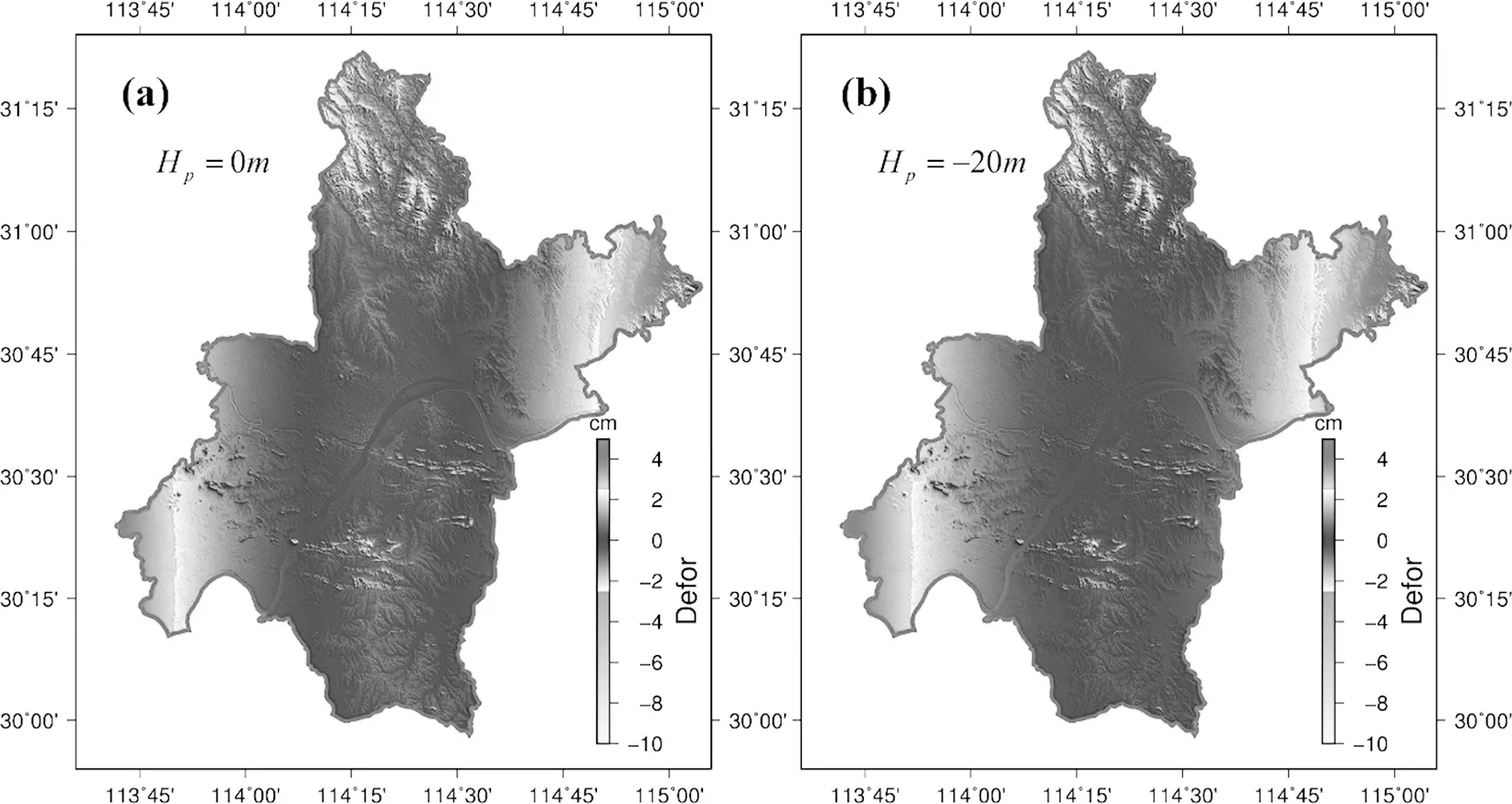
图6采用114°20′中央子午线，高程抵偿面分别设为0m，-20m时，武汉市地面点每公里长度投影变形分布图

5 结 论

本文提出了一种基于高分辨率DEM数据建立区域平面独立坐标系的方法，该方法可充分考虑地形影响及区域建设发展的需要。基于高分辨率DEM数据可获取整个区域的每公里长度投影变形值分布，从而制定具有针对性的基于CGCS2000的平面直角坐标系建立方案。本文将该方法应用于崇阳县及武汉市的城市平面独立坐标系分析中。结果显示对于崇阳县，采用114°E作为中央子午线，如采用具有高程抵偿面的方案，则最优高程抵偿面为 -80 m(即将投影面抬高 80 m)，但从使用方便的角度出发，无高程抵偿的方案也较为实用。对于武汉市，最优独立平面坐标系建立方案为：中央子午线设为114°20′，无高程抵偿，与当前使用的武汉2000坐标系一致。