气动肌肉机械腿摆动动力学建模与控制

黄继清,金英连,陈迪剑,王斌锐

(中国计量大学 机电工程学院,浙江 杭州 310018)

腿足式机器人适应自然界的非结构化环境,具有多地形适应能力。研究发现,机械腿建模与关节力矩控制是腿足式机器人研究的重点。在Raibert M[1]对机械腿研究基础上,波士顿动力公司研制出的军用BigDog[2]可以胜任多地形的运输任务,吸引一大批学者参与到腿足式机器人的研究中。意大利理工学院的Focchi M[3]在液压四足HyQ上实现了‘V’字形斜坡上的行走。Semini C[4]在HyQ基础上设计了液压、力矩驱动的HyQ2Max,增加了负载能力,赋予更灵活的运动能力。国防科技大学张太辉[5]对液压四足机器人机械腿关节计算力矩控制进行研究,再现关节位置控制下的关节力矩。麻省理工学院Seok S[6]团队设计的MIT Cheetah,使用本体感知的(proprioceptive)、高扭矩密度的直驱永磁同步电机驱动,具有反向驱动能力(backdrivability),降低触地碰撞力。使用力矩控制的关节,可以提高机器人的运动能力。

相比以上机械腿,气动肌肉机械腿结构简单,质量轻,类似动物的肌肉-骨骼系统[7]。美国凯斯西储大学Hunt A[8]在气动肌肉四足Puppy上训练神经网络控制器,在跑步机上完成了后腿行走实验。韩国Kaneko T[9]控制气动肌肉双足机器人的足底力,实现了双足的弹跳运动。日本的东京工业大学[10]、大阪大学[11]和东京大学[12]的气动肌肉足式机器人在仿生机构上取得进展,均无关节力矩控制方面的研究。由于气动肌肉驱动的关节力矩难以测量与控制,力矩控制在气动肌肉四足机器人中的应用文献不多,在外骨骼机器人中存在关节力矩控制研究[13]。

参考文献[14]关节自由度配置,本文设计一种气动肌肉驱动的两自由度机械腿,建立关节驱动机构模型和关节力矩模型;在位置控制器输出中加入机械腿动力学计算力矩项,设计拮抗气动肌肉拉力控制器和关节位置控制器;在仿真和实验中,对机械腿摆动时的关节位置跟踪控制进行研究。

1 机械腿建模

1.1 驱动机构模型

机械腿由躯干、大腿和小腿组成,关节驱动机构模型如图1。髋关节采用链轮传动,半径r,mm,转动中心O;膝关节采用四连杆结构,如图1中粗线所示。θh和θk分别表示髋关节和膝关节角度,rad;Pi表示气动肌肉,下标i=u,d,l,r,表示不同安装位置;Fi表示气动肌肉拉力,N;xi表示气动肌肉末端位移,mm。

图1 机械腿关节驱动机构模型Figure 1 Joints drive mechanism model for mechanical leg

设计髋关节角度活动范围[θh_min,θh_max],则气动肌肉位移:

xu=r(θh_max+θh);

(1)

xd=r(θh_min-θh)。

(2)

膝关节示如图2所示,现在推导膝关节角度θk与气动肌肉Pl位移xl的关系。膝关节角度θk=π-γ-θ2,其中γ定义为直线HA的延长线AO1与直线DE夹角,交点O1。在△AEO1中,γ=θ1-ε1,其中θ1和ε1分别根据四边形AEGH和△ADE的边长关系求得。θ2=β-ε3-φ+λ2,ε3为△ADE的内角,λ2已知,需要在△BCD和△ABD中根据余弦定理求β和φ。α=π+λ1-θ1-ε2,λ1已知,ε2=π-ε1-ε3,则在△ABD中,利用余弦定理可求出直线BD长度LBD,现在△BCD和△ABD边长都为已知,β和φ即可求解。

图2 膝关节示意图[15]Figure 2 Schematic diagram of knee joint

膝关节角度θk与气动肌肉Pl位移xl的关系为

θk=fl(xl)=π+ε1+ε3-λ2-

(3)

式(3)中:L表示图2中线段长度,mm。根据腿足末端空间的要求,综合设计机械腿髋关节角度活动范围为[-0.43,1.13],膝关节目标转角范围为[0,2.44],大腿长度0.4 m,小腿长度0.355 m,则可具体设计膝关节驱动机构参数数值,见表1。将表1中的数值代入式(3),求其反函数可得

(4)

在图2中,膝关节角度还可以表示成θk=π-θ4+γ1,同理膝关节角度θk与气动肌肉Pr位移xr的关系可表示成

(5)

根据表1的参数数值,同样可以求得式(5)的反函数

(6)

表1 膝关节驱动机构参数

1.2 关节力矩模型

如图1髋关节部分所示,髋关节主动力矩可表示成

τh=τu-τd=(Fu-Fd)r。

(7)

式(7)中:τh为拮抗气动肌肉Pu和Pd对髋关节产生的合力矩,N·m;τu和τd分别表示气动肌肉Pu和Pd的拉力Fu和Fd在力臂r下对O点施加的力矩,N·m。

本文设计髋关节力矩到气动肌肉拉力的映射关系为:

(8)

(9)

式(8)、(9)中:τu和τd的初始力矩都为τh0,N·m;τh0>0可保证拮抗气动肌肉在任意时刻都保持在伸直状态。

膝关节主动力矩分析如图2,τl和τr分别是拉力Fl和Fr对点A和B施加的力矩,N·m。△ADE和△BCF分别在τl和τr作用下绕点A和B转动,分别在杆3的反作用力Fdl和Fdr作用下平衡,N,作用点分别为D和C。则△ADE和△BCF静力学平衡方程分别为：

τl=Fldl=Fdlldl;

(10)

τr=Frdr=Fdrldr。

(11)

式(10)、(11)中,dl和ldl分别为Fl和Fdl对A点的力臂,m;dr和ldr分别为Fr和Fdr对B点的力臂,m。力臂可分别在△AEG、△ACD、△BFJ和△BCD中根据几何图形三角函数关系求解,根据式(4)、(6),可表示成以膝关节角度θk为变量的函数关系。

假设四连杆ABCD质量可以忽略,则杆3为二力杆,Fdl和Fdr大小相等,方向相反,且沿着杆3方向,则有力矩比例系数

(12)

小腿绕四连杆瞬心转动的主动力矩

τk=k(τl-τrctau)=k(Fldl-Frdrctau)。

(13)

式(13)中:τk为膝关节主动力矩,N·m;k为比例系数,k>0。

在四连杆处于静力学平衡条件下,k=1。本文设计膝关节力矩到气动肌肉拉力的映射关系为:

(14)

(15)

式(14)、(15)中:τk0为τl和τr的初始力矩,N·m,τk0>0。

1.3 动力学模型

将机械腿简化成典型的二连杆模型,躯干为基座。选用拉格朗日动力学方法,建立机械腿动力学模型如下:

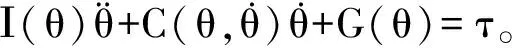
(16)

式(16)中:θ是关节角度矢量,θ=[θhθk]T;I为惯性矩阵,I∈R2×2;C为离心力和科氏力矩阵,C∈R2×2;G是重力距矢量,G=[G1G2]T;τ是关节主动力矩矢量,τ=[τhτk]T。

矩阵I、C和矢量G的元素如表2所示。g为重力加速度;m1和m2分别是大腿和小腿的质量,kg;lm1和lm2分别为大腿和小腿的质心距,m;Lul和Lll分别为大腿和小腿的长度,m;I1和I2分别为大腿和小腿的转动惯量,kg·m2。

表2 机械腿动力学矩阵及矢量元素

Table 2 Elements of matrix and vector in dynamics of mechanical leg

元素内容I11m1l2m1+m2(L2ul+l2m2+2Lullm2cos(θk))+I1+I2I12m2(l2m2+Lullm2cos(θk))+I2I21m2(l2m2+Lullm2cos(θk))+I2I22m2l2m2+I2C11- θkm2Lullm2sin(θk)C12-( θh+ θk)m2Lullm2sin(θk)C21 θhm2Lullm2sin(θk)C220G1gm1lm1sin(θh)+gm2Lulsin(θh)+gm2lm2sin(θh+θk)G2gm2lm2sin(θh+θk)

2 控制器设计和系统仿真

2.1 控制器设计

设计式(16)中力矩

(17)

式(17)中:v是待设计的控制律。则整个机械腿动力学如下:

(18)

式(18)可化简为

(19)

由式(18)可见,机械腿动力学解耦成一个线性定常系统。若给定机械腿关节角度为θr,θr二阶可微,则可设计控制律

(20)

式(20)中:Kv和KP就是比例-积分控制器系数。联立式(19)、(20),误差动力学方程为

(21)

式(21)中:e为关节角度跟踪误差,e=θr-θ。根据李雅普诺夫稳定性定义,适当选择参数Kv和KP,误差动力学渐近稳定。

联立式(17)、(20),有

(22)

设计机械腿摆动控制双闭环策略,控制框图如图3所示。单腿关节映射模型,一部分由式(1)、(2)、(4)和(8)组成,用来计算气动肌肉实际位移x,mm;一部分由式(8)、(9)、(14)和(15)组成,用来计算气动肌肉给定拉力Fg,N。拉力控制器输出电压u控制调压比例阀,V。

图3 机械腿摆动控制框图Figure 3 Block diagram of control of swinging mechanical leg

气动肌肉拉力采用前馈反馈[16]控制策略。拉力控制器由气动肌肉逆模型前馈控制器和PI(Proportional Integral)误差补偿控制器并联形成。参考文献[17],将气动肌肉收缩力模型等效成弹簧单元和收缩单元并联输出力模型

Fi(xi,pi)=Fci(pi)-Ki(pi)xi。

(23)

式(23)中:p表示气动肌肉相对气压,MPa;Fc表示收缩单元收缩力,N;K表示弹簧单元刚度,N/mm。在0～0.6 MPa压力下,Fc和K为

(24)

式(24)中:c,v和pd为气动肌肉拟合模型参数,单位分别为N,N/mm和MPa。

由式(23)、(24),设计两个中间变量

(25)

(26)

式(26)中:p1i和p2i为气压变量,MPa。则气动肌肉逆模型前馈控制器输出如下:

pfi=p1if(p1i)+p2if(p2i)。

(27)

式(27)中:pfi为前馈控制器输出,MPa;

PI误差补偿控制器表达形式如下:

(28)

式(28)中,pci为PI控制器输出,MPa;ei(t)=Fgi-Fi,为气动肌肉给定拉力和测量拉力之间的偏差,Kpi和Kii分别为比例-积分系数。

调压比例阀气压转电压的线性系数为kpu,则拉力控制器输出

ui=kpu(pfi+pci)。

(29)

2.2 仿 真

在Matlab中,利用Simulink中的s函数编写机械腿摆动控制系统。机械腿物理参数如表3。

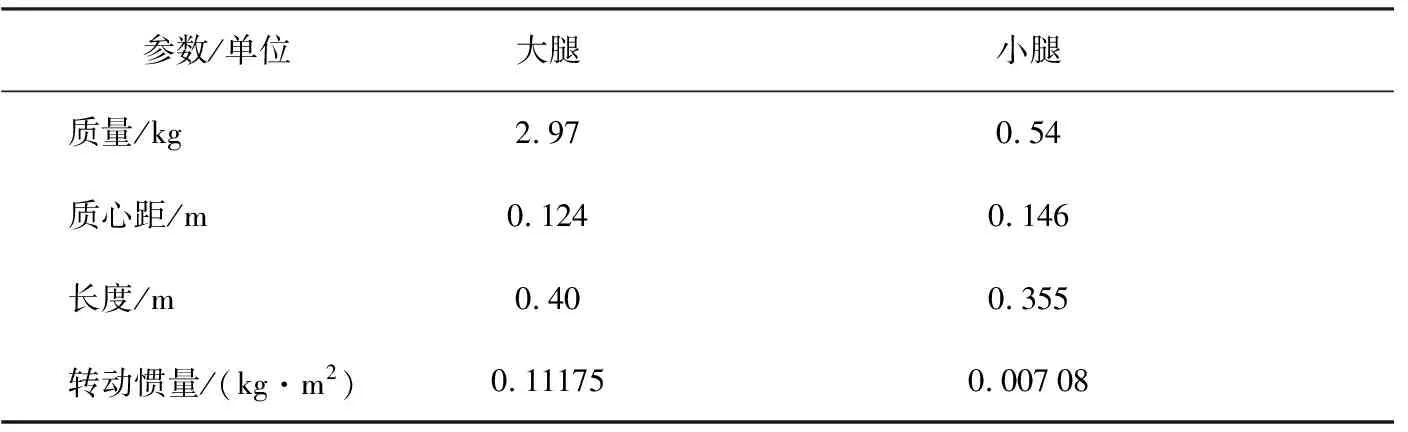
表3 机械腿物理参数

图4 仿真中关节角度及力跟踪曲线Figure 4 Joints angle and force tracking curves in simulation

在0～2.5 s内,系统根据给定的初始力矩,计算与调整四根气动肌肉的初始拉力和气压,存在明显的抖动现象,原因是仿真刚开始,机械腿关节角度跟踪误差和关节力矩跟踪误差较大,比例控制控制系统出现超调和振荡。2.5 s以后,关节力矩和气动肌肉拉力跟踪渐渐稳定,关节角度实现了稳定的正弦波跟踪效果。髋关节克服整条腿重力的力矩由气动肌肉拉力Fd提供,Fd跟踪曲线基本与角度变化趋势一致。气动肌肉Pu在初始力矩的设置下,拉力Fu保持在2N附近。在拮抗气动肌肉拉力Fd的约束下,拉力Fu产生周期性波动,波动幅值2N,变化趋势基本于气动肌肉拉力Fd保持相同。膝关节角度和记录跟踪曲线分析于髋关节基本相同,膝关节气动肌肉Pr的给定拉力Frr并不像髋关节气动肌肉给定拉力Fur是常值,因为拉力Fr对膝关节的作用力臂dr是随着膝关节角度变化的,同时在图4(d)中,膝关节力矩曲线穿过0 N·m,由式(15)可知,气动肌肉拉力Fr在零点连续,但是导数并不存在,因此拉力Fr会出现突变和尖刺。髋、膝关节角度跟踪误差在±1°内,角度跟踪误差均方根分别是0.75°和0.67°,力矩跟踪误差在±0.3 N·m以内。关节角度仿真曲线的跟踪效果初步验证了动力学控制的有效性,机械腿摆动控制系统正弦跟踪性能良好。

3 实 验

机械腿实验平台实物如图5。气动调压比例阀为ITV2050-212N(SMC)型号,在设置成最大增益条件下,幅值0.6 MPa的阶跃响应时间约为300 ms。实验采用自制气动肌肉,直径20 mm。调压比例阀和气动肌肉整体气压测试响应频率10 Hz以内。拉力传感器型号为ZNLBM-100 kg型号,线性度0.1%全量程,拉力响应频率不超过10 Hz,输出模拟信号0～5 V。角度编码器为CHA38S6单圈绝对式编码器,分辨率12位。IO模块为EL3068(BeckHoff)模拟电压输入端子和EL4008模拟电压输出端子,电压量程0～10 V,分辨率12位,分别用来控制调压比例阀气压和读取拉力传感器变送器输出电压。嵌入式控制器为CX2040(BeckHoff)型号,搭载WES7系统。应用程序开发软件TwinCAT3和EtherCAT通信协议实现了运动实时控制功能。

设置关节位置环控制程序运行周期10 ms,气动肌肉拉力环控制周期5 ms。髋、膝关节初始角度分别为-30°和60°,给定角度输入信号均为正弦周期信号,幅值15°,周期5 s。为减少拉力控制器的数量,设置气动肌肉气压pu和pr始终为0.13 MPa和0.15 MPa,气动肌肉Pu和Pr始终处于被动拉伸状态。设置气动肌肉气压pd和pl初始气压分别为0.02 MPa和0.15 MPa。拉力传感器可以实时测量被动气动肌肉拉力Fu和Fr,通过控制气动肌肉拉力Fd和Fl,补偿被动气动肌肉拉力对关节产生的力矩。实验通过对气动肌肉拉力的闭环控制和力臂的实时解算,实施关节力矩控制实验。机械腿摆动实验结果如图6。

图5 机械腿实验平台Figure 5 Experiment setup of mechanical leg

图6 实验中关节角度及力跟踪曲线Figure 6 Joints angle and force tracking curves in experiment

实验开始时,髋、膝关节稳定在初始角度,后在正弦信号的作用下,关节开始转动。由关节角度跟踪曲线可知,机械腿重力力矩越接近最大值时,即对应髋、膝关节角度分别为-50°和90°时,角度跟踪误差逐渐变大,是因为实际系统的非线性程度在不断增大。髋、膝关节力矩跟踪误差在±1.5 N·m以内。给定髋关节力矩曲线还出现较大尖峰,是因为气动肌肉拉力Fd跟踪误差最大40 N,经过负反馈控制,动力学计算力矩出现突变,导致关节给定力矩出现较大的尖峰。髋、膝关节的力矩跟踪曲线误差较大,力矩跟踪效果没有仿真理想,主要是因为存在建模误差：一方面是实验的逆动力学模型的简化,机械腿物理参数值的选取与实际机械腿物理参数有偏差;另一方面是实验中拉力传感器带宽小,实际气动肌肉拉力和气压关系存在迟滞,力矩跟踪的响应速度慢,跟踪曲线出现滞后现象。实际的系统还由一系列的干扰因素。髋关节气动肌肉Pu和Pr在拮抗气动肌肉中成被动工作状态,因此在图6(e)和(f)中,拉力Fu和Fr曲线变化趋势分别与主动拉力Fd和Fl曲线变化趋势一致。髋、膝关节角度跟踪误差在±3°以内,从关节空间映射到足端空间,误差可接受。

为了进一步验证本文动力学控制效果,评估气动肌肉机械腿关节跟踪性能,在图6中,选择前两个完整摆动周期,计算关节角度最大跟踪误差和跟踪误差的均方根,与文献[13]中的下肢康复机器人关节角度跟踪控制结果对比,见表4。本文髋、膝关节的角度跟踪误差均方根都小于文献,说明本文关节角度跟踪精度和性能优于文献,机械腿关节实现摆动相平稳的正弦跟踪控制。

表4 关节角度跟踪误差比较

4 结 论

建立了机械腿的摆动动力学模型,使用计算力矩控制方法对机械腿关节进行位置跟踪控制,仿真和实验结果表明:

1)拉力控制器的设计,可实现气动肌肉在不同末端位移条件下的拉力跟随控制;

2)对四连杆膝关节主动力矩的分析,可解决膝关节力矩如何映射到气动肌肉拉力的问题,实现四连杆传动的膝关节力矩控制;

3)建立拮抗气动肌肉关节建模,可实现关节力矩的检测与控制,计算力矩控制可应用在自主设计的气动肌肉机械腿摆动运动控制中。

下一步的工作需要利用关节力矩控制,对机械腿在地面任意高度的弹跳控制进行研究。