数字全息光学实验探究及再现清晰度优化

黄威龙，白 欣，梁海坤，梁绮霞，曾育锋,b

(华南师范大学 a.物理与电信工程学院; b.物理国家级实验教学示范中心，广东 广州 510006)

全息光学的概念是由Gabor于1948年首次提出，其基本思想是通过光波干涉的方法，同时记录光波的振幅和相位信息. 而数字全息则是利用高精度的CCD或COMS相机和空间光调制器[1](SLM)进行采集和再现，由于降低了对环境的要求，免去冲洗的麻烦，同时可以对数据进行二次开发，如滤波、存储、传输、加密安全等，拓展了全息的应用领域，使得近年来关于数字全息[2]的研究越来越广泛. 本文利用数字全息光学平台[3]对数字记录、数字再现、光学记录等实验进行研究.

1 实验原理

1.1 数字全息记录及再现

数字全息记录是利用数字相机代替全息干板记录全息图，若想获得高质量的数字全息图、完好地重现物波，则需要满足奈奎斯特[4]采样定理，即记录介质的空间频率必须是全息图表面上光波空间频率的2倍以上. 因此，全息图表面上光波的最大空间频率为

(1)

只要满足奈奎斯特定理，参照光[5]可以是任何形式，可以是准直光也可以是发散光，可以垂直入射数字相机，也可以一定角度入射相机.

如图1所示，物体位于xoy平面上与全息平面xHoHyH相距d，即全息记录距离，物体的复振幅[6]分布为u(x,y). 数字相机位于xHoHyH面上，iH(xH,yH)是物光和参照光在全息平面上的干涉光强分布.x′o′y′面是数字重现的成像平面，与全息平面相距d′，也称再现距离.u(x′,y′)是重现像的复振幅分布，是二维复数矩阵，可以同时得到再现像的强度和相位分布. 对于图1中的坐标关系，根据菲涅耳衍射[7]公式可以得到物光波在全息平面上的衍射光波场分布O(xH,yH)为

(2)

图1 数字全息记录和再现结构及坐标系示意图

其中λ为波长，k=2π/λ为波数. 全息面上，设参考光波的分布为R(xH,yH),则全息平面的光强分布iH(xH,yH)为

iH(xH,yH)= [O(xH,yH)+R(xH,yH)]·

[O(xH,yH)+R(xH,yH)]*.

(3)

在满足菲涅耳衍射条件，重现距离为d′时，成像平面上的光场分布u(x′,y′)为

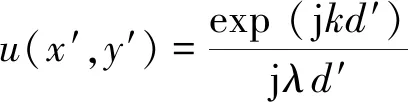
(4)

将(4)式中的二次相位因子(x-xH)2+(y-yH)2展开，则可以写成

(5)

在数字全息中，为了获得清晰的重现像[8]，必须d′=d，当d′=-d时，重现像的复振幅分布为

(6)

这样，利用傅里叶变换可以求出重现像. 其中，傅里叶变换[9]的频率为

(7)

(8)

根据频域采样间隔和空域采样间隔之间关系可得

(9)

(10)

其中，M和N分别为2个方向的采样点个数. 则全息平面的像素大小和重现像面的像素大小之间的关系为

(11)

(12)

(11)式和(12)式表明，重现像的像素大小和重现距离d成正比，重现距离越大，Δx′和Δy′就越大，空间分辨率就越低.

1.2 光学全息记录及数字全息再现

反射全息法是将物光和参考光从高精度的CCD摄相机两侧入射，从而利用CCD摄相机记录物体全息图[10]的方法. 利用搭建的光路，可以记录获得物体的相位和振幅信息，从而获得强度等信息.

如图2所示，首先激光器发射出为632.8 nm激光，通过偏振片调节激光的透过率[11]，随后通过空间滤波器进行滤波，使用准直镜校准，最后利用光阑[12]调节光束的大小，进入分光棱镜A后分成2束光，一束光通过反光镜1进入分光棱镜B，另外一束光通过反光镜2及反光镜3反射后照射到物体上，物体反射的光进入分光棱镜B，2束进入分光棱镜B的光发生干涉，随后进入CCD/COMS相机中，记录下光波的信息.

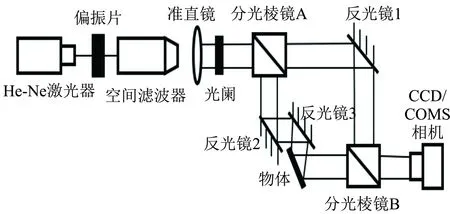
图2 光学全息记录光路图

图2中元器件相关技术参量如下：He-Ne激光源λ=632.8 nm，准直镜d=150 mm，COMS相机μ=5.2 μm.

1.3 HRO数字相减法消除零级光斑原理

设全息记录平面上的物光和参照光的复振幅分别为O(x,y)和R(x,y)，则全息记录平面的光强分布为

IH(x,y)= |O(x,y)|2+|R(x,y)|2+

O(x,y)R*(x,y)+O*(x,y)R(x,y).

(13)

可见，全息再现的光强分布与(13)式成正比，第1项与第2项构成零级光，第3项为原始像，第4项为共轭像. HRO相减是指用全息图中记录的所有光减去上述参考光强度|R(x,y)|2以及物光波强度|O(x,y)|2. 因此，最后得到的HRO数字相减全息图光波强度为

IH′=+O(x,y)R*(x,y)+O*(x,y)R(x,y).

(14)

根据(14)式可知， 进行HRO数字相减法处理后，只能得到原始像与共轭像. 因此可以消除零级光斑的影响.

1.4 Sobel算子处理法

采用Sobel算子[12]对数字全息图I(x′,y′)进行预处理，随后进行傅里叶变换，得到Sobel算子处理后的数字全息图的频谱为

I(ξ,η)= |I(ξ,η)-I(ξ,η)exp (j2πΔξ)|+

|I(ξ,η)-I(ξ,η)exp (j2πΔη)|,

(15)

以ξ轴方向为例进行分析.

Iξ(ξ,η)= |I(ξ,η)-I(ξ,η)exp (j2πΔξ)|=

I(ξ,η)|1-exp (j2πΔξ)|=

I(ξ,η){[1-cos (2πΔξ)]2+

[sin (2πΔξ)]2}1/2=

I(ξ,η)[2-2cos (2πΔξ)]1/2.

(16)

由(16)式可知，在Δξ=0附近，频谱面上零级光对应的区域趋近于0. 其中|exp (j2πΔξ)|对数字全息图的影响如图3所示. 图3中，虚线三角形和正方形分别表示零级光和原始像、共轭像对应的频谱，实线表示Sobel算子作用后的这三项的频谱. 分析可知，Sobel算子对全息图的处理效果等效于在全息图频谱上加了带通滤波器. 这样，既可以滤除零级光的频谱，又能保留并增强原始像和共轭像的频谱值.

图3 Sobel算子在频域ξ轴方向对全息图的作用

1.5 Laplace算子处理法

采用Laplace算子[13]对数字全息图I(x,y)同时进行Laplace运算和卷积运算得

I(x,y)=-2I(x,y)⊗|rect|x/a|exp (-j2πβx)|,

(17)

式中，I(x,y)表示Laplace算子处理后全息图的强度分布，⊗表示卷积运算，α和β是待定常数，对应于原始像频谱的分布宽度和中心位置，2为Laplace算符

(18)

对(18)式进行傅里叶变换化简得

F[I(x,y)]=4π2(ξ2+η2)αsinc [α(ξ-β)]i(ξ,η)

以ξ轴方向为例，绘出一维图，如图4所示. 图中虚线三角形分别表示零级光和原始像、共轭像对应的频谱，实线表示Laplace算子作用后的频谱，用Laplace算子处理全息图等效于在全息图上叠加一个频谱滤波器. 这样，即滤掉零级光的频谱，降低共轭像的频谱值，有增强原始像的频谱值，使得再现图像的质量显著提高.

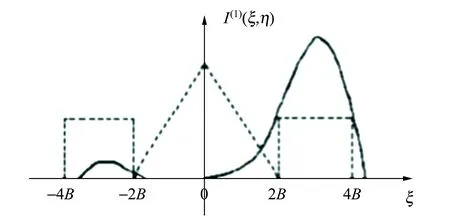
图4 Laplace算子在频域ξ轴方向对全息图的作用

2 实验结果与讨论

2.1 数字全息记录与再现

数字全息实验中，选择了图5(a)作为样品1，经过数字全息光学系统获得样品1的全息图如图5(b)所示[图5(b)为放大2 000倍的部分图像].

(a)原始图 (b)部分全息图图5 样品1及部分全息图

(a)未处理 (b)数字处理图6 样品1再现图

随后通过全息系统进行数字再现，获得样品1的再现图[图6(a)]，由于[图6(a)]的零级亮斑较强，成像质量不高，因此，采用HRO数字相减方法处理全息图，获得清晰的样品图案([图6(b)]). 经过HRO数学相减法对零级光斑进行消除后会出现清晰较高的再现图案.

2.2 光学全息记录与数字全息再现

在光学全息实验中，采用2015版一元硬币[图7(a)]作为样品，利用硬币上的元字进行反射全息实验. 搭建光路平台，将参照光及物光干涉后的信息记录进高精度CCD摄像机中，随后将信息输入计算机之中，生成全息图并反色获得[图7(b)].

(a)原始图 (b)反色全息图7 样品2及反色全息图

采用数字全息系统对全息图进行数字再现后，获得图如图8(a)所示. 实验结果显示，再现图中会出现多个像，分布在整个再现图像上，并且图像记录清晰度不高. 因此，对光路中反射镜角度进行微调，同时将再现光距离由原来180 mm调节至200 mm，修改参照光光强后可以获得较为清晰的再现图像[图8(b)]，达到光学再现的效果.

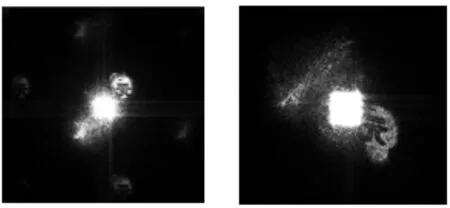
(a) (b)图8 样品2的再现图

在达到光学再现的效果之后，利Matlab对全息图进行Sobel算子处理，并进行再现获得图如图9(a)所示 .

从再现的图像来看，经过Sobel处理后的图像明显清晰于未处理的图像，原因在于经过Sobel处理后，图像的中心零级光光强降低，使得原始像可以显示.

另外，还利用Matlab将原来的全息图进行Laplace算法处理，再现后获得如图9(b)所示的再现图.

由图9(b)可以看出，该图的图像质量也明显高于原来的未进行任何处理的全息图. 在此基础上对原来的全息图先进行了Sobel算法处理，再进行Laplace算法处理，随后再现出图像如图9(c)所示.

(a)Sobel处理 (b)Laplace处理

(c)Sobel处理品再Laplace处理图9 数字再现图

由图9(c)可以看出，不仅是所再现的原始像变得更加清晰，该方法还可以使原始像的光强变得更高，可以更加得凸显出原始像的特征，有效地提高了再现的效果.

3 结束语

利用菲涅耳积分再现算法对数字记录以及光学记录所获得的全息图进行了再现，同时在实验中通过HRO数字相减法的使用，光路中反射镜角度的微调以及再现距离，再现光强度的修改，消除了零级光的影响，获得较为清晰的再现图，达到了数字记录数字再现以及光学记录数字再现的目的. 利用Matlab对光学记录的全息图进行Sobel算法以及Laplace算法的处理，同时也利用2者的组合，对全息图的图像进行优化，获得清晰的再现图，有效地提高了再现图像质量. 实现了后期利用计算机软件改进全息图图像质量获得清晰再现图的目的.