一种结合高斯统计的点云引导滤波算法

李广金，杨 涛

（1.西南科技大学 信息工程学院，绵阳 621010；2.特殊环境机器人技术四川省重点实验室，绵阳 621010）

0 引言

随着逆向工程和三维建模在制造行业的广泛应用，实物模型的三维点云成了主要操作对象[1～3]。由于三维信息采集设备固有的硬件误差和人为、环境等因素的干扰，测得的模型点云中不可避免含有部分噪声点，影响后续模型的重建精度和成像质量。因此，对采集到的模型点云进行去燥和平滑处理至关重要。

近年来，三维点云数据在噪声处理方面得到很大的发展。Digne[4]提出一种基于局部相似度的点云滤波去噪算法，通过平均曲率流将点云分解成低频和高频部分分别进行处理，但该方法依赖于局部点云的密度，不能很好的分辨成团的离群点和局部噪声点。Sergio等[5]提出一种基于增长神经气（Growing Neural Gas，GNG）网络的点云去噪和精简算法，对Kinect采集到的数据进行处理，能有效去除离群点，但对于点云模型缺少平滑处理。吴晓庆等[6]利用移动最小二乘法对点云进行平滑、重采样处理，虽然能有效平滑噪声点，但也会损失模型尖锐处几何特征。双边滤波算法由于具有良好的边缘保持特性，被大量用于点云噪声处理[7～9]，但其只能平滑局部噪声点，且算法耗时较长。

针对以上问题，本文提出一种结合高斯统计的点云引导滤波算法。在对点云数据进行KD-tree[10,11]拓扑连接后，首先采用高斯统计法去除点云离群点，然后通过点云引导滤波对剩余点云进行平滑处理。仿真实验展示了不同参数下高斯统计方法对离群点的去除效果，将点云引导滤波分别与均值滤波、双边滤波进行对比，验证了引导滤波算法的优越性。

1 离群点的去除

离群点是指那些偏离主体点云一定的距离、数量也比主体点云少很多的噪声点[12]。高斯统计去除离群点的算法思想如下：

定义di为某一已知点pi到其k个邻域点的平均距离，为di的均值，σ为di的标准差。

现假设di服从高斯分布，即，那么根据高斯函数曲线的特点，我们可以设定阈值：对于原始点云中某一点，当时，将其看作离群点从点云数据中去除，其中ε为人为设定的去噪参数。当ε=1时，根据高斯函数特点，理论上可滤除的点数量为原始点云的31.73%。

2 局部噪声点平滑

当距离主体点云一定距离的离群点被去除后，在局部点云表面仍有一些幅度比较小的噪声点不能被高斯统计的方法去除。这些噪声点会造成点云局部高低起伏，影响后续点云模型的重建精度，故需要对剩余点云进行平滑处理[13]。

2.1 点云引导滤波算法

引导滤波最初由何凯等[14]提出用于图像滤波，采用一张引导图计算线性模型系数，对输入图像进行滤波，使输出图像大体上与输入图像相同，纹理上却与引导图相似，具有良好的边缘保持特性和时间复杂度低的优势。根据三维点云的特点，可将引导滤波改进后应用到点云噪声平滑处理上[15]。

假设点云中某邻域平滑处理前后满足以下线性关系：

其中，p'ij为滤波平滑后的点，ai和bi为线性模型的待求参数，可通过求解式(5)在该邻域的极小值解出：

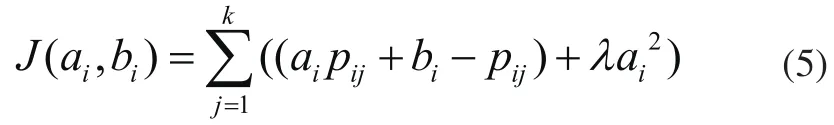
式中λ为控制平滑效果的人为设置参数。J（ai,bi)取极小值时，对ai和bi的偏导数为零。解得：

其中为此处邻域的几何中心：

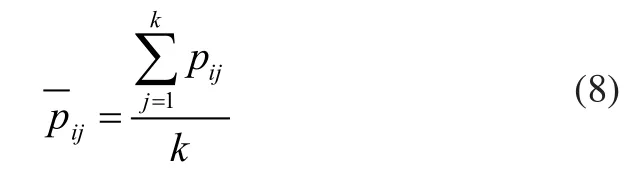
由于点云中任一点pi的邻域点集不完全相同，对应的ai和bi也不会相同，对点云中每一点重复以上计算，解出的ai和bi用于对该点作平滑处理：

从以上推导看出，通过将处理点的邻域点集作为引导窗口，使得平滑处理后模型能保持其邻域的几何特征。由式(6)、式(7)、式(9)可以看出，参数λ=0时，ai=1，bi=（0，0，0），输出点坐标等于输入点，点云局部噪声并未得到平滑；随着λ取值不断增大，ai相应减小，输出点越来越接近其邻域几何中心。实际应用中通常取λ＜1。

2.2 均值滤波算法

在图像处理领域，均值滤波是一种线性平均滤波器。在点云处理方面，均值滤波算法即为引导滤波参数λ趋于无穷大后的特殊情况。此时，平滑处理过程即为通过式(9)得到的邻域几何中心来代替处理点。

2.3 双边滤波算法

双边滤波平滑点云的表达式为：

此处Wc与Ws为高斯核函数：

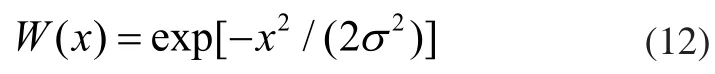
Wc为平滑函数，以该点到邻域点的距离为自变量。为平滑因子，其值越大，平滑效果越好，通常取为Wc自变量的最大值；Ws为几何特征保持函数，以此邻域法向量与该点到邻域点距离向量的內积作为自变量。为特征保持因子，其值越小，几何特征保持性能越好，通常取为Ws自变量的标准差。

双边滤波涉及点云法向量的相关计算，通常采用主元分析法[16]（Principal Component Analysis，PCA）对某局部点云法向量进行估计：

设ni为某邻域点法向量，则它与邻域点集满足关系：

定义矩阵Ci：

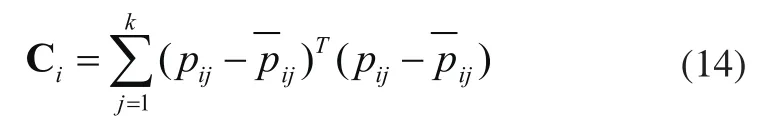
解出其最小特征值对应的特征向量即可作为ni的估计。

3 实验对比分析

采用3ds Max软件对汽车建模后，通过MeshLab软件对导出文件处理得到txt格式的三维数据点云，通过matlab R2016a软件对点云数据加入随机噪声点，依次采用前文介绍的算法编程进行处理。计算机硬件条件为：处理器Inter(R) Xeon(R) CPU E5-1603 v4 @ 2.80GHZ，内存8GB，显卡NVIDIA Quadro M2000。

3.1 离群点去除实验分析

由式(1)～式(3)可见，高斯统计去除离群点受邻域点数k和参数ε的影响。由图1(b)和图1(d)、图1(c)和图1(e)可看出，邻域大小相同时，ε取值越大，去除的离群点越少，这也符合高斯分布曲线特点。图1(d)、图1(e)、图1(f)可以看出，高斯统计阈值相同时，k取值越大，去除的离群点越少，因为邻域半径增大导致了模型表面附近的点被忽略了。对不同三维点数量的点云模型，µ和k取值对离群点去除效果都有影响。对车体点云取k=10，ε=1，去噪效果如图2所示。

图2 车体点云去除离群点

3.2 局部噪声点平滑实验分析

当模型点云中含有的离群点噪声被去除后，对比使用三种滤波算法平滑局部小型噪声点。取k=10，ε=1.96处理后的模型点云分别进行实验。

图3 轮毂点云局部噪声点平滑

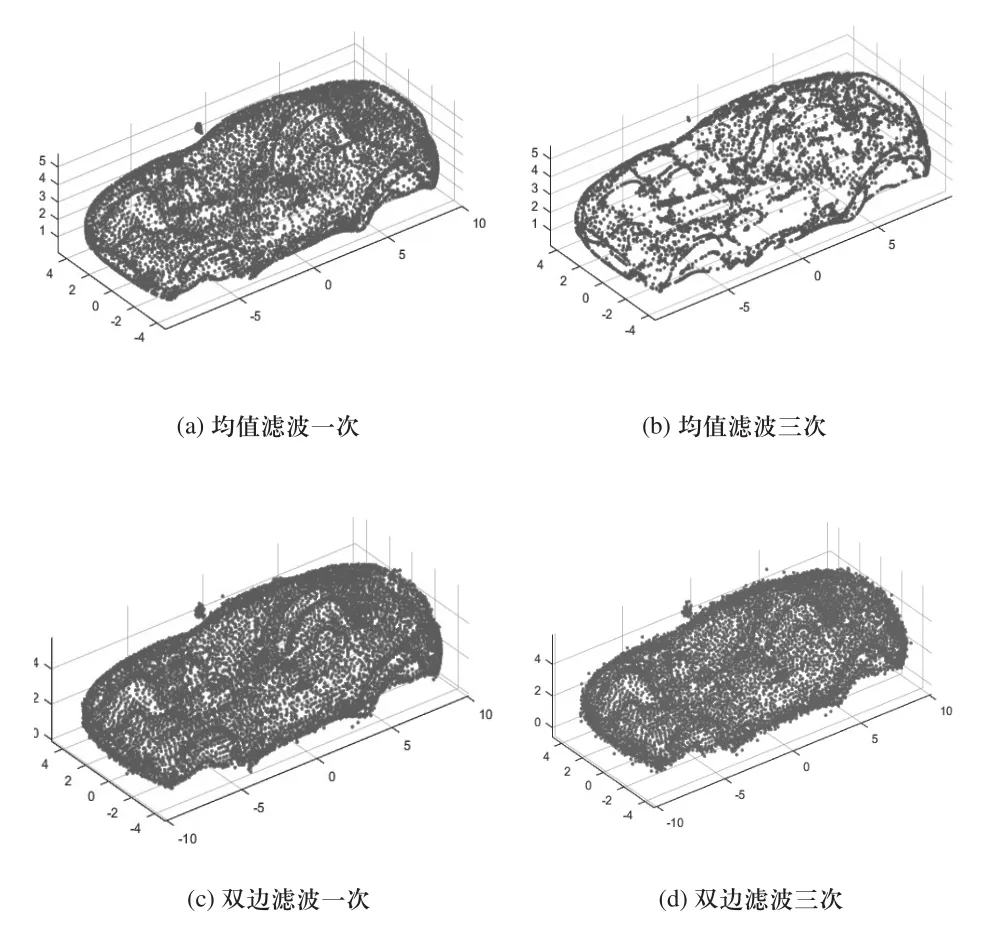
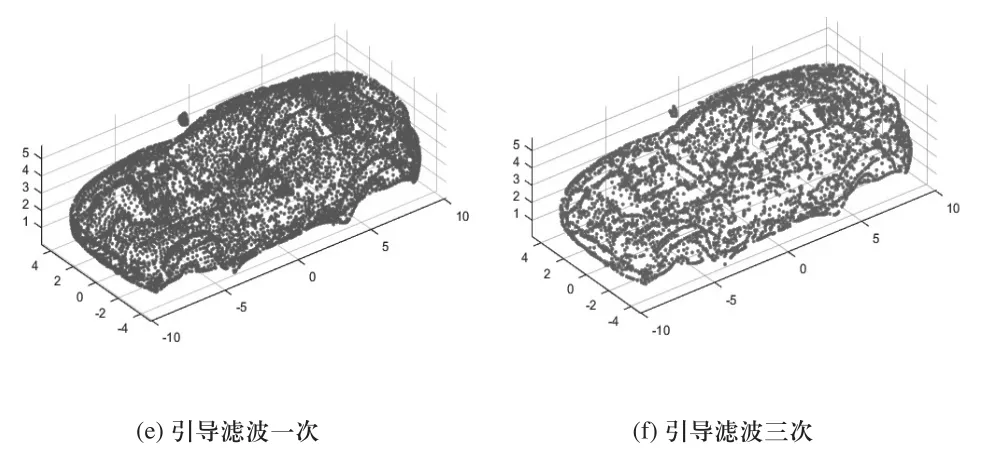
图4 车体点云局部噪声点平滑

图3(a)和图4(a)、图3(b)和图4(b)分别为均值滤波迭代一次和迭代三次的效果图，由于均值滤波通过选取邻域点集的几何中心点代替处理点，故随着迭代次数增加，点云坐标会相应地改变，平滑后点会出现更多的重合，造成点云数目减少的效果影响模型观测度。图3(c)和图4(c)、图3(d)和图4(d)分别为双边滤波平滑一次和平滑三次的效果图，可以看出虽然双边滤波在一定程度上保持了点云模型的几何特征，但其平滑效果并不明显，且随着迭代次数增加，模型会出现局部失真的情况。图3(e)和图4(e)、图3(f)和图4(f)分别为引导滤波算法平滑一次和平滑三次的效果图，可以看出引导滤波算法能很好地平滑模型表面起伏噪声点，且当迭代次数增加时，模型几何特征保持性能较好，模型点重合数量也较少。

为更好地评价几种滤波算法的平滑效果，定义两个评价标准D和δ。因为几种滤波算法都是对离群点去除后剩余点云的每个点进行处理，可定义D为平滑前后模型点云的平均移动距离。

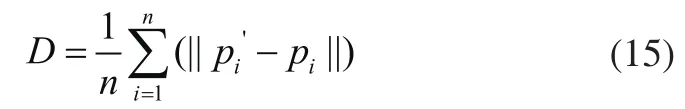
其中，n为处理的点云数量，pi为对应待平滑点；由于此次仿真实验中模型的无噪声标准点云已知，可定义δ为平滑后模型点云的法向量与无噪声标准点云的法向量夹角余弦平均值。

这里，n'i为p'i在平滑后点云模型里的法向量，通过在标准点云中搜索p'i的k邻域，ni为该处法向量。实验计算结果如表1所示。

表1数据结果表明，引导滤波平滑点云模型时，平均移动距离小于均值滤波和双边滤波，从而保证了点云模型不会被过度放大或缩小；平均夹角余弦值δ整体上大于或等于均值滤波和双边滤波对应值，由于δ在(0,π)上是减函数，证明引导滤波平滑后模型整体法向量与标准点云模型整体法向量相比改变较小，即几何特征保持性能更好。

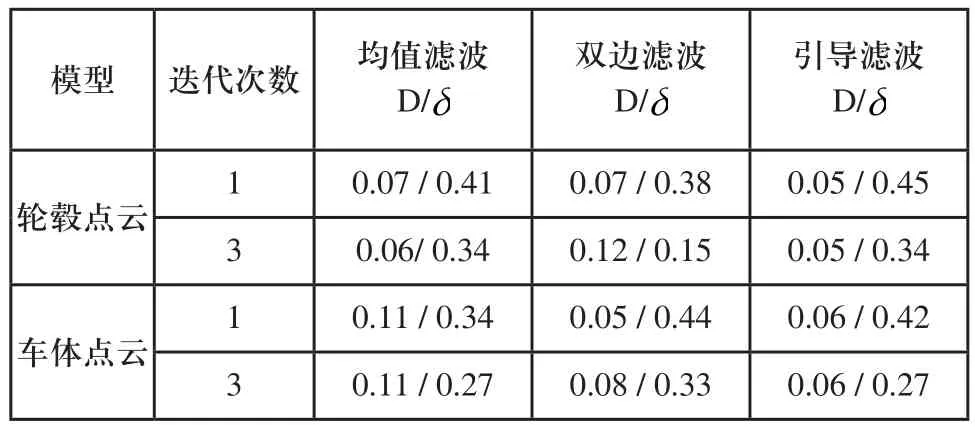
表1 滤波算法评价指标比较

图5 三种滤波算法耗时对比图

图5为算法耗对比图，三种滤波算法对比情况表明，由于引导滤波算法采用局部线性模型，以邻域点集为引导窗口，其算法复杂度低于双边滤波采用的高斯函数加权，高于均值滤波的简单几何中点替代，故点云引导滤波耗时略高于均值滤波，但远低于双边滤波。

4 结论

针对三维信息采集设备得到的点云中含有噪声点，采用高斯统计方法去除离群点，引导滤波算法平滑局部小型噪声点。仿真实验展示了不同参数下高斯统计方法对去除离群点的影响。将点云引导滤波在算法耗时、几何特征保持效果方面分别与线性均值滤波算法和边缘保持特性较好的双边滤波进行了比较，表明引导滤波算法虽然在耗时方面略高于均值滤波，但低于双边滤波一个数量级，且在平滑模型表面噪声点和保持模型几何特征方面效果更好。未来的研究工作重点是，在模型点云稀疏的情况下进行噪声点的去除和平滑。