基于栅格法的机械臂工作空间解析方法研究

张敦凤，赵 皓,2，徐 亮，刘满禄，张 静

（1.西南科技大学 信息工程学院，绵阳 621010；2.中国科学技术大学 自动化系，合肥 230026）

0 引言

在现代工业中，机器人的工作空间是衡量其工作性能的一项重要指标[1]。对机械臂的工作空间的分析研究，有利于分析检验轨迹规划和作业规划的正确性与合理性。许多方法已经提出了在文献中确定机械手的工作空间边界表面[2,3]。其中大部分可分为分析方法或数值方法。分析方法确定封闭形式的描述工作区边界表面，但这些方法通常是复杂的非线性方程和矩阵求逆参与机械手运动学[4]。因此，本文开发设计了一种栅格法的机械臂工作空间解析方法，该方法能够有效克服空间解析计算复杂以及边界奇异点的问题。

1 系统模型建立与工作空间获取

本文建立一个3自由度的机械臂模型，该机械臂第一个关节转轴轴线和第二个、第三个关节转轴不共面且相互垂直。这种结构也满足大多数工业机器人对于一个n自由度的机械臂，可达空间可以表示为各关节变量的正运动学解集：

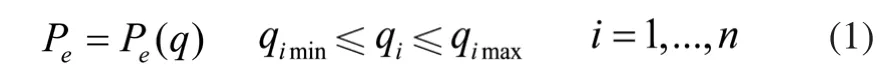
采用蒙特卡洛方法获得3自由度空间[5]。机械臂可达空间的数据点集合为：

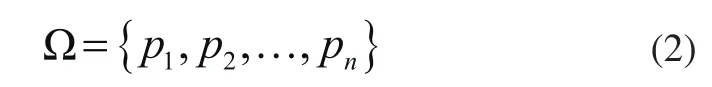
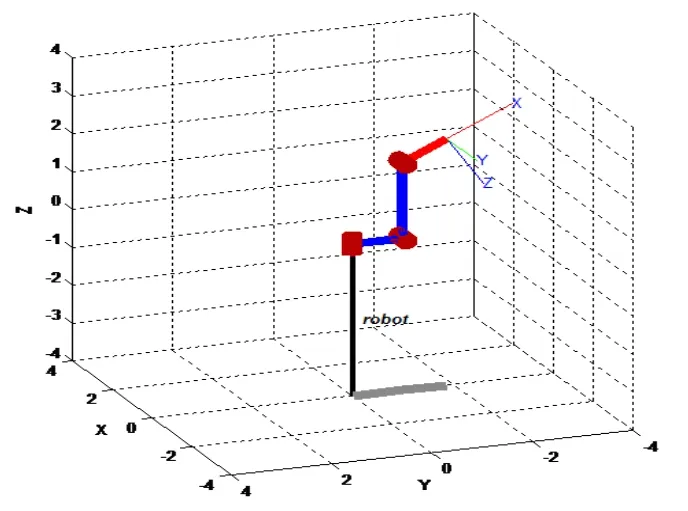
图1 三自由度的机械臂模型

2 工作空间的栅格算法

在极坐标系下边界提取相比在笛卡尔坐标下进行边界提取的计算复杂度要小且可以避开奇异点，具体算法实现步骤：

1）根据机械臂运动学参数建立运动学模型，并运用蒙特卡洛方法求取工作空间。

2）选择基础坐标系的Z轴向，对工作空间进行分层次处理。

3）将每层点云数据取出后，进行极坐标转换，并完成逐层转换。

4）求取边界点并行矢量化处理。

具体算法流程图如图2所示。

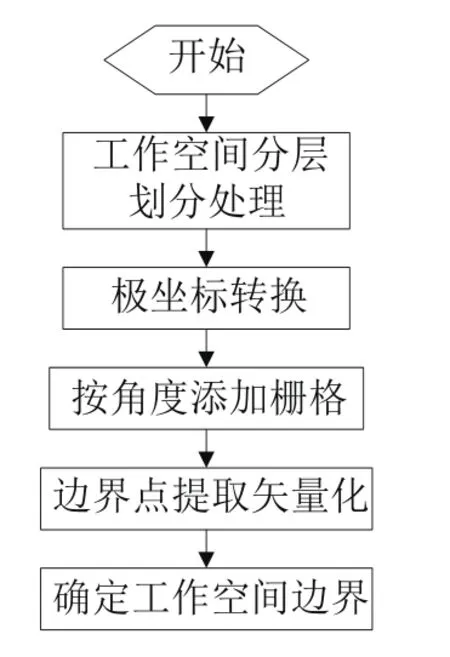
图2 工作空间的栅格算法流程图

3 系统实验与仿真

沿Z轴方对系统建立的工作空间云图分层处理，如图3所示。

图3 工作空间分层图

为了方便数据处理，工作空间分层图在极坐标角度的取值范围均在[0，2π/3]∩[π，2π]区间。本文将可达空间分层图在极坐标系下θ角度的取值范围定义在[-π，2π]区间，以Z=0处切层为例进行笛卡尔坐标系和极坐标系转化，并进行极坐标表示，如图4所示。

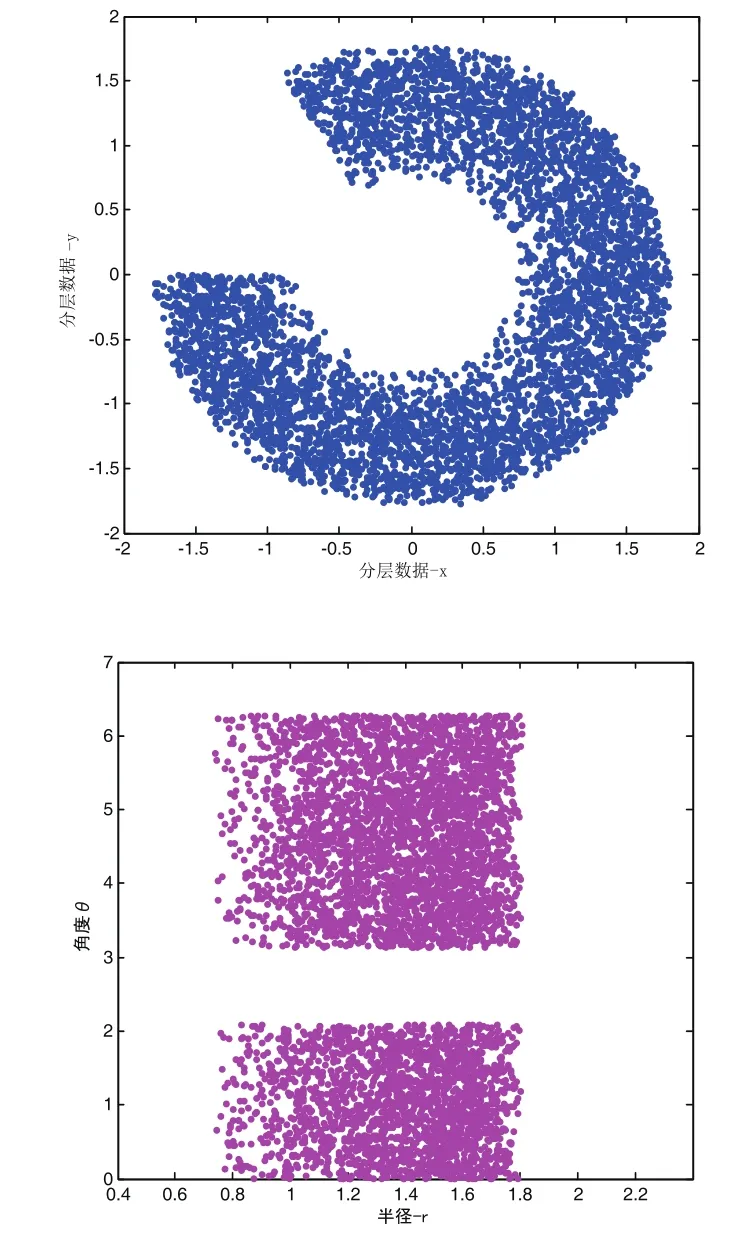
图4 工作空间转换图

在该区间中以每30度为一个区间，分别求解该区间的最值点作为分层图的内外边界点集。

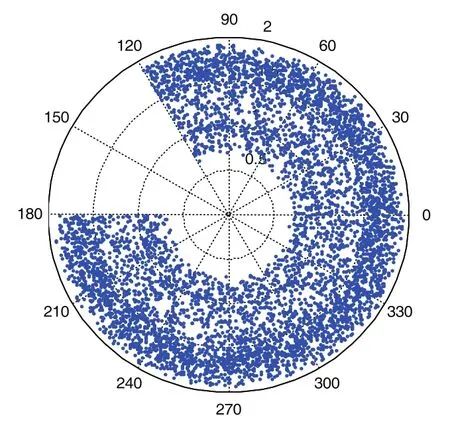
图5 工作空间栅格图

极坐标系下数据做排序分段处理后，利用最值算法式(3)求解出分层数据的内外边界点集，通过点集中数据的标志位找到在笛卡尔坐标系下相应的内外边界点集，栅格图如图5所示，找出极坐标系下分层数据边界点集中的内边界点集发散程度较大点。

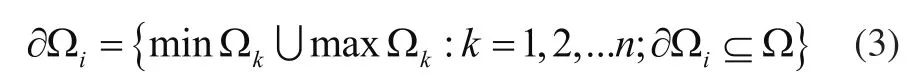
将极坐标系下分层数据边界点发散程度较大点通过矢量化转化为工作空间边界点，如图6所示。在笛卡尔坐标系下，将处理后的单层边界点按Z轴方向叠加可求出机械臂工作空间三维立体边界。

图6 单层工作空间边界图

4 结论

本文重点研究了工业机械臂的工作空间边界解析求解方法。依据工作空间的点云进行分层次分割处理，并通过栅格法求解出工作空间。对于机械臂的工作空间边界解析计算量大，且有奇异点的问题，可有效避免。通过理论分析并进行了模拟验证，该方法求解效果良好，为工业机械臂在实际中应用提供了理论基础。