一种非圆齿轮齿廓离散点快速提取方法研究

林梅彬

（福州职业技术学院 交通工程系，福州 350108）

0 引言

随着齿轮的广泛应用，其齿形的复杂程度也随之增加，如变齿厚齿轮、非圆齿轮、压缩机螺杆转子等。如何简单快速的设计并模拟出切削加工后的精确齿形就显得额外的重要。

在复杂曲面的齿面设计研究方面，吴序堂[1]归纳并提出解析包络法和齿廓法线法两种计算啮合运动共轭曲面的方法，给出了啮合运动共轭曲面的接触条件推算过程；刘朝阳[2]推导了完全共轭理论齿面存在的充分条件，并提出弧齿锥齿轮完全共轭齿面方程的求解方法；林菁[3]提出了一种基于齿面法矢量的直齿雖齿轮齿面曲面求解方法,该方法为直齿雖齿轮齿面的主动设计和三维造型提供了一种新途径；陈兵奎等[4]通过定义曲线与曲面共轭啮合的概念，提出了以适当半径的球体沿啮合曲线的指定等距线包络出管状曲面的齿面构建新方法。然而，根据曲面共轭理论所建立的模型在求解过程中存在两方面问题：一方面复杂的齿面啮合方程求解复杂，另一方面是在发生根切或者双包络时在奇异点附近会出现数值不稳定的现象。因此，一些不需要借助传统复杂的齿面啮合方程即可获得精确齿形的新方法开始被提出，比如借助CAD/CAE软件中的布尔运算方式，完成复杂曲面的三维造型。付自平等利用VB和AutoCAD二次开发实现正交面齿轮插齿加工运动的计算机仿真[5]；迎春等[6]从直齿锥齿轮齿面形成原理出发，提出一种基于SolidWorks三维模型建立方法—边界曲面法；肖莉[7]基于齿轮成形法加工原理，采用Autolisp语言编程对直齿锥齿轮实体进行动态仿真；林超[8]采用范成加工方法，运用SolidWorks设计软件，获得瞬时接触微平面并完成齿廓设计，实现正交复合运动锥齿轮副齿面的精确建模。

本文在虚拟仿真齿轮副共轭成形加工过程的基础上，结合计算机图形学中的图像边缘像素提取相关理论，提出了一种非圆齿轮的齿廓离散数据了提取方法。通过提取非圆齿轮的边缘齿廓，并对齿形误差进行了判定，验证了该方法的精确性和稳定性。

1 非圆齿轮虚拟加工原理

由于非圆齿轮齿面的复杂性，通过一般的啮合方程很难精确获得其齿面。为了能够获得非圆齿轮的精确齿面，由齿轮啮合原理的相关理论可知，非圆齿轮齿面可以通过齿轮刀具与非圆齿轮毛坯做范成运动形成。假设非圆齿轮毛坯固定，刀具与非圆齿轮毛坯在节曲线上作纯滚动。为了获得非圆齿轮的包络齿廓，只需对圆柱齿轮刀具的走刀轨迹进行规划。非圆齿轮包络廓形的精度取决于刀具齿轮的步进角，步进角越小，精度越高。根据齿轮啮合原理和几何运动关系可知，加工刀具与非圆齿轮间的运动关系如图1所示。

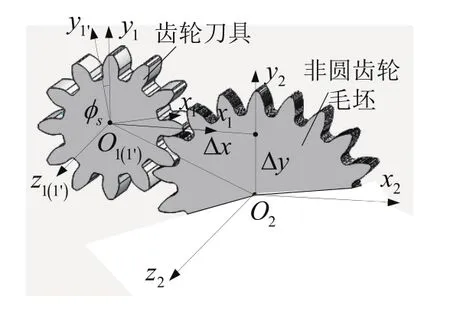
图1 圆柱齿轮与非圆齿轮间的运动关系

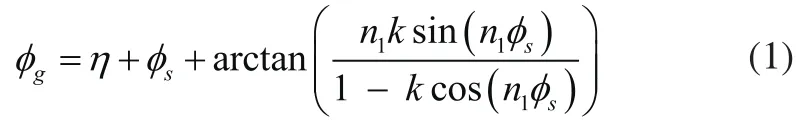
式中，η为圆柱齿轮做纯滚动绕自身轴线角度。

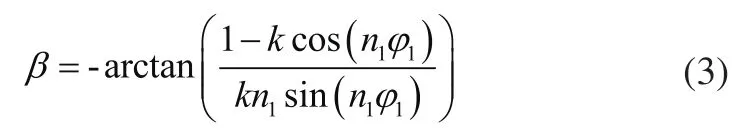
在非圆齿轮的加工过程中，非圆齿轮的齿形取决于加工滚刀的外形及机床的加工误差，以非圆齿轮的滚齿加工为例，由滚刀推导获得的圆柱齿轮的加工包络线方程为：

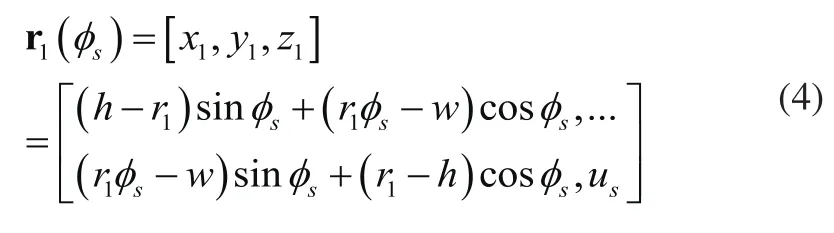
其中h和w分别为滚刀的横坐标与纵坐标。

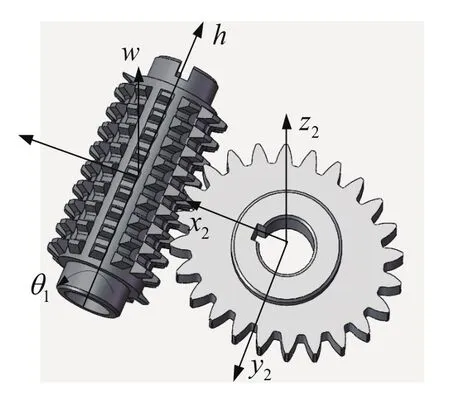
图2 滚刀与非圆齿轮之间相对运动坐标系

则由滚刀和非圆齿轮之间的坐标变换关系可知，非圆齿轮的加工包络线方程为：

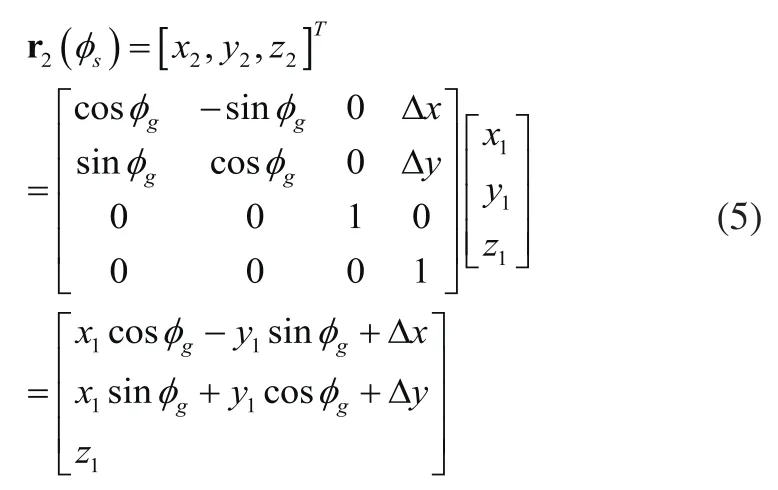
通过以上包络过程可以获得非圆齿轮的包络廓形，如图3所示。

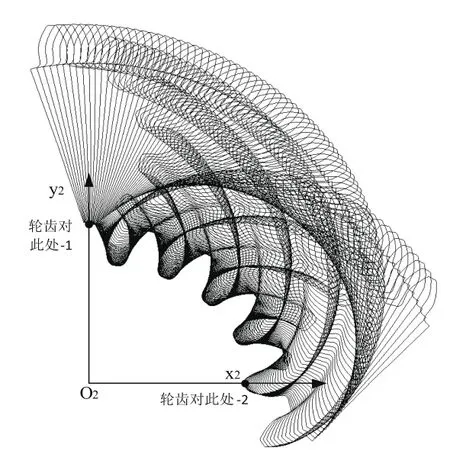
图3 非圆齿轮的包络齿廓

2 图像边缘像素提取方法

在通过模拟非圆齿轮共轭曲面的成形加工过程的基础上，结合机器图形学相关理论，本文提出一种新的齿轮边缘齿廓提取技术。该方法通过定义刀具（可以圆柱形齿轮或者滚刀等）及其走刀路径，在数学软件上获得任意齿廓的包络曲线簇，并将包络曲线簇转化成二值图像。建立矩阵行列与图像像素点坐标相对应的图像二值矩阵，根据不同的轮齿分步旋转图像使每个轮齿关于坐标轴左右对称分布，依次提取每个齿廓的图像边缘像素点，最后利用最小二乘法分段直线拟合像素点坐标，精确得到非圆齿轮轮廓坐标值，具体步骤如下：

步骤1：建立矩阵行列与图像像素点坐标相对应的图像二值矩阵，转化成非圆齿轮齿廓的二值化图像。对于齿轮而言，每个轮齿具有不同的齿廓斜率，由图像的二值化原理可知，不同轮齿得到的齿廓边界像素点的分布规律存在较大的差别，若以此像素点直接作为齿廓离散数据，则不同齿廓间存在较大的误差，如图4所示。

图4 不同轮齿像素点分布规律

为了提高像素精度，结合非圆齿轮的轮齿分布规律，如图3所示，1）非圆齿轮的齿廓均匀的分布在非圆节曲线上，每个轮齿具有一定的差异性；2）为了提高非圆齿轮的受力性能，非圆齿轮的节曲线波谷位置一般加工成左右齿面对称的齿槽。本文考虑通过将非圆齿轮每个轮齿的对称轴转换到图4中的（坐标轴O2y2）图像对称位置，保证每个轮齿都关于对称轴O2y2左右对称，再进行像素点的提取，从而提高齿廓的像素点精度。

步骤2：提取非圆齿轮每个轮齿的图像边缘像素点。在对非圆齿轮齿廓的图像边缘像素点进行提取时，如果直接采用水平或者垂直的扫略方式进行像素点提取，受齿廓的凹凸性影响，则容易造成扫略像素点的缺失，如图5所示。

图5 传统方法的像素缺失

像素点的数量直接决定了齿廓的精度。为了提高像素点的提取数量，结合步骤1中的方法，对非圆齿轮齿廓图像进行转化。

如图6所示，以非圆齿轮旋转中心在图像中的像素坐标P0（x0，y0）建立图像的固定坐标系S2（O2-X2Y2）及回转坐标系S2h（O2h-X2hY2h），假设任意位置轮齿的齿厚中点相对于坐标轴O2y2的回转角为；以轮齿的对称轴建立图像的偏转坐标系S2p（O2p-X2pY2p），定义任意位置轮齿的偏转角为。为了使每个轮齿的对称轴与图像的坐标轴O2y2重合，图像的坐标转换过程包括以下两个步骤：

1）图像中每个轮齿中点P2i绕旋转中点P0回转后，其回转坐标系S2’到固定坐标系S2的齐次转换矩阵为：

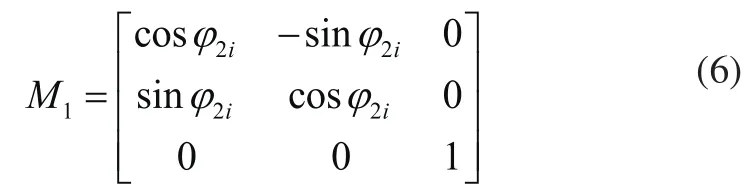
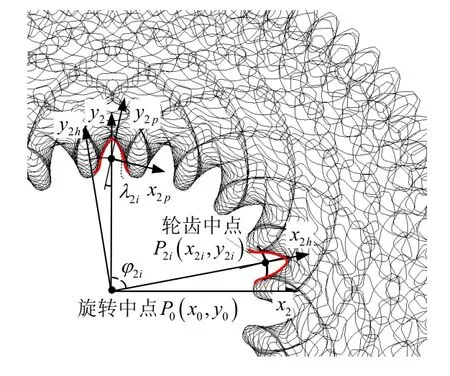
图6 图像像素点的坐标变换过程

由于非圆柱齿轮节曲线不具有高度的对称性，每个轮齿的回转角并不能均匀分布。从齿轮啮合原理的角度上来讲，为了保证齿轮副的正常啮合，必须要保证轮齿均匀的分布在节曲线上，如图7所示。

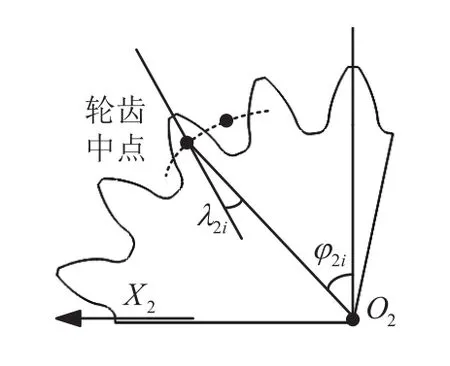
图7 非圆齿轮齿廓分布规律

由齿轮啮合原理可知，相邻两个轮齿中点间对于的弧长为：

则每个轮齿中心相对于坐标轴O2y2的弧长为可以表达成：

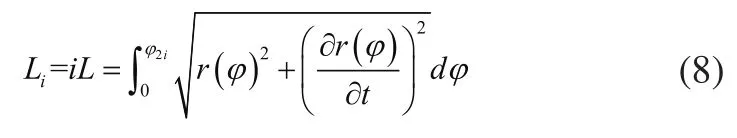
式中，i=1,2,4,……,2z2通过式(8)，即可反求获得每个轮齿在节曲线上的轮齿中点对应的回转角；

2）由于图像回转后只有轮齿中点与坐标轴重合，而轮齿的对称轴仍未与其重合。因此，需要将在图像中将轮齿对称轴以轮齿中心P2i为偏转中心偏转。

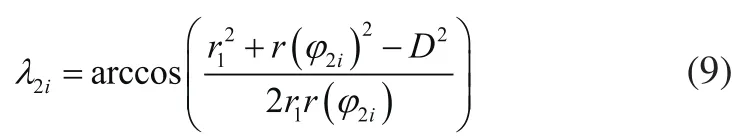
步骤3：通过1）和2）的坐标变换过程，即可得到每个轮齿在二值化图像中关于坐标轴O2y2的对称齿形，再结合水平或者垂直扫描方式，即可获得每个轮齿对于的像素坐标。假设每个轮齿中心在原像素坐标系中的像素坐标点为P2i（x2i，y2i），变换后的坐标点为P2i’（x2i’，y2i’），则两者之间的转化关系为：

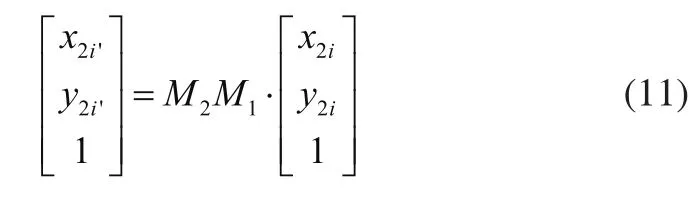
通过以上步骤扫略获得的非圆齿轮齿廓像素点。

步骤4：非圆齿轮齿廓像素点的后期处理。由于提取的像素点与理论坐标之间存在一定的间隔，为了提高齿廓精度，需要对提取的像素点进行后期处理。本文以非圆齿轮中的圆柱孔为标定基准，对非圆齿轮的齿廓像素点进行二次处理，如图8所示。

1）确定非圆齿轮旋转中心在图像中的像素坐标P0（x0，y0），以该点为基准，沿着水平与垂直方向提取非圆齿轮内孔的像素坐标。

2）对像素点进行插值，拟合成圆，并与理论齿廓进行对比，确定两者之间的比例关系，再将提取的非圆齿轮齿廓像素点结合该比例关系获取最终的齿廓像素坐标。

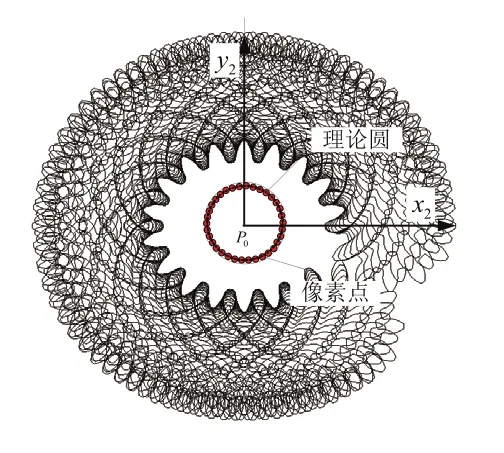
图8 圆柱孔的标定

3 实例分析

本文以直齿非圆齿轮为例进行分析，以验证该方法求解非圆齿轮齿廓的正确性。其中涉及到的基本参数设定如表1所示。

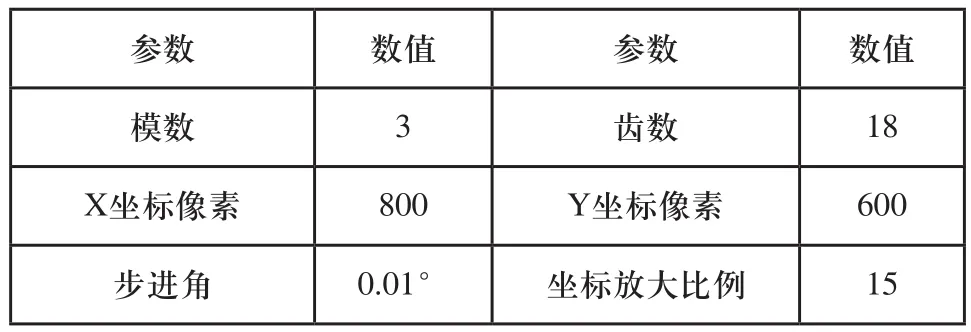
表1 基本参数设定

图9所示为非圆齿轮齿廓对比结果。由图9(a)、图9(b)可知，非圆齿轮的齿廓误差为-7.55～+7.61um，齿廓误差较小，说明通过该方法可精确的获得非圆齿轮的齿廓离散数据点。

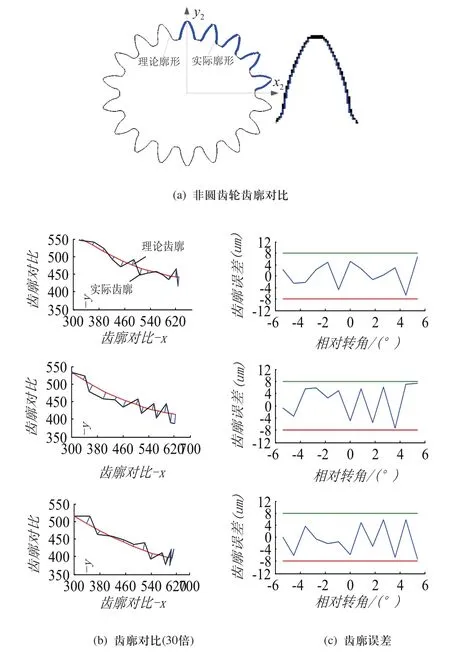
图9 齿廓误差对比

4 结论

本文提出了一种非圆齿轮齿廓的快速提取方法，该方法无需借助复杂的齿轮啮合方程即可完成非圆齿轮齿廓的求解，可应用于求解复杂齿轮的齿廓；该方法运算速度快、数值计算精度高、稳定性好，可直接应用于开发相关的共轭曲面廓形自动生成CAD/CAM软件。